全冠義齒網格過渡算法研究與應用

閆國棟　賈丙輝　林曉華　賈文華　柯廣云

南京工程學院，南京，211167

?

全冠義齒網格過渡算法研究與應用

閆國棟賈丙輝林曉華賈文華柯廣云

南京工程學院，南京，211167

針對全冠義齒數字化設計時外冠和內冠過渡融合的問題，提出了一種新的網格過渡算法。首先提取外冠和內冠網格邊界進行橋接形成封閉孔洞；然后根據定義的三角片插入規則插入新的三角片填充孔洞，構造初始過渡網格；最后投影到由邊界頂點插值得到的隱式曲面上，投影點構成新的過渡網格，將其與外冠和內冠拓撲合并形成完整的全冠義齒修復體。用過渡算法得到的網格面片分布均勻，三角片質量較好，而且過渡邊界光順自然，具有較好的連續性。

全冠義齒；網格過渡算法；隱式曲面；修復體

0　引言

網格過渡也稱為網格融合，是將各個獨立的網格模型融合成一個整體，在游戲創作、藝術造型、三維設計等領域應用比較廣泛[1-2]。在全冠義齒數字化設計中，外冠網格是從數據庫中調用的標準冠模型，內冠網格是組織面向外等距形成的，彼此分離，需要通過網格過渡把外冠和內冠網格連接起來，形成完整的修復體模型才能用于數字化制造。滾動球法是由Choi等[3]提出的參數曲面過渡的經典方法；Liu等[4]將滾動球法擴展到離散網格，通過調節滾動球半徑控制過渡半徑，滾動球法容易實現，但計算效率較低；Ryan[5]提出了一種DRAG-DROP方法，采用拖曳方式把不同模型放在一起，然后采用動態參數化方法實現網格過渡，適用于接觸模型的光滑過渡；林俊聰[6]利用已知網格頂點信息構造隱式曲面，然后采用MC網格化[7]方法將隱式曲面網格化，缺點是構造的三角網格質量較差。從網格質量、魯棒性、效率等方面考慮，現有算法無法滿足全冠義齒外冠和內冠的光滑過渡要求。本文根據網格的拓撲特性，采用橋接方式連接內冠和外冠邊界并進行內生性網格填充，再通過頂點向隱式曲面投影以提升過渡網格的光滑性，較好地解決了全冠義齒網格過渡問題。

1　網格過渡算法

全冠義齒網格過渡要求過渡網格光順自然，特別是過渡邊界要保持相同的連續性，不能有明顯的痕跡，否則既影響美觀，加工時還容易產生應力集中。為此，首先通過網格拓撲結構查詢外冠和內冠模型邊界，采用橋接的方式把邊界連接在一起，形成四邊封閉的孔洞，然后從邊界開始由外向內按照一定的規則插入新的三角片，直至孔洞閉合；這種方式得到的網格屬于C0階連續，在邊界連接處存在明顯痕跡，因此，利用邊界網格頂點和頂點法矢信息插值生成隱式曲面，再通過牛頓法把過渡網格曲面頂點投影到隱式曲面上，得到新的過渡網格，最后更新網格拓撲結構，把它與外冠和內冠網格融合成統一的整體。

1.1邊界橋接

圖1　搭橋網格

1.2網格孔洞填充

網格孔洞填充采用從邊界內生性增長的方式，根據邊界夾角信息按照定義的規則插入新的三角片。定義的三角片插入規則如圖2所示，根據邊界上連續三個頂點構成的夾角大小插入新的網格頂點，圖2a中可直接連接pi-1和pi+1；圖2b中平分∠pi-1pipi+1，長度|piA|=(|pi-1pi|+|pipi+1|)/2；圖2c中把∠pi-1pipi+1三等分，長度|piA|=|piB|=(|pi-1pi|+|pipi+1|)/2；圖2d的情況比較復雜，插入兩個頂點后構成的Δpi-1piA和Δpipi+1B是等邊三角形。

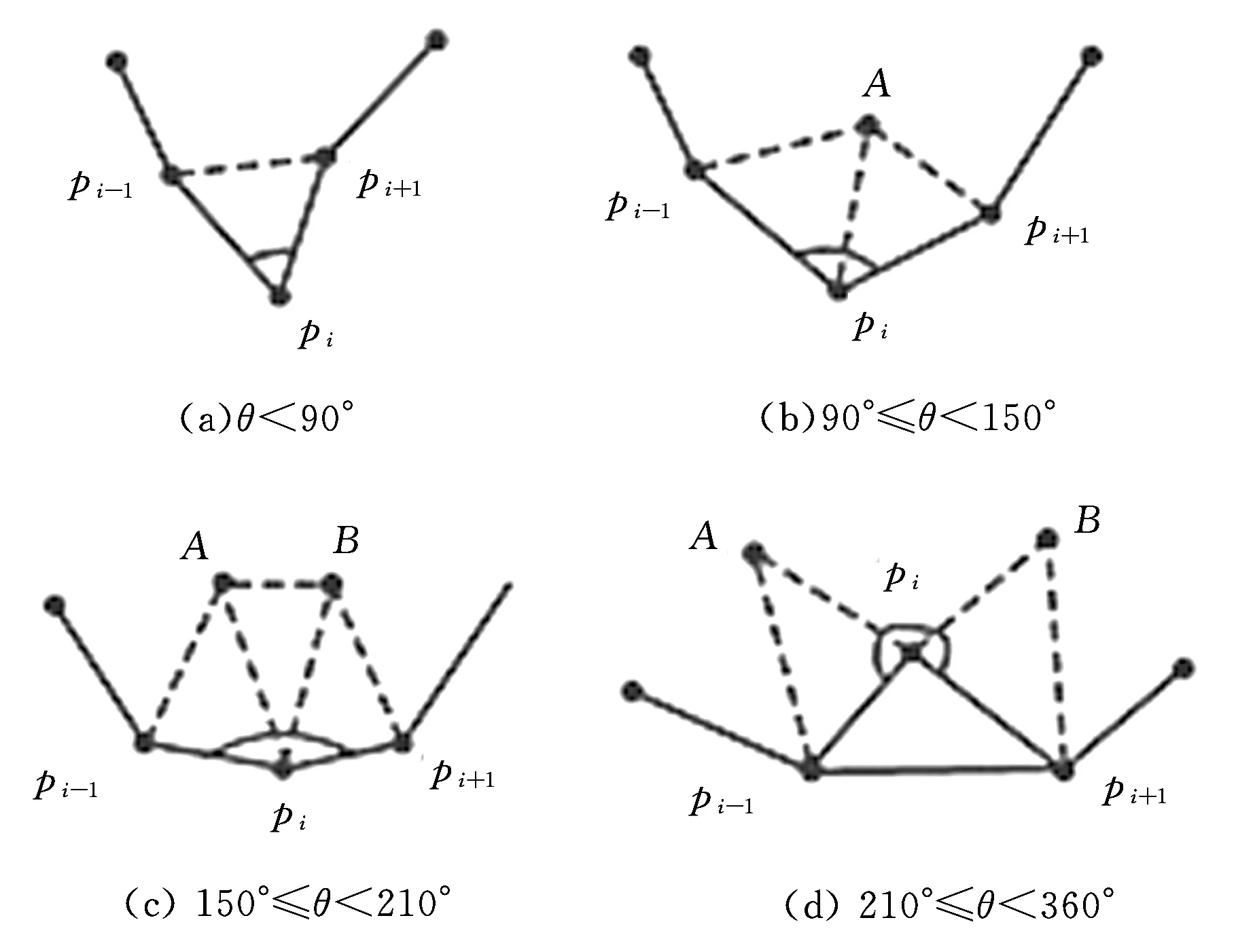
圖2　三角片插入規則

孔洞填充時，首先計算所有邊界夾角的大小并進行排序，取夾角最小的三個頂點根據三角片插入規則構造新的三角片，然后更新邊界信息，刪除已使用的夾角并計算插入三角片與相鄰三角片邊界所構成的夾角大小，取下一個最小夾角繼續插入三角片，直至孔洞完全填充。因為每次都是在最小夾角處插入三角片，所以圖2c、圖2d兩種情況比較少見。需要說明的是，三角片插入過程中，可能出現插入的三角片與原有三角片相交導致網格畸形，所以要進行合法性檢查，張麗艷等[9]在孔洞修補中提出了一種簡便的合法性檢測方法，可避免網格畸形。孔洞完全覆蓋之后，將生成的網格與搭橋網格合并在一起，得到初始過渡網格，因三角片插入過程中未考慮網格光滑性，且過渡網格與外冠和內冠網格連接邊界存在明顯痕跡，所以后續要通過隱式曲面投影優化過渡網格來提升光滑性。

1.3隱式曲面投影

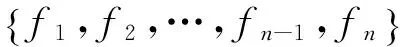
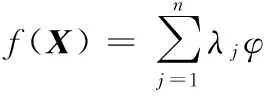
(1)

其中，φ(‖X-Xj‖)是徑向基函數，分為全局支撐和緊支撐，不同基函數對運算復雜度和曲面光滑性影響較大，本文選擇φ(r)=r3作為徑向基。Xj是曲面上給定的約束點，λj表示每個徑向基的權值，p(X)構成了f(X)的線性和常量部分，定義為

p(X)=p0+p1x+p2y+p3z

(2)

為求解權值和多項式系數，要求滿足約束條件：

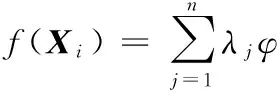
(3)

以及正交條件：

(4)

將各約束點代入式(3)和式(4)，組成線性方程組：

(5)

上式等號左邊矩陣是半正定的，存在唯一解。如果僅選擇曲面上的點代入方程組，每個約束點對應的函數值fi=0，導致方程組只能得到零解，因此，必須增加函數值非零的約束點。實際操作中，以外冠和內冠的邊界頂點作為零值約束點，然后將頂點沿法矢正向和負向各移動0.1單位長度作為非零約束點，利用LU分解[11]可快速求解權值和多項式系數。求出隱式方程后，采用牛頓迭代法[12]將初始過渡網格頂點投影到隱式曲面上，以投影點作為新的過渡網格頂點，得到光滑且邊界連續的過渡網格。

2　算法試驗與分析

圖3所示為利用網格過渡算法進行全冠義齒外冠和內冠融合過渡的過程。圖3a是待過渡的全冠義齒，分別提取外冠和內冠邊界并進行兩次橋接(圖3b)；形成兩個孔洞之后按照定義的三角片插入規則填充孔洞，將填充網格和搭橋網格合并，得到初始過渡網格(圖3c)，圖3c中顯示網格連續性較差。通過邊界頂點構造隱式曲面，將初始過渡網格頂點投影到隱式曲面上，由投影點構成新的過渡網格(圖3d)，光滑性得到明顯提升。更新網格拓撲結構，把外冠、內冠和過渡網格合并在一起，融合成完整的全冠義齒修復體(圖3e)。圖3f所示為合并網格的面片顯示效果，比較過渡區域網格及鄰近網格，可以看出頂點分布比較均勻，三角片形態較好，而且邊界連接處未出現明顯痕跡，說明邊界連續性較好。

圖3　全冠義齒網格過渡

本文算法除了用于全冠義齒網格過渡，還能用于其他模型融合，如圖4所示，將兔首和馬身融合在一起構造異獸模型，這在動漫造型中應用普遍。首先將兔首和馬身放置在合適位置(圖4a)，然后用過渡算法構造過渡網格(圖4b)，更新拓撲將過渡網格與兔首、馬身合并成統一網格(圖4c)，框選處是過渡區域細節放大圖，顯示邊界連續性好且面片繼承了原有網格性質，分布比較均勻。

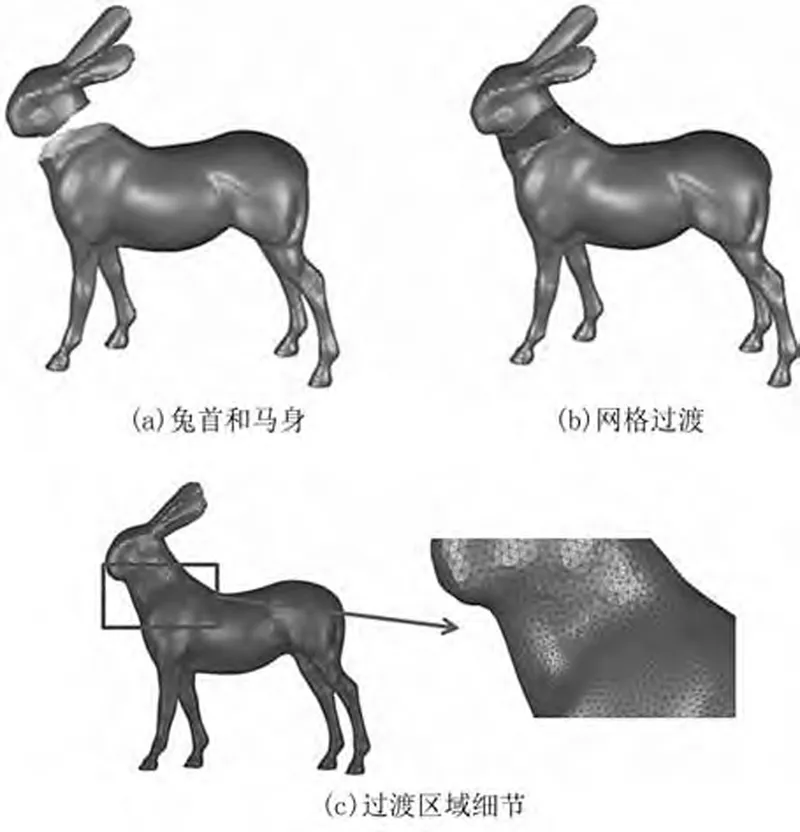
圖4　兔首和馬身網格過渡

圖5a是根據文獻[6]提出的網格過渡算法實現的全冠義齒網格過渡，首先通過邊界頂點構造隱式曲面，然后用MC算法將隱式曲面網格化，再應用網格裁剪、縫合將過渡網格與外冠、內冠合并成統一網格。與圖5b中根據本文算法實現的過渡效果比較，隱式曲面重網格化算法的最大問題是網格面片分布不均勻，存在大量狹長不規則的三角片，網格質量較差，而本文算法生成的過渡網格質量較好。

圖5　算法比較

3　結語

本文針對全冠義齒外冠和內冠網格過渡融合問題，提出了一種新的網格過渡算法，首先通過網格拓撲結構分別查詢外冠和內冠邊界，在邊界之間根據情況進行橋接形成封閉孔洞；然后按照三角片插入規則沿孔洞邊界插入新的三角片填充孔洞，把搭橋網格與填充網格合并，再將初始過渡網格頂點投影到由外冠和內冠邊界頂點插值生成的隱式曲面上，得到頂點分布均勻，內部連續性好且邊界與外冠、內冠邊界光滑過渡的網格。雖然過渡效果總體較好，但是極少數情況下插入的三角片即使經過合法性檢查，仍會出現畸形導致網格填充失敗的問題，如何更好地進行孔洞填充以避免網格畸形是今后研究的重點。

[1]程筱勝,袁天然,戴寧.基于雙向拉鏈的網格模型過渡算法[J].中國機械工程,2009,20(6):693-699.

ChengXiaosheng,YanTianran,DaiNing.MeshBlendingApproachBasedonBi-directionalZipperMethod[J].ChinaMechanicalEngineering,2009,

20(6):693-699.

[2]LeeS,WolbergG,ShinSY.Polymorph:MorphingamongMultipleImages[J].ComputerGraphicsandApplications,IEEE, 1998, 18(1): 58-71.

[3]ChoiBK,JuSY.Constant-radiusBlendinginSur-faceModeling[J].Computer-AidedDesign,1989,21(4): 213-220.

[4]LiuYS,ZhangH,YongJH,etal.MeshBlending[J].TheVisualComputer, 2005, 21(11): 915-927.

[5]RyanS.Part-basedRepresentationandEditingof3DSurfaceModels[D].Toronto:UniversityofTor-onto,2010.

[6]林俊聰.結合隱式曲面的網格融合[D].杭州:浙江大學, 2008.

[7]錢峰, 馬秀麗, 楊勝齊,等.移動立方體算法的研究和改進[J].計算機工程與應用,2010, 46(34):177-180.

QianFeng,MaXiuli,YangShengqi,etal.ResearchandImprovementofMarchingCubesAlgorithm[J].ComputerEngineeringandApplication, 2010, 46(34):177-180.

[8]WangJidong.HalfEdgeDataStructureBasedShortestPathAlgorithm[J].ComputerEngineering&Applications, 2009,45(8):118-120.

[9]張麗艷,周儒榮.三角網格模型孔洞修補算法研究[J].應用科學學報, 2002, 20(3): 221-224.

ZhangLiyan,ZhouRurong.ResearchontheAlgorithmofHoleRepairinginMeshSurfaces[J].JournalofAppliedScience, 2002, 20(3): 221-224.

[10]周元峰.隱式曲面交互造型及其網格化處理問題研究[D].濟南：山東大學, 2009.

[11]徐娟, 姚如貴, 李路,等.優化稀疏LU分解的LDPC編碼算法研究[J].西安電子科技大學學報, 2015, 42(2):127-132.

XuJuan,YaoRugui,LiLu,etal.LDPCEncod-ingAlgorithmBasedonOptimizedSpareLUDecompositioninTheCMMBStandard[J].JournalofXidianUniversity,2015, 42(2):127-132.

[12]YpmaTJ.HistoricalDevelopmentoftheNewton-RaphsonMethod[J].SiamReview, 1995, 37(4):531-551.

(編輯陳勇)

Researches and Applications of Mesh Transition Algorithm for Full-coverage Crown Dentures

Yan GuodongJia BinghuiLin XiaohuaJia WenhuaKe Guangyun

Nanjing Institute of Technology, Nanjing, 211167

For the transition fusion problem of the inner and outer crown in the digital design of full-coverage crown dentures, a new mesh transition algorithm was proposed. First, mesh boundaries of the inner and outer crowns were extracted to form closed holes by bridging. Then holes were filled by triangular facets according to the definition of inserting rules, and the initial transition meshes were structured. Finally, the initial transition meshes were projected onto the implicit surface obtained by the boundary interpolation, and new transition meshes were structured by projection points, which fused the outer and inner crown topology to form a complete full-coverage crown denture restoration. Meshes obtained by mesh transition algorithm distributed equally, and the quality of triangular facets is good. What’s more, transition boundary is smooth, and it has good continuity.

full-coverage crown denture; mesh transition algorithm; implicit surface; restoration

2015-10-16

江蘇省自然科學基金資助項目(BK20131341，BK20150728) ；南京工程學院引進人才基金資助項目(YKJ201302) ；南京工程學院機械學院省級建設學科項目(JXKJ201514)

R783.4; TP391.9

10.3969/j.issn.1004-132X.2016.15.010

閆國棟，男，1986年生。南京工程學院機械學院講師。主要研究方向為計算機圖形學和合金材料切削工藝。發表論文10余篇。賈丙輝，男，1984年生。南京工程學院機械學院講師。林曉華，女，1985年生。南京工程學院機械學院講師。賈文華，女，1982年生。南京工程學院機械學院講師。柯廣云，男，1989年生。南京工程學院機械學院研究生。