遵循認知規律 實施有效策略

張晞

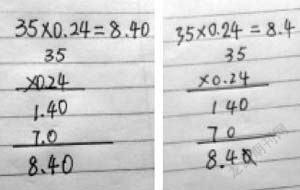
摘要：學生的學習活動非常復雜，教學過程中一定要遵循學生的認知規律，以生為本，順學而教。而數的計算貫穿于整個小學階段，小數乘整數則承前啟后，是在整數乘法基礎上，是小學生學習小數乘法的重要基礎。在教學過程中要立足教材，充分理解教材編者的意圖，同時遵循小學生的認知規律，實施有效的教學策略。

關鍵詞：遵循；認知規律；有效；策略；小數乘整數

“小數乘整數”是蘇教版小學數學教科書五年級上冊的教學內容。其重點是探索并初步掌握小數乘整數的計算方法，會用豎式進行計算。如何讓學生在探索計算方法的過程中，理解小數乘整數的意義，掌握算理、算法，并溝通算理和算法之間的關系，是教學的難點。下面以本課教學為例談一談在計算教學中遵循小學生認知規律的思考與研究。

一、遵循認知規律，找準新知生長點

片斷一：

師：這是明明昨天晚上在超市買的幾種食品。請你選擇其中一種食品的信息，提出一個數學問題。

學生針對四幅圖提出四個求總價的數學問題。

師：同學們提出了這么多問題，怎么解決呢？（板書：四道算式）

師：一起看這四道算式，它們有什么相同之處？

生：都是乘法算式。

師：你能把這四道乘法算式分分類嗎？

師：哪些是我們學過的，一起來計算一下。

師：這兩題是小數乘整數，小數乘整數在生活中的運用非常廣泛，今天我們就在整數乘整數的基礎上來研究“小數乘整數”。

整數乘法的意義和整數乘整數的計算方法是學習這一節課的基礎，是新知的生長點，即是學生自主探究小數乘整數的知識基礎。教師通過創設超市買東西的情境，讓學生從數學的角度自主發現問題和提出問題，組織學生將四道式子分成整數乘整數和小數乘整數兩類，讓學生初步體會小數乘整數的意義和整數乘整數的意義聯系，為新知的探索埋下伏筆。

二、遵循認知規律，自主探究算理算法

片斷二：

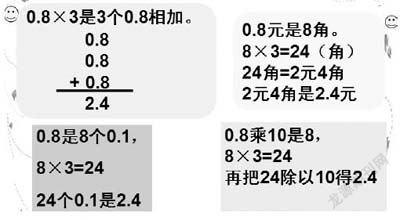
師：我們先看買3根火腿腸多少元的問題，算式是0.8乘3，表示什么意思？

生：表示3個0.8相加的和是多少？

師：根據我們已學過的知識能算出結果嗎？想一想、算一算，把你的思考過程和同桌說一說。

生1：3乘0.8表示3個0.8是多少，所以我用3個0.8相加，得到2.4。

生2：0.8元是8角.3個8角是24角，24角是2.4元。

生3：0.8是8個0.1，8個0.1乘3等于24個0.1，是2.4。

生4：0.8擴大10倍，得到8，再用8乘3等于24。再把24縮小10倍得2.4。

師：比較這三種算法，有什么相同的地方？（指著后面三種方法）同桌相互說一說。

生：三種方法都是把0.8轉化成整數8，然后計算8乘3.最后把算出的整數積化成小數。

師：這幾種算法都是把小數先轉化成整數.借助我們已經學過的整數乘整數的方法算出小數乘整數的積，這個轉化的思路很有價值.我們也可以把這個思路用豎式寫出來。會寫嗎？試一試。

師：我們一起來看這兩個同學寫的豎式，你有什么想說的。

生1：孫潔寫得對，小數點對齊了，張政錯了，他把8和3對齊了，小數點沒對齊。

生2：我覺得張政對的，在家時爸爸已經教過我了。

師：他們兩個都用豎式寫出了0.8乘3的過程，算出了結果。到底誰的對呢？我們來看：這幾種方法都是把0.8看成多少來算？（學生異口同聲：8）

師：根據計算時先算整數8乘整數3.所以數學家們規定把3寫在8的下面，因為計算整數乘整數時我們都是要將末尾對齊。（板書豎式）

師：8乘3的積是24，算完了嗎？

生：沒有，還要加小數點。

師：為什么？小數點加在哪里？相互說一說。

生1：因為8是我們看成8的，實際上是0.8。

生2：因為8表示的是8角，算出的就是24角，現在是多少元？24角等于2.4元，所以要加小數點。

生3：因為8表示8個0.1，所以24也表示24個0.1。

師：同學們很細心，24確實表示24個0.1，也就是2.4.在2的右下角點上小數點。3個0.8元是多少元？（根據學生回答，師板書：8個0.1，24個0.1）

師：請觀察這個豎式，回想剛剛豎式計算的過程，你覺得小數乘整數用豎式可以怎樣計算呢？小組討論一下。

生：小數乘整數，先把小數看成整數，先算整數乘整數的積.再在積里點上小數點。

生：寫豎式要注意整數和整數對齊。

師：你的意思是這兩個乘數的末位要對齊，是嗎？說得真好。

師：剛才同學們用多種方法算出0.8乘3的積，你們真聰明。

學習是個復雜的過程，五年級的學生已有預習的習慣，已經知道0.8乘3的結果，也知道豎式書寫的方法，但不知道為什么這樣寫，也有一部分學生不會預習。基于學生的實際，要讓學生知其然，還要知其所以然，必須在數學學習活動中引發學生的數學思考，鼓勵學生的創造性思維，做到順學而教。因為小數乘整數的意義和整數乘整數的意義相同，所以學生在現實的買西瓜的情境中很容易通過遷移表述出小數乘整數的意義是3個0.8的和是多少？并通過加法經驗得出結果2.4元。下面的三種方法學生也是根據已有的知識經驗將0.8乘3轉化成8乘3，再點上小數點的方法得出結果是2.4元，當學生運用轉化的數學思想理解了算理后告訴學生這些方法也可以用豎式表示出來，實現從算理到算法的飛躍。學生通過自主探究創造出兩種豎式書寫的方法，老師并不急于給出結論，而是讓學生自己辯論，充分經歷知識的形成過程，進一步溝通小數乘整數的算理和算法之間的聯系。小數乘整數的算理和豎式書寫的方法是這節課中學生的兩個思維亮點，值得駐足徜徉。

三、遵循認知規律，借助比較概況算法

片斷三：

師：現在看2.35乘3。現在請大家用剛剛學會的豎式計算的方法動手算一算。指名板演，老師巡視，捕捉錯誤信息。

生：2.35乘3.要先算235乘3得705，也就是235個0.01乘3等于705個0.01，所以積是7.05。

師：算得對不對呢？我們一起用3個2.35相加來驗證一下。

師：同學們，剛才我們列豎式計算了這兩道題的結果.比較一下，你覺得小數乘整數時要注意什么？相互說一說。

生：末尾對齊，按整數乘法算，最后點小數點。

師：對，點小數時我們要想清楚了，不能點錯。

片斷四：

師：我們先按整數乘法算出積，再在積里點上小數點，點小數點時，有沒有簡單的又快又好的方法呢？

生：看因數中有幾位小數，積就有幾位小數。

師：是真的嗎？我們一起來驗證一下。

師：根據他所說的方法說說第一個算式，就舉1，以此類推舉2、舉3。（課件出示：4.76×12，2.8×53，103×0.025，學生判斷積是幾位數）

師：這三題的積是多少？拿出計算器，準備開始。

師：經過剛才計算器的驗證證明了什么？

生：因數中有幾位小數，積就有幾位小數。

師：比如剛才的0.8×3、2.35×3，怎樣給積點小數點？（指著黑板）

生：0.8×3的因數中有一位小數，就從積的右邊起數出一位，點上小數點：2.35×3的因數中有兩位小數，積就有兩位小數.就從積的右邊起數出兩位點上小數點。

師：小數乘整數，怎樣在積里點小數點？自己先說一說，完了再和同桌說一說。

學生已經初步學會小數乘整數的計算方法，在計算2.35乘3時就可以放手讓學生直接計算，乘數是一位數的算法應該是水到渠成的。兩題計算后立即組織學生比較計算方法的相同點，交流概括出小數乘整數的計算方法，實現由具體思維到抽象思維的升華，同時在讓學生通過猜想、驗證自主獲得判斷積的小數位數的簡單方法。這里的每一個細節的地方都留足時間讓學生能深刻思考，符合學生的認知規律，不僅培養了學生的創造性思維，也激發了他們學習數學的興趣。

四、遵循認知規律，深化知識理解

師：我們在購買食品計算總價的過程中，學會了小數乘整數的計算方法，現在我們進行分組比賽，看看哪組同學算得既對又快。

3.7×5=

35×0.24=

0.18×5=

4.6×1.3=

師：（展示0.18×5）咦，前面怎么會有0的？

生：18乘5等于90.因數中一共有兩位小數.就從積的右邊起數出兩位點上小數點，位數不夠的，要寫0占位。

師：（展示35×0.24）看這兩個同學做的題目，你們有什么想說的？

生1：計算的過程中不需要加小數點，要不就變成小數加法了。

生2：乘積是小數，末尾有0應該化簡。

師：小數乘整數到底應該怎樣計算呢？同桌相互說一說。

師：下面我們比一比，快速說出下面小數乘整數的積。

（出示：根據148×23=3404，直接寫出下面各題的積。14.8×23=____，148×2.3=____，148×0.23=____，1.48×23=____。）

師：計算這四題結果的時候有什么相同之處？

生：這些乘法算式，都要先算148×23，然后在積里點上小數點。

師：如果用豎式計算，就要先算什么？小數乘整數先按照整數乘法算.再看因數中有幾位小數就從積的右邊起數出幾位，點上小數點。

學生對于小數乘整數的算理和算法至此都已經理解，這個環節主要是引導學生關注到小數乘整數中容易出現錯誤的地方，一是積的末位0的處理，二是計算過程中加小數點的問題，三是因數中的小數位數的和比整數乘整數的積的位數多，進一步完善小數乘整數的計算方法。特別是計算過程中加小數點只有在乘數是兩位數的情況下才會有學生出現問題，這里一定提供機會讓學生自己發現問題，完善算法，最重要的是讓學生有一個消化吸收的過程，既遵循了學生的認知規律，鞏固了所習得的新知，也體現了面向全體學生的教學理念。