淺析新課程背景下高中數學“三教”教學

羅小林

“三教”教學，即教思考、教體驗、教表達，促進創新型人才的培養。“三教”教學理念是在“高中數學情境問題”教學的基礎上提出的，是“高中數學情境問題”教學的一次升華。那么在教學中，如何通過“三教”來提高高中數學課堂的效率呢？現筆者以自己的教學案例進行分析，以期拋磚引玉。

一、教思考，重在培養學生的思辨能力

教思考，主要指教會學生思考數學中的公理、定理和性質等的來龍去脈，思考數學公式的推導方法，思考具體數學問題的求解方法。

教思考，重在培養學生的思辨能力。在高中數學教學中，教會學生“思考什么”“如何思考”是教學的關鍵。如在教學“拋物線的定義”時，教思考的問題就是：“為什么要尋找平面內到定點的距離等于到定直線（定點不在定直線上）的點？而不是去尋找平面上的定點與定直線的其他位置關系的點？定點在定直線上的動點的軌跡又是什么呢？”

[教學案例1]拋物線的定義

師：居民區內有一口井.其左側有一條從東到西的河流。若我們就生活在這片居民區內，請問我們是到井里取水方便。還是到河里取水方便？

生：找到離井與離河岸一樣遠的那條分界線.分界線外的居民到河里取水方便.分界線內的居民到井里取水方便.分界線上的居民在井里取水與到河里取水一樣方便。

師：你能否畫出這條分界線？

師：（生在大屏幕上用電子筆畫出了這條曲線。）如果我們把井看成一個點.把河流看成一條直線，則剛才的問題變為：“尋找到一個定點與到一條直線的距離相等的動點的軌跡”。那么。大家能否給拋物線下個定義？

生：平面內與一個定點和一條定直線的距離相等的點的軌跡叫做拋物線.

師：很好，但不完整。應如何補充？

生：其中定點不在定直線上。

師：非常好。拋物線的定義是……

“拋物線的定義”教學活動是教思考的典型案例。在這個案例中，通過思考“居民是到井里取水，還是到河里取水”，理解為什么要讓學生思考上面提出的問題，進而理解“拋物線”的涵義。

二、教體驗，重在積淀學生的核心素養

教體驗，即教學生進行學習體驗，體驗教學活動的過程，在“做中學”活動中獲得體驗。

學習體驗包含知識學習的體驗、技能訓練的體驗和思想方法的體驗等。在教學中，知識學習體驗的關鍵，是注重學生對數學知識的學習參與過程；技能訓練體驗的關鍵，是注重學生對訓練技能、訓練技巧等方面的體驗與反思；思想方法體驗的關鍵，是注重對學生進行屬性結合思想、分類討論思想、函數與方程思想、化歸與轉化思想等方面的滲透，培養學生的數學方法。

在教學“隨機事件的概率”時，學生對“用頻率估計概率”這一問題的理解有困難，對頻率與概率理解不透，故教學時教師就注重教學生進行體驗。

[教學案例2]用頻率來估計概率

師：對于給定的隨機事件，可否用事件A發生的頻率fn（A）來估計事件A發生的概率P（A）？

生：可以（但說不出理由）。

師：請各位同學拿出一枚硬幣，在適當高度拋擲一枚硬幣10次，記錄下正面向上的次數，并計算正面向上的頻率。

（大多數學生的頻率為0.3、0.4、0.5、0.6、0.7之一，還有2位學生的頻率為0，有1位學生的頻率為1。）

師：大家以適當高度拋擲一枚硬幣50次呢？

師：請每個小組的5位同學將記錄的正面向上的次數相加，并計算出正面向上的頻率。

（第一組至第十組的頻率分別為：0.492、0.520、0.488、0.540、0.476，0.504、0.568、0.448、0.508、0.484。）

師：請班長統計全班10個小組正面向上的次數和，并計算正面向上的頻率。

班長：0.5028。

師：大家從這些數據中發現這個頻率有何特征？

生：……

“用頻率來估計概率”的教學活動是教體驗的典型案例，通過教學生學習體驗拋擲硬幣的教學活動，計算拋擲硬幣正面向上的頻率，讓學生真正理解“用頻率估計概率”的合理性和有效性。

三、教表達，重在訓練學生的交際能力

教表達，即教學中重視學生的表達、傾聽和交際等方面的能力培養。教表達，其核心是培養學生的表達力，而表達力又分為口頭表達能力和書面表達能力。口頭表達能力是一個人綜合素質的外在體現，是教師教學效果的最直接體現。這需要讓學生參與到教學中，給予學生充分的口頭表達機會，反對教師一言堂；書面表達是教學效果的間接體現，能客觀地將課堂教學中學生存在的問題表達出來。

在教學“函數的單調性”時，學生對“形成增（減）函數的概念”理解有困難，故教學時應注重教學生的表達。

[教學案例3]形成增（減）函數的概念

師：如何描述函數f（x）=x2的圖像在y軸右側是上升的？

生：當x∈（0，+∞）時，y隨x的增大而增大。

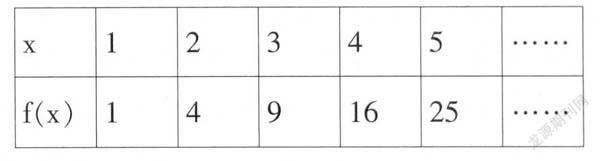
師：觀察如下表格，如何描述表格中數據的變化規律？

生：因為1<2<3<4<5<……所以f（1）

師：如何用數學語言描述y軸右側x與y的變化規律？

生：取兩個數x1，X2，當X1

師：請看反例：2<1，但f（-2）

生：X1、X2∈（0，+∞），當X1

師：很好，如何描述增函數的概念？

生：一般地，對于函數f（x）的定義域為L，如果對于定義域L內的某個區間D上的任意兩個自變量的值X1、X2，當X1

師：很好.大家同理描述減函數的概念吧……

“形成增（減）函數的概念”教學活動是教表達的典型案例，它讓學生學會表達，將自己的想法準確表達出來，真正掌握“增（減）函數的概念”對區間D上任意的兩個自變量都成立。

教思考，重在培養學生的思辨能力；教體驗，重在積淀學生的核心素養；教表達，重在訓練學生的交際能力。只有把這幾方面都不折不扣地貫徹到數學教學中，才能真正落實新課程改革的理念，提高課堂教學的效率。

（編輯 劉澤剛）