基于Petri網的最短路徑算法的研究

段任航，趙佩斯

（桂林電子科技大學 電子工程與自動化學院，廣西 桂林　541004）

基于Petri網的最短路徑算法的研究

段任航，趙佩斯

（桂林電子科技大學 電子工程與自動化學院，廣西 桂林541004）

研究尋找交通最短路徑問題。傳統的最短路徑算法存在計算量大，效率低下等問題。為了更好地求出實時交通狀態下的最短路徑，在先前最短路徑的研究基礎上，提出了基于Petri網的最短路徑搜索算法。該算法可以根據現有的交通路線圖進行建模，再根據實時道路的交通狀況對建模圖進行修改和仿真。在減少計算量的同時，使仿真求出的結果更符合真實的交通狀況。實驗結果證明，新算法和經典Dijkstra算法相比，計算量顯著減小可以明顯提高現實路徑的搜索效率。

Petri網；交通網絡；最短路徑；擴充托肯；變遷權值；實時路況；粘滯因子

近年來，隨著人民生活水平的提高，城市規模的不斷擴大，人們出行的需求也日益增加，交通運輸事業面臨著前所未有的壓力:車輛擁擠嚴重、交通事故頻發、道路環境持續惡化。為解決現實的交通問題，最短路徑的研究日益受到大家的重視。最短路徑研究和現實生活中很多重要事物有著非常密切的關系。例如，城市公交的最短路徑搜索系統，緊急救援的公共安全系統，城市水供、電供及氣供線路的規劃和設計系統等[1]。然而由于各種各樣的技術原因，現有的交通運輸服務體系不能滿足人們的實際出行需求[2]。文中主要結合Petri網的理論知識和建模方式將現實的交通運輸網絡轉換為Petri網表示的有向圖，求出相應的運輸網絡中最短有向路徑及行駛時間。

現有的分析最短路徑的方法可分為兩類，一類是運用圖論去分析問題，比較常見的有：Dijkstra算法、SPFA算法、Floyd算法等；一類是運用網論去分析問題。針對最短路徑算法的研究國內主要有：高明霞[3]為網絡中的各個弧設置了一個距離標號和緊前弧標號，通過不斷迭代，，更新弧的標號來尋找最短路徑。鄭年波[4]將交通路網表達為動態對偶網絡，推導了滿足先進先出特性的動態行程計算方法，設計了時間依賴的標號設定最短路徑算法。唐小勇[5]和杜牧青[6]從數據存儲結構和算法兩方面著手求解最優路徑。

物流配送路徑選擇是典型的離散事件系統，選擇 Petri網對物流配送路徑選擇進行模擬比較合適[7]。文中就是運用一定程度上改進的Petri網方法。文章首先簡單介紹了Petri網的基本原理和概念，然后將現有的路線圖轉化為有向的網絡圖，運用Petri對有向網絡進行分析，最終求得所需的最短路徑。本方法不僅能準確求得最短路徑，而且在實用方面比傳統的方法更為優越。

1　Petri網的交通網絡建模

1.1Petri網概述

Petri網是一種網狀的信息流模型，是一種適合于并發、異步、分布式軟件系統規格與分析的形式化方法，也是一種進行系統分析和模擬的圖形化建模的工具，由表示狀態的元素庫所P（Place）和表示狀態變化的元素變遷T（Transition）[8]兩類元素組成。

其中網的部分描述系統的結構，標識部分表示系統的狀態。通常，小圓圈表示庫所用來決定變遷是否使能，而小方框表示變遷用以改變系統的運行狀態。庫所與庫所之間，變遷與變遷之間不能有依賴關系。

1.2擴充Petri網

本文需要對日常的公共交通運用Petri網進行仿真建模，考慮到如果只用最基本的Petri網難以描述和計算，因此有必要對托肯和變遷的使能規則進行擴展。

首先對Petri網的托肯進行附加描述。平常的Petri網圖中的托肯只有一種狀態，用庫所中的小實心“·”表示。現在再賦予其另外一個描述，用空心“△”表示。該托肯表示該庫所的輸入集合·Pi變遷發生，但車輛尚未駛入該庫所，如圖1所示。

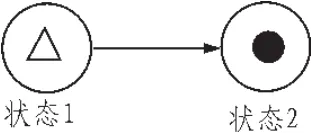
圖1　托肯的狀態變化Fig.1　Token of status change

狀態1表示，該庫所的輸入變遷已經發生，車輛從前一個地點出發，正在趕往該地點的路上，狀態2表示車輛已經到達了庫所。

然后，對變遷規則進行新的定義：

規則1：當庫所Pi處于狀態2時，托肯的運行方向由集合R′i決定。R′i=Ri-（RiI B），其中Ri是符合行駛方向的所有通過變遷與Pi相連接的庫所集合，B是已有托肯進入或通過的庫所集合。

規則2：當庫所Pi處于狀態2時，托肯立即駛出不在庫所停留，表明車輛不會在非目的地停留。

規則3：若庫所Pi的狀態由1變成2，則該庫所的·Pi里面的其余托肯移除網路，說明起點到該庫所的最短路徑已找到，其他到該庫所的路徑舍去。

規則4：當目標點終點庫所的狀態變成2的時候，算法結束，得出所求的最短路徑。

1.3交通運輸網絡的Petri網表示

Petri網是由（S，T；F）決定的二元圖，圖2是一個簡單的路徑圖進行Petri網建模的結果，庫所代表路徑圖的站點，變遷代表節點之間的道路，變遷上的權值代表按標準行駛速度（40 km/h）行駛完該路段所需的時間。下圖是根據現有的路徑圖進行建模的結果，路徑圖上所有站點和路徑信息都完整的顯示在了圖上。

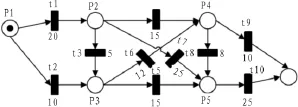
圖2　路徑圖Petri網建模Fig.2　Roadmap Petri net modeling

上圖是由實際的6個站點和10條道路的Petri建模圖，站點抽象的庫所集

P={P1，P2，P3，…P6}，道路抽象為變遷集T={t1，t2，t3，…t10}。變遷上的權值是走完該道路所需的單位時間。變遷的權值集W={w1，w2，w3，…w10}。

1.4實時道路狀態反饋思想

路徑問題不能局限于地理意義上的距離上的最短，理論上距離最短的路徑可能實際上不是最優路徑[9]，所以應將通過所選道路所需的實際時間作為物流調度算法的主要考慮因素。這里將道路的交通狀況作為考慮因素。文中在此提出一個粘滯因子β，β∈[1，+∞）。

我們根據公共交通的現實情況，將默認的車輛行駛標準速度定為40 km/h，則根據實時的交通情況定義如下：

1）通暢：v0≥40 km/h，β=1；

2）輕度擁擠：40 km/h>v0≥30 km/h，β=2；

3）擁擠：30 km/h>v0≥20 km/k，β=4；

4）重度擁堵：20 km/h>v0≥10 km/h，β=8；

5）堵塞：v0<10 km/h，β=∞。

這樣，便可根據實時的道路交通狀況來確定粘滯因子β的值，將得出的值參與到后續計算的考慮之中。下圖在圖2的基礎上通過添加β來還原實際交通狀況。

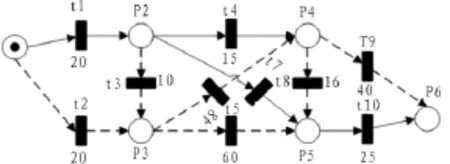
圖3　加入粘滯因子后建模圖Fig.3　After adding sticky factor modeling diagram

上圖可知，根據后加入的粘滯因素β，反饋后的權值集合

從反饋可得知，t2，t3，t5，t6，t8，t9路段道路發生了擁堵和不暢，這樣文中在進行算法研究時可及時避開擁堵路段，為后續工作提供保障。

2　最短路徑Petri網仿真算法

2.1算法原理

該算法將已知的路徑圖進行Petri網建模，用Petri網將復雜的交通路徑用簡潔的方式表示出。再通過1.3節提出的粘滯因子對已有的Petri網模型進行變遷權值的修改，真實還原實際的道路交通狀況。1.2節中的變遷規則避免了一些無意義的查找，保證了算法的計算效率，當目標庫所的狀態變為狀態2時，整個算法結束，得到最短路徑序列。

2.2算法的具體步驟

步驟1：根據路徑圖對其進行Petri建模，其中將路徑圖中的站點抽象為庫所集合，將連接各站點之間的道路抽象為變遷集合，站點之間的距離抽象為變遷上的權值集合；

步驟2：根據1.3節提出的粘滯因素β和前方實時得知的交通情況對建立好的Petri網模型進行相應的變遷權值修改；

步驟3：起始庫所中托肯的狀態變為狀態2，算法開始。起始庫所進入集合B，與起始庫通過變遷相連的庫所托肯狀態變為狀態1；

步驟4：若庫所中托肯狀態從狀態1變成狀態2，則該庫所進入集合B，與之相連的符合規則的輸出變遷集合使能，相應的庫所變成狀態1，開始路途耗時，直到托肯進入相應庫所；

步驟5：處于狀態1的庫所Pi如果∈B，則其輸入變遷集合·Pi不使能，否則正常使能；

步驟6：當目標庫所的托肯狀態變為狀態2時，算法結束，否則回到步驟4直到目標庫所托肯狀態變成2。

如圖4所示為本算法的具體流程圖。

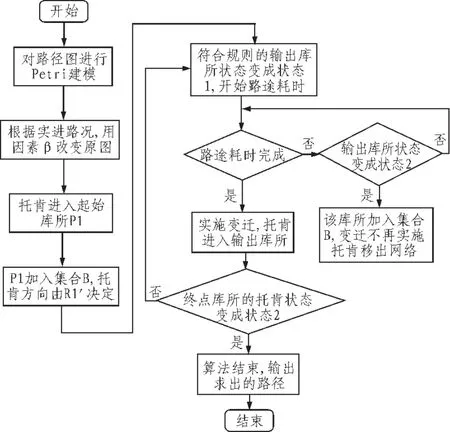
圖4　最短路徑算法流程圖Fig.4Shortest path algorithm flowchart

2.3算法應用實例

圖5是某地方的交通地圖，起點是①，目的地是輥輰訛，線段代表點之間的路，線上的數字代表通過該路段所需的單位時間（按速度40 km/h計算）。本節使用Petri網對其進行建模，并與下節的經典Dijkstra算法求解進行對比，以此來論證算法的可行性、實用性。

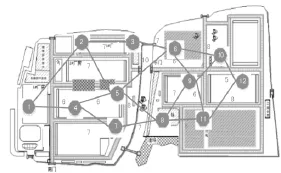
圖5　某地區的交通地圖Fig.5　Traffic map of an area

2.3.1Petri網最短路徑算法

由圖5可知，起始地點是①，目標地點是輥輰訛，則對該圖所建模型如圖6。

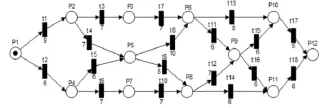
圖6　交通地圖的Petri網表示Fig.6　Traffic map Petri net representation

此時根據前方提供的最新道路狀況得知，從②和③，④和⑤，⑤和⑧之間的道路出現擁堵，其平均速度分別是：22 km/h，20 km/h，26 km/h；①到④，③和⑥，⑥和⑩之間的道路出現輕度擁堵，其平均速度是35 km/h，32 km/h，33 km/h；⑧和輥輯訛，輥輯訛和輥輰訛之間的道路出現重度擁堵，其平均速度是15 km/h，12 km/h，其余路況正常。則文中根據粘滯因素β對建立好的Petri網模型進行相應的變遷權值修改，修改后的圖如下。

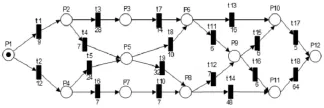
圖7　修改權值后的Petri網圖Fig.7　Right to amend the Petri net value

修改后的權值表示按照現在的交通狀況，走完相應道路所需的單位時間。現在根據2.2節的步驟按步進行算法的仿真，由于篇幅限制，在此只寫出幾個具有代表性的單位時間，對應的其中時刻由圖8所示。

1）時刻0，圖8（a），此時算法開始，集合B=覫，R′1={P2，P4}。如圖8（a），P2和P4的托肯進入狀態1，此時路途耗時開始，P1加入集合B；

2）時刻9，圖8（b），此時庫所P4中的托肯進入狀態2，B= {P1，P2}，R′2={P3，P5}其的輸出變遷t3和t4使能，而庫所P4中的托肯還處于狀態1，路途耗時還有單位時間3；

3）時刻 12，圖8（c），庫所P4中托肯進入狀態2，B={P1，P2，P4}，R′4={P5，P7}其輸出變遷t5和t6使能。此時P3和P5中托肯處與狀態1，路途耗時分別還有單位時間25和5；

4）時刻 16，圖8（d），庫所P5中托肯進入狀態2，B={P1，P2，P4，P5}，R′5={P6，P8}其輸出變遷使能，并且因為此時 P4到 P5路途耗時還未結束，R′4I B={P5}，所以·P5中的變遷t5結束使能。P3和P7的路途耗時分別是單位時間21和3；

5）以此類推，當一個托肯提前完成行程到達指定位置的時候，尚在行程中的托肯結束計算，以此保證不重復運算。圖2.5（e）中時刻26，庫所P8中的托肯進入狀態2，B={P1，P2，P4，P5，P6，P7，P8}，R′8={P9，P11}。此時因為P8∈B，而P5到P8的托肯還在進行路途耗時，所以變遷t9，終止使能。同時P6中的托肯進入狀態2；

6）時刻43，圖8（f），目標庫所中的托肯進入狀態2，此時算法結束，還在路途耗時的相關變遷全部結束，托肯移出網絡，B={P1，P2，P4，P5，P6，P7，P8，P9，P10，P11，P12}，而求得的最短路徑是P1→P2→P5→P6→P9→P10→P12，即求得從地圖①～輥輰訛的最短路徑是①→②→⑤→⑥→⑨→⑩→輥輰訛。需花費43個單位時間到達。

圖8　不同時刻對應的Petri網圖Fig.8　Different times corresponding Petri net

2.3.2經典Dikstra算法

經典Dikstra算法是典型的單源最短路徑算法，用于計算一個節點到其他所有節點的最短路徑。其的主要特點是以起始點為中心向外層層擴展，直到擴展到終點為止[10]。

尋找從①到輥輰訛的最短路徑，各個線段上的權值表明距離值，用Dijkstra算法求最短的路徑表示如下：

定義集合S和集合U，初識狀態下S={①}，U={②，③，④，輥輰訛}。在集合U中找出距離出發點①最近的點，加找出的點加入集合S，再以新加入的點為中間點去尋找離出發點最近的點，周而復始，直到終點輥輰訛加入到集合S，算法停止，輸出最短路徑。

限于篇幅，具體過程略過。最終求得S={①，④，⑤，⑧，輥輯訛，輥輰訛}，所以得出①到輥輰訛的最短路徑是：①→④→⑤→⑧→輥輯訛→輥輰訛。

2.4算法優越性分析

由2.3節可知，運用基于Petri網的算法求得的最短路徑是①→②→⑤→⑥→⑨→⑩→輥輰訛，而通過經典Dikstra算法求得的最短路徑是①→④→⑤→⑧→輥輯訛→輥輰訛。根據實時的交通狀況可知，從②和③，④和⑤，⑤和⑧之間的道路出現擁堵，①到④，③和⑥之間的道路出現輕度擁堵，⑧和輥輯訛，輥輯訛和輥輰訛之間的道路出現重度擁堵。經典Dikstra算法求出的最短路徑，正好經過了出現擁堵和重度擁堵的④和⑤，⑤和⑧，⑧和輥輯訛，輥輯訛和輥輰訛之間的路段（時速30 km/h>v0≥20 km/h和20 km/ h>v0≥10 km/h）。所以，實際應用中極容易導致車輛行駛進入堵塞路段，影響正常的出行計劃。經典Dikstra算法求解的過程中通常需要遍歷所有點，在數據龐大的背景下，計算的效率比較低下。

本文提出的基于Petri網的算法避開了這些路段，且在計算的過程中有選擇性地排除了一些路線，避免了重復運算，可較快地求出最短路徑，更可以避免出現車輛駛入已出現堵塞的道路，造成不必要的損失。

3　結束語

在研究最短路徑問題上，文中提出了基于Petri網的最短路徑算法。其面向的是實時交通網絡，可根據實時的交通狀況，改變建模的圖，還可實現通行過程的動態模擬，找出最優路徑。與經典Dijkstra算法相比，本文提出的算法更簡便，靈活度好且運行效率高。其使能規則的更是有效的降低了通行路網上路徑選擇的復雜度，縮小了搜索范圍，避免了很多無意義的尋找提高了查找效率。在交通日益擁堵的今天，本算法更可以通過實時的交通狀況，提前避開可能出現堵車的路段，具有很強的實際意義。

[1]Fang MeiHong，Liu ShaoHua.The design and realization of the shortest path algorithm based on VC++[J].Urban Geotechnical investigation&surveying，2008（1）:43-46.

[2]YAN Han-Bing，LIU Ying-Chun.A New Algorithm for Finding Shortcut in a City's Road Net Based on GIS Technology[J].Chinese Journal of Computers，2000，23（2）: 211-215.

[3]高明霞，賀國光.考慮交叉口延誤和轉向限制的弧標號最短路徑算法[J].蘭州交通大學學報，2011，30（6）:111-114.

[4]鄭年波，陸鋒，段澄澄.道路轉向延遲的動態對偶圖模型[J].中國圖象圖形學報，2010，15（6）:915-920.

[5]唐小勇，程琳，徐上.考慮轉向延誤最短路徑算法及實現[C].南京:第三屆中國智能交通年會論文集，2007.

[6]杜牧青，程琳.考慮交叉口轉向延誤[J].西南交通大學學報，2010，45（2）:249-254.

[7]羅義學.基于智能Petri網的物流配送路徑優化算法[J].計算機工程與設計，2011，32（7）:2381-2384.

[8]王紅英.基于Petri網的軟件模型驗證[D].上海:華東師范大學，2007.

[9]朱文興，賈磊，丁緒東，等.城市交通網絡中的路徑優化研究[J].山東大學學報:工學版，2005，35（1）:74-77.

[10]李磊，張冰.GMPLS網絡中基于約束的最短路徑優先算法[J].電子科技，2007（2）:42-45，50.

The research of shortest path algorithm based on Petri nets

DUAN Ren-hang，ZHAO Pei-si
（College of Electronic Engineering and Automation，Guilin University of Electronic Technology，Guilin 541004，China）

The research of finding the shortest path of traffic.The traditional shortest path algorithm exists the problem of intensive computationally，low efficiency and other issues.In order to find the shortest path in real-time traffic state better，the paper proposes a shortest path search algorithm based on Petri nets on the basis of the research of the shortest path in the previous study.The algorithm can be modeled based on existing traffic roadmap，then modified and simulated on the modeling diagram according to the real-time road traffic conditions.Experimental results show that compared with the traditional algorithm，the new algorithm significantly reduces the amount of calculation that can improve the efficiency of the search for the path.

Petri nets；traffic；the shortest path；expansion tokens；weight of transition；real-time traffic；impact factor

TN99

A

1674－6236（2016）01-0092-04

2015-02-28稿件編號：201502153

段任航（1989—），男，安徽安慶人，碩士研究生。研究方向：智能系統建模。