基于小波和過程神經網絡的時間序列預測模型
劉修恒,呂 鑫,戚榮志,劉 璇,馬鴻旭
(河海大學計算機與信息學院 江蘇 南京 211100)
基于小波和過程神經網絡的時間序列預測模型
劉修恒,呂鑫,戚榮志,劉璇,馬鴻旭
(河海大學計算機與信息學院 江蘇 南京211100)
提出基于過程神經網絡和自回歸模型的組合預測方案。首先,采用二進正交小波變換對原始時間序列分解和重構,分離出原始序列中的高頻部分和低頻部分;然后對低頻部分構建過程神經網絡模型,對低頻部分采用自回歸模型;最后將兩種模型的預測值疊加,得到原序列的預測值。
小波分解;非平穩時間序列;過程神經網絡;自回歸;預測
在現實生活中,非平穩和非線性的時間序列隨處可見,我們并不清楚動力系統變量是如何相互作用的,也不清楚它們如何支配系統的演化的,但這些變量的時頻性是不相同的。模型的好壞對于動力學系統影響巨大,因為它有著重要的理論意義和很大的應用情景。
現如今,世界各地的專家和學者對時間序列的預測和辨識從不同方面進行研究。對于傳統基于統計學的方法,其方法與結論的性能取決于樣本的數量,然而實際情況中,樣本的數量往往是有限的,這就使得傳統基于統計學的方法無法取得很多的效果。由于強大的函數逼近能力與學習能力,人工神經網絡較多地應用到時間序列預測中,但是因為輸入的同步瞬時性的特點,因此人工神經網絡對于序列中真實存在的時間累積效應難以表達。過程神經網絡,由于其在傳統人工神經網絡的基礎之上增加了一個時間聚合運算算子,因此過程神經網絡可以充分體現序列中的時間累積效應。
如何提取原始序列中的低頻和高頻信息并建立模型和序列中的時間累積效應如何表達是有趨向性均值的非平穩時間序列預測的重要問題。二進正交小波對這種時間序列有著較好的適應性[2,8-9],對低頻的分離作用及有著較好應用能力的過程神經網絡,為了解決這類預測問題,文中提出基于小波變換的過程神經網絡和自回歸的組合預測模型。
1 預測原理及方法
1.1過程神經網絡
過程神經網絡,其在網絡結構上與傳統人工神經網絡類似,時變函數是兩種網絡的區別。由于在傳統神經網絡的基礎上多了時間聚合算子,因此過程神經網絡能充分體現原始序列中實際存在的時間累積效應。
1.1.1過程神經元
聚合、激勵、加權組成了過程神經元,圖1是其結構圖。對于過程神經元來說,其輸入和權皆為時變函數,這就使得其不僅有空間上的聚合,還有對時間的聚合。
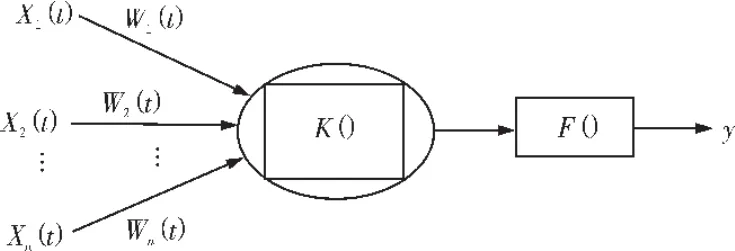
圖1 過程神經元Fig.1 Process neural
1.1.2過程神經網絡拓撲結構
圖2為具有一個隱層的過程神經網絡的結構圖。其中隱層是有過程神經元組成。
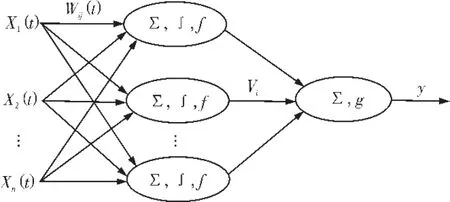
圖2 3層過程神經元網絡Fig.2 Three layer process neural networks
網絡輸出:
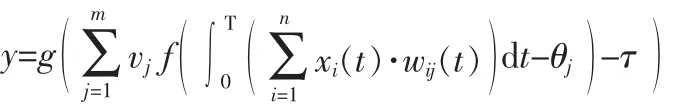
其中,wij(t)是第一層(輸入層)的第i個神經元到第二層(隱層)的第j個神經元的權函數,vj是第二層(隱層)第j個神經元到第三層(輸出層)神經元的連接權,τ、θj分別是輸出層和隱層的閾值,f(·)、g(·)分別是隱層、輸入層的激勵函數,[0,T]為采樣間隔。取,g(x)=x,τ=0,網絡輸出變為

1.1.3時變函數的展開
過程神經網絡權值及輸入皆為時序函數,取正交基函數為{d1(t),d2(t),…,dL(t)},此正交基可以為小波基函數,三角基函數等.將時變函數輸入和權按照一定的精度要求在此選擇的正交基上進行有限展開,得到,,有
則輸出變為
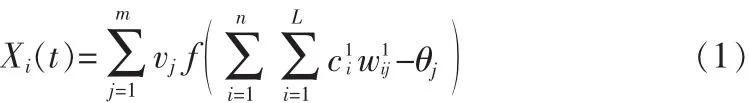

取樣本:X(t)={x1(t),x2(t),…,xn(t),d},則其誤差函數:因此運算得到了簡化,其中參數、vj、θj都是定量值,并且以上參數是輸出y和誤差函數E的自變量。
1.2二進正交小波變換的Mallat算法
1.2.1分解算法
若將設為10原始信號,則由小波變換的Mallat分解算法,有:

其中:G和H分別為高通濾波器和低通濾波器;1j和hj為原始信號在分辨率2-j下的低頻信息和高頻信息;最大的層數為J。最終原始信號分解為h1,h1,h3,…,hJ和1J。
因為該小波分解采用二抽取的形式,使得每次的分解,信號的長度就會減少一半,但是最后的輸出長度和原始信號長度一致,而且信號長度的減少對于預測來說是不精確的,因此需要采用小波重構算法進行重構。
1.2.2重構算法

通過上一步,使得誤差函數公式中的時序變化量沒有了,
其中:H*和G*是對偶算子;j=J-1,J-2,….,0。
對小波Mallat分解后的信號利用式(4)重構采,這樣信號個數可以增加。對h1,h2,h3,…,hJ和1J分別進行重構,得到H1,H2,H3,…,HJ和LJ,有
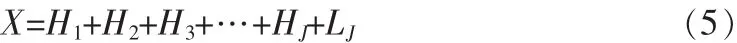
其中:H1:{h1,1,h1,2,…},…,HJ:{h1,1,h1,2,…}為重構高頻信號;LJ:{1J,1,1J,2,…}為重構低頻信號。
1.3基于Mallat算法的PNN-AR預測方法
采用二進正交小波變換對原始時間序列分解和重構,分離出原始序列中的高頻部分和低頻部分;然后對低頻部分構建過程神經網絡模型,對低頻部分采用自回歸模型;最后將兩種模型的預測值疊加,得到原序列的預測值。預測模型框架如圖3所示。

圖3 基于Mallat算法的Process-AR預測框架Fig.3 Process-AR prediction framework based on Mallat algorithm
令Xt:{X1,X2,…}為原始時間序列,對其進行小波Mallat分解以及對各層分解信號進行重構,得到

其中:H1:{h1,1,h1,2,…},…,HN:{hN,1,hN,2,…}為重構高頻信號;LN:{1N,1,1N,2,…}為重構低頻信號。有:
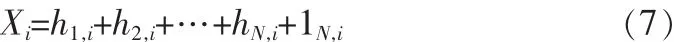
若已知{ti|i≤M}時刻的Xi值,用其來預測k步以后的值,則需要解XM+k,即
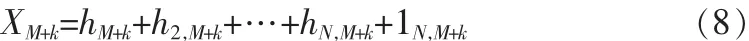
由于H1,H1,H3…HN可近似被當成平穩的時間序列,可分別對其建立 AR(p)模型,并對h1,M+k,h2,M+k,…,hh,M+k進行預測。其預測步驟如下:
1)對Hj建立自回歸模型AR(p),根據已有的h*j,M+k的值對模型的參數進行估計,其中,1≤j≤N,i≤M;
2)檢驗上述模型的適用性;
3)利用適用性最好的AR(p)進行預測,得到hj,M+k的預測值
由于低頻信號LN具有長期趨勢和非線性的特點,可以利用過程神經網絡對低頻信號進行建立預測模型。根據上述過程神經網絡原理,其具體步驟如下:
1)對網絡的層數、各層神經元的個數進行設定,即確定網絡的物理結構;
2)對網絡各層的激勵函數進行確定;
3)根據時間序列數據的特點選擇一個合適的正交基函數θj,1=1,2,…,L,同時設定其個數;
4)根據選定的正交基函數展開所有樣本
5)給網絡參數ε、s=0、θj賦于初始值(i=1,2,…,n;j=1,2,…,m;1=1,2,…,L)
6)對誤差精度ε、最大迭代次數M,累積迭代次數s=0,學習速率初始值η進行指定
7)對所有樣本都按照如下步驟進行操作:
①取樣本集中的樣本1=1,2,…,L,從而可以得到該樣本內元素Li(t),i=1,2,…,n在正交基函數上的展開系數a1i,1= 1,2,…,L;
②利用式(1)、(2)計算輸出y以及誤差函數E的值;
8)當E<ε或s>M時轉9),否則轉7)。
9)輸出學習結果,結束。
2 預測實例
水文數據是一種用于判別和比較預測方法以及具有趨向性特點的非平穩的時間序列,如圖4所示。利用六合水庫的日水位數據來對文中提出的預測模型進行驗證,并將其與單純的過程神經網絡模型比較。首先對原始序列利用db4小波進行2層分解與重構,然后使用PNN-AR(過程神經網絡和AR組合模型)進行預測。利用均方誤差(Relative error)和平均相對誤差(Mean relative error)兩個性能指標來對預測模型的性能進行評價。
六合水庫日水位預測,選取六合水庫1995年之后的共4018條日水位數據來驗證預測模型。原始時間序列如圖4所示。
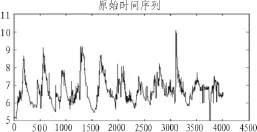
圖4 原始時間序列Fig.4 The original time series
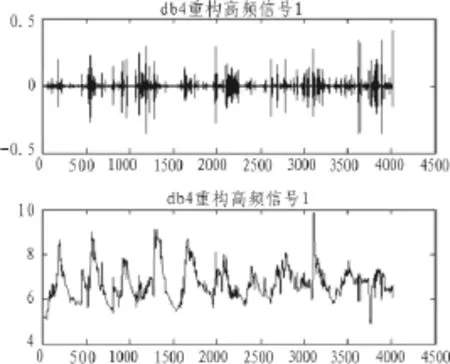
圖5 重構后高頻和低頻信號Fig.5 The reconstructed high frequency and low frequency signal
前3978條水位數據被選取作為訓練數據,后40條水位數據被用作測試數據。PNN-AR模型、過程神經網絡模型以及BP神經網絡模型的預測結果如圖6所示,其中過程神經網絡的網絡結構均為輸入層節點為10,隱層節點為6,輸出節點為1。實驗結果如圖6和表1所示。
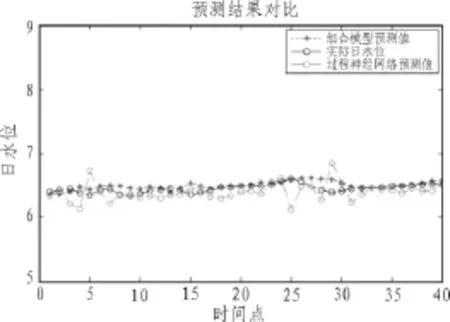
圖6 預測結果對比Fig.6 The results of prediction

表1 誤差對比Tab.1 Error comparison
從圖6和表1可以得出:PNN-AR的預測精度優于過程神經網絡的預測精度,從而說明該方法比單獨使用過程神經網絡泛化能力較強,預測效果較好,能充分擬合低頻和高頻信息。
3 結束語
文中將小波變換[9-11]和過程神經網絡應用于非平穩時間序列的預測。首先根據趨向性非平穩時間序列具有的非線性、波動性和確定性等3個特性,采用二進正交小波變換對原始時間序列分解和重構,分離出原始序列中的高頻部分和低頻部分;然后利用對平穩時間序列具有較好預測能力的統計推斷建模,并結合過程神經網絡,實現對均值具有非平穩特性的時間序列的精確預測。實驗表明,該方法是這類非平穩時間序列的有效預測方法,對進一步解決實際工程問題具有良好的應用前景。
[1]熊沈蜀,周兆英.神經網絡在動力學系統建模中的理論研究[J].清華大學學報:自然科學版,1998(8):26-31.
[2]張坤,郁湧,李彤.基于小波和神經網絡相結合的股票價格模型[J].計算機工程與設計,2009(23):5496-5498.
[3]Zhang G P,Qi M.Neural Network Forecasting for Seasonal and Trend Time Series[J].European J of Operational Research,2005,160(2):501-514.
[4]何新貴,梁久禎.過程神經網絡的若干理論問題[J].中國工程科學,2000,2(12):40-44.
[5]許少華,何新貴.基于函數正交基展開的過程神經網絡學習算法[J].計算機學報,2004,27(5):645-650.
[6]何新貴,許少華.輸入輸出均為時變函數的過程神經網絡及應用[J].軟件學報,2003,14(4):164-169.
[7]許少華,何新貴,李盼池.一類用于連續過程逼近的過程神經元網絡及其應用[J].信息與控制,2004,33(1):116-119.
[8]張晗,王霞.基于小波分解的網絡流量時間序列建模與預測[J].計算機應用研究,2012(8):3134-3136.
[9]李欣.小波變換和模糊凸集投影相結合的圖像復原方法研究[J].電子設計工程,2015(18):182-184.
[10]郜憲錦.基于小波變換的MSK信號碼速率盲估計[J].電子科技,2015(5):140-142.
[11]趙德明.小波變換和曲波變換的圖像邊緣檢測新算法[J].科技創新與應用,2015(13):53.
Time series prediction model based on wavelet and process neural network
LIU Xiu-heng,LV Xin,QI Rong-zhi,LIU Xuan,MA Hong-xu
(College of Computer and Information,Hohai University,Nanjing 211100,China)
A time series prediction method based on AR and process neural network PPN-AR was proposed.By Binary orthogonal wavelet transform,the non-stationary time series were decomposed into a low frequency signal and several high frequency signals.The low frequency was predicted with process neural network,and the high frequency signals were predicted with auto-regression models.The prediction result of the original time series was the superimposition of the respective prediction.
mallat decomposition;non-stationary time series;process neural network;autoregressive;prediction
TN-9
A
1674-6236(2016)01-0009-03
2015-09-10稿件編號:201509079
國家自然科學基金面上項目 (61272543);國家科技支撐計劃 (2013BAB06B04);中國華能集團公司總部科技項目(HNKJ13-H17-04);江蘇省自然科學基金(BK20130852);江蘇省博士后科研資助計劃(1401001C)
劉修恒(1992—),男,安徽阜陽人,碩士研究生。研究方向:數據挖掘。

