城市大規模交通網絡低效路段組合定位及分析
孫黎,凌溪蔓,譚倩,王璞
(中南大學 交通運輸工程學院,湖南 長沙 410000)
?

城市大規模交通網絡低效路段組合定位及分析
孫黎,凌溪蔓,譚倩,王璞
(中南大學 交通運輸工程學院,湖南 長沙 410000)
基于布雷斯悖論現象,根據城市交通網絡中路段或路段組合對路網通行效率的影響,可將其劃分為低效的或必要的,合理關閉路網中的低效路段及路段組合將減少所有出行者的出行時間成本,必要路段及路段組合的關閉將增加出行者額外的出行延誤。采用改進的自適應遺傳算法以有效地定位大規模真實交通網絡中的低效路段組合,結合美國舊金山市大規模實際交通網絡地理信息系統(GIS)數據以及該區居民通勤出行數據進行實證分析。研究結果證實低效路段和必要路段的組合可能是低效的。分析表明,低效路段組合的低效程度|ΔTS|隨著所含路段數量增加呈現先增后減的變化趨勢,含路段數相對少的低效路段組合對路網效率產生更大的影響也更普遍。
城市交通效率;布雷斯悖論;大規模交通網絡;自適應遺傳算法
1968年,德國數學家Braess提出交通網絡中的布雷斯悖論現象[1],即在拓撲結構確定的網絡中,當網絡中的流量分配達到均衡時,增加一條連邊,改變該網絡的拓撲結構,非但不會減少出行者的出行成本,反而增加該網絡中所有用戶的出行成本。該現象為治理城市交通擁擠提供了新的思路。2008年,Youn[2]認為由于出行者總是期望個人出行費用最低,使得系統需要額外損失將近30%的出行成本。1984年,Dafermos等[3]現了道路交通網絡中路段阻抗隨著路網中交通需求改變和路段數量增加而變化的規律。在此基礎上,Pas等[4]的研究發現路網中的布雷斯悖論現象與路阻函數參數取值和交通需求量有關,并提出悖論現象只會在特定的交通需求總量下發生。Hagstrom等[5]分析了布雷斯悖論現象在簡單網絡中的發生機制。直到2010年,Nagurney[6]用數學推導證實在非常大的交通需求下,布雷斯悖論現象隨即消失,并以“群體智慧”解釋了這一現象。Roughgarden[7]的研究表明大規模復雜交通網絡中基于布雷斯悖論研究網絡結構最優化是一類NP難問題,實際上隨著網絡規模的增大,尋求該問題的最優解越難實現。由于大規模實際數據難以獲取,布雷斯悖論的相關研究大多以理論模型為基礎,關于真實數據的仿真分析相對有限。2014年,Bagloee等[8]利用加拿大溫尼伯的路網數據提出了一個利用啟發式算法搜索路網低效路段的計算模型。Sun等[9]研究了大規模實際道路交通網絡低效路段及其屬性特征,提出路網中低效路段的數量和分布與交通流的不均勻分布密切相關。本文作者提出改進的低效路段組合啟發式定位算法,并對低效路段組合屬性進行了深入分析。

1 問題描述
根據布雷斯悖論現象的描述,悖論現象的產生是由于網絡中的納什均衡往往偏離帕累托最優[10],即個體所追求的效益最大化并非系統最優,新增道路看似能為出行者提供便利,卻適得其反。1990年,紐約市決定臨時關閉該市最繁忙路段之一的第42號大街一天,結果該市的車輛通行反而比平時更為順暢。一項調查表明,波士頓的6條公路,曼哈頓的12條公路以及倫敦中部的7條公路如果關閉,或可減少車輛的平均出行時間[11]。由此可見,在特定的交通流下,既有的城市道路交通網絡總是存在一些低效路段,關閉這些路段反而能提高整個網絡的通行效率,減少每個出行者的出行時間。
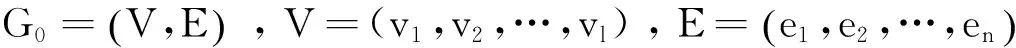
2 定位低效路段及其組合的算法
2.1用戶均衡算法
出行者在路網中總是基于個人出行成本最優選擇出行路徑,此時網絡中所有出行達到納什均衡[12-13]。假設所有出行者對路網都非常熟悉,并選擇從起點到終點之間出行時間最小的徑路,只有當不存在出行者能單方面改變其徑路來降低其行駛時間,出行分布即達到均衡狀態。為計算均衡狀態下各個路段上的車流量fi以及各路段的行駛時間ti(fi),這里采用用戶均衡的Beckmann模型進行求解[14],即出行分布達到均衡時滿足:
(1)
ti由BPR方程求解得出:
(2)
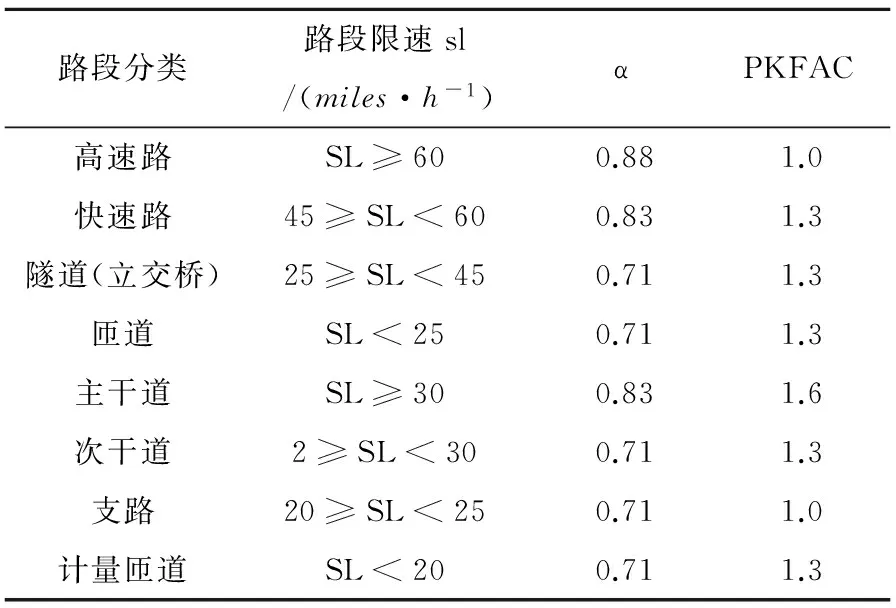
表1 各等級路段PKFAC以及α的取值表[19]
2.2低效路段組合定位算法
近年來,啟發式算法被廣泛應用到路徑優化[20],資源調配[ 21]等組合優化問題中。本文采用改進的自適應遺傳算法定位大規模真實道路交通網絡中的低效路段組合。首先,需要計算初始網絡G0中各路段屬性,具體步驟為:
步驟1:初始化,將既有路網定義為初始狀態G0,求解在滿足用戶均衡的條件下G0中所有出行的出行總時間T,i=1,開始迭代;
步驟2:計算路段ei是否為關鍵路段,如果是,i=i+1繼續步驟2,否則轉入步驟3;
步驟3:在初始狀態中關閉路段ei,得到新路網Gi,求解在滿足用戶均衡狀態下所有出行在路網Gi的出行總時間Ti,并計算ΔTi。若ΔTi<0,則ei為低效路段,否則,ei為必要路段。
步驟4:迭代終止條件:如果滿足i=n則停止迭代;否則i=i+1返回步驟2。
通過以上步驟,可以將G0中的路段劃分為關鍵路段集合Ec,必要路段集合En,以及低效路段集合Ei。以必要路段和低效路段集合組成路段集Et,各路段按ΔTi從小到大排序,并對路段重新編號,編號從1到m,其中m表示Et中的路段總數。Ec中各路段的編號從m+1到n。
其中計算網絡中路段ei是否為關鍵路段的具體方法為:
1)在路網G0中去除路段ei,并利用Dijkstra算法計算所有出行的起點和終點之間的最短路徑。
2)如果出行中存在至少一對起終點之間的最短路徑長度為無窮大,則表明路段ei為關鍵路段。否則路段ei為非關鍵路段。


(3)
算法的具體步驟:
步驟1:計算初始解
從G0的低效路段集合Ei中隨機選擇Q個低效路段構成的初始解集P(0)。其中,每個個體sq只有一個路段處于關閉狀態(且均為低效路段)。t=1,i=1開始迭代。
步驟2:選擇操作

步驟3:交叉操作
對步驟2選擇的兩個父代個體,按照式(4)中的pc進行交叉操作,生成兩個新個體;
(4)
式中:pc1=0.9,Fmax為父代種群中的最大適應度值;Fave為父代種群的平均適應度值;F*為進行交叉的兩個父代個體中較大的適應度值;pc2表示父代種群中具有最大適應度值的個體的交叉概率。
步驟4:變異操作
對步驟3生成的兩個新個體,依據變異概率pm進行變異操作,得到第t代解集P(t)的兩個解st(i)和st(i+1)。
步驟5:收斂性判斷
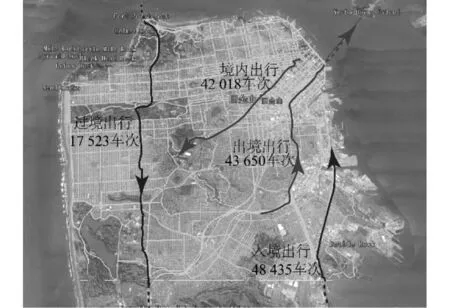
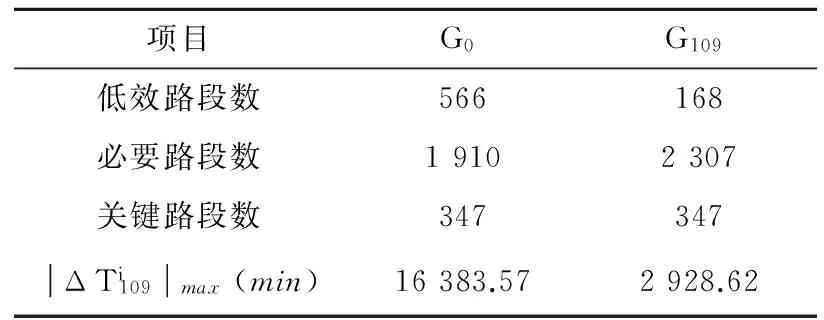
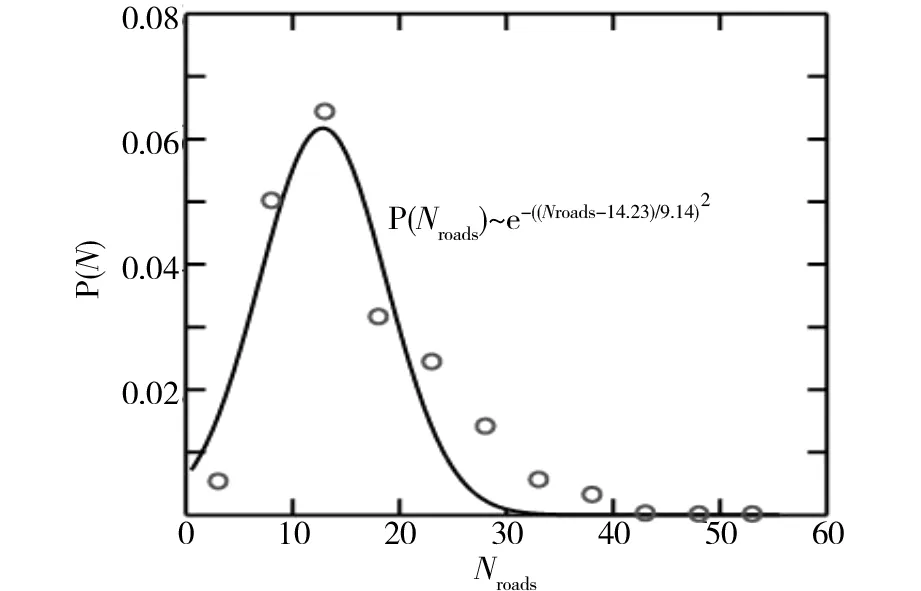
如果i+1=Q且t 3.1舊金山市道路網絡基本信息 圖1 舊金山市地理網絡和出行數據Fig.1 Transport network and traffic in San Francisco 3.2舊金山市道路網絡的低效路段 根據3.1中用戶均衡算法將4.1中舊金山市早高峰小時通勤出行分布到路網G0,得到各路段的車流量fi如圖2所示。 圖2 舊金山市早高峰小時通勤出行流量分布圖Fig.2 Traffic flow distribution of San Francisco during the morning peak 采用3.2中計算路網各路段屬性的步驟,得出舊金山市城市道路交通網絡G0各屬性路段如表2所示。 表2 G0和G109各屬性路段對比 3.3舊金山市道路網絡的低效路段組合 圖3 不同路段數的低效路段組合的|ΔTS|ave以及|ΔTS|max變化曲線Fig.3 Number of roads in inefficient road cluster versus |ΔTS|ave and |ΔTS|max 同時,滿意解集對應的路段組合所含路段數的概率密度分布(圖4)顯示路段組合中Nroads≤20的占比達到75.86%,而Nroads≥40的占比僅為0.3%。整個滿意解集對應的路段組合中Nroads的概率密度呈現高斯分布,擬合函數滿足P(Nroads)=0.068×e-((Nroads-14.23)/9.14)2,其中(R2=0.95)。進一步說明,Nroads相對較小的路段組合在交通網絡中更為普遍,在提高網絡運行效率方面的作用也更大。 圖4 Nroads 的概率密度圖Fig.4 Probability density of Nroads 1)本文實例結果證明,實際道路交通網絡中的一些必要路段和低效路段的組合可能是低效的,低效路段組合的低效程度隨著組合中路段數的增加呈現出先增后減的變化趨勢。 2)低效路段尤其是低效路段組合的研究,對優化交通網絡拓撲結構,提高交通網絡資源利用率,緩解城市擁擠等具有重要應用價值。同時本研究的相關結論可進一步推廣到具有類似拓撲結構特性的復雜網絡系統。 3)需要指出的是:雖然自適應遺傳算法能較快的搜索大量的可行解,但鑒于問題解的規模較大,難以快速定位到最優解,算法的收斂相對較慢。 [1]BraessVD. übereinParadoxonausderVerkehrsplanung[J].Unternehmensforschung, 1968, 12 (1): 258-268. [2]YounH,GastnerMT,JcongH.Priceofanarchyintransportationnetworks:efficiencyandoptimalitycontrol[J].PhysicalReviewLetters, 2008, 101(12): 128701-128704. [3]DafermosS,NagurneyA.Onsometrafficequilibriumtheoryparadoxes[J].TransportationResearchPartB:Methodological, 1984, 18(2): 101-110. [4]PASEI,PRINCIPIOSL.Braess'paradox:Somenewinsights[J].TransportationResearch, 1997, 31 (3-31): 265-276. [5]HagstromJN,AbramsRA.CharacterizingBraess'sparadoxfortrafficnetworks[C]//ProceedingsoftheIEEEConferenceonIntelligentTransportationSystems, 2001: 837-842. [6]NagurneyA.ThenegationoftheBraessparadoxasdemandincreases:Thewisdomofcrowdsintransportationnetworks[J].EPL, 2010, 91(4): 48002-48006. [7]RoughgardenT.OntheseverityofBraess’sParadox:Designingnetworksforselfishusersishard[J].JournalofComputerandSystemSciences, 2006, 72 (5): 922-953. [8]BagloeeSA,CederA,TavanaM,etal.Aheuristicmethodologytotacklethebraessparadoxdetectingproblemtailoredforrealroadnetworks[J].TransportmetricaA:TransportScience, 2014, 10 (5): 437-456. [9]SUNLi,LIULike,XUZhongzhi,etal.Locatinginefficientlinksinalarge-scaletransportnetwork[J].PhysicaA:StatisticalMechanicsanditsApplications, 2015(419): 537-545. [10]WilliamES,RapoportA,DarrylAS.Batchqueueswithchoiceofarrivals:Equilibriumanalysisandexperimentalstudy[J].GamesandEconomicBehavior, 2007, 59 (2): 345-363. [11] 張薇薇. 少即是多, 從布雷斯悖論引出的話題 [J]. 世界科學, 2014(6): 53-55. ZHANGWeiwei.Lessismore,topicslearnfromBraessparadox[J].WorldScientific, 2014(6): 53-55. [12]KubeS,SeltenR,ChmuraT,etal.Commutersroutechoicebehavior[J].GamesandEconomicBehavior, 2007, 58 (2): 394-406. [13]RoughgardenT.Selfishroutingandthepriceofanarchy[M].Cambridge:MITPress, 2005. [14]BeckmannMJ,MeguireCR,WinstenCB.Studiesintheeconomicsoftransportation[M].NewHaven:YaleUniversityPress, 1956. [15]FrankM,WolfeP.Analgorithmforquadraticprogramming[J].NavalResearchLogisticsQuarterly, 1956, 3 (1-2): 95-110. [16] 張歡, 盧毅, 朱東鐵. 基于用戶均衡分析的公路超限車輛補償費率優化模型 [J]. 鐵道科學與工程學報, 2012, 9 (6): 84-89. ZHANGHuan,LUYi,ZHUDongtie.Optimizationmodelonhighwayreimbursementrateofoversizevehicleswithuserequilibriumanalysis[J].JournalofRailwayScienceandEngineering, 2012, 9 (6): 84-89. [17] 史峰, 王英姿, 徐光明, 等. 考慮支路路段雙向車流相互影響的單向交通組織優化 [J]. 鐵道科學與工程學報, 2012, 9(2): 66-71. SHIFeng,WANGYingzi,XUGuangming,etal.Optimizationapproachforone-waytrafficorganizationwithbidirectionalflow’seffectoflocalroad[J].JournalofRailwayScienceandEngineering, 2012, 9(2): 66-71. [18] 周和平, 胡列格, 晏克非. 基于模糊路段流量的OD反推的不確定規劃模型與算法研究[J]. 鐵道科學與工程學報, 2005, 43(1):68-74. ZHOUHeping,HULieke,YANGKefei.Uncertainprogrammingmodelandalgorithmforestimatingorigin-destinationmatricesbasedonfuzzylinkflow[J].JournalofRailwayScienceandEngineering, 2005, 43 (1): 68-74. [19]WilliamAM,NancyAM.Travelestimationtechniquesforurbanplanning(NCHRPReport365) [M].Wasington,DC:NationalAcademyPress, 1998. [20] 胡列格, 夏云, 王佳, 等. 城市公共自行車高峰期需求不均衡的調度優化研究 [J]. 鐵道科學與工程學報, 2015, 12(2): 441-448. HULiege,XIAYun,WANGJia,etal.Schedulingoptimizationresearchondemandimbalanceofurbanpublicbicyclesduringpeakperiod. [J].JournalofRailwayScienceandEngineering, 2015, 12(2): 441-448. [21] 童曉進, 符卓, 劉勇, 等. 連續消耗應急物資調運問題研究 [J]. 鐵道科學與工程學報, 2013, 10 (5): 78-82. TONGXiaojin,FUZhuo,LIUYong,etal.Studyofemergencymaterialdispatchofthecontinuousconsumption[J].JournalofRailwayScienceandEngineering, 2013, 10 (5): 78-82. [22]Navteqoffciolwelsike[DB/OL].http://www.navteq.com/, 2016.7.4. [23]UScensusbareat[DB/OL].http://www.census.gov/geo/www/tiger/tgrshp2010/tgrshp20 10.html, 2016.7.4. Locating and researching of inefficient road clusters in a large-scale transportation network SUN Li, LING Ximan, TAN Qian, WANG Pu (SchoolofTrafficandTransportationEngineering,CentralSouthUniversity,Changsha410000,China) Inthispaper,roadandclusterofroadsintransportationnetworkwereclassifiedasinefficientornecessaryaccordingtotheireffectontheefficiencyoftheroadnetwork,basedonBraess'sparadox.Reasonableclosureofinefficientlinkscanreducetravelcostsconsiderably,whilethefailureofnecessarylinkswouldresultinextratraveldelays.Wemodifiedtheadaptivegeneticalgorithmtopinpointinefficientroadclustersinareallarge-scaletrafficnetwork.Actualtransportationnetworkdatafromgeographicalinformationsystems(GIS)anddailycommutingorigindestinationmatrixintheSanFranciscowereused.Ourempiricalresultsshowthatinefficientroadclustersincludenotonlyinefficientroadbutalsonecessaryroad.Meanwhile,thedegreeofinefficiency|ΔTS|increasesfirstandthendecreasesasthenumberofroadsintheroadclustersincrease.Inefficientroadclusterscontainlessroadwithlarge|ΔTS|,whichismuchmorecommonaswell. efficiencyofurbantraffic;Braess’sparadox;largescaletransportationnetwork;adaptivegeneticalgorithm 2015-11-15 中央高校基本科研業務費專項資金資助項目(2015zzts207) 王璞(1983-),男,河北石家莊人,教授,博士,從事交通運輸規劃與管理、統計物理學、復雜網絡和數據挖掘方面的研究;E-mail:wangpu@csu.edu.cn U491.1+3 A 1672-7029(2016)07-1414-063 舊金山市道路網絡實證分析
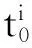

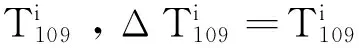


4 結論

