基于MonteCarlo高速鐵路飛砟可靠性分析研究

井國慶，丁東，邵帥

(北京交通大學 土木建筑工程學院，北京 100044)

?

基于MonteCarlo高速鐵路飛砟可靠性分析研究

井國慶，丁東，邵帥

(北京交通大學 土木建筑工程學院，北京 100044)

飛砟現象是影響高速有砟道床應用和發展核心問題之一，飛砟具有隨機性、離散性和復雜性等特點。基于高速鐵路飛砟力學極限狀態方程，綜合考慮飛砟顆粒所處空氣動力流場和道床及其振動不確定性因素，運用MonteCarlo模擬方法對各種不確定性因素進行定量分析，根據飛砟風險可靠度指標，初步對飛砟發生概率進行量化分析和風險評估。研究結果表明，隨著道砟表面平均風速、風荷載負壓力系數和道床振動所致的道砟加速度的增大，飛砟發生概率逐漸增大；隨著道砟質量和道砟顆粒間咬合力增大，飛砟發生概率逐漸降低。飛砟發生概率風荷載影響敏感較強，有必要對高速鐵路有砟道床進行空氣動力學分析，如有砟道床斷面及砟肩選型優化來抑制飛砟現象的發生。

高速鐵路；飛砟；空氣動力；動力作用；可靠度

高速鐵路是從軌道結構形式來看，分為有砟軌道和無砟軌道兩大類，均可滿足300km/h及以上運營。但相較于有砟軌道，無砟軌道由于其本身材料、結構以及鐵道工程運營的特殊性，修復較為困難[1]。另一方面，有砟軌道結構更具有靈活性，易于養護維修、適用范圍廣、建造成本低、速度快等，具有旺盛生命力，尤其是隨著新材料和新結構引入。當然，高速鐵路有砟軌道也存在兩個突出問題，包括：高速鐵路有砟道床劣化及飛砟(遷移)，前者指道床、道砟在反復荷載長期作用下的老化破損現象，主要影響運營耐久性，導致維修周期縮短，維修成本較高；后者指當高速列車通過有砟道床地段瞬間，在高速列車周圍列車風和列車與軌道動力振動共同作用下，表層道砟及車體飛離的冰雪擊打道床表面，進而損害列車裙板、風擋、底盤和鋼軌等軌道零部件上并引起列車和軌道損傷的現象[1]，嚴重影響列車運營安全性與可靠性，如圖1所示。同時飛濺道砟顆粒也會威脅鐵路沿線工作人員安全[4]。

圖1　飛砟危害Fig.1 Ballast flight problem

飛砟問題已有初步研究成果及共識，列車尤其是列車結構、軌道結構、道砟材料與級配、空氣動力學特性、軌道下層基礎特性等均為飛砟影響因素[5-7]。借助現場實測和風洞實驗[6-10]，由于高速列車作用下，有砟道床動力學特性和空氣動力學特性相對復雜，各種影響因素的隨機性較強，因此應用概率可靠度方法，研究列車-軌道動力學、散體力學、空氣動力學等學科交叉帶來不確定性，對飛砟發生概率進行安全性評估，是當前研究熱點和難點。

為此，Francesco[14]提出飛砟風險半量化評估構想，給出了飛砟風險性評定的概念性公式，并分析了飛砟發生的影響因素，包括：風氣候特性、列車荷載動力特性和軌道響應特性。但是該方法仍然停留在定性研究層面，無法給出明確飛砟發生概率，也就無法得到相應失效可靠度。Kwon[11]提出飛砟概率因子定量分析飛砟發生概率，但是僅僅考慮道砟顆粒質量、形狀、列車運行速度等因素，且該飛砟發生概率沒有引入各影響因素概率模型，因此飛砟風險性評估結果有一定局限性。G.saussine[12]采用基于應力-強度干涉理論，建立飛砟概率可靠度模型，但并未考慮道床振動因素。實際上，道床振動對道砟顆粒起始運動具有非常重要的影響，因此忽視這一重要因素不利于對飛砟概率進行更加準確全面分析。

本文基于已有飛砟力學平衡方程，綜合考慮多種飛砟影響因素，包括空氣動力和道床振動等，對飛砟現象進行概率可靠度分析。并通過可靠度敏感性分析計算，將各種不確定性因素影響定量化。本文旨在提出一種飛砟現象風險評估方法，其中所用基礎數據一部分引用國內外已有重要研究成果，并不影響對本文方法的闡述。

1　飛砟可靠度模型

本文的飛砟可靠度分析，主要根據已有飛砟力學平衡方程以及實驗數據，綜合考慮各種飛砟影響因素對其發生概率的影響[2]。根據道砟顆粒受力示意圖，如圖2所示，道床上道砟顆粒在豎直方向上主要受重力mg(m為道砟質量，g為重力加速度)，顆粒間咬合力Fi、荷載Fw(吸力)以及列車通過時因振動加速度導致的力Fa。

根據達朗貝爾原理，得到飛砟極限平衡條件

maT+Fw+Fa=mg+Fi

(1)

其中，aT為道砟顆粒豎向總加速度。將式(1)移項整理，可得

maT=mg+Fi-Fw-Fa

(2)

(3)

式中，a為由于列車動力而引起道床中道砟振動豎向加速度值。為了突出研究重點和簡化計算，本文關注列車空氣動力作用下道砟顆粒豎直向上風壓，根據伯努利流動理論，將此風吸力近似表示為：

(4)

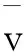
(5)

由此，建立飛砟可靠度功能函數：

(6)

式中：Z為功能函數，當Z=0時，道砟顆粒處于發生遷移、飛濺的臨界狀態。若Z<0則表明道砟處于飛砟狀態，即列車高速運行時形成空氣負壓，引起道砟飛濺的情況；若Z>0則表明處于穩定狀態。

圖2　道砟受力分析Fig.2 Force of ballast particle

2　飛砟可靠度計算

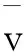
(7)

考慮到飛砟可靠性計算精度要求及極限狀態方程非線性程度，現有一次二階矩方法并不適用，本文擬采用MonteCarlo模擬的方法，解決上述問題，通過借鑒現有知名實驗數據，獲得上述各參數的概率分布類型和統計參數，利用計算機隨機模擬產生具有相同統計特性的隨機數，然后代入到功能函數式(6)中，從而得到功能函數的一個隨機數，重復模擬N次，產生N個功能函數的隨機數據，如果隨機數中有M個數值小于0，根據大數定律，當N的數值足夠大，頻率可視為概率，則飛砟的發生概率：

(8)

根據上述分析過程，利用飛砟力學功能函數和可靠度理論，對飛砟風險概率進行評估，分為如圖所示4步。

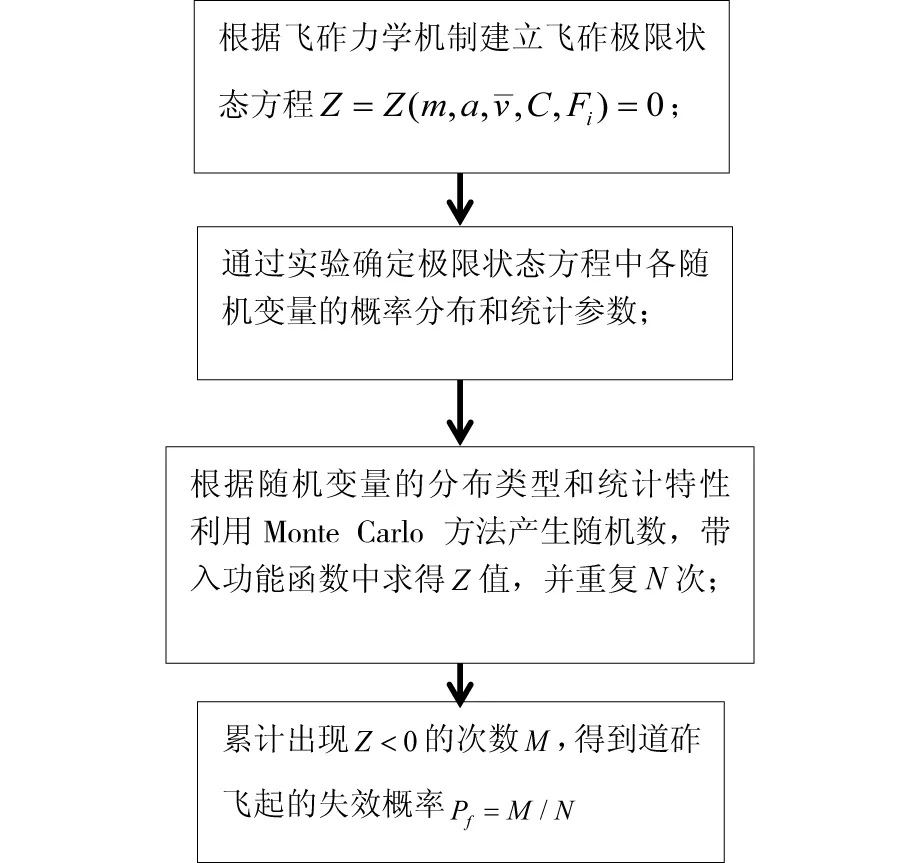
圖3　飛砟概率計算流程Fig.3 Ballast flight probability calculation process

3　參數確定與分析

為研究飛砟發生初始臨近條件和相關影響因素，伯明翰大學在英吉利海峽隧道線靠近梅德斯通的直線段進行現場試驗，列車以最大速度300km/h通過，測量了道床風速、壓力以及軌枕、道砟顆粒振動速度、加速度等物理指標，綜合分析道砟所受動力、空氣動力特性[4]。本文將借鑒其中的一部分數據，來闡明飛砟可靠性評估的研究過程。

3.1參數分析

3.1.1道砟質量

根據以往經驗可知，道砟顆粒質量服從正態分布，可以通過道砟粒徑、級配和道砟密度計算道砟顆粒質量分布。飛砟力學平衡方程中道砟重力指是單顆道砟重力W，其中

W=mg=ρbVg=ρbgV=γbV

(9)

鐵路道砟采用開山碎石破碎、篩分而成，顆粒表面全部為破碎面。不同等級碎石道砟材質的強度和穩定性能中一般都要滿足密度大于2.55g/cm3。其中花崗巖的密度為2.79～3.07g/cm3，特級碎石道砟粒徑級配應符合表1規定。由特級碎石道砟粒徑級配可知，碎石通過方孔篩孔質量百分率分別符合一個范圍，因此取過篩質量百分率范圍中間值，同時求得過篩質量關于粒徑范圍概率密度。如表2所示。

表1　特級碎石道砟粒徑級配

表2特級道砟粒徑過篩質量百分率及概率密度

Table2Sievedextraballastparticlesmasspercentageandprobabilitydensity

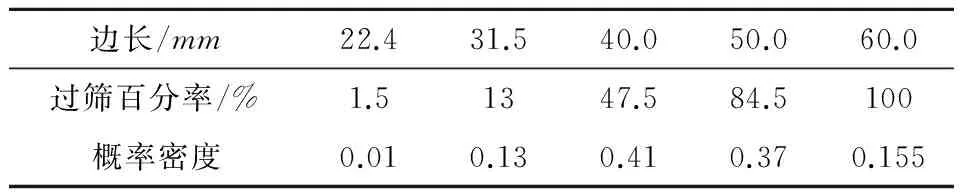
邊長/mm22.431.540.050.060.0過篩百分率/%1.51347.584.5100概率密度0.010.130.410.370.155

由于道砟顆粒通過方孔篩時，道砟形狀又不規則，假設道砟形狀為立方體，則：

W=ρVg=ρD3g

(10)

因D服從正態分布，W也近似服從正態分布。又因ρ的取值范圍為2.79～3.07g/cm3，取其平均值，令ρ=2.93g/cm3。g取9.8N/kg。整理數據如表3所示：

表3　道砟顆粒重力關于直徑的關系

根據表3中各重力值及其概率密度值，有正態分布公式擬合，得到道砟質量的均值

μw=0.31 kg，均方根σw=0.17。

3.1.2骨料咬合力

道砟咬合力主要表現為道砟顆粒之間相互摩擦，與道砟顆粒質量、道床密實度、道砟表面粗糙度等直接相關，道砟咬合力是道床阻力細觀表現形式。由于道砟顆粒質量(重力)關系，道砟咬合力因素基本上滿足標準正態分布規律，但是目前并沒有具體測試數據。在概率分析計算過程中，不妨以該道砟質量(重力)分數代表咬合力因素，作為可以連續變化任意值。比如在分析中假定咬合力為0.1g，然后對飛砟概率進行估測。

3.1.3振動加速度

AndrewQuinn對列車底部的空氣動力學特性(氣流速度、風壓分布)和振動力學特性(軌枕、道砟顆粒加速度、速度)進行測試和分析研究[4]。現場高速列車類型都是Class373或者TGV-TMST，以最大速度300km/h通過。通過布置在道砟顆粒上加速度傳感器，記錄列車通過時道砟顆粒加速度變化數據利用正態分布擬合，如圖4所示，求得道砟振動加速度的均值μa=0.56 m/s2，均方根σa=0.39。需要注明的是，該道砟加速度主要是道床內部加速度值，實際道砟顆粒表面加速度可達到1g甚至以上[2]。

圖4　道砟加速度分布擬合對比Fig.4 Distribution and fitting of ballast acceleration

3.1.4平均風速與風壓系數

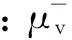
(a)平均風速分布擬合；(b)負向壓力系數分布擬合圖5　平均風速、負向壓力系數分布擬合對比Fig.5 Comparison between distribution and fitting of mean wind velocity and wind pressure coefficients

3.2Monte Carlo分析

根據上面各節所述計算方法與統計特性，匯總如表4所示，通過直接MonteCarlo抽樣的模擬方法，隨機模擬106次，其中有126 108次模擬發生飛砟現象，由此得到上述極限平衡條件下飛砟發生概率為12.6%。至此本文已經根據飛砟的力學機制兼顧各個飛砟影響因素分布特性、統計特性，利用MonteCarlo模擬方法定量分析了飛砟風險可靠度。

同時，為分析飛砟影響因素對飛砟發生概率影響，通過各個因素均值和變異系數取值，分別得到飛砟發生概率與道砟質量、道砟振動加速度、骨料咬合力、平均風速與負壓力系數均值等關系曲線。

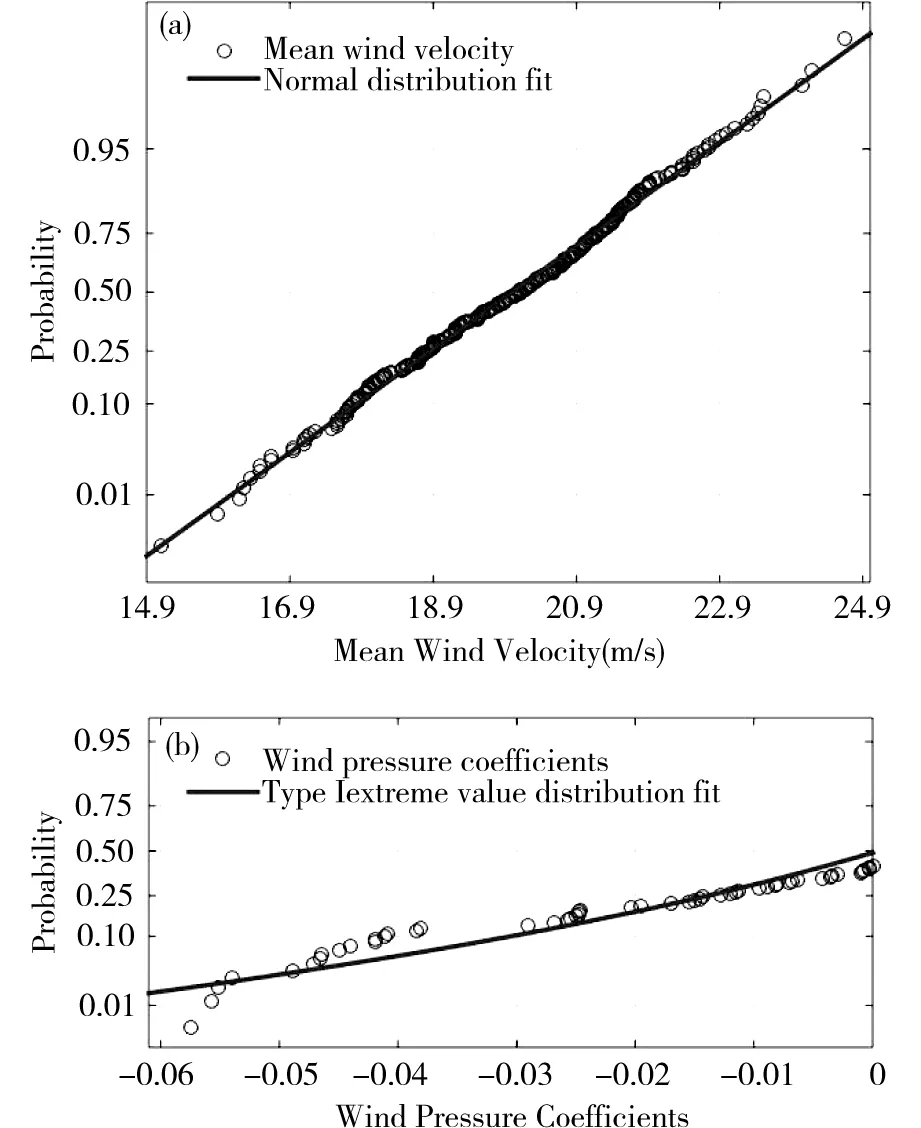
圖6表明，隨著道砟平均質量增大，飛砟發生概率逐漸降低。當道砟質量較小時，增加道砟質量，飛砟概率降低比較顯著。因此高速鐵路有砟道床可通過控制道床表面道砟粒徑、密度材質等方面進行飛砟防治，如合福高鐵巢湖東站區間，將道床表面直徑小于30mm道砟或厚度不足10mm、直徑小于40mm片狀道砟撿拾、清除，將粗顆粒道砟置于道床表面[3]。

表4　飛砟影響因素統計參數匯總

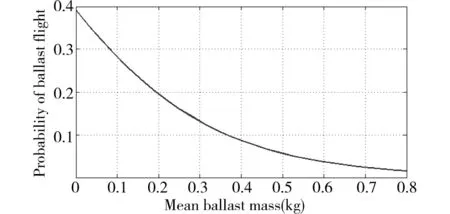
圖6　道砟質量與飛砟發生概率關系Fig.6 Relationship of mean ballast mass and probability of ballast flight

關于道砟咬合力，本文將其簡化為道砟質量正比關系，因此該因素相當于等效為道砟重量，由圖8可見，其變化規律與道砟質量對飛砟發生概率的基本相似。工程應用上，可通過采取對道床進行全斷面夯拍，保持密實、飽滿狀態，提高道砟咬合力[1]。

圖7　咬合力與飛砟發生概率關系Fig.7 Relationship of ballast particle interlock force and probability of ballast flight

平均風速與飛砟關系如圖8所示，當平均風速增大時，道砟所承受向上動力也逐漸增大，此時飛砟發生概率明顯增加。但是當其增大到一定程度以后，飛砟發生概率增減變緩，甚至接近不變。這是由于當平均風速均值增大到一定程度后，如果仍按照低風速時變異系數考慮，再用正態分布擬合，計算會存在一定誤差，會導致風荷載取值和實際偏小。

工程實踐上，可通過列車線形優化、可通過有砟道床斷面及砟肩形式選型來降低道床表面平均風速，進而抑制飛砟發生風險。如合福高鐵巢湖東站區間采用砟肩與軌枕頂面平齊(無砟肩堆高)，在聯調聯試(最高速度328km/h)和運營期間未發生飛砟現象[3]。法國、西班牙采取平肩式道床結構無飛砟發生，意大利早期采用砟肩堆高形式，導致飛砟發生，改為平肩式后飛砟幾率顯著降低[1]。

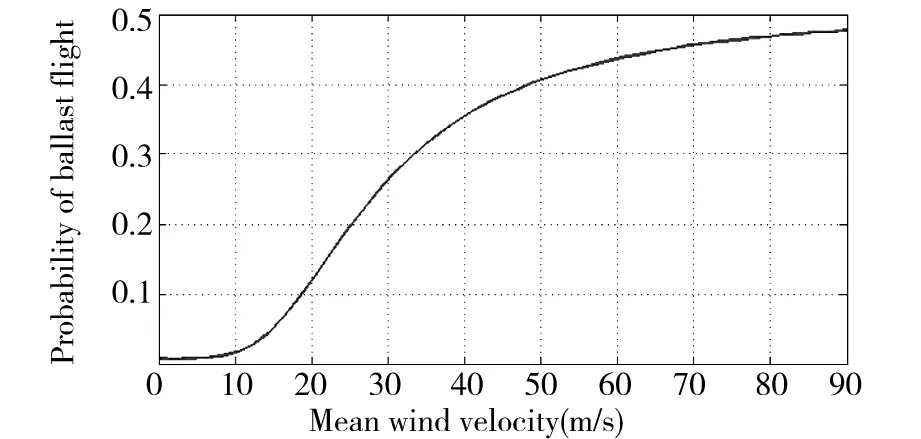
圖8　平均風速與飛砟發生概率關系Fig.8 Relationship of mean wind velocity and probability of ballast flight

風壓系數與飛砟發生概率關系曲線可由圖9看出，飛砟發生概率對風荷載負壓力系數變化敏感。

工程實踐上，道砟顆粒形狀、道床表面平順、軌枕形狀會影響道床表面的流場特性，影響風荷載負壓力系數。可采取空氣動力學優化軌枕、平順道床表面等措施，降低飛砟發生幾率。

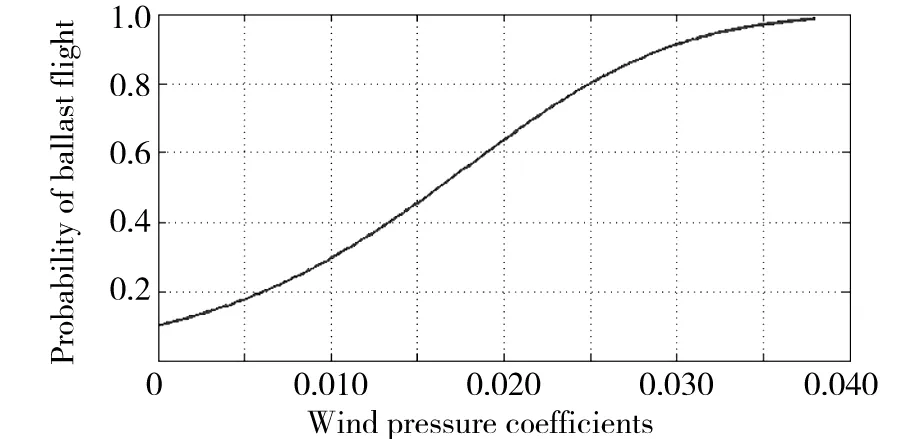
圖9　風壓系數與飛砟發生概率關系Fig.9 Relationship of wind pressure coefficients and probability of ballast flight

圖10可知，道床振動加速度增大導致飛砟發生概率相應變大。低速或者振動較小時，對飛砟幾率影響較小，但高速鐵路情況下，振動加速度較大，如列車速度超過300km/h時，道床振動加速度一般在1g左右，隨著列車速度(振動加速度)繼續增加，飛砟幾率顯著增加。因此高速鐵路可通過優化軌道結構，降低軌道動力效應等方法防治飛砟，如采用高彈扣件、墊板，增大軌枕質量和底部接觸面積等方法，降低道床結構振動特性。

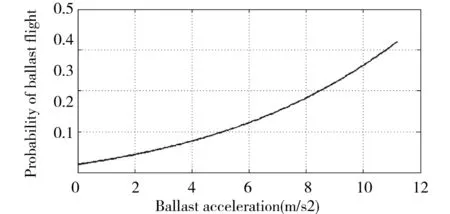
圖10　道砟振動加速度與飛砟發生概率關系Fig.10 Relationship of ballast acceleration and probability of ballast flight

4　結論

1)MonteCarlo方法可進行飛砟可靠度量化分析，有助于將飛砟可靠度從定性研究轉變為到定量研究。

2)道床表面道砟顆粒質量、咬合力是控制飛砟重要有效途徑之一。

3)高速鐵路有砟道床中，飛砟發生概率受風荷載、負壓力系數影響，因此有必要進行高速鐵路有砟道床空氣動力學研究，通過有砟道床斷面及砟肩空氣動力學選型來抑制飛砟發生風險。

[1]井國慶.鐵路有砟道道床[M].北京:中國鐵道出版社, 2012.

JINGGuoqing.Railwayballast[M].ChinaRailwayPublishinghouse, 2012.

[2] 井國慶，王子杰，林建.基于力學平衡原理飛砟機理與防治研究[J].鐵道科學與工程學報, 2014, 11(6):28-33.

JINGGuoqing,WANGZijie,LINJian.Mechanicalequilibriumanalysisofballastflightmechanismandcounteractingmeasurement[J].JournalofRailwayandEngineering, 2014, 11(6):28-33.

[3] 宋佳寧，井國慶，黃紅梅.高速鐵路飛砟與防治[J].中國鐵路, 2015, 1(9):62-64.

SONGJiaoning,JINGGuoqing,HUANGHongmei.Ballastflyingofhighspeedrailwayanditsprevention[J].ChinaRailway, 2015, 1(9):62-64.

[4]QuinnD,HaywardM,BakerCJ,etal.Afullscaleexperime-ntalandmodellingstudyofballastflightunderhigh-speedtrains[J].RailRapidTransit, 2010, 12(6):86-93.

[5]JingGQ.ZhouYD,LinJ,etal.Ballastflyingmechanismandsensitivityfactorsanalysis[J] .SmartSens, 2012, 5(4):928-936.

[6]PremoliD,RocchiP,Schito.Ballastflightunderhigh-speedtrains:Windtunnelfull-scaleexper-imenttaltests[J].WindEng.Ind.Aerodynamic, 2015, 14(5):351-361.

[7]KaltenbachHJ,GautierPE,AgirreGM,etal.Assessmentoftheaerodynamicloadsonthetrackbedcausingballastprojection[C].Proceedingsofthe8thWorldConferenceonRailwayResearch, 2008.

[8]KwonHB,ParkCS.Anexperimentalstudyontherelationshipbetweenballast-flyingphenomenonandstrongwindunderhigh-speedtrain[C].ProceedingoftheWorldCongressonRailResearch, 2008.

[9]SimaM,VenkatasalamN.Investigationofcrosswindgroundconfigurationsforrailvehicles[C].InternationalWorkshoponTrainAerodynamics.Birmingham, 2013.

[10]SaussineG,MassonE,Thomas-Jean.Railwayballastflyingphenomenon:fromnumericalcomputationstowardriskassessment[C].EUROMECH509:VehicleAerodynamics,Berlin, 2009.

[11]KwonH,ParkC.Anexperimentalstudyontherelationshipbetweenballastflyingphenol-menonandstrongwindunderhighspeedtrain.WCRR[C]. 2006.

[12]SaussineG,AllainE,ParadotN,etal.Ballastflyingriskassessmentmethodforhighspeedline[C]//Proceedingsofthe9thWorldConferenceonRailwayResearch., 2011.

[13]ChenX,HuangG.Estimationofprobabilisticextremewindloadeffects:combinationofaerodynamicandwindclimatedata[J].EngMech, 2010, 13(6):747-760.

[14]FrancescoBJ,ErolT,MohdRS.Identificationofhigh-speedrailballastflightriskfactorsandriskmitigationstrategies[C]// 10thWorldCongressonRailwayResearchSydney,Australia, 2013.

[15]BakerCJ,DalleySJ,JohnsonT,etal.Theslipstreamandwakeofahigh-speedtrain[J].RailanRapidTransit,2001,215(2):83-99.

Reliability assessment on high speed railway ballast flight based on monte carlo

JINGGouqing,DINGDong,SHAOShuai

(Civil Engineering School, Beijing Jiaotong University, Beijing 100044, China)

Ballastflightisakeyprobleminfluencingtheapplicationanddevelopmentofballastedhighspeedtrack,whichisofrandom,discreteandcomplexnature.Inthepaper,basedonballastflightlimitstatefunction,theMonteCarlosimulationmethodwasusedtoquantifytheuncertainfactors,includingthedynamicballastbedandaerodynamiceffects.Thequantitativeprobabilityofoccurrenceandriskassessmentforballastflightwereinvestigated.Theresultsshowthattheoccurrenceprobabilityincreaseswithmeanwindvelocity,windpressurecoefficientsandtheaccelerationinducedbytrackbedvibration,anddecreaseswiththeballastmassandparticleinterlockforce.Theballastflightreliabilityissensitivelyinfluencedbyaerodynamiceffects,andtheHSRballastbedneedaerodynamicoptimization,suchasballastbedcrosssectionandshoulderballastdesignoptimizationtoreducetheriskofballastflight.

highspeedrailway;ballastflight;aerodynamic;dynamic;reliability

2015-11-07

國家自然科學基金資助項目(51578051)

井國慶(1979-)，男，河北廊坊人，副教授，博士，從事軌道工程研究；E-mail:gqjing@bjtu.edu.cn

U213.722

A

1672-7029(2016)07-1234-07