n！的質(zhì)因數(shù)分解的新發(fā)現(xiàn)

趙云平（滇西科技師范學院數(shù)理系，云南 臨滄 677099）

n！的質(zhì)因數(shù)分解的新發(fā)現(xiàn)

趙云平
（滇西科技師范學院數(shù)理系，云南 臨滄 677099）

n！的質(zhì)因數(shù)分解是高斯函數(shù)（或取整函數(shù)）在初等數(shù)論中的一個應用，針對n！的質(zhì)因數(shù)分解作了初步探討，通過實例給出n！的質(zhì)因數(shù)分解中質(zhì)因數(shù)指數(shù)的一種簡潔求法。

n！；質(zhì)因數(shù)；指數(shù)；分解

0　引言

把一個大于1的整數(shù)N分解成質(zhì)因數(shù)的乘積，要找出它所有的質(zhì)因數(shù)，首先找出的質(zhì)數(shù)，再判斷這些質(zhì)數(shù)是不是N的質(zhì)因數(shù)，最后把它寫成質(zhì)因數(shù)乘積的形式，這個工作量是非常大的。但是對于一類特殊的問題來說，把它分解成質(zhì)因數(shù)的乘積會比較容易一些，是什么樣的數(shù)呢？就是這個階乘。我們要討論階乘的分解，就要用到函數(shù)［X］，下面我們先來認識一些相關概念及結論。

1　預備知識［1-5］

定義1：在大于1的整數(shù)中，若某數(shù)p除了1和它本身以外沒有其它的因數(shù)，這種整數(shù)叫做質(zhì)數(shù)，也稱為素數(shù)。否則稱為合數(shù)。

定義2：把一個合數(shù)分解成若干個質(zhì)數(shù)乘積的形式，其中每個質(zhì)數(shù)都是這個合數(shù)的因數(shù)，叫做這個合數(shù)的分解質(zhì)因數(shù)。分解質(zhì)因數(shù)只針對合數(shù)。

定義3：若X∈R，函數(shù)［X］的值是不超過X的最大整數(shù)，我們把［X］叫做方括號函數(shù)或高斯函數(shù)，它是X的整數(shù)部分。

定理1：如果a是大于1的整數(shù)，則a的除1以外最小的正因數(shù)p一定是質(zhì)數(shù)，并且當a為合數(shù)，。

證明：因為a是大于1的整數(shù)，所以大于1的正因數(shù)一定存在，a本身就是一個。下面證明第1個結論：a的除1以外最小的正因數(shù)p一定是質(zhì)數(shù)，我們用反證法。

若p不是質(zhì)數(shù)，p就是合數(shù)，則p=p1p2，2≤p1，p2≤p，1＜p1＜p，且p1p，又因為p是a的因數(shù)，有p a，所以p1a，又p是大于1的，與p是a的大于1的最小正因數(shù)矛盾，所以p一定是質(zhì)數(shù)。

因為a是合數(shù)，設a=a1p，且a1＜1，p≤a1，p2≤ a1p=a，。

定理2（算術基本定理）：任一大于1的整數(shù)a能表示成質(zhì)數(shù)的乘積，即a＜1，則a=p1，p2，…，pn，p1≤p2≤…≤pn，其中p1是質(zhì)數(shù)，p1為a的質(zhì)因數(shù)。

［注意］

推論1：任一大于1的整數(shù)a能夠唯一地寫成a=p1a1，p2a2，…，pkak（稱為a的標準分解式），ai＞0，i= 1，2，…，k。其中pi＜pj（i＜j）。

［注意］

n！=1×2×…×n，故小于等于n的質(zhì)因數(shù)在n！中一定出現(xiàn)。

2　n！的質(zhì)因數(shù)分解的步驟

第一，先找≤n的所有質(zhì)數(shù)，即先寫出1到n的所有正整數(shù)，找到的質(zhì)數(shù)，在1到n的數(shù)中首先劃掉1，再劃掉的這些質(zhì)數(shù)的倍數(shù)，剩下的就是n以內(nèi)的質(zhì)數(shù)；

第二，應用定理3計算各質(zhì)因數(shù)的指數(shù)；

第三，若質(zhì)因數(shù)pi對應的指數(shù)為ai，則

n！=p1a1，p2a2，…，prar

例如算20！的質(zhì)因數(shù)分解。

方法一：

分析：因為20！=1×2×3×4×5×6×7×8×9×10×11× 12×13×14×15×16×17×18×19×20，故不超過20的質(zhì)數(shù)在20！的質(zhì)因數(shù)分解式中一定出現(xiàn)。1既不是質(zhì)數(shù)也不是合數(shù)，去掉1，質(zhì)數(shù)2、3、5、7、11、13、17、19保留，接下來把剩余合數(shù)4、6、8、9、10、12、14、15、16、18、20用質(zhì)因數(shù)分解的常規(guī)方法——短除法進行分解，就是先用一個合數(shù)的最小質(zhì)因數(shù)去除這個合數(shù)，得出的數(shù)若是一個質(zhì)數(shù)，就把這個合數(shù)寫成質(zhì)因數(shù)相乘的形式；剩余若仍然是一個合數(shù)，就繼續(xù)按原來的方法分解，直至最后是一個質(zhì)數(shù)，短除法就結束。如，合數(shù)4，它的最小質(zhì)數(shù)是2，4=2×2；合數(shù)6，它的最小質(zhì)數(shù)是2，6=2×3；合數(shù)8，它的最小質(zhì)數(shù)是2，8=2×4，4再可以分解，8=2×2×2；合數(shù)9，它的最小質(zhì)數(shù)是3，9=3×3；類似的10=2×5，12=2×2×3，14=2×7，15=3×5，16=2×2×2×2，18=2×3×3，20=2×2× 5。

綜上，20！=2×3×2×2×5×2×3×7×2×2×2×3×3×2× 5×11×2×2×3×13×2×7×3×5×2×2×2×2×17×2×3×3× 19×2×2×5

即

20！=218×38×54×72×11×13×17×19

從計算上看，方法一比較繁瑣，當合數(shù)增大時計算量隨之增大，故此方法只適用于不太大的合數(shù)，特別是對于n！這類特殊的數(shù)，不建議使用此方法。

方法二：

分析：將不超過20的正整數(shù)排列如下

12345678910

11 12 13 14 15 16 17 18 19 20

先找≤20的質(zhì)數(shù)，即先找≤＜5的質(zhì)數(shù)，有2和3，首先把1劃去，然后從1至20的數(shù)中劃去2和3的倍數(shù)，剩下的就是20以內(nèi)的質(zhì)數(shù)：

故≤20的質(zhì)數(shù)有2、3、5、7、11、13、17、19，下面分別計算2、3、5、7、11、13、17、19的指數(shù)。

2的指數(shù)

3的指數(shù)

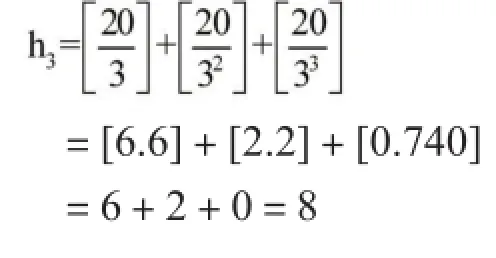
5的指數(shù)

7的指數(shù)

11的指數(shù)

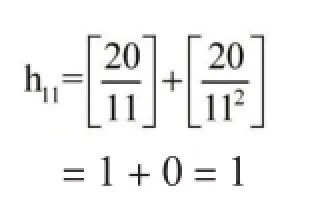
13的指數(shù)

17的指數(shù)

19的指數(shù)

所以20！=218×38×54×72×11×13×17×19

從指數(shù)計算的過程中發(fā)現(xiàn)∶，依此類推，可以推廣到有限個的情形。

則上述例題中指數(shù)的求法如下：

5的指數(shù)

這種新方法的優(yōu)點在于不需要計算pr，只需在上一結果的基礎上進行計算，特別對于p和r太大時，此方法可大大減少計算量；缺點在于，由于下一步的操作是在前一步的基礎上進行，一旦前一步發(fā)生錯誤，就會出現(xiàn)連帶作用，以致后面的結果也是錯誤的，所以希望大家用此方法時確保每一步準確無誤，避免計算的損失。

總之，方法二較方法一而言，方法更簡捷直接，不需要重復計算，對質(zhì)因數(shù)指數(shù)的計算一步到位，方法二更適用于n！的質(zhì)因數(shù)分解。

3　結語

質(zhì)因數(shù)分解包含了對質(zhì)因數(shù)的認識及對因數(shù)分解的掌握兩個基本內(nèi)容，文章雖然重點討論n！的質(zhì)因數(shù)分解，但是對于任何大于1的整數(shù)N的質(zhì)因數(shù)分解也是類似的，不同的是，不用找出≤N的所有質(zhì)數(shù)，只需篩選出的質(zhì)數(shù)之后，判斷這些質(zhì)數(shù)是不是N的因數(shù)，更多相關的問題有待進一步探討。

［1］潘承洞，潘承彪.初等數(shù)論［M］.北京大學出版社，2002:48-60.

［2］閔嗣鶴，嚴士健.初等數(shù)論［M］.3版.北京:高等教育出版社，2003:14-23.

［3］課程教材研究所.初等數(shù)論［M］.北京:人民教育出版社，2006:50-61.

［4］胡典順，徐漢文.初等數(shù)論［M］.北京：科學出版社，2010:2-25.

［5］邊紅平.初等數(shù)論［M］.杭州：浙江大學出版社，2007:10-13.

ANew Discovery of Prime Factorizations of n！

ZHAO Yun-ping
（DepartmentofMathematics，DianxiScienceandTechnologyNormalUniversity，Lincang，Yunnan677099，China）

The prime factorizations of n！is an application of Gaussian function（or rounding function）［x］in elementary number theory.In view of the n！，the paper examines a preliminary discussion of the prime factors decomposition and put forward a simplified solution of prime factors index in the decomposition of prime factor of n！through specific examples.

n！；Prime Factors；Index；Decomposition

O156.2

A

1673-1891（2016）02-0021-03

10.16104/j.issn.1673-1891.2016.02.006

2016-03-24

趙云平（1982—），女，云南臨滄人，碩士，講師，研究方向:基礎數(shù)學數(shù)論應用，運籌學線性規(guī)劃，數(shù)值代數(shù)。