多約束條件下反演滑模制導律設計*
劉 琳,曹小軍,陳 韻,苗昊春,馬 菲(中國兵器工業第203研究所,西安 710065)
多約束條件下反演滑模制導律設計*
劉琳,曹小軍,陳韻,苗昊春,馬菲
(中國兵器工業第203研究所,西安710065)
為了實現最佳毀傷效應,導彈一般同時要求具有較高的制導精度和與戰斗部相匹配的落角。基于導彈末端視線角速度和落角多約束條件,文中結合滑模變結構控制和反演法設計了一種反演滑模制導律。建立了導彈與目標相對運動方程和末端視線角速度及落角多約束下的線性化模型,采用反演滑模設計方法設計了制導律,最后進行了六自由度數字仿真,結果表明該制導律能有效實現期望落角和中靶精度,滿足設計要求。關鍵詞:反演滑模;制導律;視線角速度;落角
0 引言
制導律是導彈在接近目標的整個過程中應遵循的運動規律,它根據導彈與目標的相對位置、相對運動關系將導彈導向目標,對導彈的速度、機動過載、命中精度、毀傷效應等均有直接影響,是導彈制導系統設計的關鍵。滑模變結構控制本質上是一類特殊的非線性控制,這種控制策略的“結構”可以在動態過程中根據系統當前的狀態有目的的不斷變化,迫使系統按照預定的“滑動模態”軌跡運動。反演設計方法的基本思想是將非線性系統分級成若干個不超過系統階數的子系統,然后為每個子系統分別設計李亞普諾夫函數和中間虛擬控制量,一直“后退”到整個系統,直到完成整個控制律的設計,使整個系統滿足期望的動靜態性能指標。
文中提出的多約束條件下反演滑模制導律設計是將反演設計方法與滑模變結構控制方法結合,采用導彈末端視線角速度和落角多約束下的線性化模型,推導出穩定的制導律,保證導彈準確命中目標的同時滿足期望落角的設計要求。針對攻堅戰斗部等需要小落角的戰斗部,可以根據減小期望落角達到設計要求,對于穿甲戰斗部、侵徹戰斗部等大多數需要大落角的戰斗部,同樣可以滿足大期望落角的設計要求,相對于傳統制導律,在相同情況下,大幅增大了落角,提高了制導精度,增大戰斗部的毀傷效應。
1 相對運動方程
根據運動學方法分析可得相對運動方程組:
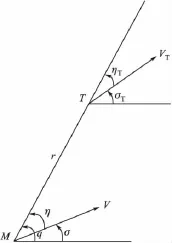
圖1 導彈與目標的相對位置
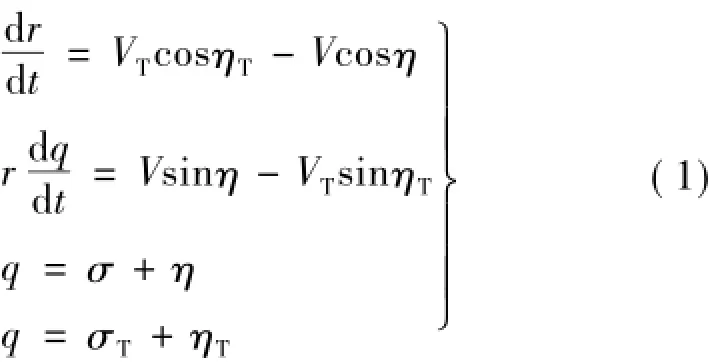
式中:r為彈目距離;q為彈目線方位角;V、VT分別為導彈、目標的速度;σ、σT分別為導彈、目標速度方向與基準線的夾角;η、ηT分別為導彈、目標速度方向與彈目線之間的夾角。
2 線性化模型
通常情況下,導彈的運動一般可以分解為縱向運動和側向運動,文中研究導彈在縱向平面內的運動。
在縱向平面內,定義落角σ0為命中目標時刻導彈速度矢量與目標速度矢量之間的夾角:
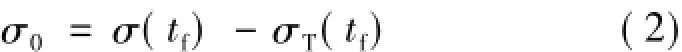
導彈的期望落角為σ*,在末端時刻若想以期望落角命中目標,則在末制導結束時刻設置如下約束條件:
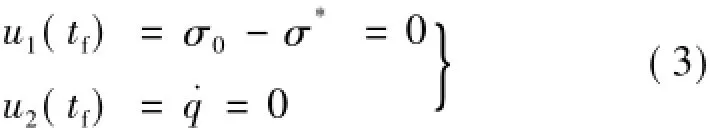
若u2(tf)為零,即導彈在結束時刻視線角速度˙q為零,則表示導彈能夠準確命中目標,若同時u1(tf)為零,則表示導彈能夠以期望落角σ*命中目標。因此,在視線角速度與落角多約束條件下的反演滑模制導律設計就是要滿足導彈以期望落角在末端時刻準確擊中目標。
在導彈飛行的末制導段可以近似認為q≈σ0,因此,可以將u1重新定義為:

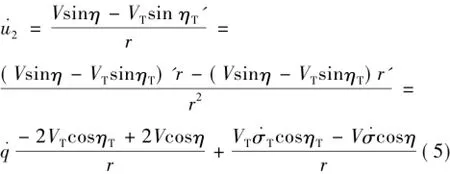
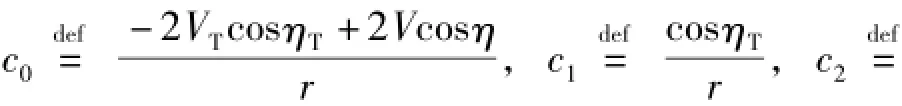
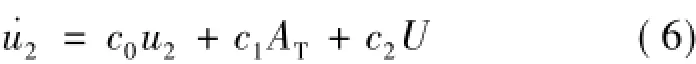
因此,多約束條件下的導彈線性化模型為:
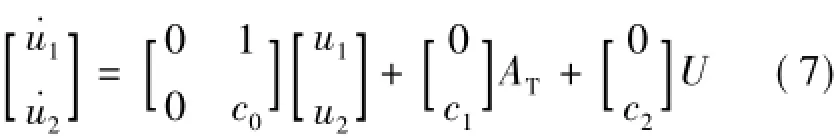
3 反演滑模制導律設計
3.1基本原理
對于靜止目標而言:
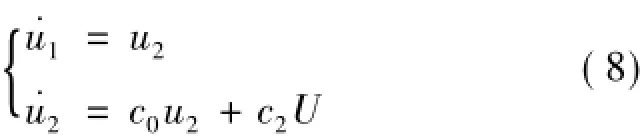
為了保證命中目標時刻u1為零,定義誤差z1=u1-0=u1,則
基本的反演方法設計步驟分以下兩步:
a)定義Lyapunov函數

則:
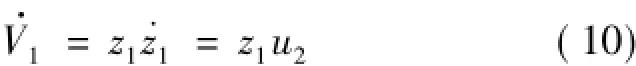
取u2=-m1z1+z2,其中m1>0,則:
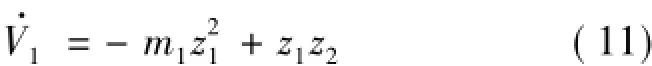
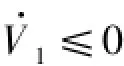
b)定義Lyapunov函數
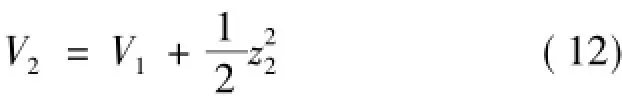
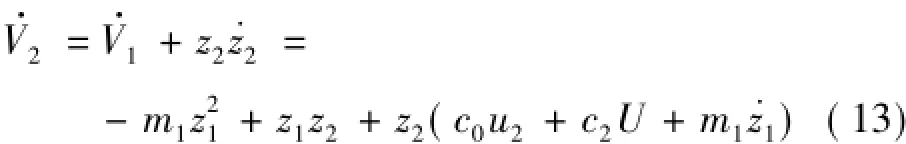
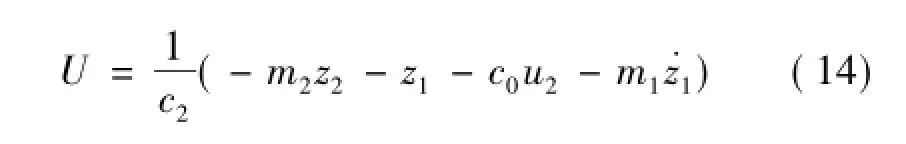
其中,定義m2≥0,則:
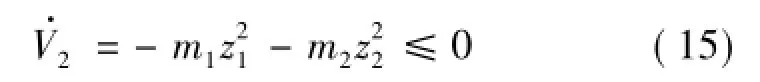
由于z2=u2+m1z1,則當 z1→0和 z2→0時,u2→0。
通過制導律U的設計,使得系統滿足了李雅普諾夫穩定性理論條件,z1和z2漸近穩定,從而保證系統具有全局意義下的漸近穩定性,并且z1以指數形式漸近收斂于零。
3.2制導律設計
僅采用反演設計方法設計制導律需要導彈線性化模型的精確信息,將反演設計方法與滑模變結構控制相結合,擴大反演設計方法的試用范圍,增強系統的魯棒性。
考慮系統擾動為d,|d|≤D,導彈的線性化模型變為:
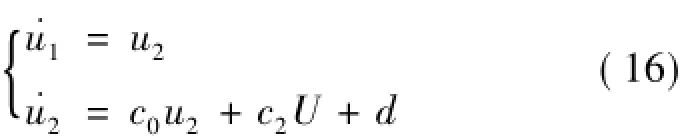
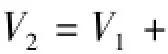
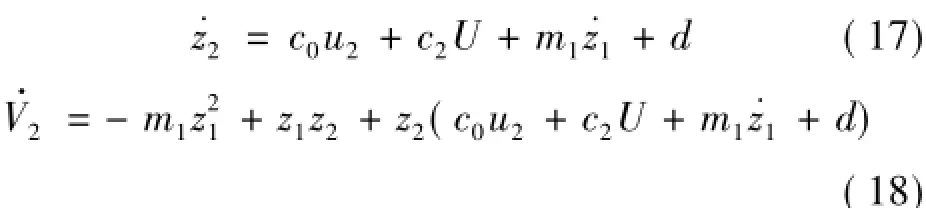
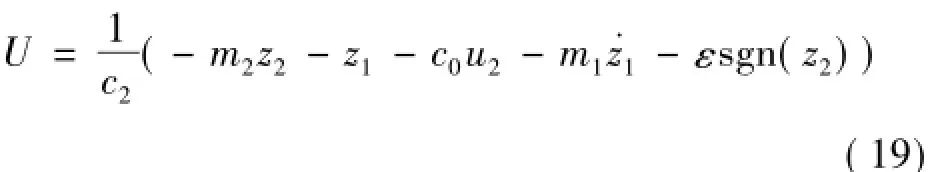
式中:m2為大于零的正常數,ε≥D,則:
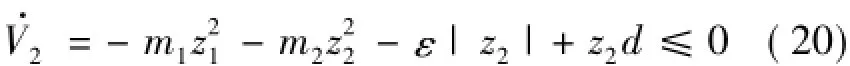
對于運動目標而言,制導律的設計同靜止目標,制導指令依舊選擇:
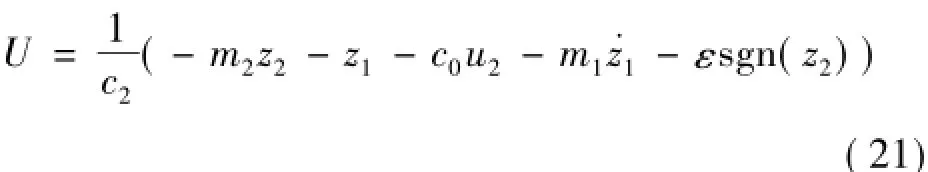
式中:|c1AT|≤D,ε≥D,則:
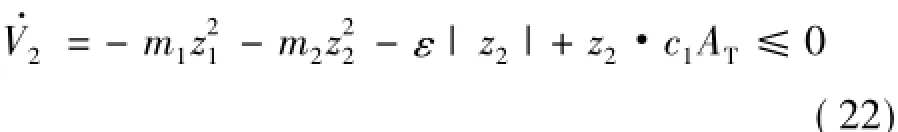
4 仿真結果及分析
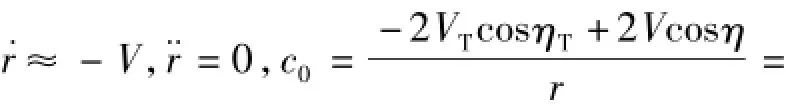
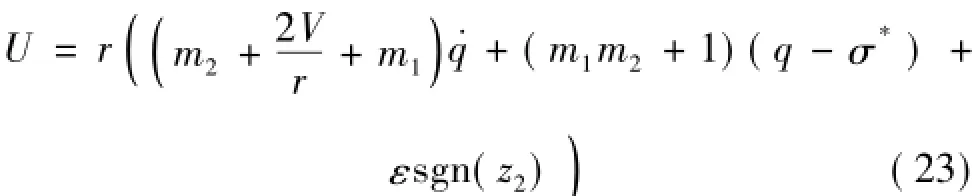
其中,制導律U的第一項能夠保證導彈準確命中目標,第二項保證命中點處導彈速度方向、落角等滿足要求,第三項保證制導律的精度,增強系統的魯棒性。
假設目標為靜止目標,初始彈目距離為8 000 m,導彈末制導段采用反演滑模制導律,彈目距離為4 000 m時進入末制導,對導彈進行六自由度數字仿真。圖2為期望落角為-30°時采用反演滑模制導律與比例導引律的導彈落角對比曲線,采用反演滑模制導律的導彈落角達到-30°,滿足落角約束條件,同時遠大于導彈采用傳統制導律時的落角。圖3為圖2條件下的導彈視線角速度對比曲線,采用反演滑模制導律的導彈視線角速度在飛行末端趨于零,滿足視線角速度約束條件,雖然視線角速度在制導過程中大于傳統比例導引律的視線角速度值,但仍保持在較小的范圍之內。圖4、圖5為期望落角分別為 -10°,-30°,-50°時采用反演滑模制導律的導彈落角和視線角速度曲線,三種條件下均滿足落角和視線角速度約束,可以滿足大落角和小落角的不同需求,雖然隨著落角的增大,制導過程中的視線角速度成增大趨勢,但仍保持在導引頭的跟蹤范圍之內。
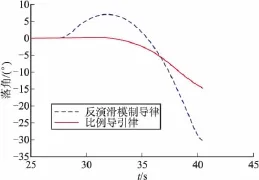
圖2 落角對比曲線

圖3 視線角速度對比曲線
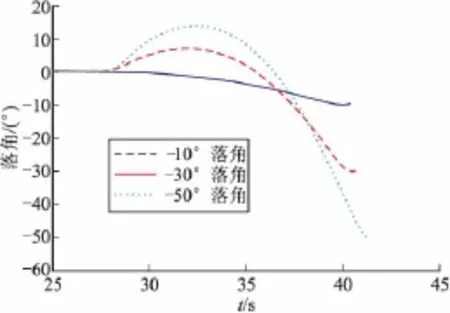
圖4 落角曲線
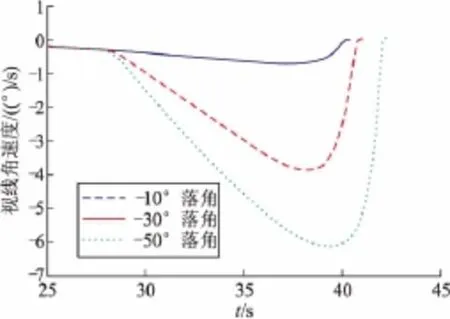
圖5 視線角速度曲線
5 結論
文中在約束導彈飛行末端視線角速度及落角的條件下設計了一種反演滑模制導律,在末端兩種約束條件均達到設計要求。導彈飛行末端視線角速度為零,提高了導彈的命中精度;針對不同戰斗部的需求滿足不同期望落角的設計要求,相同期望落角條件下,相對于傳統制導律,大幅度增大了落角,提高了制導精度,增大了戰斗部的毀傷效應;同時這種反演滑模制導律設計簡便,易于工程實現。在文中基礎上,考慮各種擾動因素帶來的影響,增加反演滑模制導律的魯棒性和自適應性,在實現大落角攻擊時適當減小視線角速度等問題值得進行進一步研究。
[1] 劉金琨.先進PID控制MATLAB仿真[M].北京:電子工業出版社,2013:256-278.
[2]錢杏芳,林瑞雄,趙亞男.導彈飛行動力學[M].北京:北京理工大學出版社,2012:91-112.
[3] 劉興堂.精確制導、控制與仿真技術[M].北京:國防工業出版社,2006:151-181.
[4]吳鵬.帶末端攻擊角度約束的制導方法研究[D].哈爾濱:哈爾濱工業大學,2009.
[5]孫未蒙,鄭志強.多約束條件下對地攻擊的最優制導律[J].兵工學報,2008,29(5):567-571.
[6]董晨,晁濤,王松艷.多約束下考慮控制飽和的自適應末制導方法[J].宇航學報,2014,35(6):677-684.
[7]盧鶯,張安,何海峰.圖像制導導彈落角約束的制導律設計[J].彈箭與制導學報,2011,31(5):57-60.
[8]MOON J,KIM K,KIM Y.Design of missile guidance law via variable structure control[J].Journal of Guidance,Control,and Dynamics,2001,24(4):659-664.
Design of Backstepping-sliding-mode Guidance Law under Multiple Constraints
LIU Lin,CAO Xiaojun,CHEN Yun,MIAO Haochun,MA Fei
(No.203 Research Institute of China Ordnance Industries,Xi’an 710065,China)
In order to achieve best damage,high precision of guidance and impact angle matching with warhead are required.In this paper,a backstepping-sliding-mode guidance law was designed based on sliding-mode variable structure control and the method of backstepping under multiple constraints of terminal LOS-rate and impact angle.The equation of relative motion between missile and target and the linearized model based on the constraints of terminal LOS-rate and impact angle were established,the guidance law was designed by backstepping-sliding-mode.Finally,6DOF simulation of missile shows that the guidance law can realize the expected impact angle and hitting precision effectively,meeting the requirements of design.
backstepping-sliding-mode;guidance law;LOS-rate;impact angle
TJ765.3
A
10.15892/j.cnki.djzdxb.2016.01.012
2015-09-14
劉琳(1991-),女,遼寧海城人,碩士研究生,研究方向:制導與控制。

