對(duì)水火箭發(fā)射速度和射程的理論研究
廖立楊 楊曉冬
(1廣東梅縣東山中學(xué),廣東 梅州 514015;2嘉應(yīng)學(xué)院物理與光信息科技學(xué)院,廣東 梅州 514015)
?
對(duì)水火箭發(fā)射速度和射程的理論研究
廖立楊1楊曉冬2
(1廣東梅縣東山中學(xué),廣東 梅州514015;2嘉應(yīng)學(xué)院物理與光信息科技學(xué)院,廣東 梅州514015)
本文利用功能原理及理想氣體絕熱方程,推導(dǎo)獲得水火箭發(fā)射初始速度、噴水時(shí)間以及射程的表達(dá)式.利用上述表達(dá)式對(duì)水火箭發(fā)射的初始速度、噴水時(shí)間及射程進(jìn)行了理論計(jì)算,并對(duì)水火箭內(nèi)盛裝水的體積和發(fā)射角度的最佳值進(jìn)行了理論計(jì)算與研究.
水火箭;功能原理;理想氣體絕熱方程;初始速度
水火箭是備受廣大中學(xué)生喜愛的科技制作.近年來,水火箭比賽在許多中學(xué)廣受歡迎,開展得如火如荼[1-5].目前有關(guān)水火箭的文獻(xiàn)報(bào)道主要采用實(shí)驗(yàn)方法,對(duì)水火箭射程及結(jié)構(gòu)改進(jìn)進(jìn)行了研究,而對(duì)于水火箭發(fā)射過程缺乏較為詳細(xì)的定量理論分析,缺乏對(duì)水火箭發(fā)射初速度及射程進(jìn)行理論計(jì)算的方法及相關(guān)理論.本文對(duì)水火箭的發(fā)射初速度、射程及噴水時(shí)間的進(jìn)行較為詳細(xì)的理論分析與研究,以獲得水火箭的發(fā)射初速度、射程及噴水時(shí)間理論表達(dá)式.
1 水火箭發(fā)射理論分析

圖1 水火箭結(jié)構(gòu)示意圖
水火箭結(jié)構(gòu)如圖1所示,在可樂瓶?jī)?nèi)灌入一定量的水并封閉一定質(zhì)量的空氣.發(fā)射時(shí),利用打氣筒不斷充入空氣,當(dāng)壓力超過橡皮塞能與瓶口間的最大摩擦力時(shí),瓶口與橡皮塞脫離,壓縮空氣把水從火箭尾部的瓶口向后高速噴出,水火箭依靠噴射水的反沖力,在短時(shí)間內(nèi)獲得較高的發(fā)射速度,之后靠慣性在空中滑翔飛行.為減小水火箭在飛行過程中的空氣阻力,在水火箭前端通常固定尖狀導(dǎo)流罩,同時(shí)在水火箭前端固定沙袋配重來提高水火箭重心,以保證水火箭平穩(wěn)飛行.
2.1水火箭發(fā)射初速度理論研究
為研究水火箭發(fā)射初速度,我們利用功能原理建立水火箭發(fā)射過程的運(yùn)動(dòng)方程.為簡(jiǎn)便計(jì),我們還將忽略一些次要因素.首先,由于瓶體的截面積比瓶口面積大較多,瓶?jī)?nèi)水相對(duì)瓶體的速度遠(yuǎn)小于水的噴出速度,同時(shí)也遠(yuǎn)小于瓶體運(yùn)動(dòng)速度,所以忽略瓶?jī)?nèi)水的速度,認(rèn)為瓶?jī)?nèi)水與瓶體具有相同的運(yùn)動(dòng)速度;同時(shí)彈體較重、速度不太快,空氣阻力也忽略.

圖2 水火箭發(fā)射工程示意圖
圖2(a)為瓶?jī)?nèi)水噴射過程中,t時(shí)刻水火箭示意圖,設(shè)該時(shí)刻水火箭總體質(zhì)量為m,瓶體質(zhì)量為m0,水火箭的發(fā)射速度為u,瓶?jī)?nèi)液面高度為h,瓶?jī)?nèi)氣體壓強(qiáng)為p,瓶外大氣壓強(qiáng)為pm.在瓶?jī)?nèi)氣體及外界大氣壓力作用下,設(shè)dt時(shí)間微元內(nèi),體積為dV,質(zhì)量為dm的水噴出瓶口,其相對(duì)地面的噴射速度為v,同時(shí)在反沖力的作用下,水火箭發(fā)射速率增加du,如圖2(b)所示.假設(shè)瓶?jī)?nèi)水為理想流體,根據(jù)功能原理,dt時(shí)間內(nèi),水火箭機(jī)械能增量可表示為
(1)
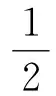
(2)
設(shè)噴水過程中,水相對(duì)于瓶體的噴射速度為vr,則式(2)可表示為
(3)
在上述噴水發(fā)射過程中,瓶?jī)?nèi)氣體對(duì)水的壓力為內(nèi)力,水火箭所受重力為外力.若水火箭使用體積為1.25L的可樂瓶,其瓶體直徑為9cm,設(shè)瓶?jī)?nèi)氣體壓強(qiáng)為3倍標(biāo)準(zhǔn)大氣壓(實(shí)驗(yàn)表明,水火箭瓶?jī)?nèi)可承受最大氣壓值可達(dá)10個(gè)標(biāo)準(zhǔn)氣壓),此時(shí)瓶?jī)?nèi)的壓力約為2400N,而水火箭所受重力約為10N,因此在水火箭噴射過程中,系統(tǒng)所受重力可忽略,整個(gè)噴水發(fā)射過程動(dòng)量守恒,則可得:
(4)
將式(4)展開可得:
(5)
將式(5)代入式(4)并展開可得:
(6)
式(6)中,水火箭噴射水的與瓶氣內(nèi)體體積變化量dV間滿足:
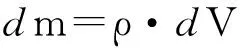
(7)
將式(5)、(7)代入式(6)可得:
(8)
利用分離變量法,根據(jù)式(8),可將水火箭在噴水過程中所獲得的發(fā)射速度表示為
(9)
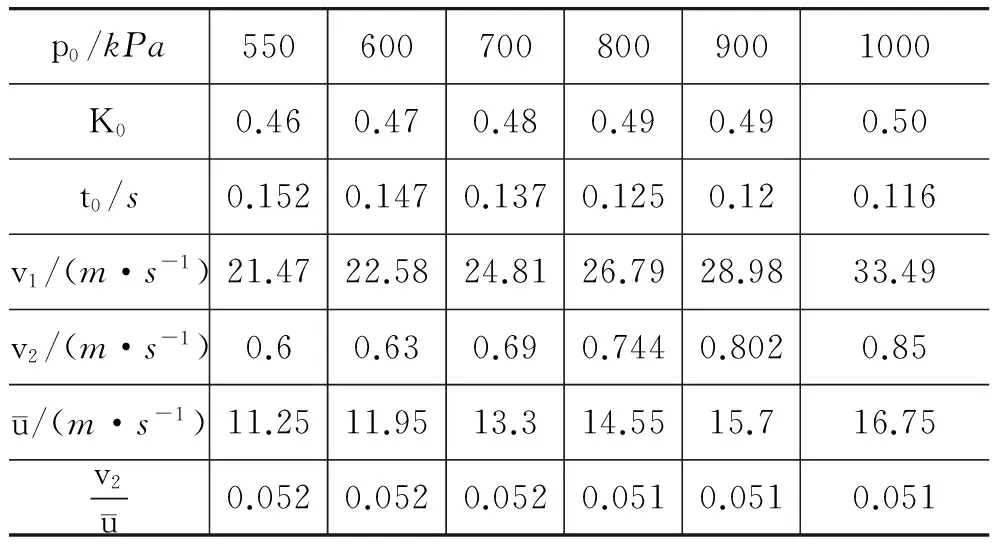
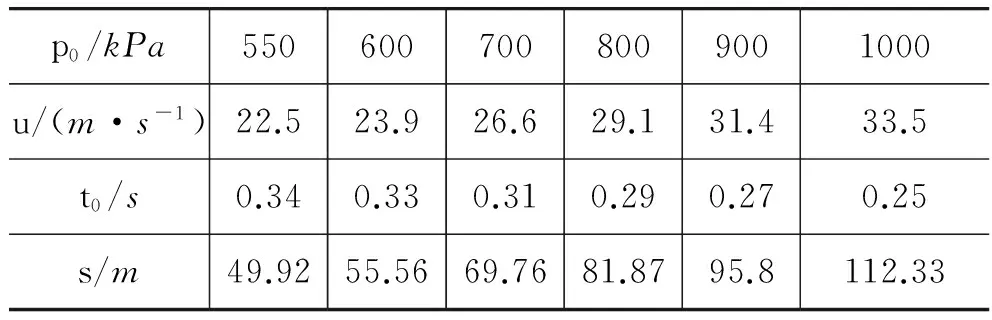
上式中,積分變量為發(fā)射過程中,噴出水的質(zhì)量.積分上限中,m0為瓶?jī)?nèi)水噴射完后瓶體的質(zhì)量,M為水火箭初始時(shí)刻質(zhì)量,其值應(yīng)為噴射水的總質(zhì)量與m0之和.由于發(fā)射時(shí)間較短,且瓶體隔熱性較好,瓶?jī)?nèi)氣體在膨脹過程中無法與外界完成熱交換,因此可認(rèn)為在噴水過程中,瓶?jī)?nèi)氣體做絕熱膨脹.下面我們將利用理想氣體狀態(tài)方程,對(duì)式(9)做變量變換,以便利用數(shù)值法對(duì)式(9)進(jìn)行求解.設(shè)瓶體的容積為V0,在噴水過程的初始時(shí)刻,瓶?jī)?nèi)氣體壓強(qiáng)為p0,瓶?jī)?nèi)水的體積為k0V0,0 (10) 式中,0≤k (11) 設(shè)噴水過程中,任意時(shí)刻壓強(qiáng)為p,由式(10)、式(11)及理想氣體絕熱方程可得: (12) 上式中,γ為空氣的比熱容比,其值為7/5.對(duì)式(12)變形可得: (13) 式(13)中,壓強(qiáng)p為k的函數(shù).在噴水過程中,任意時(shí)刻瓶?jī)?nèi)水的質(zhì)量可表示為 (14) 在噴水過程的初始時(shí)刻,瓶?jī)?nèi)水的質(zhì)量為 (15) 由式(14)及式(15)可得噴水過程中,任意時(shí)刻水火箭的質(zhì)量為 (16) 由于dt時(shí)間內(nèi)噴射水的質(zhì)量與dt時(shí)間內(nèi)水火箭質(zhì)量變化量相同,所以dt時(shí)間內(nèi)噴射水的質(zhì)量可表示為 (17) 將式(13)、(15)、(16)、(17)代入式(9)可得: (18) 由式(18)可以看出,水火箭發(fā)射初始速度u主要取決于水火箭初始時(shí)刻腔內(nèi)氣體壓強(qiáng)p0、初始時(shí)刻水火箭內(nèi)水體積與可樂瓶體積的比值k0以及水火箭噴水完畢后水火箭的質(zhì)量m0.其中瓶?jī)?nèi)初始?xì)怏w壓強(qiáng)p0主要由瓶塞與瓶體間摩擦力大小決定,實(shí)驗(yàn)表明,其值可達(dá)1000kPa;理論上說,水火箭噴水完畢后水火箭的質(zhì)量m0其值越小,噴水過程中所獲得的加速度就越大,最后獲得的發(fā)射速度也越大,但在實(shí)際發(fā)射過程中,為了保證火箭在空中不翻滾,須在其前端艙內(nèi)加沙作為配重,所以其值也不可能太小; k0是發(fā)射者能夠靈活控制的重要參數(shù).為了研究k0對(duì)于水火箭發(fā)射初速度的影響,設(shè)m0=0.3kg,V0=0.125L,外界氣壓pm=100kPa,利用式(18),我們分別計(jì)算初始?jí)簭?qiáng)p0為550kPa、700kPa、800kPa、1000kPa時(shí),水火箭發(fā)射初速度u隨k0變化曲線,計(jì)算結(jié)果如圖3所示.從圖3可以直觀看出,在壓強(qiáng)p0固定的條件下,當(dāng)k0為某一最佳值時(shí),水火箭發(fā)射初速度u最大.表1為根據(jù)式(18)計(jì)算所得,在不同初始?jí)簭?qiáng)p0下,水火箭發(fā)射速度u最大所對(duì)應(yīng)k0最佳值,同時(shí)也計(jì)算了u的最大值.從圖3及表1可直觀看出,隨著初始?jí)簭?qiáng)p0的增大,k0最佳值逐漸增大,且k0最佳值的變化范圍并不大,當(dāng)p0在550~1000kPa范圍內(nèi),k0最佳值在0.46~0.5之間. 圖3 水火箭發(fā)射初速度u隨k0變化曲線 p0/kPa5506007008009001000k00.460.470.480.490.490.50u/(m·s-1)22.523.926.629.131.433.5 2.2水火箭噴水時(shí)間理論研究 噴水過程所需要時(shí)間表達(dá)式可由下列步驟推導(dǎo):設(shè)瓶口的面積為S,則dt時(shí)間內(nèi),噴射水的體積為 (19) 根據(jù)式(11),dt時(shí)間內(nèi)瓶?jī)?nèi)氣體體積變化量dV可表示為: (20) 由(21)、(22)兩式可得: (21) 由(6)、(7)兩式可得: (22) 根據(jù)(13)、(21)、(22) 3式可得: (23) 由式(25)可得,噴水過程所需時(shí)間為 (24) 利用式(24),我們采用數(shù)值計(jì)算的方法,分別計(jì)算了水火箭初始?jí)簭?qiáng)為550kPa、600kPa、700kPa、800kPa、900kPa及1000kPa時(shí),發(fā)射過程的噴水時(shí)間,計(jì)算過程中,設(shè)瓶口瓶嘴的直徑1.5cm,對(duì)應(yīng)的面積為0.99cm2,瓶的容積為1.25L,瓶體直徑約為9cm,瓶體直徑為瓶口直徑的6倍,其橫截面面積為瓶口面積的36倍,所以瓶?jī)?nèi)水相對(duì)瓶體速度應(yīng)為瓶口噴水速度的1/36.k0為表1所給出的上述壓強(qiáng)下的最佳值,計(jì)算結(jié)果如表2所示.從計(jì)算結(jié)果可看出,隨著初始?jí)簭?qiáng)增大,噴水時(shí)間逐漸降低. 噴水過程中,瓶口水的平均噴射速度可以表示為 (25) 式中,d1為瓶口直徑,瓶?jī)?nèi)水的平均流動(dòng)速度可以表示為 (26) 表2 不同壓強(qiáng)對(duì)應(yīng)水火箭的噴水時(shí)間、相對(duì)瓶體噴水 表3 水火箭在不同初始?jí)簭?qiáng)下的射程 2.3水火箭射程計(jì)算 設(shè)水火箭以與地面為θ的發(fā)射角向遠(yuǎn)處發(fā)射,忽略空氣阻力,其運(yùn)動(dòng)可分為:噴水發(fā)射與斜拋運(yùn)動(dòng).其中第一階段噴水發(fā)射過程可分解為在噴射水反沖力作用下,沿與地面夾角為θ方向的變加速直線運(yùn)動(dòng)與自由落體運(yùn)動(dòng)的合成,當(dāng)噴水過程結(jié)束時(shí),水火箭沿水平方向與豎直方向的速度可表示為 (27) (28) 式中ux為噴射結(jié)束時(shí)水平,uy為噴射結(jié)束時(shí)豎直方向的速度,u為噴射結(jié)束時(shí)的速度,其值可由式(18)計(jì)算獲得.水火箭噴射過程上升高度可表示為: (29) (30) 噴射過程完成后,斜拋運(yùn)動(dòng)的運(yùn)動(dòng)方程為 (31) 式中t為水火箭完成整個(gè)斜拋運(yùn)動(dòng)所需時(shí)間,由式(31)可得 (32) 水火箭發(fā)射的總射程可表示為 (33) 將式(27)、(28)、(30)、(31)代入式(33)并展開得: (34) 上式中,不同壓強(qiáng)下的發(fā)射初速度u可由式(18)求得,噴水所用時(shí)間t0可由式(24)求得.利用式(34),我們計(jì)算瓶的體積V0=1.25L,噴口直徑為1.5cm,瓶體直徑為9cm,k0=0.5,m0=0.3kg,發(fā)射角度為45°時(shí),水火箭在不同初始?jí)簭?qiáng)下的射程.計(jì)算結(jié)果如表3所示. 由表3可見,隨著初始?jí)簭?qiáng)增大,射程逐漸增大;平均而言,壓強(qiáng)較大時(shí),射程隨壓強(qiáng)增大而增大的速率更快.利用式(34),我們又計(jì)算了初始?jí)簭?qiáng)p0=550kPa時(shí),水火箭在不同發(fā)射角度下的射程.計(jì)算結(jié)果如表4所示. 表4 水火箭在不同發(fā)射角度下的射程 從表4可以直觀看出,由于考慮了噴水過程水火箭的射程,水火箭發(fā)射的最佳角度約為47°,并非普通平拋運(yùn)動(dòng)對(duì)應(yīng)的45°. 通過對(duì)水火箭發(fā)射過程的理論研究,獲得水火箭發(fā)射初速度、噴水時(shí)間及射程計(jì)算公式,并利用上述公式對(duì)水火箭的發(fā)射初速度、噴水時(shí)間及射程進(jìn)行了理論計(jì)算.上述理論研究結(jié)論對(duì)于水火箭的設(shè)計(jì)及結(jié)構(gòu)優(yōu)化具有一定的指導(dǎo)意義. [1]方紅霞.關(guān)于水火箭水平射程的實(shí)驗(yàn)探究[J].物理實(shí)驗(yàn),2011(12):17-19. [2]楊慧迪,牛亮. 從實(shí)驗(yàn)與理論的雙重角度淺析影響水火箭飛行距離的因素[J].物理教師,2014(12):48-50. [3]汪海. 二級(jí)加壓水火箭的制作方法[J].物理實(shí)驗(yàn),2012(6):23-26. [4]梁法庫,梁帥.可以任意角度發(fā)射的水火箭[J].物理實(shí)驗(yàn),2010(10):31-32. [5]劉魯華,鄒東升,陳克俊.導(dǎo)彈工程專業(yè)“水火箭”案例設(shè)計(jì)與思考[J].高等教育研究學(xué)報(bào),2014(3):1672-1674. ■ THEORETICALINVESTIGATIONOFTHELAUNCHINITIALVELOCITYANDTHELAUNCHDISTANCEFORTHEWATERROCKET LiaoLiyang1YangXiaodong2 (1GradeThree,TungshunMiddleSchool,Meizhou,Guangdong514015;2SchoolofPhysicsandOpticalInformationTechnology,JiayingCollege,Meizhou,Guangdong514015) Accordingtotheprincipleofworkandenergyandidealgasadiabaticequation,theexpressionsoftheinitialvelocity,thetimeofjettingwater,andthelaunchdistanceofwaterrocketarededuced.Basedontheexpressions,theinitialvelocity,thetimeofjettingwater,andthelaunchdistanceofwaterrocketarecalculatedtheoretically.Optimumvolumeofwaterinthewaterrocketandthebestlaunchanglearealsoinvestigated. waterrocket;principleofworkandenergy;idealgasadiabaticequation;initialvelocity 2015-10-01; 2015-10-24 廖立楊,男,廣東梅縣東山中學(xué)高三年級(jí)學(xué)生,2014年獲第三十一屆全國(guó)中學(xué)生物理競(jìng)賽三等獎(jiǎng),2015年獲第三十二屆全國(guó)中學(xué)生物理競(jìng)賽一等獎(jiǎng). 引文格式: 廖立楊,楊曉冬. 對(duì)水火箭發(fā)射速度和射程的理論研究[J]. 物理與工程,2016,26(3):82-86.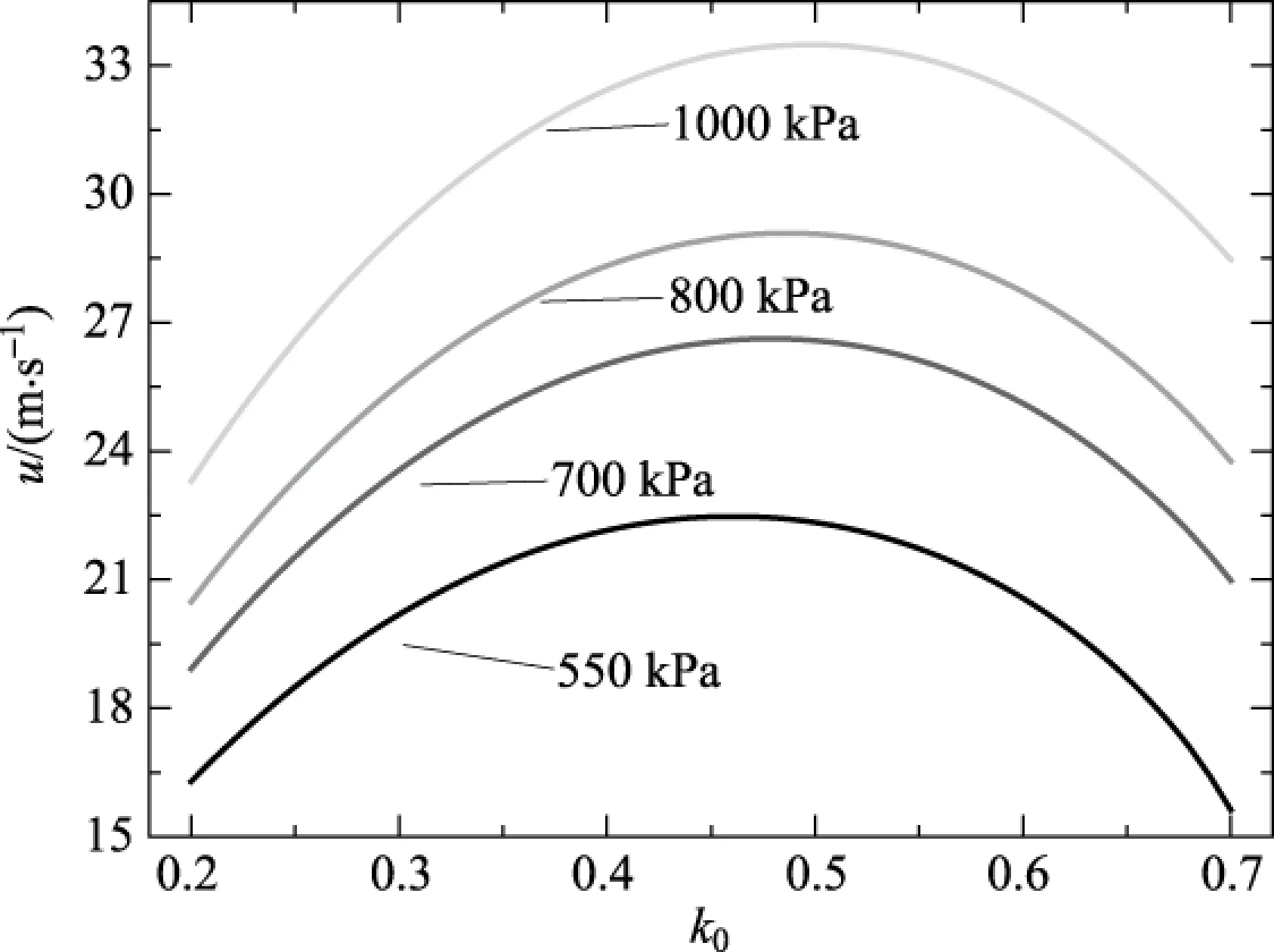

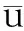




3 結(jié)語

