飛行器縱向非線性動力學建模對穩定性的影響

葉柳青, 葉正寅

(西北工業大學 翼型葉柵空氣動力學國家重點實驗室, 陜西 西安 710072)

?

飛行器縱向非線性動力學建模對穩定性的影響

葉柳青, 葉正寅

(西北工業大學 翼型葉柵空氣動力學國家重點實驗室, 陜西 西安 710072)

飛行器的穩定性分析與建立的動力學分析模型密切相關。傳統的穩定性分析方法是基于小擾動假設建立線性化模型，當飛行狀態中非線性特征明顯時,其結果誤差會帶來多大的影響是人們關心的問題。通過建立飛行動力學非線性模型和氣動力非線性模型,采用時間推進方法對兩類非線性問題進行了比較系統的研究。數值計算結果表明,飛行動力學非線性模型與線性模型相比,周期增大、幅值減小、衰減率增大;而非線性氣動力模型對周期幾乎沒有影響,但對幅值有一定的影響。

非線性方程; 非線性氣動力; 飛行動力學; 穩定性

0　引言

動力學模型中一類重要的非線性問題是氣動力非線性。氣動力非線性主要由氣體粘性產生,如激波與附面層相互作用、流動分離、不穩定渦流等均會引起氣動力非線性[1]。高超聲速飛行器通常是鈍頭前緣,并伴隨大迎角飛行,氣動力非線性現象嚴重,即使在小迎角下飛行,氣動力也是非線性的[2];另外,小展弦比機翼的翼尖渦會提供明顯的非線性升力,升力系數曲線斜率會增大,當展弦比較大時,斜率會隨著迎角減小[3];亞聲速聯翼布局的飛機在一定的迎角下,前翼繞流發生分離,影響后翼繞流流場,引起后翼氣動效率降低,導致全機俯仰力矩隨迎角發生非線性上仰[4]。因此,研究動力學模型中氣動力非線性對飛行器的穩定性影響很有必要。

除此之外,高超聲速飛行器的高度非線性、參數時變及通道間強耦合、飛行環境變化劇烈等特點使得自身穩定性較差[5]。根據傳統線化方法對高超聲速飛行器進行穩定性分析得到的動力學特性與真實值存在偏差。另一方面,飛行器在空中飛行時出現動不穩定,但是地面靜、動態風洞實驗測量(及數值模擬)結果是動穩定的[6]。因此,想要提高高超聲速飛行器的穩定性以及探索天地不一致的影響因素,建立非線性動力學模型來研究飛行器縱向穩定性,并研究動力學模型中的非線性對飛行器穩定性的影響是很有意義的。

在穩定性分析中,大多數文獻將六自由度直接簡化為單自由度或雙自由度進行研究,或是只有定性分析并沒有定量結果,或在應用非線性動力學模型對飛行器穩定性分析方面的研究并不全面。本文在此動機下,針對方程的此類線化處理對飛行器縱向穩定性的影響程度以及氣動力局部線化表示的影響程度試圖進行定量分析。首先推出了基于剛體假設的六自由度非線性動力學方程,依次分別對氣動力和方程進行線化,構造非線性氣動力模型,并將對應的非線性動力學模型進行數值仿真。將結果與小擾動線化穩定性分析結果進行對比,得到非線性動力學模型對飛行器穩定性的影響,對飛行器總體設計及穩定性分析具有一定的參考價值。

1　飛行器縱向運動模型

將飛行器視為質量固定不變的剛體,忽略地球曲率和自轉的影響。選定飛行器的狀態變量為:V,γ,q,α及θ,并且將方程的縱向和橫向解耦,運用牛頓運動定律導出飛行器縱向非線性動力學方程組為:

(1)

相關氣動力和力矩的計算參見文獻[7]。

2　飛行器縱向穩定性分析方法

上節導出的方程組是變系數、非線性的,一般無法求得解析解,只能數值求解。因此,傳統的穩定性分析方法一般是基于小擾動假設將方程進行線性化處理。

2.1方程的線化與氣動力的線性表征

方程的線化:將非線性動力學方程在基準點處泰勒展開,略去二階及二階以上的高階量。

氣動力線性表征為:

ΔT=TVΔV+THΔH+TδPΔδP

(2)

ΔD=DVΔV+DHΔH+DαΔα+DδeΔδe

(3)

ΔL=LVΔV+LHΔH+LαΔα+LδeΔδe+

(4)

MqΔq+MδeΔδe

(5)

式中:令操縱量Δδp=0,Δδe=0來討論飛行器縱向自由擾動運動的穩定性。不計擾動運動中高度變化引起的外力和力矩的影響。

2.2本文研究策略

(1)討論非線性氣動力對穩定性的影響

①在方程和氣動力都進行線化后的線性模型中,分別減小升力線斜率CLα,增大俯仰力矩線斜率Cmα,將得到的結果與之前得到的結果進行對比;

②方程線化,氣動力采用構造的非線性模型表示,將此非線性模型的求解結果與線性化模型的求解結果進行對比;

③方程非線性,即直接采用式(1),并且氣動力也采用構造的非線性模型,求解此非線性模型并將求解結果與線性模型的求解結果進行對比。

(2)討論非線性方程對穩定性的影響

將氣動力進行線化,方程非線性,求解此非線性模型并將求解結果與線性模型的求解結果進行對比。

3　仿真結果及分析

3.1非線性氣動力對穩定性的影響

3.1.1氣動導數CLα和Cmα對穩定性的影響

對于非線性氣動力條件下的飛行動態特性分析,目前仍然采用的是線化的處理方式,為了適應對于非線性氣動力問題分析的需要,只是用非線性狀態下的氣動導數來替代線性狀態下的氣動導數。因此,氣動導數的選取對于穩定性的分析很重要。本節的研究思路是基于線性模型,分析氣動導數的變化對飛行器縱向穩定性的影響。

由于想要找到數據較為全面的有關高超聲速飛行器的算例比較困難,因此本文以某低馬赫數的運輸機為算例。采用文獻[7]提供的某型通用航空飛機的飛行參數,對采用線性模型求得的解析解進行分析，并采用Matlab軟件進行數值仿真驗證。數值仿真的初始瞬時給定擾動Δα=1°,時間間隔為0.01 s。

解析解計算結果顯示:CLα從4.44減小到0.24,一直得到兩對共軛復根,說明周期性振蕩衰減運動的性態沒有改變;隨著CLα的減小,短周期和長周期的特征根實部絕對值呈線性減小,對應的半衰期增大,表明收斂速度隨著CLα減小而變慢。表1針對最大與最小的CLα得到的特征根和模態運動參數進行了對比。從表1中可看出,短周期和長周期的半衰期分別增大了61.31%和7.55%,可見CLα的變化對短周期的影響較大,但絕對改變量都在數秒量級,表明CLα的減小對收斂速度的影響很小。

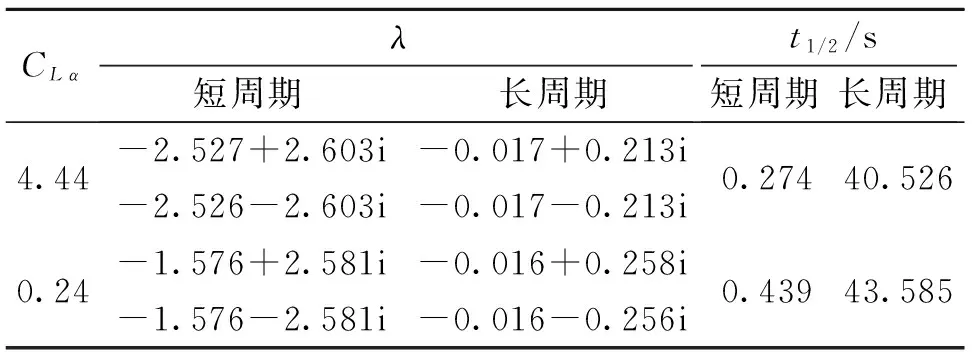
表1　響應模態結果對比Table1　Comparisonofresponsemodes

圖1為在不同CLα下速度的時間響應曲線。在本文所有的數值仿真中,Δα,Δq，Δθ和ΔV的定性變化規律相同,只是改變量有所差異,所以大多數只給出速度的時間響應曲線。從圖1中可見,隨著CLα的減小,收斂速度變化不大,并且振蕩周期會變小,振蕩幅值會增大，這與解析解結果一致。

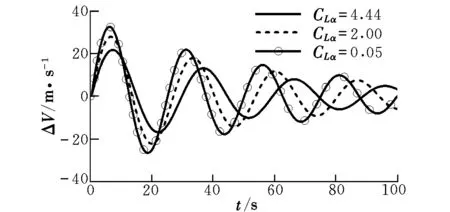
圖1　不同CLα條件下的速度對比Fig.1　Comparison of velocities on different CLα

圖2和圖3為特征根分布情況。從圖2和圖3中可見,Cmα從-0.683增大到0.140時,長周期和短周期的復數特征根都向實軸靠攏,短周期首先蛻化為實根。短周期和長周期在蛻變為實根前,實部變化很平緩,說明收斂速度幾乎不變。復根蛻化為實根后,分別向正、負實軸發展,隨著Cmα的增大,長周期也蛻化為實根并首先出現正實根,運動發散。

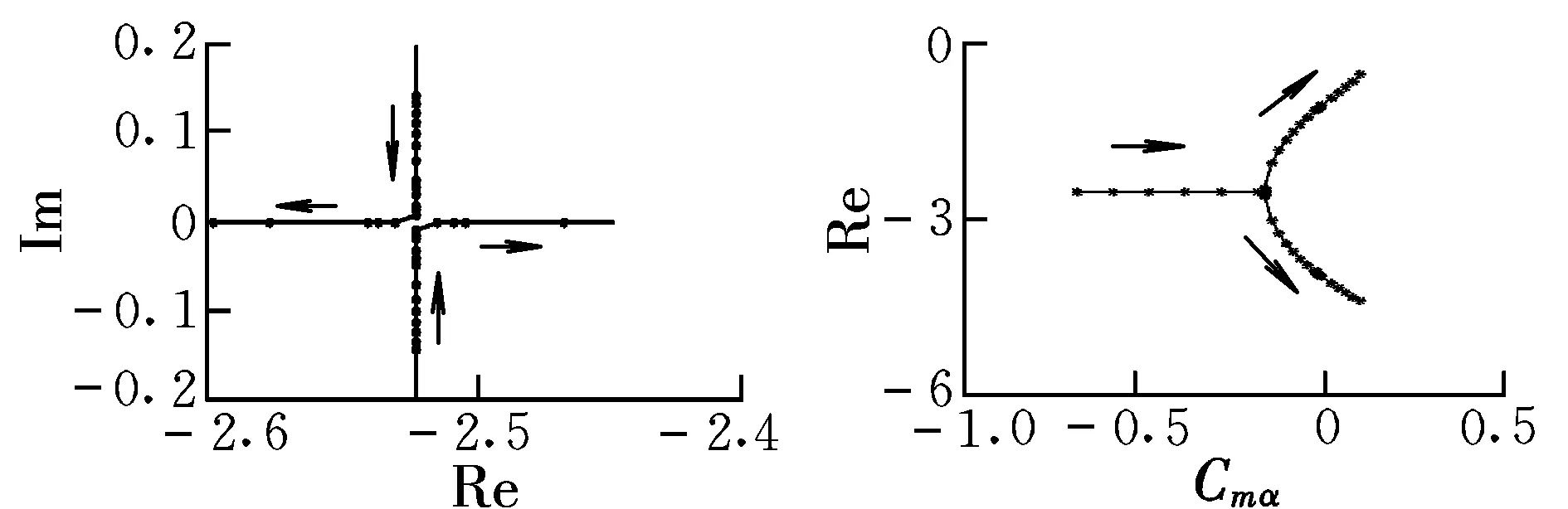
圖2　短周期特征根分布Fig.2　Characteristic root distribution of short-period

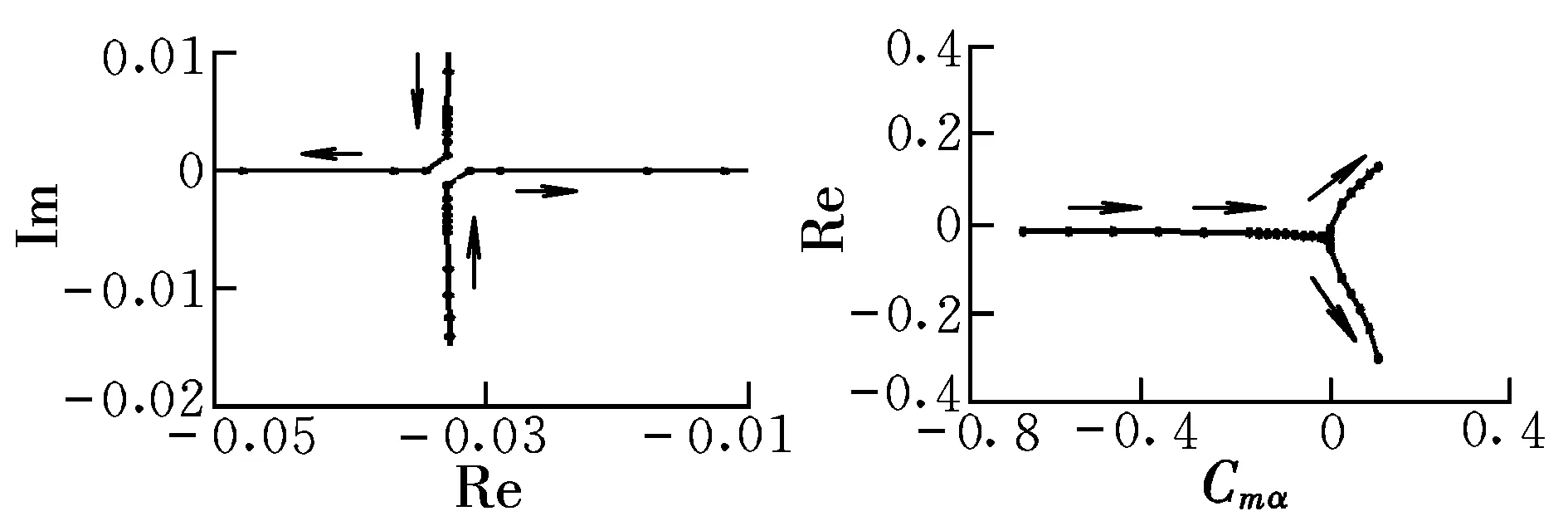
圖3　長周期特征根分布Fig.3　Characteristic root distribution of long-period

圖4為不同Cmα條件下的速度對比曲線。由圖4可見,Cmα在開始變化時,收斂速度基本不變,這與解析解分析一致。隨著Cmα的增大,振蕩周期增大,振蕩幅值減小,但各個飛行參數增大的量值又不盡相同。當Cmα增大56%時,ΔV,Δα,Δq和Δθ分別減小了30%,64%,45%和39%。

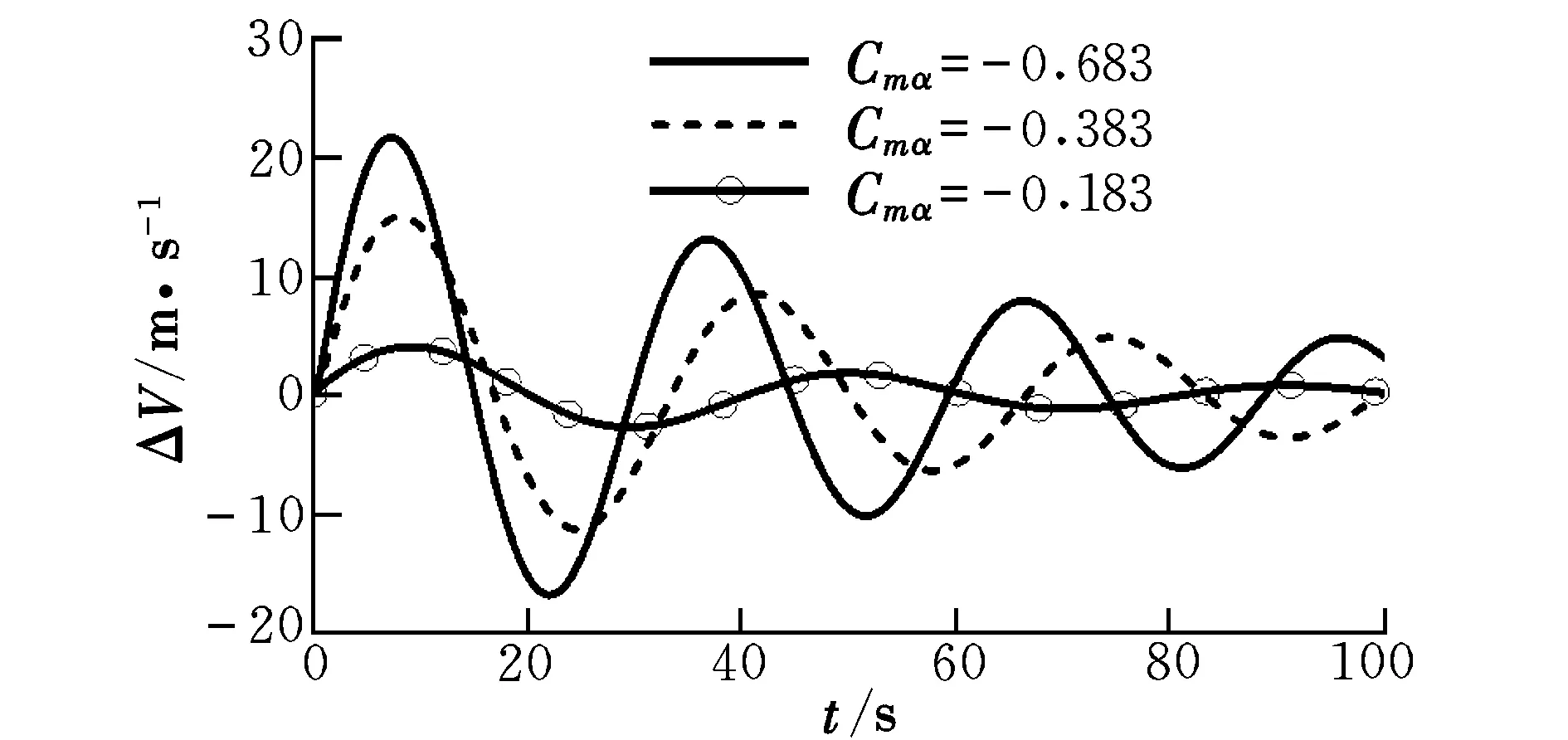
圖4　不同Cmα條件下的速度對比Fig.4　Comparison of velocities on different Cmα

3.1.2基于線性方程氣動力非線性的影響

當氣動力的非線性特征明顯時,必須建立非線性氣動力模型。考慮升力系數與俯仰力矩系數隨迎角的二次方非線性變化,構造了相應的非線性升力與非線性俯仰力矩模型,如式(6)～式(8)所示。

式(6)為針對CLα隨α不斷增大而增大構造的非線性升力數學模型。

(6)

式中:ε為非線性升力在全部升力中所占的比重,ε越大,非線性升力所占比重越大。ε分別取0,2,4,其中兩種特殊情況為ε=0和ε=4,分別表示升力完全用線性表示和非線性升力部分接近線性升力。下文中的ε含義相同,只是數值不同。

圖5給出了各個飛行參數在非線性升力條件下的時間響應曲線。

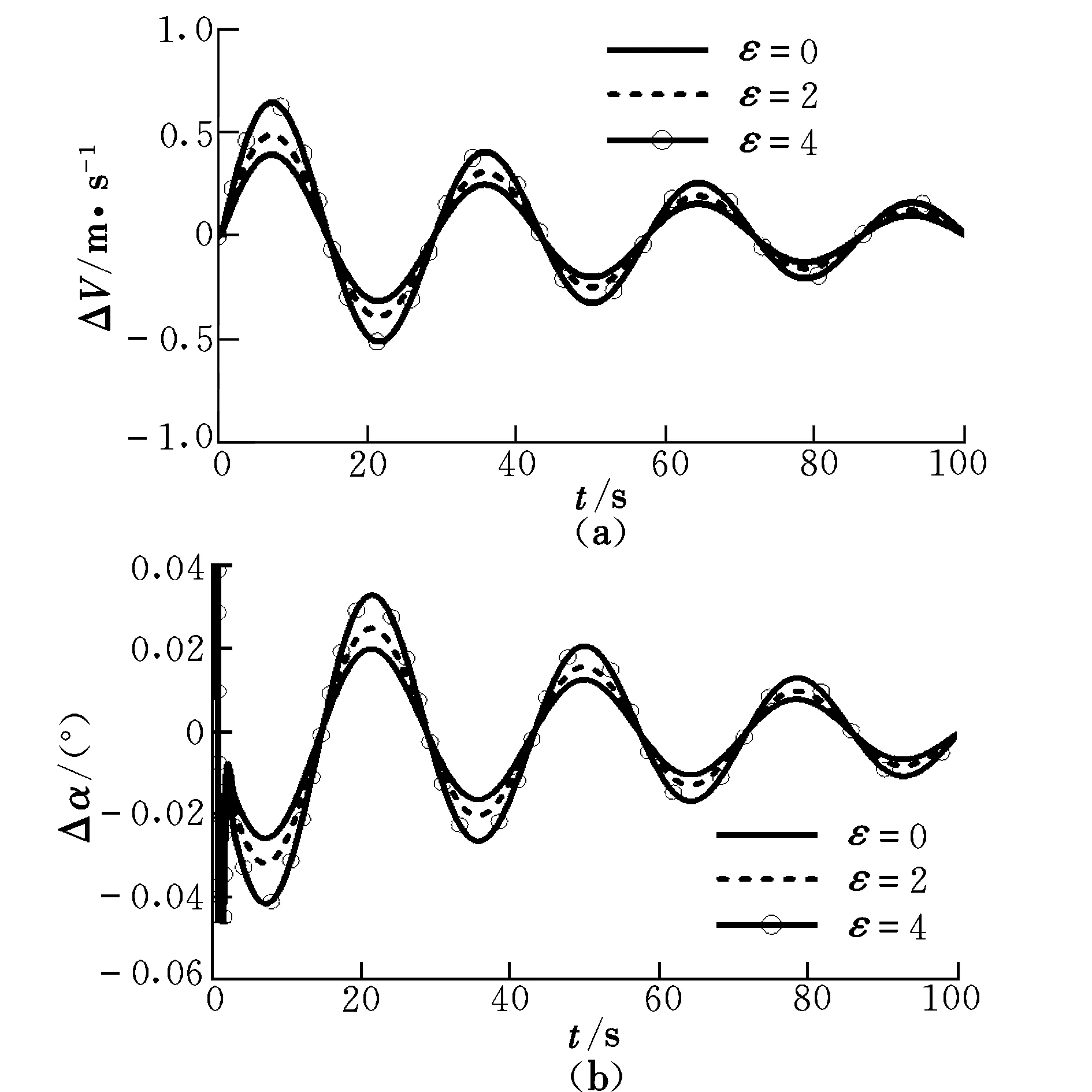
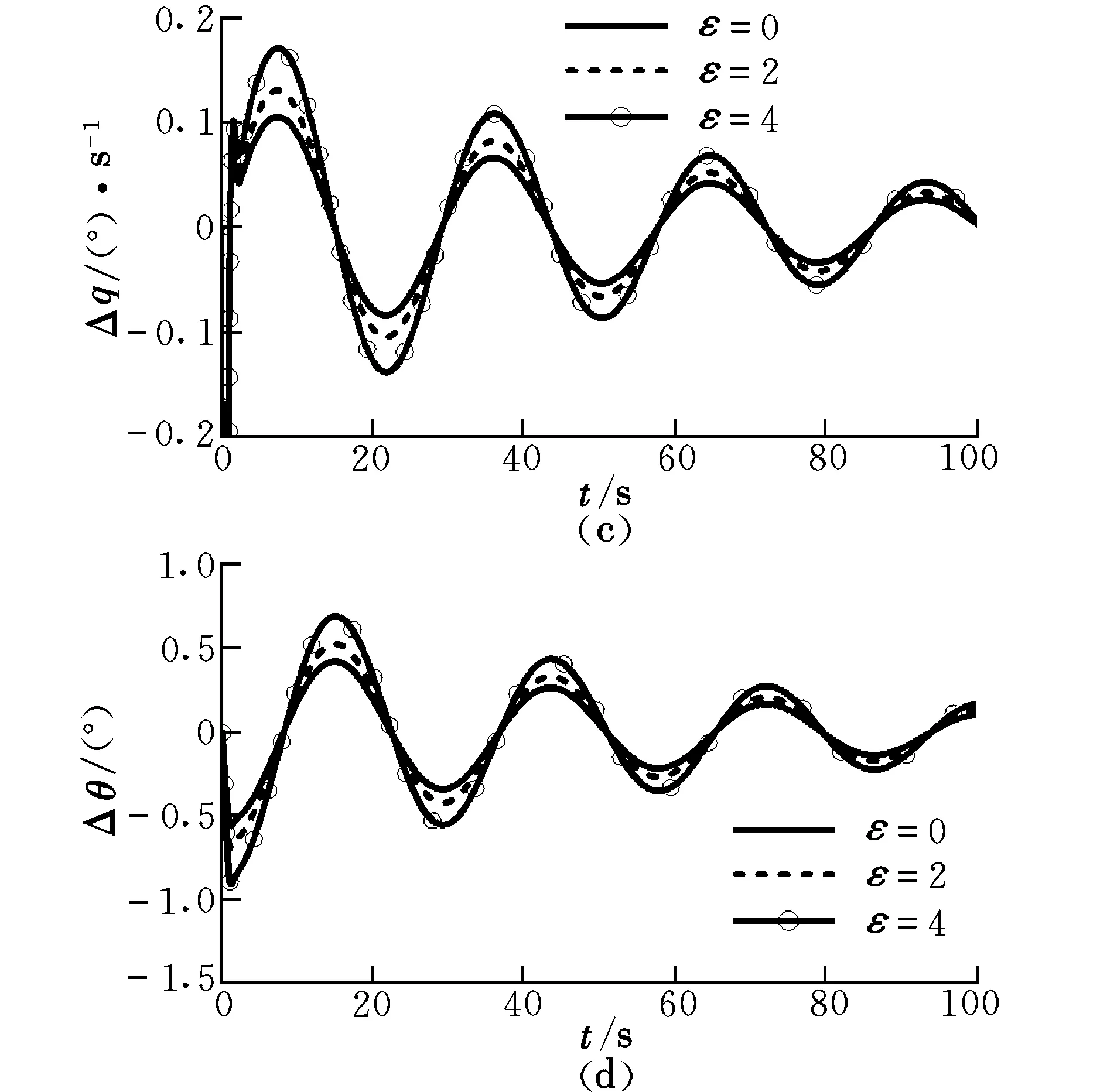
圖5　仿真結果(針對式(6))Fig.5　Simulation results(for formula(6))

從圖中可以看出,ΔV,Δα,Δq和Δθ的定性變化規律相同;非線性升力對周期幾乎沒有影響,而對幅值有一定的影響;隨著非線性升力的增大,幅值增大;當非線性量接近線性量時,ΔV,Δα,Δq和Δθ分別增大了約63.3%,64.4%,61.9%和63.0%。

式(7)為針對CLα隨α的增大而減小構造的非線性升力數學模型。

(7)

圖6為式(7)對應的數值仿真結果。從圖中可以看出,非線性升力對周期幾乎沒有影響,而對幅值有一定的影響。ε增大,周期不變,幅值減小。當非線性量接近線性量時,ΔV,Δα,Δq和Δθ分別減小了29.3%,29.3%,28.9%和29.2%。

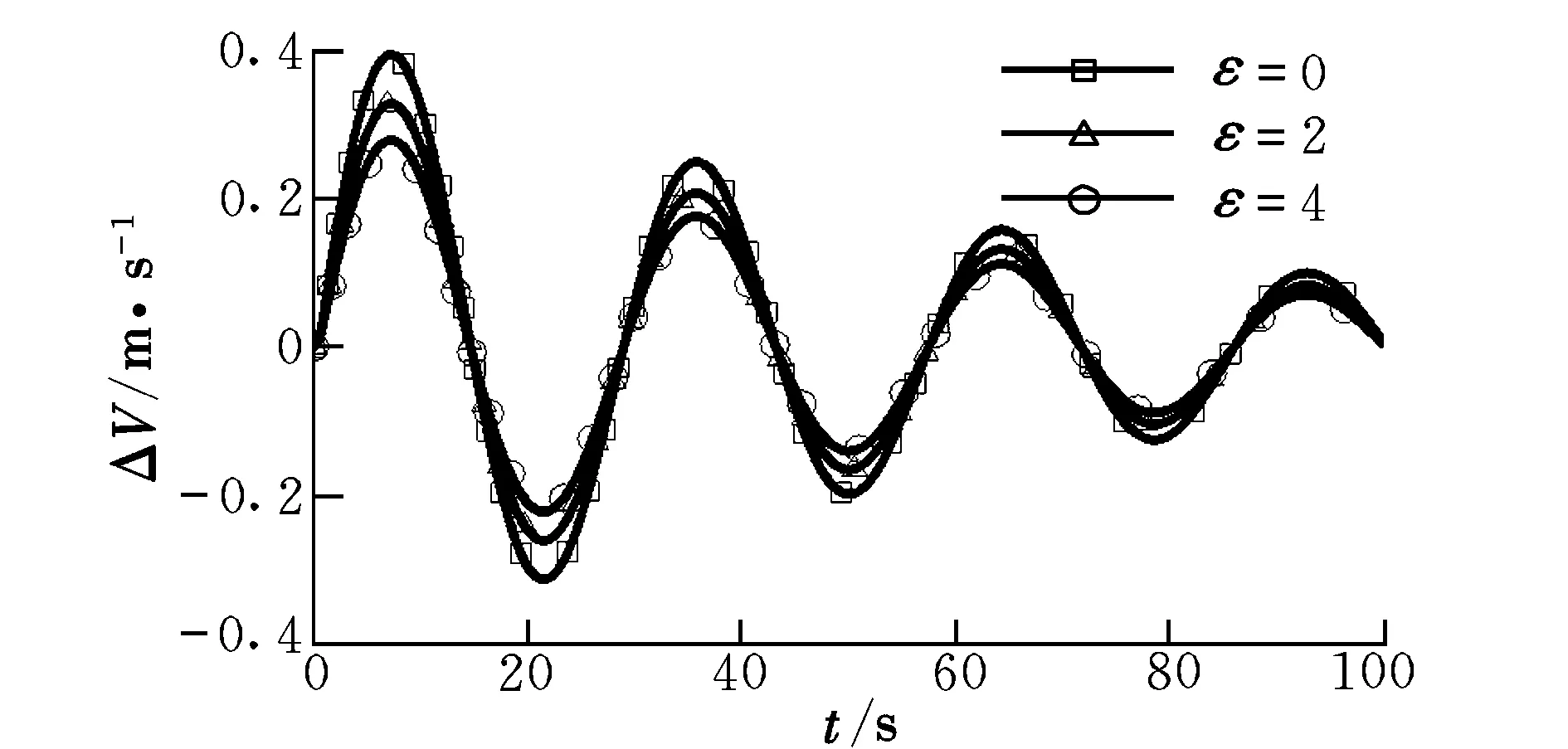
圖6　仿真結果(針對式(7))Fig.6　Simulation results(for formula(7))

式(8)為針對Cmα隨α的增大而增大構造的數學模型。

(8)

圖7為式(8)對應的數值仿真結果。由圖7可見,非線性俯仰力矩對周期也幾乎沒有影響,而對幅值有一定的影響。隨著非線性俯仰力矩的增大,幅值減小。當非線性量接近線性量時,ΔV,Δα,Δq和Δθ分別減小了50.8%,50.4%,50.7%和50.8%。

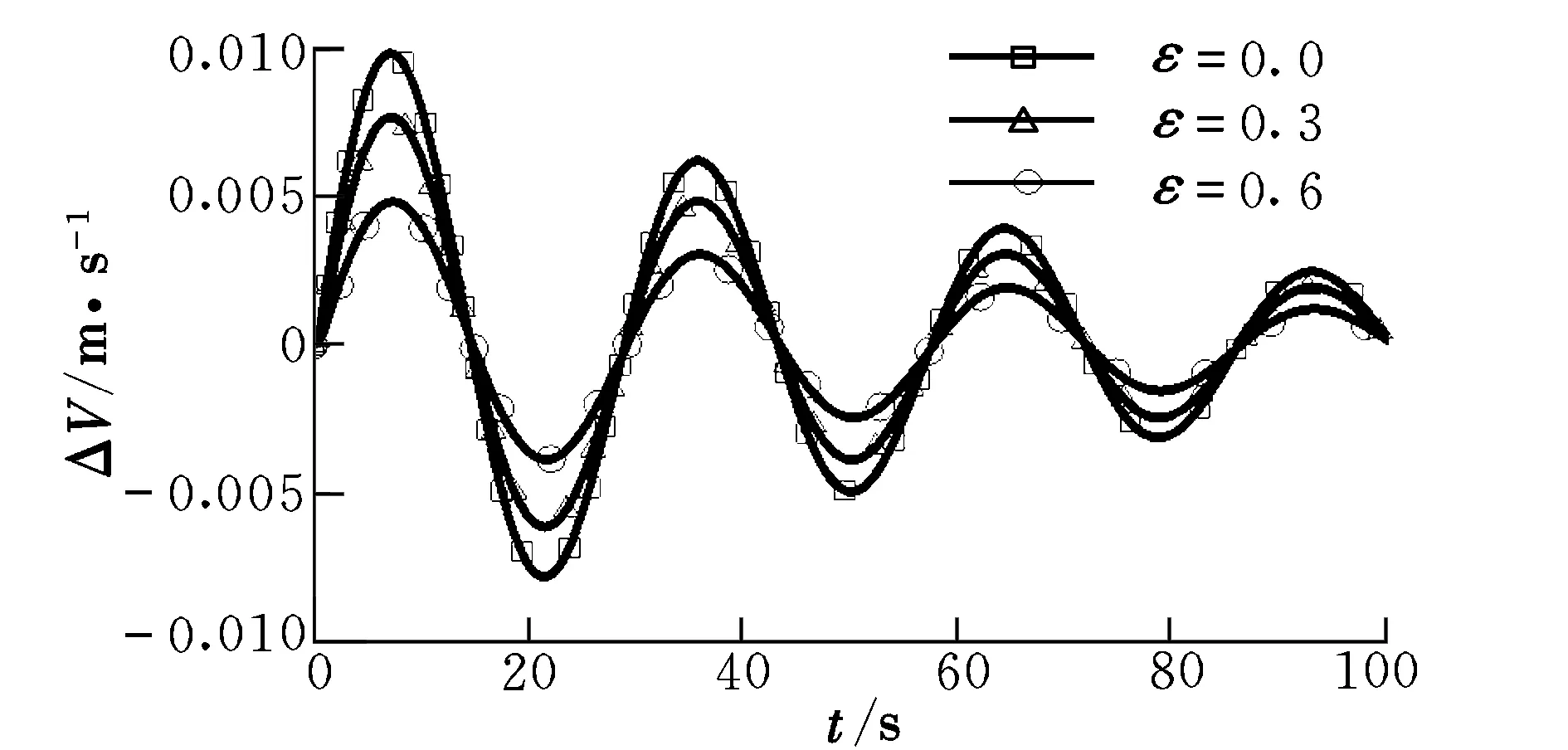
圖7　仿真結果(針對式(8))Fig.7　Simulation results(for formula(8))

3.1.3基于非線性方程氣動力非線性的影響

在非線性方程中,非線性氣動力不能再用增量表示,而應該采用狀態量。構造非線性氣動力模型如式(9)～式(11)所示。初始條件和時間間隔的設定值不變,直接對式(1)中的縱向非線性方程進行時間推進求解。

式(9)為針對CLα隨α的增大而不斷增大構造的非線性升力數學模型。

(9)

圖8為式(9)對應的數值仿真結果。從圖8中可以看出,在考慮非線性方程的基礎上,非線性升力對周期幾乎沒有影響,而對幅值有一定的影響。隨著非線性升力的增加,幅值增大。當非線性量接近線性量時,ΔV,Δα,Δq和Δθ分別增大了約8.26%,7.77%,8.10%和7.98%。

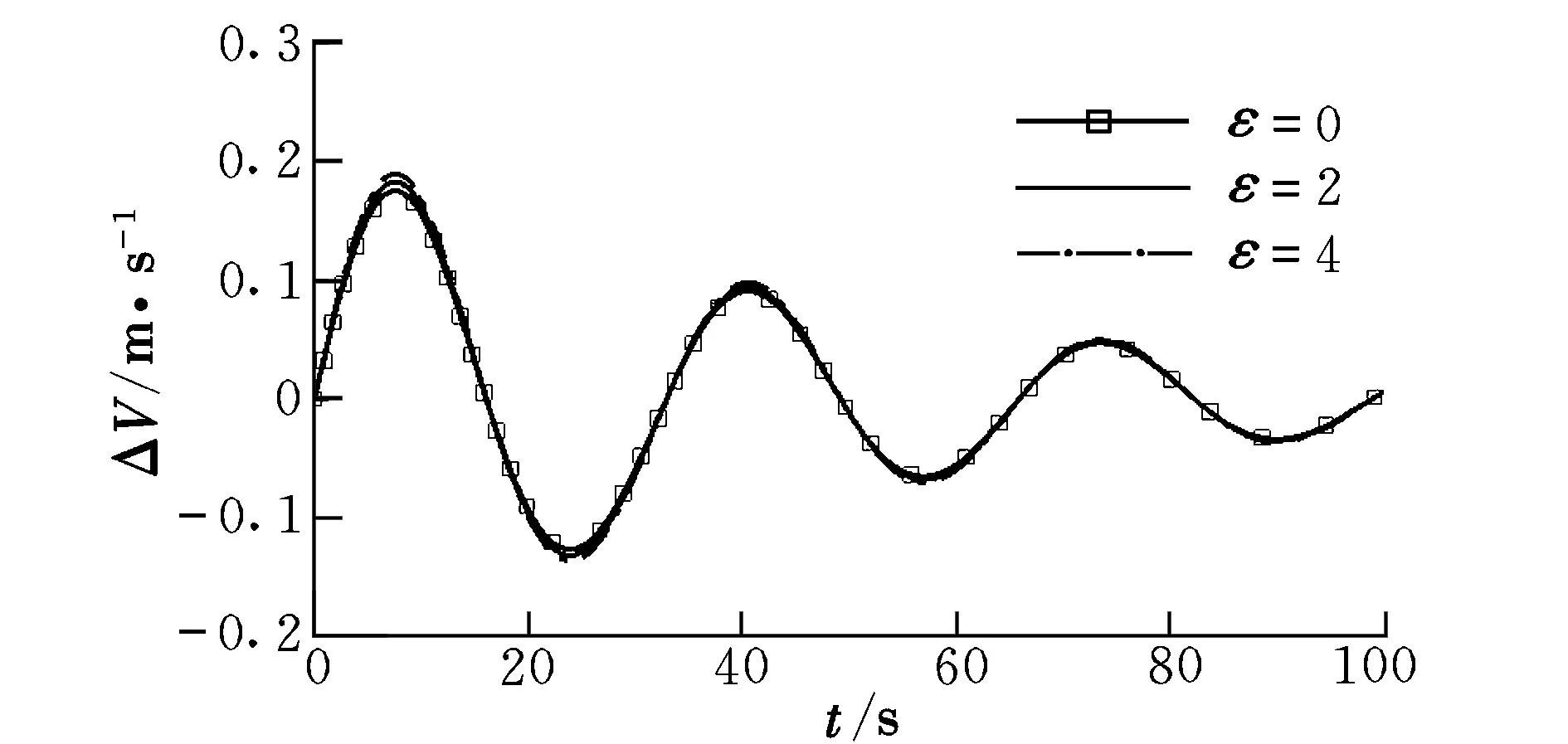
圖8　仿真結果(針對式(9))Fig.8　Simulation results(for formula (9))

式(10)為針對CLα隨α的增大而不斷減小構造的非線性升力數學模型。

(10)

圖9為式(10)對應的數值仿真結果。從圖9中可以看出,非線性升力對周期幾乎沒有影響,而對幅值有一定的影響。隨著非線性升力的增大,幅值減小。當非線性量接近線性量時,ΔV,Δα,Δq和Δθ分別減小了約9.64%,9.10%,9.77%和9.51%。

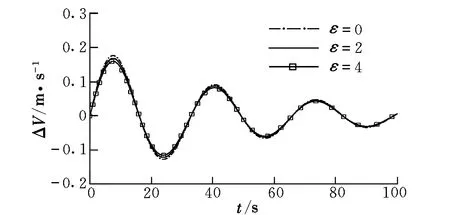
圖9　仿真結果(針對式(10))Fig.9　Simulation results(for formula(10))

式(11)為針對Cmα隨α增大而不斷增大構造的非線性俯仰力矩。

(11)

圖10為式(11) 對應的數值仿真結果。從圖10中可以看出,非線性俯仰力矩對周期幾乎沒有影響,而對幅值有一定的影響。隨著非線性俯仰力矩的增大,幅值增大。當非線性量接近線性量時,ΔV,Δα,Δq和Δθ分別增大了9.57%,7.77%,9.54%和9.19%。

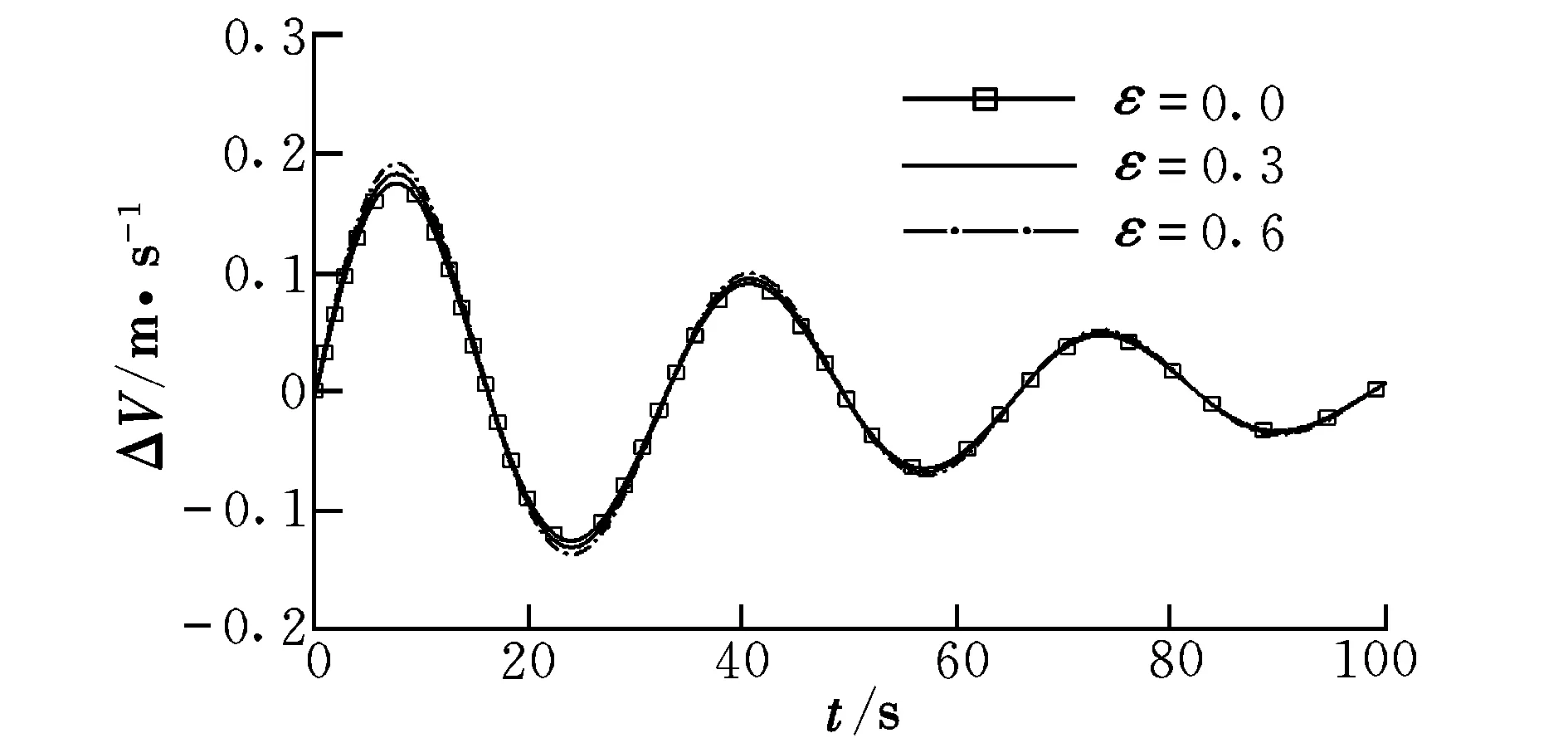
圖10　仿真結果(針對式(11))Fig.10　Simulation results(for formula(11))

從仿真結果可以看出,在非線性方程中考慮非線性氣動力的影響比在線性方程中考慮非線性氣動力的影響要小。

3.2方程非線性的影響

對文獻[8]中的一架FAR23運輸機進行穩定性分析,通過時間推進的數值方法對式(1)中的非線性方程進行求解并且只考慮縱向,氣動力模型采用線化數學模型,得到各個運動參數的時間歷程曲線,將其與小擾動線化理論得到的線性結果進行對比,如圖11所示。圖中,u,v分別為飛行器在機體軸系中沿Oxb,Ozb方向的速度分量。

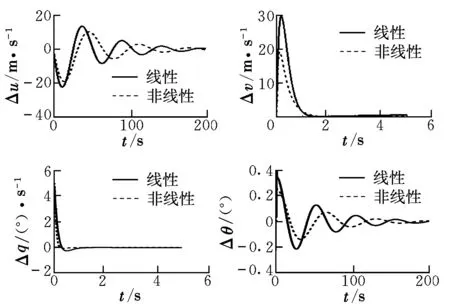
圖11　仿真結果的比較Fig.11　Comparison of simulation results

由圖11可見,考慮方程非線性的非線性動力學模型的穩定性與基于線性擾動運動模型的穩定性分析結果存在差異,具體表現為周期增大、幅值減小、衰減率增大。

4　結束語

本文系統地研究了飛行動力學非線性方程和非線性氣動力對飛行器縱向穩定性的影響,得到以下結論:

(1)方程的非線性引起幅值減小、周期增大、衰減率增大;

(2)CLα減小引起收斂速度變慢、振蕩周期變小、振蕩幅值增大;Cmα增大引起振蕩周期增大、振蕩幅值變小;

(3)氣動力的非線性對振蕩周期幾乎沒有影響，對幅值有影響,并且非線性氣動力在線性飛行動力學方程中的影響比在非線性方程中大。

從仿真結果來看,動力學模型中的非線性對飛行器穩定性影響較小,這與本文采用的算例以及簡化過程有很大的關系。對于非線性特征非常明顯而且耦合嚴重的高超聲速飛行器來說,即使小量的非線性也會對穩定性結果有較大影響。下一階段的工作將把這一研究思路與方法用于具體的高超聲速飛行器,并且考慮相互耦合的情況,具體研究非線性動力學模型對高超聲速飛行器穩定性的影響。

[1]陳予恕,郭虎倫,鐘順.高超聲速飛行器若干問題研究進展[J].飛航導彈,2009(8):26-33.

[2]Jason T P,Andrea S,Stephen Y,et al.Control-oriental modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance,Control,and Dynamics,2007,30(3):856-869.

[3]楊愛明,翁培奮.微型飛行器小展弦比機翼的低雷諾數氣動特性分析[J].空氣動力學報,2005,23(1):57-67.

[4]王延奎,單繼祥,田偉.聯翼布局俯仰力矩非線性變化特性的數值模擬[J].北京航空航天大學學報,2012,38(7):862-866.

[5]曾開春,向錦武.高超聲速飛行器飛行動力學特性不確定分析[J].航空學報,2013,34(4):798-808.

[6]賈區耀.天空飛行與地面風洞實驗動態氣動相關性研究[J].實驗流體力學,2006,20(4):87-93.

[7]方振平,陳萬春,張曙光.航空飛行器飛行動力學[M].北京:北京航空航天大學出版社,2010.

[8]Kasim Biber.Stability and control characteristics of a new FAR23 airplane[R].AIAA-2006-255,2006.

(編輯：姚妙慧)

Influence of longitudinal nonlinear dynamic model on stability of vehicle

YE Liu-qing, YE Zheng-yin

(National Key Laboratory of Aerodynamic Design and Research, NWPU, Xi’an 710072, China)

Stability analysis of aircraft is closely related to the dynamics analysis model, the traditional stability analysis method is to establish a linear model based on small disturbance assumption. When the nonlinear characteristics are very obvious in a flight state, people often care about how much effects the errors between the calculated value and the true value will bring. On the basis of establishing nonlinear flight dynamics model and nonlinear aerodynamic model, this paper uses the time marching method to study two nonlinear problems systematically. The results show that the cycle increases, the amplitude decreases and the attenuation increases when the model of nonlinear flight dynamics equation is compared with linear model. The results also show that the nonlinear aerodynamic force has no effect on the cycle,but a certain influence on amplitude.

nonlinear equation; nonlinear aerodynamic force; flight dynamics; stability

2015-11-17;

2016-04-28; 網絡出版時間:2016-04-29 08:32

葉柳青(1993-)，女，湖北黃岡人，碩士研究生，研究方向為飛行力學。

V212.12

A

1002-0853(2016)04-0019-05