基于熱力耦合的單磨粒臨界磨削仿真分析
吳書安,祝錫晶,郭策
(中北大學 機械與動力工程學院,太原 030051)
磨削加工是精密加工中一種重要的方法。在磨削加工的仿真研究中,單磨粒磨削作為砂輪磨削的一種簡化形式,近年來受到越來越多學者的重視[1—2]。SU等[3]采用自適應網格劃分技術,建立了一種粒尖為四凌錐切刃的單磨粒磨削模型。張明等[4]使用Deform-2D軟件建立單磨粒磨削平面仿真模型,分析了磨粒前角與磨削力和工件表面溫度之間的關系。在磨削中,材料的塑性去除能實現工件表面更低粗糙度和更好表面質量的要求[5]。BIFANO等[6]最早研究磨削過程的塑性加工臨界條件,認為當磨粒切削深度小于其臨界磨削深度時,可以實現脆性材料的塑性去除。言蘭等[7]通過數值仿真研究不同工藝參數下單磨粒耕犁和磨削的臨界磨削轉變過程,得到不同切削速度下的臨界轉變切削深度。磨削時由工件與磨粒接觸面摩擦產生的熱量會對磨削過程有一定的影響[8]。HUO等[9]對單磨粒實現硅材料的脆-塑轉變做了一定的研究,并分析了磨削熱對磨削過程的影響。
Ti6Al4V合金具有比強度高和疲勞強度高等良好性能,在航空航天發動機和醫療器械等方面得到廣泛應用。在這些應用場合,迫切需要運用更高表面質量和更低粗糙度的零部件。目前,尚未見針對Ti6Al4V合金材料受磨粒刃圓半徑和磨削深度共同作用下實現臨界磨削的研究。本文基于熱力耦合模型,針對單磨粒的不同刃圓半徑和磨削深度,對單磨粒實現材料的臨界磨削進行仿真研究。
1 仿真模型的建立
1.1 正交微磨削過程仿真
考慮磨粒整體形狀的不規則性[10],將磨粒頂尖簡化成圓錐角為2θ的圓錐體。磨削時,磨粒頂尖會被部分磨損。將其等效為帶有刃圓半徑為r的圓錐體,磨削深度為h,如圖1所示。
在磨削過程中,磨粒的圓錐角為30°。磨粒采用剛體模型并劃分三角形網格單元,網格劃分如圖2a所示。刃圓半徑r=0.1 μm和1 μm時,工件的幾何尺寸為 34 μm×10 μm,圓弧段半徑為 6 μm;刃圓半徑r=10 μm時,工件的幾何尺寸為340 μm×100 μm,圓弧段半徑為60 μm。對工件劃分四邊形網格單元,網格劃分如圖2b所示。工件模型的上邊和左右兩邊均采用密度偏離撒種,得到網格總單元數為4925,總結點數為5148。
微切削中,許多研究者用實驗證明:當材料變形尺寸減小到一定值時,有效流動應力發生顯著尺度效應的現象。運用應變梯度塑性理論建立的工件材料本構模型,能成功模擬該實驗現象。
考慮磨削時磨粒與工件接觸表面的熱傳遞,設置傳熱系數為0.9[11]。建立熱-力耦合的正交微磨削有限元模型,假設條件為[12]:磨粒的磨削瞬間被視為平面切削過程;磨削過程為穩態切削;磨削溫度不足以使材料有金相組織等變化;刀具被約束為剛體。
基于應變梯度塑性理論的材料有效流動應力計算公式為[12]:
式中:A、B、C、m、n、αC為材料系數,其中[13]C=0.014,m=0.466,n=0.71;G為剪切模量;b為伯格斯常量;分別為有效應變和有效應變率;η為有效應變梯度;σJC為用 Johnson-Cook模型計算的有效流動應力;T為量綱溫度項。
運用 ABAQUS/Explicit有限元軟件對正交微磨削過程進行仿真。約束工件其余三條邊x和y方向的位移自由度。給刀具設定一參考點,并添加運動速度約束,數值大小為60 m/min。微磨削摩擦模型采用罰函數摩擦模型,摩擦因數為 0.5。工件和磨粒材料參數如表1所示[14]。

表1 工件和磨粒材料參數Table1 Material parameters of workpiece and grain
1.2 條件模型的建立
材料在有效流動應力達到屈服極限之前發生彈性變形,無切屑產生;有效流動應力超過材料強度極限時開始有微裂紋產生,并發生塑-脆轉變。因此,針對Ti6Al4V合金材料塑性去除的條件模型為:σ≤δ0σs0,不產生切屑;δ0σs0<σ≤δ1σsm,塑性去除階段;δ1σsm<σ,脆性去除階段。其中,δ0為單磨粒磨削時塑性域系數,δ1為單磨粒磨削時脆性域系數[15]。具體確定均需要進行大量實驗數據分析統計。
2 結果分析
針對單元編號2476的有效流動應力和其右上角的節點編號2601的磨削溫度,分析這兩個變量受磨粒刃圓半徑和磨削深度的影響。單磨粒磨削仿真模型圖(圖3)中,有效流動應力沿磨粒頭周向分布,同一圓弧線上數值相同;離磨粒頭部圓弧面越遠,工件的有效流動應力越小。這驗證了吳繼華等[12]所得的結論。
改變單磨粒磨削深度h與刃圓半徑r的數值大小,仿真結果如圖4所示。圖4a、b、c為相同刃圓半徑下不同磨削深度對磨削的影響;圖4c、d為相同磨削深度下不同刃圓半徑對磨削的影響。
針對磨削時的臨界脆-塑轉變現象和熱效應,具體從以下三種條件分析切屑根部所取單元和節點的有效流動應力最大值(σmax)及磨削溫度最大值(Tmax)的變化情況。
1)r=0.1 μm。h取 6組數值,仿真得出σmax和Tmax,如表2所示。繪制折線圖,如圖5所示,σmax先增大后減小。擬合可得,當h≈0.17 μm時,σmax達到最大值,為1009.53 MPa,并出現了尺度效應所體現的“越小越強”現象。Tmax隨著h增大而近似呈線性增大。參考條件模型可得:工件材料基本處于脆性分裂階段。由表1可知,Ti6Al4V合金的強度極限σsm=923.2 MPa。擬合可得,在r=0.025 μm時,實際塑性去除的有效流動應力數值可能大于塑-脆轉變的臨界值δ1σsm。當h≈0.17 μm 時,磨削熱的熱軟化效應開始對切屑根部材料的有效流動應力產生主要影響。這是由于磨削溫度超過了Ti6Al4V合金的動態重結晶溫度[14],此時材料內部發生晶粒位錯的重新排布,阻礙切屑根部局部塑性變形的阻力下降,出現應力軟化現象。繼續增大h,由數據擬合可知,當h超過0.33 μm時,流動應力數值可能小于塑-脆轉變的臨界值δ1σsm,從而實現材料的脆-塑性臨界轉變。
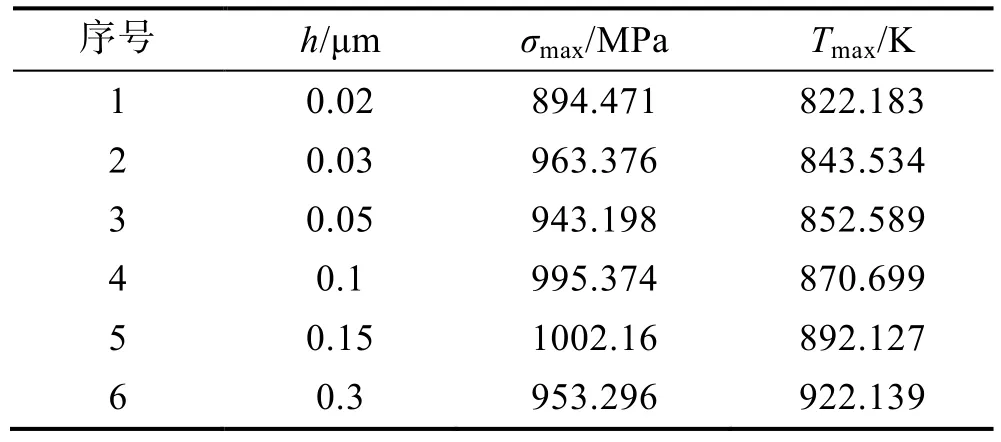
表2 各變量值(r=0.1 μm)Table2 Value of each variables (r=0.1 μm)
2)r=1 μm。h取 6組數值,仿真得出σmax和Tmax,如表3所示。繪制折線圖,如圖6所示。擬合可得,當h≈0.5 μm 時,σmax有最小值,為 948.479 MPa;繼續增大h,當h≈2.6 μm 時,σmax取得最大值,為998.176 MPa。熱軟化效應對σmax的影響不明顯。參考條件模型可得:切屑基本處于脆性分裂階段,這將引起工件表面鋸齒狀的形成,增加磨削過程對磨粒的震蕩沖擊,不利于工件表面質量的提高,并會降低磨粒的使用壽命。
3)r=10 μm。h取6組數值,仿真得出σmax和Tmax,如表4所示。繪制折線圖,如圖7所示。σmax隨著h的增大,先快速降低再減緩,繼續增大h會出現最小值。在h范圍內,最小有效流動應力為720.352 MPa,最大為763.59 MPa。而Tmax繼續增大,當超過Ti6Al4V合金的動態再結晶溫度后,晶粒位錯重排,出現的熱軟化效應促進σmax的進一步降低。參考條件模型可得:切屑的形成均處于塑性流動階段,這有利于減少磨粒的磨損。
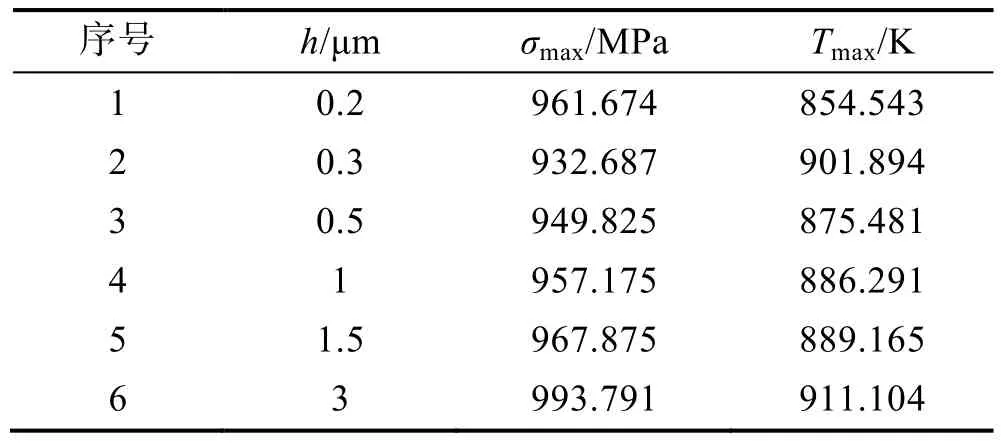
表3 各變量值(r=1 μm)Table3 Value of each variables (r=1 μm)
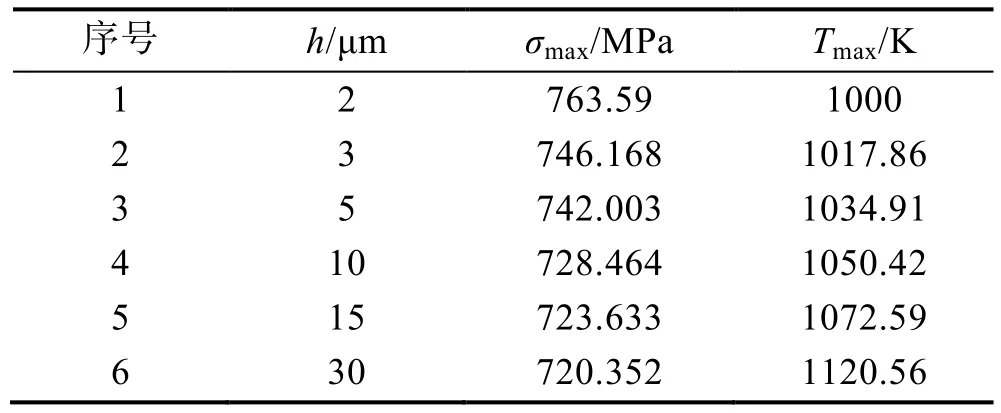
表4 各變量值(r=10 μm)Table 4 Value of each variables (r=10 μm)
對比可知,r對σmax的影響也會出現“越小越強”的現象。當r為0.1 μm時,改變h,會出現脆-塑性去除的臨界轉變值。當r為10 μm時,塑性去除的閾值范圍較寬。而r為1 μm時,所研究h范圍幾乎沒有塑性去除的臨界值出現。對比表3和表4最后一組數據可知,r增大也會強化磨削熱的產生。磨削Ti6Al4V合金時,應盡量避免使用r≈1 μm的磨粒;當r≈0.1 μm時,增加h,有利于高質量的表面形成;選用r≈10 μm時,可參考文中h的數據,適當增加h可以提升磨削效率。對比圖6和圖7可知,r尺寸取 1~10 μm范圍,磨粒刃圓半徑對工件材料實現脆、塑性切削的影響比磨削深度的影響更大。
3 結論
1)基于應變梯度塑性理論的 J-C材料本構模型,建立了考慮單磨粒刃圓半徑、磨削深度的切屑根部有效流動應力的熱-力耦合有限元分析模型。用該模型驗證了工件材料在微磨削時的尺度效應現象。
2)針對Ti6Al4V合金材料,當刃圓半徑為0.1 μm時,適當調整磨削深度,磨削過程可能出現脆-塑臨界轉變,進入塑性去除階段。當磨削深度為0.17 μm時,磨削熱的熱軟化效應開始對切屑根部材料的有效流動應力產生主要影響。當刃圓半徑為1 μm時,幾乎不出現材料塑性流動的現象,磨削時應注意避免。當刃圓半徑為10 μm時,磨削均處于條件模型中的塑性去除階段,其塑性去除域的范圍較寬,未出現臨界磨削現象,可繼續增加磨削深度以提高效率。
3)在微磨削下,磨粒刃圓半徑與磨削深度對材料切屑的形成有重要影響,但并非尺寸越小越好。當r為1~10 μm時,磨粒刃圓半徑對工件材料脆、塑性磨削的影響比磨削深度的影響更大。

