NTM焊點模型在白車身彎扭剛度分析中的應用
王力
(廣州汽車集團股份有限公司汽車工程研究院)
在汽車車身有限元分析中,焊點的模擬是一個重要的基礎課題。為了提升焊點模擬精度,分別出現了ACM和Fastener等焊點模型,這些模型由于出現較早,在焊點的模擬中存在較大誤差。文章研究了一種基于綁定接觸關系的焊點模型,稱之為NTM模型,采用該模型模擬焊點進行白車身彎扭剛度分析,發現可以獲得更高的精度,該焊點模型具有推廣價值。
1 ABAQUS常用焊點模型
ABAQUS是在汽車行業產品開發中廣泛使用的有限元程序。目前,基于ABAQUS的焊點模型主要有ACM和Fastener。ACM模型是在所焊接的面片單元(即模擬所焊接鈑金的兩層殼單元)之間建立一個六面體實體單元,實體單元的8個節點通過多點約束單元與面片單元的節點進行連接,從而實現焊接[1-2],這種模擬方式較少使用。Fastener焊點模型則是在面與面之間建立點對點連接來模擬焊點,首先在面片單元上建立結合點(fastener point);然后該連接點通過分布式耦合約束(distributingcouplingconstraint)與周圍的單元節點相連;最后通過一個CONNECTOR單元或者BEAM單元模擬焊核,并將面片上的2個結合點連接起來,從而構建焊點。
Fastener焊點模型的特點是焊核的2個節點都是通過分布式約束方程與面片的節點相連,與節點之間是一種約束的關系,相當于剛性單元直接將節點連接,從而導致模型的剛度較大,模型偏“硬”。為了解決模型偏硬的問題,研究了一種基于綁定接觸關系的焊點模型,這種模型的焊核由梁單元模擬,通過定義梁單元的截面使其與實際焊核截面一致,梁單元的2個節點分別通過綁定約束與面片單元建立接觸關系,實現兩層面片之間焊接。然后將這2種焊點模型應用于白車身彎扭剛度分析,將仿真分析結果與試驗結果進行對比,驗證了新焊點模型的分析精度,為白車身彎扭剛度仿真分析中焊點模擬的方法提供參考。
2 NTM焊點模型
該焊點模型不同于目前行業內使用的ACM和Fastener焊點模型。采用的梁單元(B31單元)模擬焊核,在梁單元的2個節點建立基于節點的接觸面,同時在所焊接的面片單元上建立基于單元的接觸面,然后定義梁單元節點與面片單元之間的“點-面”接觸關系為綁定約束(tie constraint),從而將兩層面片單元焊接在一起。對于這種焊點模型,將其命名為“節點綁定”焊點模型(node tie model),簡稱NTM模型。圖1示出NTM焊點模型的構造示意圖。
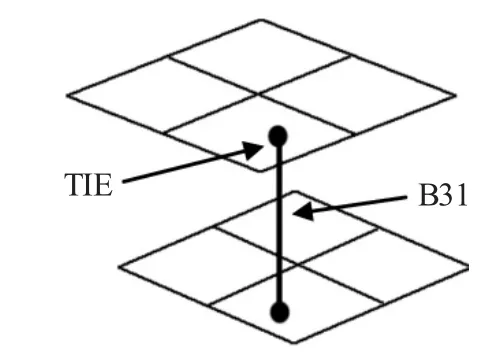
圖1 NTM焊點結構示意圖
圖2示出NTM焊點原理圖。NTM焊點的連接形式為“node to surface”,基本原理為:首先沿著B31單元的方向,在最近的殼單元上獲得1個投影點(project point);然后在投影點與B31單元的節點之間通過1個剛性梁單元(rigid beam)連接,從而將投影點的位移、力及力矩傳遞到B31單元的節點。B31單元節點A的投影點C與殼單元的4個節點(P1~P4)之間是采用多點約束方程關聯。其中ξ-η為殼單元局部坐標系,“rigid beam”為放大效果。由于C與A點之間采用剛性梁連接,在獲得C點位移、力及力矩后,很容易獲得B31單元的節點A相應的物理量。在殼單元局部坐標系中,C點的位移(uC)可以通過式(1)計算獲得:

式中:i=1,2,3,4;
αξi,αηi——多點約束方程中C對應于Pi點的加權系數;
uξi,uηi——殼單元節點Pi在局部坐標系中的位移。
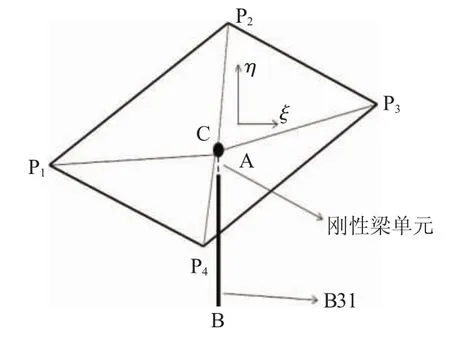
圖2 NTM焊點原理圖
同理,節點C載荷(FC)與力矩(MC)的計算公式為:
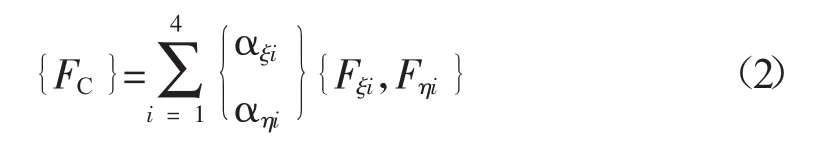
式中:Fξi,Fηi——殼單元節點Pi在局部坐標系中的力;
Mξi,Mηi——節點Pi在局部坐標系中的力矩。
3 NTM模擬焊點分析
3.1 雙帽型結構有限元分析
為了研究NTM模型模擬焊點精度和工程應用價值,將經典的“雙帽”型焊接結構作為研究對象。“雙帽型”焊接結構是通過2個沖壓成型的“帽型”鈑金拼合在一起,然后在連接的法蘭邊上采用點焊的方式將2塊鈑金拼合在一起,這種模型是研究焊點精度最常用的模型。
文章建立的雙帽型結構的有限元模型,如圖3所示。焊點分別采用CONN3D2和NTM的方式模擬,對比分析2種有限元模型的模態頻率和振型。然后,將有限元分析結果與試驗結果進行比對,分析NTM焊點模型在模擬焊點時的精度。

圖3 雙帽結構有限元模型
將2種焊點的有限元模型提交Nastran進行模態分析,分析結果和得到的模態振型,如表1、圖4和圖5所示。

表1 雙帽結構模態分析結果Hz


圖4 CONN3D2焊點模型模態振型

圖5 NTM焊點模型模態振型
對于雙帽型結構,很多學者進行了模態分析與試驗[3~4]。由于其是標準結構,因此可以借鑒相關的試驗結果用于文章的精度研究。比較有代表性的是文獻[3]中的試驗結果。
3.2 結果對比分析
采用統計學的方法分析2種焊點模型的精度,引入誤差函數[5],即標準差,用于評估焊點模擬的精度,其方程為:

式中:fi——第i階分析模態頻率;
Wi——第i階模態頻率的權重系數,全局模態,設Wi=2,局部模態,設Wi=1;
n——模態階數。
將表1中數據代入式(4),分別求得NTM與CONN3D2焊點模型的分析誤差分別為3.9%,9.9%。一般認為,分析的誤差在5%以內為較好的計算結果[6],可見NTM焊點的精度明顯高于CONN3D2焊點,具有較高的計算精度,有工程應用價值。
4 白車身彎扭剛度分析
4.1 白車身彎扭剛度分析方法
白車身的彎扭剛度表征了結構承載與變形的關系,是車身結構動力學設計的基礎[7]。
白車身彎曲剛度分析的加載點在前后排座椅上乘客重心位置。加載完成后,沿車身縱向測量各點的垂直位移,然后計算垂直位移最大點位置剛度值,此剛度值可作為白車身彎曲剛度性能的參考。
4.2 有限元分析與驗證
NTM焊點建模方式與傳統方式有所不同,因為其構造方式為B31單元,并通過綁定約束來建立焊接關系,這種構造方式就決定了NTM焊點的建模過程相對比較復雜。特別是對于有數千焊點的白車身而言,必須有足夠高效的焊點生成方法。為此,研究了NTM焊點快速生成方法的流程,如圖6所示。
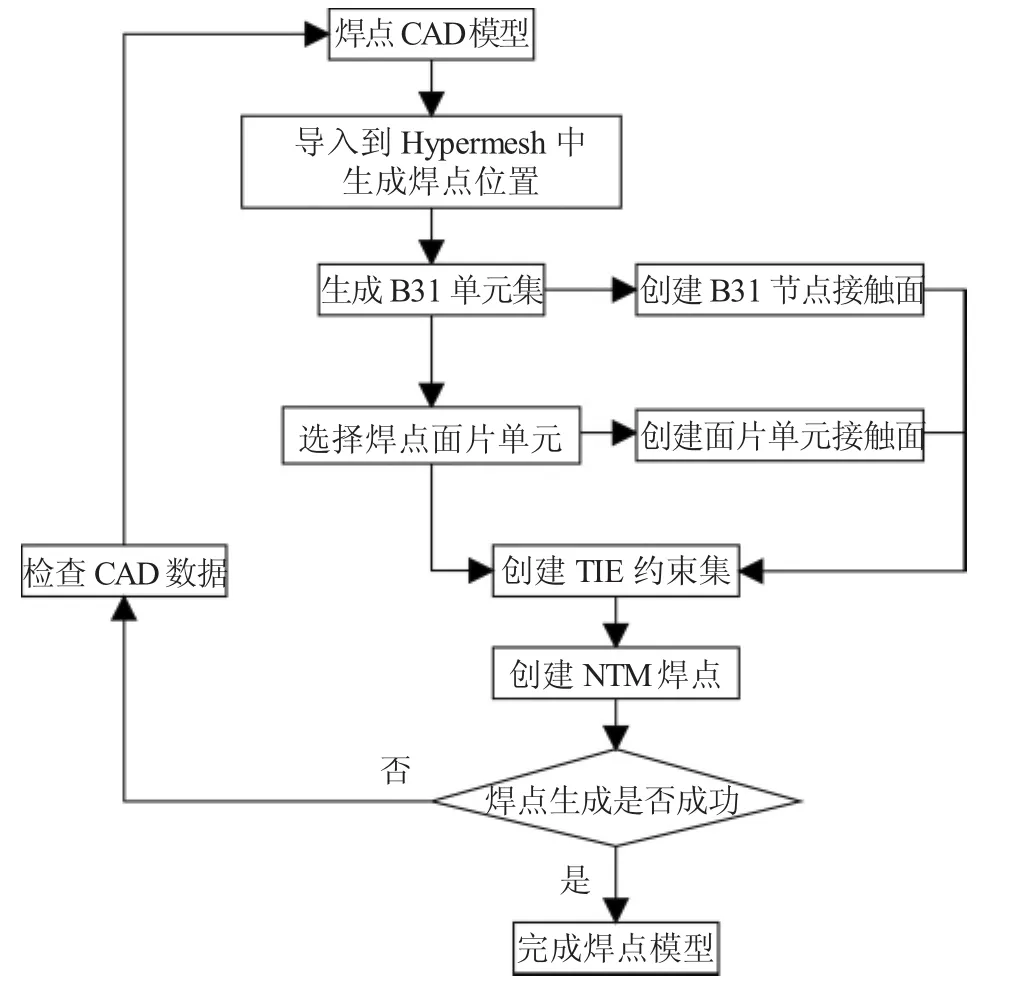
圖6 NTM焊點建模流程圖
NTM焊點建模的關鍵是必須定義2個集合:面片單元集合與B31節點集合。首先應將B31單元的所有節點歸集到節點集合,然后是“選擇面片單元”這一程序。在這個過程中必須將與焊核B31單元2個節點焊接的面片單元單獨選擇出來(如圖7所示),將無關的單元隱藏,創建面片單元集合,然后一次將所有面片單元與B31單元的節點建立接觸面。根據所建立的接觸面與B31單元的接觸點之間定義綁定約束,實現焊點建模,數千焊點可一次生成。效率與ACM和CONN3D2等焊點方式接近,具有很強的適用性。

圖7 面片選擇示意圖
以某A級轎車的白車身為例,首先建立白車身ABAQUS有限元模型,鈑金件采用殼單元劃分網格,單元類型為S4和S3。整個模型殼單元規模為59萬個,節點61萬個,其中三角形單元占整個單元比例為4.9%,如圖8所示。

圖8 白車身有限元模型
根據前述分析方法,將所建立的白車身有限元模型進行彎扭剛度分析,焊點分別采用CONN3D2和NTM焊點模型模擬,并將得到的分析結果與試驗結果進行比較。分析結果采用歸一化處理,將試驗結果設定為基準1,仿真計算結果與試驗結果進行比較,得到一個比值。該數值與1越接近,則表明計算結果與試驗結果越接近,計算精度越高,反之亦然。表2示出白車身彎扭剛度仿真分析與試驗值的對比。
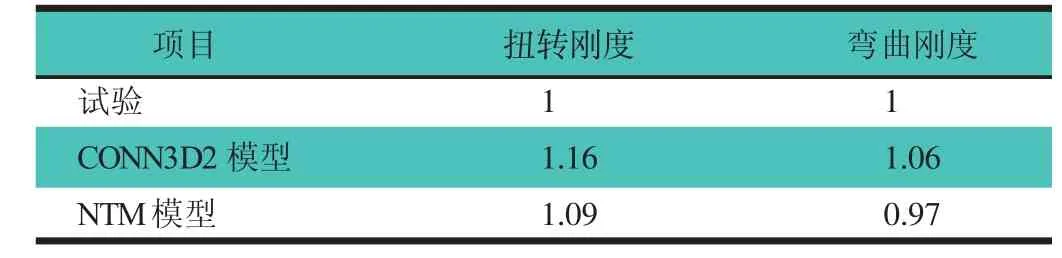
表2 白車身彎扭剛度仿真分析與試驗結果對比
從表2可知:在分析扭轉剛度時,2種焊點模型的有限元計算結果與試驗結果的誤差范圍均超過5%。CONN3D2模型的誤差較大,達到16%,其精度超過工程認可的范圍,有待提升,NTM焊點模型的誤差在10%以內,其精度在工程設計上可接受。在分析彎曲剛度時,兩者的誤差均優于扭轉剛度,NTM模型的誤差低于5%,具有很高的精度;而且,CONN3D2模型的彎扭剛度分析結果均比NTM模型絕對值更大,即剛度大,進一步證明CONN3D2焊點偏硬。綜合評價,NTM焊點的分析精度高于CONN3D2焊點。
5 結論
NTM焊點模型是一種基于綁定約束的焊點模型,可以定義焊核直徑與實際焊核結構更接近。在白車身彎曲剛度分析中,NTM可以獲得95%以內的計算精度,在扭轉剛度分析中的精度也在90%,均高于CONN3D2焊點模型。在彎扭剛度分析中,推薦使用NTM焊點模型。文章僅涉及NTM焊點的原理和計算精度,關于易用性未涉及,有待于進一步總結研究。

