“冪的運算”易錯題解析

李遙遙

?

“冪的運算”易錯題解析

李遙遙

話說唐僧師徒四人取經歸來，八戒一改好吃懶做的作風，重拾課本，美其名曰為跟上時代前進的腳步，做一個與時俱進的“豬”.這不，八戒被“冪的運算”中的眾多法則折磨得沒了豬樣，決定放下臉面前去花果山請教猴哥.悟空明了八戒來意后，拍著胸脯對八戒說：“呆子，莫急，看俺老孫的！”

悟空強調做此類題目時需明確性質的條件和結論，計算過程中還需注意符號.如：

例1計算：

【解析】應先把底數分別是a，-a的冪化成同底數的冪，才能應用同底數冪的乘法的性質.

【解析】①把（a-b）作為一個整體看做底數，②其中（b-a）4=（a-b）4，就可以根據同底數冪的乘法性質來求解.

例2計算：

【解析】運算中包括冪的乘方，同底數冪的乘法，最后合并同類項.

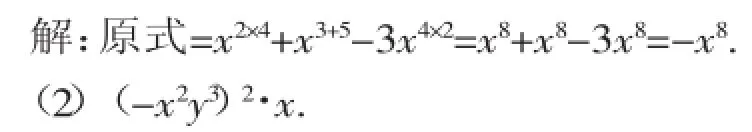
【解析】把-x2y3看作是-1，x2，y3的積，此時需注意系數及系數的符號，這里的-1不可忽略.

例3計算：

【解析】注意a的指數是1，本題根據同底數冪的除法即可直接解決.

解：原式=a7-3-1=a3.

【解析】利用同底數冪的除法性質進行運算時關鍵要找準底數和指數，底數可以是2x，也可以是-2x.

【解析】此題需注意：①任何一個非零數的零次冪等于1，即a0=1的前提是（a≠0）；

解：原式=-4+4×1-4=-4.

例5已知am=2，an=3，則a2m+n的值是多少？

【解析】此題遇到的冪的指數是和的形式，則需逆用同底數冪的乘法性質；碰到冪的指數是積的形式，則逆用冪的乘方的性質，即a2m+n=a2m·an，而a2m=（am）2.

當am=2，an=3時，

在悟空的指點下，八戒總算是掌握了本章的計算要領，當然八戒還悟出一個道理來：做題要細心，切勿馬虎、粗心.

（作者單位：新疆昭蘇縣育英學校）