傅立葉變換在數字信號處理中的應用研究

司新新 李佳

【摘要】 傳統的信號分析和處理使用了傅立葉變換，這種數學工具可以處理非平穩信號的分析局限問題，有著非常重要的意義。本文立足于相關的理論基礎，重點探討了短時傅立葉變換的實現情況以及窗函數的選取，希望為后期的相關應用研究提供參考和建議。

【關鍵詞】 不確定性原理 矩形窗 平移卷積 FFT

一、理論基礎

作為一種傳統數學工具，傅立葉變換在信號分析與處理方面有著較為重要的作用。傅立葉變換投入使用之后，就可以實現信號的時域和頻域之間的自由變換[1]。有些確定信號的頻譜并不會隨著時間變化，還有一些平穩的隨機信號，這些信號只要樣本選取的較為合理，就會通過傅立葉的相關分析在滿足一定條件后得到合適的結果。本文主要是立足于數字信號處理過程中，短時傅立葉變換是如何發揮作用的，最后使用Matlab 語言編程來了解相關的分析結果。

二、短時傅立葉變換的實現

（1）連續短時傅立葉變換的定義

假設：x（t）代表被分析信號，t=- ∞～∞，分析窗為w（t），那么就可以使用以下公式來解釋非平穩信號x（t）的短時傅立葉變換。即：

時間t 處短時傅立葉變換的計算也是按照了一個完整的過程展開的，具體情況如下：

1）獲取w（τ-t）。把分析窗w（τ）由時間零處平移至時間t 的位置上，得到需要的結果；2）獲取短時信號xi（τ）=x（τ）w（τ-t）。用水平方向移動過后的分析窗加窗截斷相關的信號，獲取需要的結果；3）分析結果。使用傅立葉變換分析短時信號xi（τ）的頻譜。在這個過程當中，相關環節的實際需求是較為明顯的，只要按照流程進行，就能得到相應的結果。如果，想要獲取高分辨率，那么在分析窗的選擇上要嚴格一些，時間短的分析窗比較符合標準。

（2）連續短時傅立葉變換的頻域形式

傅立葉變換有著自己獨特的性質，那么，兩個時域信號乘積的傅立葉變換與各自頻域的卷積相等，根據這個原理，（1）式也可以得到以下的結果：

式中窗函數在整個公式中有著自己獨特的存在價值，主要是為了實現x（n）在n 時刻附近的一小段信號的處理，這種處理也是由傅立葉變換來完成的。窗函數的變化與n之間是相輔相成的，前者隨著后者移動，從這個方面就可以得到相關的結論：信號頻譜隨著時間n的變化而變化。

2）從線性濾波的角度解釋離散短時傅立葉變換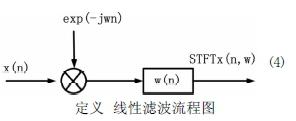

（4）短時傅立葉變換的時域、頻域采樣

短時傅立葉變換的ω作為一個變量，屬于連續性的，在計算機開展相關的運算的時候，頻域之間應該是離散化的。如果按照上述的解釋，那么選取的所有的參數必須符合相關的頻率采樣定理。在窗口的位置上，每次移動的距離應該都是一樣的，設定的數值為30。這就是一個與采樣有關的問題。短時傅立葉變換的時間分辨率是非常有限的，因此，在選樣方面要掌握好一個度，不然沒法滿足相應的需求，同樣，采樣的間隔也是要設置合理的。

三、窗函數的選取

1）不同的窗的選擇。不同的窗有著各自獨特的特點，因此應該按照實際的需求選擇合適的窗。矩形窗主瓣寬度較窄，旁瓣峰值較大，旁瓣峰值衰減速度較慢，這些屬性導致其容易泄露頻譜，從而導致分析性能的弱化。漢寧窗和海明窗有著與矩形窗截然相反的屬性，比較適合分析，因此，使用相關的分析方式時，能夠取得較為優異的分析結果。實際上，最佳的分析窗正好是上面兩者的結合，因此，在很多時候，具體的操作都是結合不同條件來選取最合適的分析窗函數的。2）不同的窗長度的選擇。當分析窗函數確定了之后，也應該注意選擇合適的分析窗長度。當窗口過于長的時候，信號不是很平穩的話，那么傅立葉變換的價值就會較小，運算量就會很大；相反，窗口過小，那么攝取的信息量又會太小。因此，要想獲取精確的結果，務必要選擇合適的窗函數的長度。

結束語：傅立葉變換在分析時變信號和非平穩信號方面有著自己的局限，而短時傅立葉則剛好可以解決這些問題，但是也并非沒有任何缺陷。另外，窗函數的長度也是必須要合適的，這樣才能確保短時信號處于較為穩定的狀態，進而得到比較精確的分析結果。

參 考 文 獻

[1]王金嬋，趙永安.分數傅立葉變換的進展與展望[J].應用光學，2003（5）：57.

[2]朱全銀，鄧建平.基于分數階傅里葉變換的線性調頻干擾抑制[J].探測與控制學報，2009（1）：1014.

[3]竇德召，常鴻森，林睿.變形分數傅立葉變換相關器[J].華南師范大學學報：自然科學版，2005（3）：7079.