探討中藥內(nèi)服并浸泡對糖尿病足的治療作用
單鋒波,高麗麗
(1.日照市東港區(qū)后村中心衛(wèi)生院,山東日照 276800;2.日照市東港區(qū)西湖鎮(zhèn)衛(wèi)生院,山東日照 276800)
糖尿病足是由于糖尿病引起的下肢周圍神經(jīng)與血管病變引起的足部感染、潰瘍或深部組織損壞。糖尿病足患者由于免疫力下降,容易出現(xiàn)感染的情況,而感染又加重了患者的病情,形成了惡性循環(huán),并最終導致截肢甚至死亡的結局出現(xiàn)[1]。近些年來,隨著我國糖尿病患者數(shù)量的增長,糖尿病足的發(fā)生率也不斷升高,該病具有發(fā)病復雜、治療周期長、致殘率致死率高的特點。因此,糖尿病足的臨床治療成為現(xiàn)代醫(yī)學關注的重要課題之一[2]。抗感染治療是糖尿病臨床治療的重要措施,但是抗生素的應用可能導致耐藥菌的產(chǎn)生,影響了抗生素的藥效,從而導致截肢率升高。中醫(yī)作為我國的傳統(tǒng)醫(yī)學,對于糖尿病足有著豐富的認識與治療經(jīng)驗。該病在中醫(yī)中歸屬于“脫疽”的范疇,且由于患者主要癥狀為下肢紅腫疼痛、膿性分泌物等,在中醫(yī)中屬于“熱毒”,采取辨證施治的方式能夠達到較好的效果[3]。該次研究為了進一步分析中醫(yī)藥治療效果,文章選選取2018年2月—2019年6月于該院收治的141例糖尿病足患者作為研究對象,研究如下。
1 資料與方法
1.1 一般資料
選取于該院收治的141例糖尿病足患者作為研究對象,隨機分為觀察組(70例)與對照組(71例)。觀察組70例患者中有男性患者39例,女性患者31例;年齡為 56~82 歲,平均年齡為(65.1±6.3)歲;病程為 5個月~6年,平均病程為(1.5±0.4)年。對照組 71例患者中有男性患者40例,女性患者31例;年齡為58~80歲,平均年齡為(66.8±5.6)歲;病程為 6 個月~7 年,平均病程為(1.6±0.7)年。兩組患者在一般資料方面的比較差異無統(tǒng)計學意義(P>0.05),具有可比性。
1.2 方法
對照組采取治療措施,主要是采取控制血糖、抗感染、手術清創(chuàng)、創(chuàng)面換藥以及對癥支持等治療措施。
觀察組則在對照組基礎上加入中醫(yī)治療方案,內(nèi)服四妙勇安湯,配方為:甘草、當歸10 g,玄參20 g,金銀花30 g,陰陽兩虛證加用太子參、黃芪、當歸,加水煎服,1劑/d,分早晚兩次服用;外用渴疽洗方浸泡,配方為大黃15 g,烏梅20 g,五倍子 30 g,加水煎煮至 500 mL,水溫控制在 37℃~40℃,1次/d,每次浸泡30~40 min。
1.3 觀察指標
觀察兩組患者的臨床療效以及治療后足背動脈內(nèi)徑以及血流量的差異[4-5]。該次研究療效平均標準:顯效:局部炎癥穩(wěn)定且壞疽組織截裁后無明顯疼痛,創(chuàng)面肉芽生長速度快,周圍皮膚溫度正常,保足成功;有效:局部炎癥穩(wěn)定且壞疽組織截裁后疼痛癥狀緩解,創(chuàng)面分泌物減少,周圍皮膚紅腫改善,保足基本成功;無效:局部炎癥不穩(wěn)定無法達到壞疽截裁標準,是否能夠保足有待繼續(xù)觀察。
1.4 統(tǒng)計方法
采用SPSS 16.0統(tǒng)計學軟件進行統(tǒng)計學分析,計量資料用(±s)表示,組間差異、組內(nèi)差異采用t值檢驗,計數(shù)資料比較采用χ2值檢驗,用百分率表示,P<0.05為差異有統(tǒng)計學意義。
2 結果
2.1 兩組患者的臨床療效
經(jīng)過治療后,觀察組患者臨床療效明顯高于對照組,差異有統(tǒng)計學意義(P<0.05),具體如表1所示。

表1 兩組患者的臨床療效
2.2 兩組患者治療后足背動脈內(nèi)徑與血流量
經(jīng)過治療后,觀察組患者治療后足背動脈內(nèi)徑與血流量均明顯高于對照組,差異有統(tǒng)計學意義(P<0.05),具體如表2所示。
表2 兩組患者治療后足背動脈內(nèi)徑與血流量(±s)
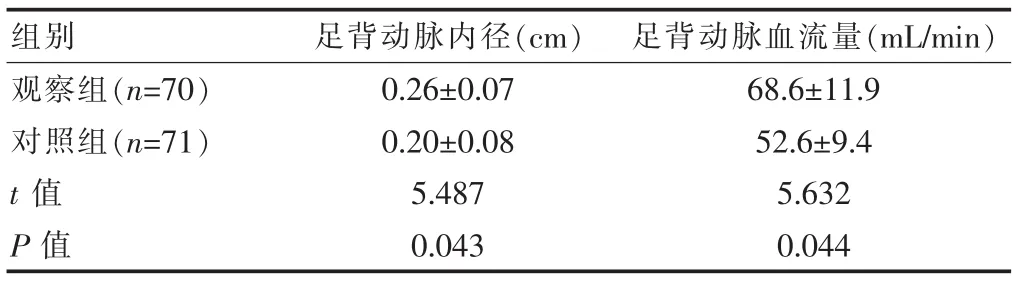
表2 兩組患者治療后足背動脈內(nèi)徑與血流量(±s)
組別 足背動脈內(nèi)徑(cm) 足背動脈血流量(mL/min)觀察組(n=70)對照組(n=71)t值P值0.26±0.07 0.20±0.08 5.487 0.043 68.6±11.9 52.6±9.4 5.632 0.044
3 討論
臨床醫(yī)學認為糖尿病足主要是由于糖尿病引起的神經(jīng)和微血管病變所致,神經(jīng)病變表現(xiàn)為患者足部皮膚干裂,容易受微生物侵襲,加上運動神經(jīng)病變導致行走姿勢異常而容易出現(xiàn)創(chuàng)面,創(chuàng)面愈合需要足夠的血供,但是血管病變的出現(xiàn)為病原微生物繁殖提供了良好環(huán)境[6]。總而言之,神經(jīng)病變、糖代謝異常、血流動力學異常是引起該病的主要原因。感染發(fā)生后導致大量炎癥因子激活,而胰島素作為人體重要的抗炎因子,糖尿病患者由于普遍存在胰島素表達水平低或胰島素功能障礙的問題,導致自身抗炎作用減弱,容易出現(xiàn)全身炎癥反應綜合征。若不及時控制感染,可導致病情加重惡化,最終出現(xiàn)截肢甚至死亡結局[7]。目前臨床對于糖尿病足主要是在積極控制血糖基礎上給予抗感染、清創(chuàng)、換藥及對癥干預措施,但是總體效果不夠理想,仍存在較高的截肢率和死亡率。因此需要盡早尋找更加有效的治療方案。
中醫(yī)中沒有糖尿病足這一病名,主要是根據(jù)該病的癥狀和表現(xiàn)將其歸納至“脫疽”“壞疽”的范疇,該病具有本虛標實之征,氣瘀血虛是該病的重要機制。目前中醫(yī)對于該病的治療主要是采取活血化瘀的治療方案[8]。氣血不足、飲食不節(jié)、情志失調(diào)、時感外邪以及勞累過度都可造成熱毒,因此該次研究中采取了清熱解毒、活血化瘀的治療方案[9]。四妙勇安湯來自《神醫(yī)秘傳》,方中的金銀花為君藥,具有清熱解毒、消腫散癰的功效,玄參為臣藥,具有清熱瀉火的功效,當歸為佐藥,具有溫通經(jīng)絡、活血止血的效果,甘草能夠調(diào)和諸藥,同時具有清熱解毒的效果,為使藥。全方具有清熱解毒、活血止痛的效果,是治療熱毒脫疽的妙方。現(xiàn)代藥理學指出,金銀花具有抗炎、抗病毒、抗細菌的作用,能夠加速炎癥因子的消退,從而提高機體的免疫力[10]。玄參具有鎮(zhèn)痛的作用,能夠擴血管、抗血小板聚集,從而改善局部微循環(huán)。當歸中含有多種生物活性物質(zhì),具有抗炎、鎮(zhèn)痛的作用。甘草是中藥材中使用最廣泛的藥物,具有抗炎、抗氧化的作用,能夠改善機體免疫力。渴疽洗方中的大黃具有寫清熱解毒、祛瘀瀉下的功效,烏梅具有較好的收斂作用,外敷能夠去瘡毒,五倍子具有消腫解毒的功效,全方具有消腫瀉熱的功效。現(xiàn)代藥理學證實大黃對多種細菌、病毒和真菌具有較好的抑制效果。五倍子中含有沒食子酸,具有抑菌效果[11]。該次研究中,觀察組在臨床療效以及治療后足背動脈內(nèi)徑以及血流量等方面均明顯高于對照組,差異有統(tǒng)計學意義(P<0.05),這說明在常規(guī)治療基礎上加入中醫(yī)內(nèi)服和中藥浸泡能夠有效提高糖尿病足的臨床療效,從而改善患者的生活質(zhì)量。
綜上所述,中醫(yī)藥內(nèi)服、沐足能夠有效提高糖尿病足的療效,且具有操作簡單的優(yōu)勢,可在臨床推廣使用。

