三線圈ICPT系統中繼線圈的位置優化

孫　躍　李云濤　葉兆虹　戴　欣（1.輸配電裝備及系統安全與新技術國家重點實驗室（重慶大學） 重慶　400030.重慶大學自動化學院　重慶　400030）

?

三線圈ICPT系統中繼線圈的位置優化

孫躍1，2李云濤2葉兆虹2戴欣2
（1.輸配電裝備及系統安全與新技術國家重點實驗室（重慶大學） 重慶400030
2.重慶大學自動化學院重慶400030）

三線圈感應耦合電能傳輸（ICPT）系統在給定工作頻率下，中繼線圈與原級線圈、負載線圈間的互感及負載大小是影響系統電能傳輸效率的主要因素。針對線圈間互感與線圈位置的相互約束關系，提出一種在任意給定原級線圈和負載線圈條件下的中繼線圈位置優化模型。該模型以電能傳輸效率為優化目標，綜合考慮三個線圈相互間的互感和負載等參數，通過計算機輔助設計，解決了尋找中繼線圈最優位置的問題，理論和實驗結果具有較好的一致性，且展示出中繼線圈的最優位置與負載大小密切相關。

三線圈感應耦合電能傳輸（ICPT） 中繼傳輸效率最優位置

0　引言

感應耦合電能傳輸（Inductively Coupled Power Transfer，ICPT）技術是一種利用高頻電磁場實現電能的非接觸供給技術，較傳統接觸式電能傳輸技術有無可比擬的優點，目前在國內外有著廣泛而深入地研究［1-4］，并已成功應用于家電無線供電、電動汽車無線充電、生物體實時供電等領域［5-11］。

在ICPT系統中，無線供電傳輸距離仍局限在較小尺度范圍內［12］。當負載諧振端與原級諧振端有很大的距離時，原級線圈與負載線圈的耦合互感隨著線圈間距急劇下降，導致電能傳輸功率和系統傳輸效率急劇減小。目前遠距離無線傳輸一般利用微波、激光傳能，但此傳輸電能方式效率低下。對于提高中程距離（傳輸距離大于幾何尺寸）的無線電能傳輸效率的主要措施有增大原級線圈與負載線圈的互感、使用低電阻材質的線圈材料提高線圈的品質因數、在ICPT系統中引入中繼諧振線圈。目前研究較多的中繼ICPT系統有三線圈結構［13-15］、四線圈結構［16］和多線圈結構［17］。在四線圈結構和多線圈結構ICPT系統中，系統雖能獲得較高的電能傳輸效率和傳輸距離，但系統參數的設計較復雜，易受環境的影響而偏離正常工作點，且無形中增加了系統成本，不利于實際應用。

中繼諧振網絡是無線電能傳輸系統中極為重要的“電能接力單元”，其主要功能是在保證線圈材質一定的情況下，能夠有效地提高電能的傳輸距離、傳輸功率和系統效率［18］。目前針對多線圈無線電能傳輸系統，主要是研究各耦合線圈耦合系數與傳輸效率、傳輸功率的關系，而針對中繼線圈最優位置的研究相對較少。由于中繼線圈的位置是決定傳輸能效的重要因素，本文則針對三線圈ICPT系統，在給定原、副邊（平面螺旋線圈）參數的情況下，通過尋優方法可以找到中繼線圈的最優位置。最后通過搭建實際ICPT系統裝置，對理論分析結果進行了實驗驗證。

1　系統數學模型

三線圈ICPT系統的電路等效模型如圖1所示，其中，L1為原級諧振回路電感，L2為中繼諧振回路電感，L3為負載諧振回路電感；C1、C2、C3分別為原級諧振回路、中繼諧振回路、負載諧振回路的調諧電容；R1、R2、R3分別為原級諧振回路、中繼諧振回路、負載諧振回路的內阻；R為負載電阻；M12為原級諧振回路電感和中繼諧振回路電感之間的互感，M23為中繼諧振回路電感和負載諧振回路電感之間的互感，M13為原級諧振回路電感和負載諧振回路電感之間的互感；U為系統輸入電壓；I1、I2、I3分別為原級諧振回路、中繼諧振回路、負載諧振回路的電流，箭頭方向為電流正方向。

圖1　三線圈ICPT系統電路Fig.1　The 3-coil inductively coupled powertransfer system circuit

ICPT系統諧振線圈結構位置示意圖如圖2所示。其中，Np、Nr、Ns分別為原級線圈、中繼線圈、負載線圈的線圈匝數，r1、r2、r3和 r1'、r2'、r3'分別為原級線圈、中繼線圈、負載線圈的內徑和外徑。中繼線圈與原級線圈的圓心距離為h1，ζ表示中繼線圈偏移z軸的角度，原級線圈與負載線圈的圓心距離為h2；以原級線圈的圓心O為原點建立空間直角坐標系。原級諧振線圈與輸入電源U相串聯，負載諧振線圈與負載電阻R相串聯；為了最大化傳輸電能，減少空間耦合時不必要的電能輻射、內耗等電能耗散，各線圈均采用串聯諧振方式接入諧振電容。諧振線圈電能由輸入電源注入，經過原級諧振網絡，到負載諧振網絡產生高頻電壓和電流供給負載，中繼線圈的引入使得原級線圈和負載線圈耦合度增強，與不加中繼線圈的結構相比，負載能夠獲得更多的電能。

圖2　線圈結構位置示意圖Fig.2　Schematic diagram and locations of the three coils

由圖1可以看出，為了保證系統處于諧振狀態，設置激勵源頻率為ω，并選取相應合適的調諧電容使得三個諧振回路的諧振頻率與電壓源的頻率相等，則根據互感耦合理論，可建立式（1）所示矩陣方程。

由式（1）可解出負載電流I3的表達式為

此時系統輸出功率Pout可表示為

通過計算可得到式（4）所示的三線圈ICPT系統的電能傳輸效率表達式。

三線圈ICPT系統完全諧振狀態下，由式（4）易知，系統效率η為

由式（5）可知，對于給定的工作頻率和工作負載，線圈互感對系統效率η有著極為重要的作用。現有的ICPT系統中，描述互感的公式［13-15］很少從機理上去對線圈結構進行建模分析，已有的對線圈互感建模公式［17］又不夠精確。文獻［19］描述了空間中任意兩單匝圓形線圈在兩線圈任意半徑、任意角度、任意擺放位置情況下，互感公式計算的有效性，并通過與文獻［20，21］進行對比，在理論上驗證了該互感計算公式的有效性和精確性，本文通過對平面螺旋線圈進行建模，并通過實驗驗證該理論的有效性，以得出中繼線圈位置與系統效率的關系，對于空間中任意位置單匝圓環線圈，其互感可表示為［19］

式中，μ0為真空磁導率；φ為積分因子；RS為次級線圈半徑；且互感表達式中的變量 p1～p5和 V0可定義為

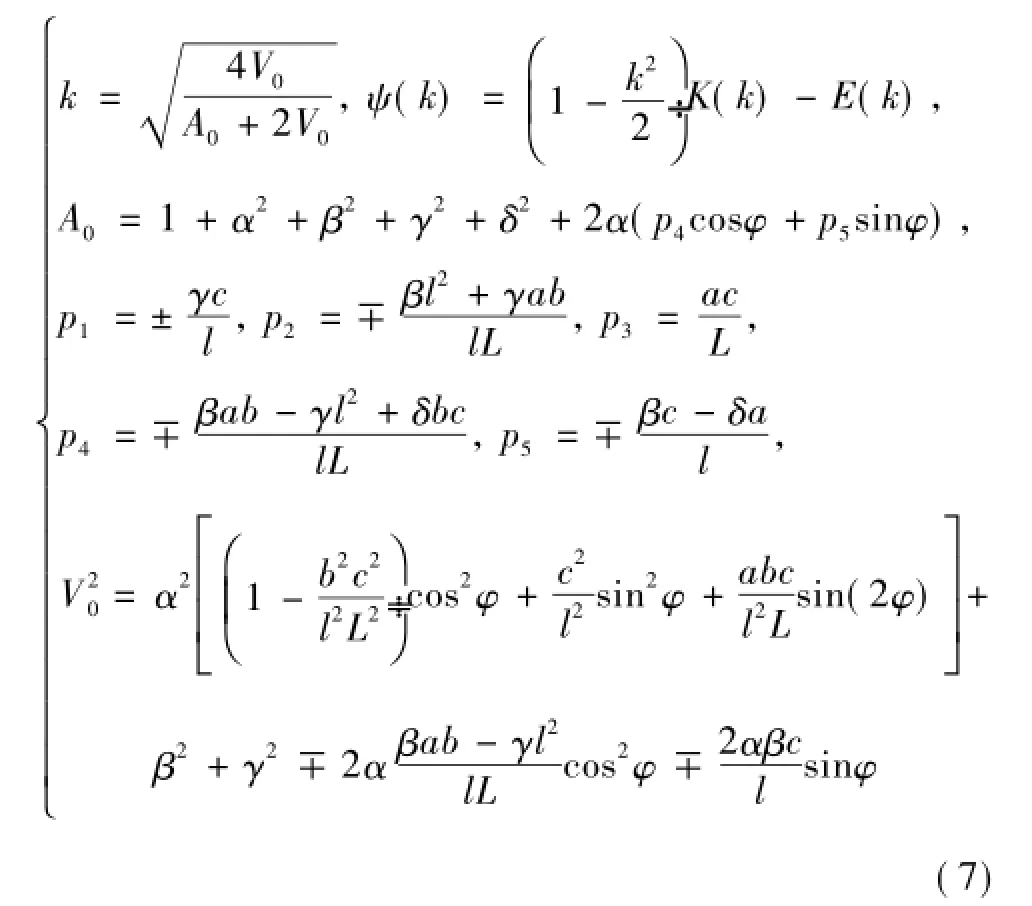
圖3　多匝螺旋線圈結構Fig.3　The schematic structure of multi-turn spiral coil

為了得到多匝線圈間的互感公式，把螺旋線圈看成匝數為Nk、半徑不等的單匝線圈，通過相互疊加可以得出空間中螺旋線圈間的互感表達式為

本文所建立的ICPT系統，原級諧振線圈、中繼諧振線圈、負載諧振線圈均為多股利茲線繞成的密集螺旋狀線圈。由于結構完全相同的線圈的耦合系數明顯高于結構不同的線圈，其內徑相差越大，耦合系數越低［22］。為了保證系統有較高的耦合系數，往往線圈參數設計成一致，即L1=L2=L3=L，Np=Nr=Ns= N，R1=R2=R3。

2　尋優方法

在線圈參數給定情況下，且線圈位置與線圈互感有著直接的關系，線圈互感對線圈效率又起著決定性作用。為了找到三線圈ICPT系統在效率最優時的中繼位置，采用球面遍歷方法。該遍歷方法為:以原級線圈的圓心為球心，中繼線圈的圓心在半徑h1的球面上做球面運動，且原級線圈平面與中繼線圈平面的法線方向始終保持平行。

基于互感球面遍歷方法，可以根據互感的區域不同，設置相應線圈擺放位置。定義σ為中繼線圈圓心連接球心O的直線在xOy平面上的投影與x軸的夾角，ζ表示中繼線圈圓心連接球心O與z軸的夾角。由于中繼線圈軸向與原級線圈、負載線圈軸向一致，中繼線圈在h1、ζ不變的情況下，與σ無關，取σ為π/2，式（10）可化簡為

上述將三維球面遍歷化簡為二維尋優問題，此時中繼線圈的位置由ζ和h1共同描述，則可建立線圈位置與互感為

實際計算機仿真過程中，ζ和h1的值可以設置成任意小步長，若ζ和h1設置成任意小時，這可以將球面中任意一點的位置遍歷完全，此時仿真時間較長，但計算機計算時間可以接受。

通過線圈間互感與位置的描述關系，聯立式（5）和式（12）可得

由式（13）可以看出系統傳輸效率η與系統工作頻率ω、工作負載R、線圈匝數N2、線圈密繞程度r2和r2'以及線圈位置ζ和h1有關。固定工作頻率ω、不同負載R時，對于一種特定的線圈匝數N2及線圈密繞程度r2、r2'，可以建立線圈最優位置ζ、h1與系統工作效率ηmax的對應關系

由上述理論分析過程將三維球面遍歷中繼線圈最優位置問題轉換為二維中繼線圈位置尋優過程。由式（12）易知中繼線圈與原級線圈、負載線圈間互感是ζ和h1共同作用的結果；通過改變中繼線圈的ζ和h1可做出互感變化關系圖，進而由式（4）和式（14）得出在定負載的情況下，系統傳輸效率與ζ和h1的變化曲線，最后通過實驗驗證在系統最大傳輸效率時，中繼線圈最優位置的合理性。

3　實驗設計與驗證

本文設計的驗證系統給定參數如下:工作頻率為85 kHz，傳輸距離 h2為30 cm，系統工作效率 η≥70%，系統輸出功率為40 W。

3.1線圈最優位置的設計過程

為了找到滿足系統工作效率η≥70%的最優位置，取N=11，線圈外徑尺寸 r2'=12.5 cm，內徑 r2= 9.75 cm；線圈繞制線采用線寬wi為2.3 mm，多匝線圈匝間的平均間隙si為0.2 mm。中繼線圈遍歷半徑h1隨中繼線圈位置ζ變化時，原級諧振線圈與中繼諧振線圈互感M12、中繼諧振線圈與負載諧振線圈互感M23如圖4、圖5所示。

圖4　互感M12與中繼線圈位置ζ的關系Fig.4　The relationship between mutual inductive M12and the position of relay coil

圖5　互感M23與中繼線圈位置ζ的關系Fig.5　The relationship between mutual inductive M23and the position of relay coil

圖4中，h1分別為5 cm和10 cm時，隨著ζ的增大，線圈的正對面積減小，但線圈垂直距離也減小，導致互感M12出現“上翹”現象；而h1為15 cm時，隨著ζ的增大，盡管線圈垂直距離、線圈正對面積減小，但由于此時遍歷半徑與線圈尺寸相近，導致互感M12出現緩慢下降；而h1分別為20 cm和25 cm時，隨著ζ的增大，由于線圈垂直距離、線圈正對面積這兩個因素相互制約著互感的變化，使得互感M12在ζ為1.22時出現“凹槽”現象。圖5中互感M23隨著ζ的增大而減小，是因為中繼線圈與負載線圈垂直距離增大、正對面積減小的緣故。

通過仿真測得在h2=30 cm情況下，線圈L1和L2的距離h1由5～25 cm每隔5 cm變化，通過改變ζ，每間隔10°得出在h1情況下中繼線圈在不同位置的關系，如圖6所示。

圖6　中繼線圈遍歷位置示意圖Fig.6　Traverse positions of relay coil

通過仿真可得出在各對應位置點處ICPT系統傳輸效率η與遍歷半徑h1、偏移角度ζ的關系如表1所示。

表1　不同位置的系統傳輸效率η（%）Tab.1　System transfer efficiency η（%）of different positions

由表1可以看出，滿足ICPT系統工作效率η≥70%位置分別為中繼線圈在h1=15 cm處，偏移角度ζ 在0°～20°之間，且ζ為0°時，系統傳輸效率較高，為81.7%；而h1=20 cm時，偏移角度ζ在0°～30°之間也滿足設計要求，ζ為10°時，系統傳輸效率最高，為84.8%；h1=25 cm時，ζ為20°，只有這個位置滿足系統設計要求。

不同位置下的最大傳輸效率與負載關系如圖7所示，當負載R=1 Ω時，遍歷半徑h1=10 cm，ζ=0°，此時系統最優傳輸效率ηmax為84.6%。當負載R= 20 Ω時，遍歷半徑h1=20 cm，ζ=0°，此時系統最優傳輸效率ηmax為84.5%。此兩種負載情況下，中繼線圈與原級線圈、負載線圈無偏移平行放置，位置最優。

圖7　不同位置條件下的最大傳輸效率與負載關系Fig.7　The relationship between maximum transfer efficiency and load in different positions

當負載R=5 Ω時，遍歷半徑h1=15 cm，ζ=0°，此時系統最優傳輸效率ηmax為87.2%。此時中繼線圈與原級線圈、負載線圈等間距平行放置，位置最優。

當負載R=10 Ω時，遍歷半徑h1=20 cm，ζ= 10°，此時系統最優傳輸效率ηmax為84.8%。當負載R=50 Ω時，遍歷半徑h1=25 cm，ζ=10°，此時系統最優傳輸效率ηmax為77.6%。中繼線圈與原級線圈、負載線圈偏移平行放置，位置最優。

中繼線圈的最優位置與系統負載有關，當負載為重負載時，中繼線圈靠近原級線圈，可使得傳輸效率提升，當負載為輕負載時，中繼線圈靠近負載線圈，可使得傳輸效率最優。

3.2實驗驗證

為驗證本文設計的三線圈ICPT系統最優位置遍歷方法的有效性，說明系統電能傳輸效率與線圈最優位置的關系，通過Matlab進行理論仿真分析，指導對三線圈ICPT系統的中繼線圈位置進行優化設計，以滿足電能高效傳輸；并且為了驗證本文理論研究的有效性，搭建了與理論參數一致的實驗平臺。

實驗裝置如圖8所示，直流電源經全橋逆變電路生成85 kHz的方波經原級串聯諧振生成具有一定功率的正弦交變電壓和電流，此電能經原級諧振線圈L1、中繼諧振線圈L2、負載諧振線圈L3供負載使用。

圖8　實驗裝置Fig.8　Experimental system

通過實驗與表1中滿足η≥70%的位置進行對比，得出的結果如圖9所示。從圖中可以看出，在ζ為10°，h1=20 cm時，傳輸效率達到最大，說明上述理論分析與實驗結果吻合。

圖9　系統傳輸效率Fig.9　System transfer efficiency

實驗測試過程中，實驗位置點的系統輸入功率和輸出功率如表2所示。在h1=15 cm及h1=25 cm處，系統傳輸效率均滿足設計要求，與設計和仿真的結果一致，說明了該尋優方法的正確性。在各仿真得出的最大傳輸效率點的實際測量的輸出功率均大于40 W，也滿足系統設計要求。

表2　實驗系統的輸入、輸出功率Tab.2　Input and output power of experimental system

三線圈ICPT系統輸入電壓和電流波形如圖10所示。可以看出系統在完全諧振狀態時，系統輸入側電壓和電流相位為零，此時系統的輸入阻抗虛部為零。

圖10　系統輸入電壓和電流Fig.10　Input voltage and current of experimental system

通過實驗結果和仿真數據對比，兩者具有一定的差異性，這是由線圈的繞制和測量存在一定的誤差造成的。但從理論與實驗分析可以看出，系統傳輸效率隨著中繼線圈偏移角度保持一致性變化。

4　結論

本文以三線圈ICPT系統傳輸效率為優化目標，通過對平面螺旋線圈進行機理建模，描述線圈結構、位置與互感的關系，對中繼線圈位置進行優化，以得到滿足最高效率為優化目標的中繼位置。最后通過仿真和實驗進行了驗證，結論如下:

1）該方法表明中繼線圈最優位置與負載有關，通過本文方法可以找到中繼線圈位置與系統傳輸效率一一對應關系；當負載為重負載時，中繼線圈靠近原級線圈，可提升傳輸效率，當負載為輕負載時，中繼線圈靠近負載線圈，可使得傳輸效率最優。

2）本文的尋優方法和系統建模不僅局限于平面螺旋線圈和S結構，對其他形式的線圈和結構同樣適用。

3）本文通過改變中繼線圈的遍歷半徑和角度的方法，可以遍歷到中繼線圈在原級線圈、負載線圈間的最優位置，為了建模方便，本文對平面螺旋線圈的模型用圓形環面的模型進行近似，從本質上會給優化過程帶來系統誤差，將在后續工作中對其進行改進。

［1］景無為，黃學良，陳琛，等.多組無線電能傳輸系統間效率影響因素分析［J］.電工技術學報，2015，30（14）:457-462.

Jing Wuwei，Huang Xueliang，Chen Chen，etal. Study on impacts among wireless power transmission multi-system［J］.Transactions of China Electrotechnical Society，2015，30（14）:457-462.

［2］田子建，林越，楊洪文，等.具有中繼諧振線圈的磁耦合諧振無線電能傳輸系統［J］.電工技術學報，2015，30（增1）:168-174.

Tian Zijian，Lin Yue，Yang Hongwen，et al.Magnetic coupling resonance wireless power transmission system with intermediate resonant coil［J］.Transactions of China Electrotechnical Society，2015，30（S1）:168-174.

［3］王智慧，呂瀟，孫躍，等.諧振式無線電能傳輸系統損耗模型［J］.電工技術學報，2014，29（9）: 17-21.

Wang Zhihui，Lü Xiao，Sun Yue，et al.Modeling of power loss in resonant wireless power transfer system［J］. Transactions of China Electrotechnical Society，2014，29（9）:17-21.

［4］宋凱，朱春波，李陽，等.基于磁耦合諧振的自主無線充電機器人系統設計［J］.電工技術學報，2014，29（9）:38-43.

Song Kai，Zhu Chunbo，Li Yang，et al.Design and implementation of an autonomous wireless charging robot systemusingmagneticallycoupledresonance［J］. Transactions of China Electrotechnical Society，2014，29（9）:38-43.

［5］孫躍，夏晨陽，戴欣，等.感應耦合電能系統互感耦合參數的分析與優化［J］.中國電機工程學報，2010，30（33）:44-50.

Sun Yue，Xia Chenyang，Dai Xin，et al.Analysis and optimization on mutual inductance for inductively coupled power transfer system［J］.Proceedings of the CSEE，2010，30（33）:44-50.

［6］Lanatà A，Scilingo E P，De Rossi D.A multimodal transducer forcardiopumonaryactivitymonitoringin emergency［J］.IEEETransactionsonInformation Technology in Biomedicine，2010，14（3）:817-825.

［7］WangCS，StielauOH，CovicGA.Design considerations for a contactless electric vehicle battery charger［J］.IEEE Transactions on Industrial Electronics，2005，52（5）:1308-1314.

［8］TangChunsen，SunYue，SuYugang， etal. Determining multiple steady-state ZCS operating points of a switch-mode contactless power transfer system［J］. IEEE Transactions on Power Electronics，2009，24（2）: 416-425.

［9］袁佳歆，薛鋼，趙震，等.三相逆變器無死區最優矢量控制研究［J］.電力系統保護與控制，2014，42 （24）:18-24.

Yuan Jiaxin，XueGang，ZhaoZhen，etal.New optimal dead-time elimination for three-phase voltage sourceinverters［J］.PowerSystemProtectionand Control，2014，42（24）:18-24.

［10］ 譚興國，王輝，張黎，等.具有電壓補償的四開關并網逆變器等效SVPWM控制方法［J］.電力系統保護與控制，2014，42（1）:1-8.

TanXingguo，WangHui，ZhangLi，etal.An equivalentSVPWMcontrolmethodwithvoltage compensation for four-switch inverters［J］.Power System Protection and Control，2014，42（1）:1-8.

［11］ 邱銀鋒，梁志珊.abc坐標系下空間矢量PWM實現研究［J］.電力系統保護與控制，2011，39（13）: 36-40.

Qiu Yinfeng，Liang Zhishan.Research on implementation of the space vector PWM in abc coordinates［J］.Power System Protection and Control，2011，39（13）:36-40.

［12］Sallan J，Villa J L，Llombar A，et al.Optimal design of ICPT systems applied to electric vehicle battery charge ［J］.IEEETransactionsonIndustrialElectronics，2009，56（6）:3060-3068.

［13］ 翟淵，孫躍，戴欣，等.磁共振模式無線電能傳輸系統建模與分析［J］.中國電機工程學報，2012，32 （12）:155-160.

Zhai Yuan，Sun Yue，Dai Xin，et al.Modeling and analysis of magnetic resonance wireless power transmission systems［J］.Proceedings of the CSEE，2012，32（12）: 155-160.

［14］ 傅文珍，張波，丘東元，等.自諧振線圈耦合式電能無線傳輸的最大效率分析與設計［J］.中國電機工程學報，2009，29（18）:21-26.

FuWenzhen，ZhangBo，QiuDongyuan，etal. Maximum efficiency analysis and design of self-resonance coupling coils for wireless power transmission system［J］. Proceedings of the CSEE，2009，29（18）:21-26.

［15］Ramrakyani A K，Mirabbasi S，Mu C.Design and optimization of resonance-based effiecient wireless power deliverysystemsforbiomedicalimplants［J］.IEEE Transactions on Biomedical Circuits and Systems，2011，5（1）:48-63.

［16］ Kiani M，JowUM，GhovanlooM.Designand optimization of a 3-coil inductive link for efficient wireless power transmission［J］.IEEE Transactions on Biomedical Circuits and Systems，2011，5（6）:579-591.

［17］Chi K L，Zhong W X，Hui S Y R.Effects of magnetic coupling of nonadjacent resonators on wireless power domino-resonatorsystems［J］.IEEETransactionson Power Electronics，2012，27（4）:1905-1916.

［18］ 羅斌，生茂堂，吳仕闖，等.磁諧振耦合式單中繼線圈無線功率接力傳輸系統的建模與分析［J］.中國電機工程學報，2013，33（21）:170-177.

LuoBin，ShengMaotang，WuShichuang，etal. Modeling and analysis of magnetic resonace coupling wirelessrelaypowertransfersystemwithsingle intermediatecoilresonator［J］.Proceedingsofthe CSEE，2013，33（21）:170-177.

［19］Babic S，Sirois F，Akyel C，et al.Mutual inductance calculationbetweencircularfilamentsarbitrarily positioned in space:alternative to grover's formula［J］. IEEETransactionsonMagnetics，2010，46（9）: 3591-3600.

［20］Fernandez C，Prieto R，Garcia O，et al.Coreless magnetic transformer design procedure［C］//IEEE 36th PowerElectronicsSpecialistsConference，Recife，2005:1548-1554.

［21］Grover F W.The calculation of the mutual inductance of circular filaments in any desired positions［J］.IEEE Proceedings of the IRE，1944，32（10）:620-629.

［22］Zierhofer C M，Hochmair E S.Geometric approach for coupling enhancement of magnetically coupled coils［J］. IEEE Transactions on Biomedical Engineering，1996，43（7）:708-714.

孫躍男，1960年生，教授，博士生導師，研究方向為無線電能傳輸、電力電子、控制理論應用與自動化系統集成。

E-mail:syue06@cqu.edu.cn（通信作者）

李云濤男，1990年生，碩士研究生，研究方向為智能電力電子和無線電能傳輸技術。

E-mail:676881999@qq.com

Optimization for Relay Coil Location of 3-Coil Inductively Coupled Power Transfer System

Sun Yue1，2Li Yuntao2Ye Zhaohong2Dai Xin2
（1.State Key Laboratory of Power Transmission Equipment&System Security and New Technology Chongqing UniversityChongqing400030China
2.College of AutomationChongqing UniversityChongqing400030China）

As for the 3-coil inductively coupled power transfer system（ICPT），in the given frequency，the mutual inductance between relay and primary coils，the mutual inductance between relay and load coils，and the load are the main factors that affect the efficiency of power transmission.By considering themutual inductances between the coils and the constraint relationship of the coil location，an optimization model of the relay coil location with the arbitrarily given primary and load coils is proposed.With the power transfer efficiency as the optimization objective，this model considers the mutual inductances of the three coils，the load，and other parameters.The relay coil'soptimal location problem is then solved with compter aided design.Experimental results are well consitent with theoretical analysis.The optimal location of the relay coil is closely related to the load.

3-coil，inductively coupled power transfer（ICPT），relay，transfer efficiency，optimal location

TM131.4+1

國家自然科學基金重點項目（51277192）、國家自然科學基金（51377183）和國家高技術研究發展（863）計劃（2015AA010402）資助。

2015-05-20改稿日期 2015-08-27