面向電磁裝置磁-熱耦合分析的異型網格映射方法

張宇嬌　秦威南　劉東圓　吳剛梁（.三峽大學電氣與新能源學院　宜昌　440022.清華大學電力系統國家重點實驗室　北京　00084.國網浙江省電力公司金華供電公司　金華　200）

?

面向電磁裝置磁-熱耦合分析的異型網格映射方法

張宇嬌1，2秦威南3劉東圓1吳剛梁1
（1.三峽大學電氣與新能源學院宜昌443002
2.清華大學電力系統國家重點實驗室北京100084
3.國網浙江省電力公司金華供電公司金華321001）

采用弱耦合有限元法求解電磁裝置中的電磁場、流場和溫度場的耦合問題時，電磁場計算得到的能量損耗要通過網格傳遞到溫度場作為載荷，結合空氣或液體的散熱進行熱分析。由于電磁場和熱-流場在求解時對網格離散要求相差很大，因此若要兼顧各種場的要求需剖分成統一的有限元模型，勢必會造成網格單元數很大、提高計算代價。而如果采用不同的網格模型，則無法實現網格間的數據直接映射。提出一種異型網格映射法，通過高斯積分及坐標變化來實現不同場之間不同網格的數據映射。此外，還提出了該方法的精度控制策略及誤差修正系數，以保證計算結果的準確性。將異型網格映射法應用于文獻中空氣絕緣三相母線槽熱分析中，將計算結果與常規同型網格直接映射方法及實驗結果進行對比，進一步驗證了該方法的有效性。

電磁裝置磁-熱耦合分析弱耦合異型網格映射法

0　引言

準確的熱分析是電磁裝置優化設計、防止過熱的前提。電磁裝置工作時，電流在導體中產生能量損耗，這些損耗轉變為熱能，使導體溫度升高，溫度過高會影響裝置的絕緣性能和機械強度，降低使用壽命［1-4］。為了降低電磁裝置的溫度，一般采用風冷和水冷進行冷卻［5，6］。因此，在電磁裝置內部會產生復雜的耦合物理現象，要準確計算其相關的電磁場、流場和溫度場是一個比較復雜的耦合場計算問題。

耦合分析通常有兩種方法:強耦合分析和弱耦合分析。第一種方法通過單元矩陣或載荷向量把耦合作用構造到控制方程中，然后對控制方程直接求解；第二種方法是在每一步內分別把相關的控制方程依次求解，通過把第一個物理場的結果作為外載荷施加于第二個物理場來實現兩個場的耦合。強耦合分析的主要缺點是在構造控制方程過程中常常不得不對問題進行簡化，計算準確度很難保證。弱耦合分析的優點是可以重新利用現有的通用軟件，并且可以分別對每個軟件單獨制定合適的求解方法［7］。目前，絕大多數研究實施的是“弱耦合分析”解決方案，即通過將電磁場分析計算的能量損耗結果作為載荷施加到流體-溫度場分析中的方式來實現耦合［8-25］。在以往的弱耦合求解方法中，根據能量損耗的加載方式不同分為兩種:一種是使用不同的專業軟件進行不同物理場的求解，例如在Ansoft、MagNet、Flux等軟件中進行電磁場計算，而在 Fluent、ThermNet軟件中進行流體-溫度場計算［10-16］；另一種是使用同一款軟件進行不同物理場的求解，例如在Ansys的Mechanical APDL模塊中建立統一的有限元模型，將電磁場計算出來的能量損耗由網格直接映射到流體-溫度場進行計算［17-22］。第一種方法的缺點是兩種軟件無法形成統一的有限元模型，則無法通過網格直接進行數據的傳遞，因此通常采取體載荷的加載方式，導致熱源加載不夠準確。第二種方法的缺點是統一的有限元模型，必須同時兼顧電磁場和流場對網格離散的要求，導致網格數量大大增加，提高了計算代價。

針對上述方法的種種缺陷，Ansys公司在2011年發布的13.0版本Workbench中推出了Ansoft軟件和Fluent軟件的接口功能，可實現不同剖分單元模型間的數據傳遞［23-25］。但它所采用的方法是通過讀取Fluent軟件中計算模型網格重心，并將此重心點對應到Ansoft軟件的計算模型中讀取相應的損耗值，以此作為整個網格的能量損耗［26］。由此可見該方法過于簡單且造成了較大的數據傳遞誤差。基于上述問題，本文提出一種通過高斯-勒讓德積分和坐標變換的異型網格映射方法實現異型網格間的數據傳遞，并提出精度控制策略及引入修正系數對傳遞結果進行修正以提高計算精度。將該方法應用于文獻［27］中的三相母線槽模型，進行電磁場、流場及溫度場的有限元計算，其中電磁場和熱-流耦合場分別使用不同的有限元網格離散策略，單元功率損耗的傳遞通過異型網格映射方法實現，計算結果與文獻中實驗結果進行比較，表明了本方法的準確性和適用性。

1　異型網格映射法的基本原理

在流體力學計算中，對流擴散方程的求解是一個迭代過程，其有限元求解需要與場分布匹配較好的網格，否則會出現劇烈的數值偽振蕩現象，導致迭代不收斂［28］。因此，在流場的有限元計算中對網格質量的要求非常高，3-D模型一般要使用規則的六面體或者三棱柱單元剖分，3-D熱-流耦合場網格如圖1a所示。這種模型在流固交界處由于速度變化較大，需要嚴格控制網格精度。圖1b所示的四面體非規則型網格難以保證計算過程的收斂性，但在電磁場計算中，具有對復雜場域適應性強、網格疏密靈活等優點，所以四面體單元的非規則型網格則是電磁場計算的首選網格類型。

圖1　不同物理場的不同3-D網格離散形式Fig.1　Different 3-D meshes in different fields

為了實現在電磁計算中采用四面體非規則型網格，在熱和流體冷卻問題計算中采用結構型網格，本文提出一種異型網格間的場量映射法，將電磁場能量損耗計算結果通過該映射的方法傳遞給溫度場計算網格作為載荷。不同網格間通過高斯積分點進行關聯，即溫度場一個單元上的熱載荷總量通過高斯積分得到。而積分點上的電流密度值取自電磁場中的相同幾何點，該點的電流密度值通過電磁場單元的形狀函數插值計算得到。

為了描述方便，以二維模型為例進行闡述，對于三維模型可類似處理。在圖2所示的異型網格數據映射示意圖中，假設圖2a為熱流耦合場計算網格，圖2b為電磁場計算網格。要想得到圖2a單元①的熱載荷，可以采用高斯積分進行計算，假設每個單元上的積分點個數取為n（圖2中給出了4個點ABCD），則每個積分點的電流密度值（如圖2a中的自然坐標下A點）要到電磁場計算模型中去查找（如圖2b中的笛卡爾坐標下A點），因為電磁能量損耗就是溫度場的熱載荷量，所以單元①的熱載荷為

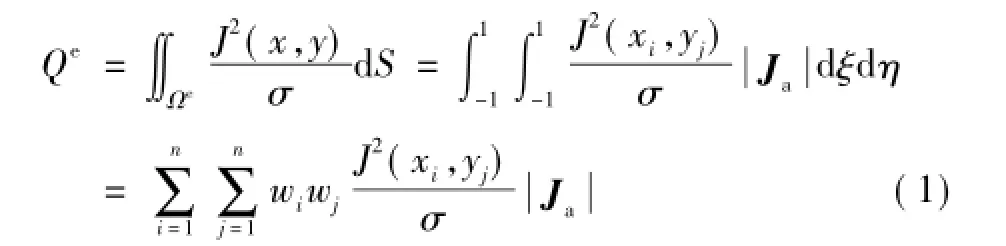
式中，Ωe為單元的積分區域；σ為電導率；S為積分面積；ξ和η為高斯積分點的自然坐標；wi和wj為各高斯積分點的權系數［29］；Ja為雅克比矩陣［30］；J（xi，yj）為各高斯點在電磁場計算模型中的電流密度。

圖2　異型網格數據映射示意圖Fig.2　Non-matching meshes mapping method

雖然該方法的原理并不復雜，但在具體實現中要注意誤差控制（包括兩種網格的大小比例控制）、積分點的選取方法、誤差判據與誤差修正方法等。而網格分布與積分點數量又與場分布有關，所以要實現具有較高精度而又不帶來過多計算量，需要在幾個環節進行分析考慮。下面將具體介紹異型網格映射方法實現時的處理策略。

2　異型網格映射方法實現與精度控制策略

針對不同場計算要求的網格特性差異，分析網格剖分策略與不同網格間單元大小的匹配關系，以及控制或減小異型網格映射法的變量傳遞誤差的方法。

2.1異型網格剖分策略

下面以半封閉槽內載流導體通風冷卻的溫升計算為例分析兩種網格的剖分問題。耦合場溫升分析模型如圖3所示，其為二維平行平面場，高為h的銅導體上加載有效值為1 000 A的工頻電流，進風口風速為0.5 m/s，材料屬性按常規設置。

圖3　耦合場溫升分析模型Fig.3　Model of thermal analysis in coupled fields

在電磁場計算中，考慮趨膚效應導致導體中渦流分布的不均勻性，需要對導體部分的邊緣區域進行加密剖分，導體內可以采用四邊形或三角形單元，導體外的空氣應該改用三角形單元，異型網格剖分策略如圖4所示。

圖4　異型網格剖分策略Fig.4　Discretization strategy in non-matching meshes mapping method

在電磁場計算中，關鍵問題是導體內的剖分控制，對于該簡單的矩形區域應該采用四邊形，為了適用于更復雜區域這里采用了三角形單元。無論是什么形狀的單元，都要使得網格單元大小分布與電流密度分布的變化率匹配，具體策略是使得每個單元中最大與最小電流密度的差值基本一致。該策略的基礎是使得相鄰單元中電流密度變化較小，滿足相鄰單元中電流接近連續的特性。

該剖分策略的實現是先估算導體內的電流分布，然后根據計算結果剖分網格。如果利用軟件直接對矩形區域進行剖分，則不能實現該策略。為了能更好地實現該策略，可以采取人為地將矩形區域劃分成許多子區域的方法，而子區域的劃分按照電流密度的估算分布來設置，即將矩形區域從外向內分成若干帶狀矩形子區域，每個帶的寬度與電流密度分布匹配。然后再通過軟件對每個子區域剖分就可以實現理想分布的網格了。

在熱-流耦合場計算中，流固交界面是兩種不同介質間的邊界，當交界面發生運動變化，在交界面處附近區域的網格質量直接影響計算精度和收斂性［31］。同樣人為地將矩形導體與空氣交界區域劃分成若干子區域，而子區域的劃分根據空氣流動速度的估算來設置，在區域中采用四邊形網格映射剖分，網格密度與空氣流速匹配。此外，導體部分為異型網格映射區域，由于不涉及空氣流動影響可均勻劃分網格，如圖4b所示。

2.2積分點個數與單元大小比例選擇策略

在對式（1）進行數值計算時，顯然，高斯積分點選取越多計算結果越準確，但是勢必造成計算量增大。因此，在工程計算精度允許范圍內，應選取盡量少的高斯積分點以減少計算量和提高計算速度。

實際上，基于式（1）的損耗映射計算精度主要受到四個因素的影響:電流密度分布的變化率、積分點數量、一個熱-流場單元包含的電磁場單元數量、電磁計算的單元形狀函數階數，四個因素相互關聯。熱-流場中某一單元對應于電磁場中若干單元如圖5所示，這里假設熱-流場是在單元上施加均勻熱載荷而計算的，否則，還應考慮熱-流場單元的最大尺寸控制問題。下面主要分析在一個熱-流場單元中，應該如何選擇積分點個數和電磁單元個數。

圖5　熱-流場中某一單元對應于電磁場中若干單元Fig.5　Several elements in electromagnetic field matched with one element in thermal and fluid field

顯然，如果電流密度在導體中分布比較均勻，則熱-流場單元中包含的電磁單元個數和積分點個數就可以較少。反之，在電流密度變化較大的導體拐角處和受趨膚及臨近效應影響較大的區域，要求電磁單元個數和積分點個數較多。換言之，在電磁場計算網格一定的情況下，確定熱-流場單元在具體場域位置中的大小，就要依據下面討論的一個熱-流場單元最多可包含的電磁單元數量的方法來進行剖分控制。

容易理解，積分點個數越多，容許一個熱-流場單元中包含的電磁場單元數就越多，若積分點數為n2，（即二維問題中每個方向上的積分點數為n），則所包含的電磁場單元的個數不能大于n2，否則會有電磁場單元在積分中沒有用到。反之亦然，若包含的電磁場單元數為m，則積分點總數不能小于m。這就是一個熱-流場單元中積分點數與電磁場單元數量的控制策略。

如果電磁場計算采用線性單元，電流密度在一個單元內為一個常數，則沒必要選取過多的積分點，因為一個電磁場單元內落入一個積分點就可以保證較高的映射準確度。在線性單元下，按照上一段給出的策略聯合控制積分點數和一個熱-流場單元中包含的電磁單元數即可。具體講，按照積分點數不小于單元數的策略進行控制；考慮到電磁單元大小的不均勻性，建議采用的積分點個數不小于電磁場單元數m的1.5倍。

如果電磁單元是二階單元，則電流密度在單元中非常數，為了體現一個單元的總電流值，最少應該有兩個積分點落在一個單元內。因此，建議采用的積分點個數不小于電磁場單元數m的3倍。

因為在上一節中已經按照電流密度分布的變化率控制了電磁場單元的分布，使得每個單元內的實際電流密度（不是指數值計算的電流密度）比較均勻，且相鄰單元間的電流密度也比較均勻，即跳變不大。因此，在這種電磁場網格下，利用上面介紹的一個熱-流場單元中的積分點和包含電磁單元最大數量的策略進行損耗映射，則可以保證較高的精度，且計算量較小。

2.3總體誤差修正方法

無論采用多少個積分點，或采用上述控制誤差的方法，損耗映射誤差必然存在，即溫度場得到的總載荷與電磁場的損耗結果會存在差異。可以利用這個總量差異來進行各單元的載荷調整，以減小誤差。具體方法是，將映射至熱-流場模型中各單元的能量損耗求和與原電磁場模型求解所得總損耗相比，得到修正系數λ，如式（2）所示，然后將各單元映射得到的熱載荷值除以該修正系數即可。

2.4計算結果

根據以上描述方法及策略，采用異型網格映射后溫度場計算結果如圖6a所示。提取異型網格和同型網格兩種計算方法得到的模型觀測線溫度分布對比如圖6所示。由圖6可知，采用異型網格映射方法得到的計算結果與常規匹配網格直接映射方法具有很好的一致性，而計算時間減少13%，若將來應用在三維模型中計算時間可減少更多。

圖6　溫度計算結果對比Fig.6　Comparison of temperature calculation results

3　基于異型網格映射的母線槽耦合場計算

為了驗證異型網格映射方法的準確性，針對文獻［27］所提供的空氣絕緣型母線槽耦合場的熱分析［32-35］先通過電磁場計算求出能量損耗，再通過異型網格映射法傳遞熱載荷進行溫度求解，實現異型網格間的數據映射。

3.1模型與有限元網格

根據文獻［27］中提供的三相四線制空氣絕緣型母線槽模型尺寸建立2D計算模型，該模型無通風結構，由鋼質外殼封裝，矩形母線導體從左到右排列，依次為母線導體的A、B、C和N相。模型中各部分材料屬性與文獻［27］中設置相同。電流載荷、熱對流、熱輻射以及熱傳導邊界條件均按文獻中所提供數值進行設置［27］。

不同物理場的不同有限元模型如圖7所示，電磁場計算中使用三角形網格，導體部分加密剖分共2 400個單元，總體網格數為5 830。流場計算中使用四邊形網格，流固交界處加密剖分，導體內部粗剖共240個單元，總體網格數為12 694。

圖7　不同物理場的不同有限元模型Fig.7　Different finite-element models in different fields

3.2異型網格映射方法的計算結果及分析

母線導體和鋼制外殼電流電磁場計算結果如圖8所示。從圖8中可以看出，電流密度分布具有明顯的趨膚效應和鄰近效應。

圖8　電磁場計算結果Fig.8　Calculation results of electromagnetic field

對溫度場計算每個四邊形單元采用四個高斯積分點。根據式（2），得到修正系數為0.95所得到的異型網格映射方法的計算結果如圖9所示。

圖9　異型網格映射方法的計算結果Fig.9　Calculation results by different meshes mapping method

表1給出了文獻［27］中所提供的實驗數據和基于異型網格映射法和兩種場利用相同網格（單元數19 550）的同型網格法的仿真計算溫度值與實驗結果對比。由表1中誤差值可知，兩種網格計算結果基本一致，與實驗值相差都小于5%。而異型網格的電磁計算單元數僅為同型的1/3。若計算三維問題，網格數相差會更大。因此，異型網格法具有較高的計算效率。

表1　仿真計算溫度值與實驗結果對比Tab.1　Comparison of calculation and experiment temperature

4　結論

1）采用異型網格映射方法進行耦合場計算根據各個場對于網格的要求，分別進行有限元模型的網格離散，無需同時兼顧各場對網格形狀及剖分的要求，因此相對建立統一有限元模型的同型網格映射方法的耦合場計算，該方法減小了網格數量，降低了計算量，提高了計算速度。

2）異型網格映射方法的計算精度主要受到四個因素的影響:電流密度分布變化率、積分點數量、一個熱-流場單元包含的電磁場單元數量、電磁計算的單元形狀函數階數。四個因素相互關聯，需根據本文所提控制策略進一步提高計算精度。

3）本文還提出映射完成后需采用誤差修正系數對該方法進行數據修正，以提高計算精度。

4）通過應用于文獻中計算實例，將異型網格映射方法結果與常規同型網格方法以及文獻中實驗結果對比，驗證了本方法的有效性和準確性，并可將該方法應用于三維耦合場計算。

［1］陳益廣，鄭軍，魏娟，等.舵機用永磁同步電機的設計與溫度場分析［J］.電工技術學報，2015，30 （14）:94-99.

Chen Yiguang，Zheng Jun，Wei Juan，et al.Design of PMSM for actuator and its temperature field analysis［J］. Transactions of China Electrotechnical Society，2015，30（14）:94-99.

［2］陳民鈾，高兵，楊帆，等.基于電-熱-機械應力多物理場的IGBT焊料層健康狀態研究［J］.電工技術學報，2015，30（20）:252-260.

Chen Minyou，Gao Bing，Yang Fan，et al.Healthy evaluation on IGBT solder based on electro-thermalmechanical analysis［J］.Transactions of China Electrotechnical Society，2015，30（20）:252-260.

［3］黃文美，薛胤龍，王莉，等.考慮動態損耗的超磁致伸縮換能器的多場耦合模型［J］.電工技術學報，2016，31（7）:173-178.

Huang Wenmei，Xue Yinlong，Wang Li，et al.Multifield coupling model considering dynamic losses for giant magnetostrictive transducers［J］.Transactions of China Electrotechnical Society，2016，31（7）:173-178.

［4］杜海，曲延濱，張鵬.新型旋轉電磁熱機流體流動與傳熱的耦合計算與實驗［J］.電工技術學報，2015，30（12）:291-297.

Du Hai，Qu Yanbin，Zhang Peng.Coupling calculation and experiment of fluid flow and heat transfer of a new rotatinginductionheater［J］.TransactionsofChina Electrotechnical Society，2015，30（12）:291-297.

［5］段濤，楊斌，李賢慶，等.±500 kV換流站閥水冷系統隱患分析治理［J］.電力系統保護與控制，2014，42（18）:132-138.

Duan Tao，Yang Bin，Li Xianqing，et al.Analysis of potential dangers in±500 kV converter station valve water cooling system［J］.Power System Protection and Control，2014，42（18）:132-138.

［6］周封，熊斌，李偉力，等.大型電機定子三維流體場計算及其對溫度場分布的影響［J］.中國電機工程學報，2005，25（24）:128-132.

Zhou Feng，Xiong Bin，Li Weili，et al，Numerical calculation of 3D stator fluid for large electrical machine as well as influences on thermal field distribution［J］. Proceedings of the CSEE，2005，25（24）:128-132.

［7］王彬，楊慶山.弱耦合算法的實現及其應用［J］.工程力學，2008，25（12）:48-53.

Wang Bin，Yang Qingshan.Realization and application of loosely coupled algorithm［J］.Engineering Mechanics，2008，25（12）:48-53.

［8］Alberti L，Bianchi N.A coupled thermal-electromagnetic analysis for a rapid and accurate prediction of IM performance［J］.IEEETransactionsonIndustrial Electronics，2008，55（10）:3575-3582.

［9］程志光，高橋則雄，博扎德·弗甘尼.電氣工程電磁熱場模擬與應用［M］.北京:科學出版社，2009.

［10］ 王海軍，王寧，楊仕友，等.基于 ThermNet和MagNet的水輪發電機端部電磁、溫度場仿真研究［J］.電工技術學報，2013，28（2）:116-121.

WangHaijun，WangNing，YangShiyou，etal. Numerical calculations of the coupled eddy currenttemperature fields in the end regions of large hydrogeneratorusingmagnetandthermnetsoftware［J］. Transactions of China Electrotechnical Society，2013，28（2）:116-121.

［11］ 劉永志，李巖，井永騰.基于Fluent軟件的電力變壓器溫度場計算與分析［J］.高壓電器，2012，48 （10）:6-11.

Liu Yongzhi，Li Yan，Jing Yongteng.Calculation and analysis of temperature field of power transfer based software fluent［J］.High Voltage Apparatus，2012，48 （10）:6-11.

［12］宋帆.800 kV GIS隔離開關磁場-溫度場計算與分析［J］.高電壓技術，2008，34（7）:1383-1388.

Song Fan.Calculation and analysis on magneto-thermal fields of 800 kV GIS disconnector［J］.High Voltage Engineering，2008，34（7）:1383-1388.

［13］胡田，唐任遠，李巖，等.永磁風力發電機三維溫度場計算及分析［J］.電工技術學報，2013，28（3）: 122-126.

Hu Tian，Tang Renyuan，Li Yan，et al.Thermal analysis andcalculationofpermanentmagnetwind generators［J］.Transactions of China Electrotechnical Society，2013，28（3）:122-126.

［14］武安波，王建華，耿英三.密集型母線槽磁場-溫度場綜合有限元分析［J］.高壓電器，2003，39（4）: 7-10.

WuAnbo，WangJianhua，GengYingsan.Finite element analysis of coupled magneto-thermal fields for compactbusbartrunkingsystem［J］.HighVoltage Apparatus，2003，39（4）:7-10.

［15］孫國霞，舒乃秋，吳曉文，等.基于多物理場耦合的氣體絕緣母線觸頭接觸溫升有限元計算［J］.電工技術學報，2013，28（2）:408-413.

Sun Guoxia，Shu Naiqiu，Wu Xiaowen，et al.Finite element analysis of contact temperature rise in gas insulated busbars based on coupled multi-physics［J］. Transations of China Electrotechnical Society，2013，28 （2）:408-413.

［16］付朝陽，劉景林，趙小鵬.雙余度永磁無刷直流電機磁-熱耦合分析［J］.西北工業大學學報，2010，28（6）:921-926.

Fu Zhaoyang，Liu Jinglin，ZhaoXiaopeng.Magneticthermal coupling analysis of dual-redundancy BLDCM ［J］.Journal of Northwestern Polytechnical University，2010，28（6）:921-926.

［17］Zhang Yujiao，RuanJiangjun，HuangTao，etal. Calculation of temperature rise in air-cooled induction motorsthrough3-Dcoupledelectromagneticfluiddynamical and thermal finite-element analysis［J］.IEEE Transactions on Magnetics，2012，48（2）:1047-1050.

［18］范鎮南，張德威，陳顯坡，等.用電磁場和流場模型計算GIS母線損耗發熱［J］.高電壓技術，2008， 34（12）:3016-3021.

Fan Zhennan，Zhang Dewei，Chen Xianpo，et al. Calculation of loss and heat of GIS bus bar using electromagnetic field and fluid field［J］.High Voltage Engineering，2008，34（12）:3016-3021.

［19］ 關曉存，李治源，趙然，等.線圈炮電樞電磁熱耦合仿真分析［J］.強激光與粒子束，2011，23（8）: 2267-2272.

Guan Xiaocun，Li Zhiyuan，Zhao Ran，et al.Simulation analysis of electromagnetic-thermal coupling for armature in inductive coilgun［J］.High Power Laser and Particle Beams，2011，23（8）:2267-2272.

［20］ 李巖，額爾和木巴亞爾，張霄霆，等.變壓器磁熱耦合計算與局部過熱屏蔽措施［J］.沈陽工業大學學報，2012，34（4）:366-371.

LiYan，Eerhemubayaer，ZhangXiaoting，etal. Magnetic-thermalcouplingcalculationandshielding measure of local overheating for ttransformer［J］.Journal of Shenyang University of Technology，2012，34（4）: 366-371.

［21］ 額爾和木巴亞爾，李巖，孫昕.基于Ansoft的變壓器磁-熱耦合分析［J］.變壓器，2011，48（3）: 29-33. Eerhemubayaer，LiYan，SunXin.Magnet-thermal couple analysis of transformer based on ansoft［J］. Transformer，2011，48（3）:29-33.

［22］ 夏海霞，姚纓英，熊素銘，等.1 000 MW汽輪發電機端部磁-熱耦合分析［J］.中國電機工程學報，2008，28（14）:118-122.

Xia Haixia，YaoYingying，XiongSuming，etal. Magnetic-thermal coupling analysis of end region of 1 000 MWturbine-generator［J］.Proceedingsofthe CSEE，2008，28（14）:118-122.

［23］ 張琪，王偉旭，黃蘇融，等.高密度車用永磁電機流固耦合傳熱仿真分析［J］.電機與控制應用，2012，39（8）:1-5.

Zhang Qi，Wang Weixu，Huang Surong，et al.Heat transfer simulation of high density permanent magnet motor for vehicles based on fluid-solid coupling method ［J］.Electric Machines&Control Application，2012，39（8）:1-5.

［24］ 陳小軍.高速永磁無刷直流電機磁熱耦合分析與效率優化研究［D］.廣州:廣東工業大學，2013.

［25］ 李青青，黃勤，楊立，等.無刷力矩電動機電磁場-溫度場耦合仿真與分析［J］.微特電機，2013，41 （8）:30-39.

Li Qingqing，Huang Qin，Yang Li，et al.Couplinganalysis and simulation of electromagnetic field and temperature field for brushless torque motor［J］.Small andSpecialElectricalMachines，2013，41（8）: 30-39.

［26］Ansys Workbench 14.0 Help.

［27］WuAnbo，ChenDegui，WangJianhua，etal，Evaluation of thermal performance for air-insulated busbar trunkingsystembycoupledmagneto-fluid-thermal fields［C］ //Proceedings of International Conference on PowerSystemTechnology， Kunming， 2002，4: 2159-2163.

［28］甘艷，阮江軍，張宇.應用混合有限元法有限體積法處理運動電磁問題［J］.電工技術學報，2006，21 （11）:2-7.

Gan Yan，Ruan Jiangjun，Zhang Yu.A hybrid finite element methodandfinitevolumemethodforthe simulation of motion problems［J］.Transactions of China Electrotechnical Society，2006，21（11）:2-7.

［29］倪光正，楊仕友，錢秀英，等.工程電磁場數值計算［M］.北京:機械工業出版社，2004.

［30］王勖成，邵敏.有限單元法基本原理和數值方法［M］.北京:清華大學出版社，1997.

［31］周岱，馬駿，李磊.流場和流固耦合問題網格剖分與更新的新方法［J］.工程力學，2009，26（11）: 10-16.

Zhou Dai，Ma Jun，Li Lei.A novel technique for mesh generation and update in the analysis of flow field and fluid-structure interaction［J］.Engineering Mechanics，2009，26（11）:10-16.

［32］ 趙鎮南.傳熱學［M］.北京:高等教育出版社，2008.

［33］Ho S L，Li Y，Lin X，et al.Calculations of eddy current，fluid，and thermal fields in an air insulated bus duct system［J］.IEEE Transactions on Magnetics，2007，43（4）:1433-1436.

［34］Ho S L，Li Y，Lin X，et al.A 3-D study of eddy current field and temperature rises in a compact bus duct system［J］.IEEE Transactions on Magnetics，2006，42 （4）:987-990.

［35］ 武安波，張國剛.基于磁場-流場-溫度場耦合計算的母線槽熱性能分析［J］.電工電能新技術，2002，21 （3）:62-66.

Wu Anbo，Zhang Guogang.Analysis of thermal capacity for busbar trunking system by coupled magneto-fluidthermal field calculation［J］.Advanced Technology of ElectricalEngineeringandEnergy，2002，21（3）: 62-66.

張宇嬌女，1979年生，博士，副教授，研究方向為電磁場數值計算、電磁裝置多物理場耦合數值計算。

E-mail:jiao_zyj@163.com（通信作者）

秦威南男，1987年生，碩士，研究方向為多物理場耦合數值仿真計算、輸電線路及變電站帶電作業技術。

E-mail:k_meetup@163.com

Non-Matching Meshes Mapping Method in Coupled Magnetic and Thermal Analysis of Electromagnetic Devices

Zhang Yujiao1，2Qin Weinan3Liu Dongyuan1Wu Gangliang1
（1.College of Electrical Engineering and New EnergyChina Three Gorges UniversityYichang443002China
2.State Key Lab.of Power SystemTsinghua UniversityBeijing100084China
3.State Grid Jinhua Power Supply CompanyJinhua321001China）

In the coupled electromagnetic fluid-dynamical and thermal simulations which are done by the weak coupling finite element method（FEM）for the electromagnetic devices，the thermal loads obtained from the energy losses by electromagnetic calculations are transferred between meshes to calculate the temperature distributions by considering the influence of air and fluid flow.Because the requirements of the meshes discretization scheme are quite different between electromagnetic and fluid-thermal fields，the same finite element model applied to analyze both requirements will lead to increase the number of meshes and the time of calculation.However，if different finite element models are used，the data cannot be directly transferred between the corresponding meshes.In this paper，a non-matching mesh mapping method is proposed.The energy losses can be transferred between the different meshes by the Gauss integral and coordinate transformation.Moreover，the strategy of precision control and error correction coefficient are proposed to ensure the calculation accuracy.This method is applied to an air insulation bus duct system in the literature.The calculation results are compared with the normal matching meshes mapping method and the experiment results to validate the proposed non-matching meshes mapping method.

Electromagnetic devices，coupled magnetic and thermal analysis，weak coupling，nonmatching meshes mapping method

TM15

國家自然科學基金（51207081、51577106），清華大學國家重點實驗室開放基金重點（SKLD14KZ05）資助。

2014-11-01改稿日期 2015-01-30