用振動力學有限元分析方法估算多類烴的液體熱導率

仇明華，劉萬強，陳冠凡，劉鳳萍，岳　明

?

研究論文

用振動力學有限元分析方法估算多類烴的液體熱導率

仇明華1,2，劉萬強1,2，陳冠凡1，劉鳳萍1，岳明1

(1湖南科技大學化學化工學院；2理論有機化學與功能分子教育部重點實驗室，湖南 湘潭 411201)

摘要：將烴分子結構模擬成彈性體，用振動力學有限元分析方法對分子 3D結構進行有限元分析，建立分子結構體系的剛度矩陣和多自由度振動方程，用 MATLAB軟件包求解得到分子結構固有頻率和剛度矩陣特征值，將分子結構固有頻率和剛度矩陣特征值作為參數，用多元回歸方法建立液態烴類熱導率QSPR模型。該模型對訓練集581個多類烴的液態熱導率的計算值與實驗值的相關系數為0.9874，平均絕對誤差小于0.00259 W·m-1·K-1，平均相對誤差小于2.39%；對測試集22個烴類化合物熱導率的預測值與實驗值的相關系數為0.9550，平均絕對誤差小于0.00263 W·m-1·K-1，平均相對誤差小于2.42%。該計算模型的計算值和實驗吻合，可用于鏈烴、烯烴、炔烴及單環烷烴、多環烷烴、萘烷、芴烷、菲烷、茚烷、蒎烷等復雜結構烷烴的液體熱導率的計算。

關鍵詞:熱導率；熱傳導；熱力學性質；分子結構參數；有限元分析

引 言

熱導率是化工、生物、冶金、機械、石油和能源等工程領域傳熱設計中需要的重要基礎數據，也是采暖、保溫、傳熱、散熱、制冷等工程中尋找合適熱交換器的重要依據，同時也是化合物最重要的物理性質之一。由于有機物種類繁多，如果通過實驗測定工作量太大，有些化合物實測起來也許非常困難。因此，尋找化合物熱導率數據更加準確和簡便的計算方法一直是化學和化工領域研究的重點課題之一。

從已有的熱導率的計算方法[1-19]來看，可分為基于分子運動理論方法和基團貢獻法等。這些方法大多都離不開對化合物其他物理性質的依賴，如Latini法、Sastri方法和Teja方法[1-3]，都是在對比溫度基礎上進行估算的。有些方法是以熱導率實驗值為前提的，如后續的基團貢獻法、拓撲指數法、神經網絡法和偽格法等[4-8]。同時為了減小熱導率計算值與實驗值的誤差，對計算方法的約束條件也越來越多，如Arikol和Gurbuz方法[10]，Dana和Dabir[11]方法等需要溫度、臨界溫度、臨界壓力、分子量和標準沸點等。

因此探索從分子結構直接計算熱導率(不依賴化合物的其他實驗數據和物理性質)是非常有意義的工作。這方面的研究始于Jamieson等[12-13]，在給出一個估算λL的通用方程后，再分析分子結構和分子大小對方程中常數的影響。張克武等[14]基于氣體不平衡理論方程推導出液體熱導率估算方程，同樣也是將分子結構的影響歸結為不同碳原子數、不同化學鍵和不同基團對方程系數的影響，并將溫度的影響通過臨界溫度和熔點劃分為不同的溫度段，使純質液體熱導率的估算誤差遠遠小于Latini方法的誤差。直接用分子結構參數來計算純質液體熱導率的研究始于文獻[15-17]。仇明華等[15]以4個基團參數、1個極化效應指數PEI和1個溫度參數，對45個鏈烷烴分子的155個熱導率數據建立了高相關性估算模型。曹晨忠等[16]采用了拓撲量子方法，以鍵鄰接矩陣特征根為參數，對45種鏈烷烴在不同溫度下的155個熱導率數據進行回歸，建立了4參數擬合方程。聶長明等[17]從鏈烷烴分子中各原子的電負性效應、支化效應及空間效應出發，構建了結構拓撲指數PXm，對液相鏈烷烴在不同溫度的155個熱導率數據點建立了4參數的定量構效關系模型。此外萬麗華等[18-19]采用EMD方法Green-Kubo理論采用動力學模擬客體分子數對烴類水合物熱導率的影響。盡管上述方法有所突破，但理論不夠具體，經驗性非常明顯，因而局限了估算方程的應用范圍。

物質熱量傳遞機理[20]認為液體分子處在其周圍相鄰分子形成的“分子籠”中，通過分子的運動（分子、原子或電子的平動、振動和轉動）來傳遞動量和能量。然而由于人們對液體分子運動仍然不能精確描述，同時分子可能以某種形式儲存能量等原因，對液體分子的運動和熱傳導仍然不能用公式準確描述。空間剛架元分析[21-22]是機構振動力學分析的有效手段之一。它將一個結構看成是由多個空間桿元和節點構成的體系。其中的空間桿元是沒有質量的彈性體，體系的整體質量分散在各節點上，這與分子結構非常契合。在分子中，化學鍵就相當于一個沒有質量的空間桿元，也可以認為是一個沒有質量的彈性體，原子或基團就相當于桿元的節點，是整個分子質量的分散點。這與物質通過內部原子、分子的振動和相互碰撞進行熱量傳導的導熱機理吻合。

利用彈性細桿非線性力學方法中的DNA力學模型理論，可以計算每個化學鍵空間桿元的6個參數，即彈性模量、剪切彈性模量、橫截面積、長度、慣性矩和極慣性矩。求出整體剛度矩陣的特征值和多自由度分子結構體系振動方程的特征根——固有頻率。可以用各階特征值的平均絕對值和各階固有頻率之和作為定量構效關系(QSPR)模型參數，應用于液態烴類熱導率的計算。

1　理論與方法

1.1 分子結構建立和優化

用空間剛架元分析分子結構時，首先確定剛架元節點的空間3D坐標，即烴類分子中CHn基團的3D坐標的確定。本文首先用Chem3D繪制分子的3D結構，再導入到Gaussian 09軟件，用RHF方法，6-31G基組，優化分子結構，同時使用freq關鍵詞計算頻率，看有無虛頻以判斷優化后構型是否為最優構型。最后得到分子中原子的空間坐標。

1.2 化學鍵空間剛架元系數的定義與計算

本文將隱氫分子圖中的化學鍵定義為化學鍵空間剛架元。這樣烴類分子隱氫圖中只涉及 C—C單鍵、CC雙鍵和CC三鍵，其鍵長L可以根據輸入的分子的3D坐標計算由MATLAB有限元分析程序得到[19-20]。分子空間剛架元的其余5個系數:彈性模量(E)、剪切彈性模量(G)、橫截面積(A)、慣性矩(Ix和 Iy)、極慣性矩 Iz的值分別見表 1，其中Ix=Iy。有關6個系數的定義和計算可參見文獻[21-23]。

1.3 分子結構剛度矩陣平均絕對特征值δm的定義與計算

在定義和計算得到化學鍵空間剛架元6個系數之后，本文建立分子結構的整體剛度矩陣[21-23]。先建立單個化學鍵的單元剛度矩陣ki，最后建立分子整體剛度矩陣K。K是一個6n×6n階方陣，這里的n是指分子隱氫圖中的原子基團數，即節點數。如果隱氫分子圖中的原子基團(節點)數目越多，其整體剛度矩陣的階數就越高，在求解特征值時，可以使用MATLAB軟件求解，其程序代碼為“eig”，即

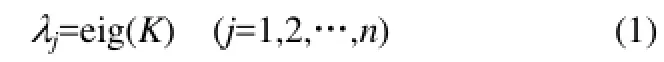
本文定義一個分子結構剛度矩陣平均絕對特征值，用“δm”表示，即

式中，|λj|為各階特征值的絕對值，以保證各階特征值在求和過程中不被正負抵消；nc為分子中的節點數，即隱氫分子圖中的原子或基團數，對于烴類分子而言，就是分子中的碳原子數。

表1　C—C單鍵、CC雙鍵和CC三鍵空間剛架元的6個參數值Table 1 Values of parameters for C—C, CC and CC bond

表1　C—C單鍵、CC雙鍵和CC三鍵空間剛架元的6個參數值Table 1 Values of parameters for C—C, CC and CC bond

Elastic Shear elastic Type of Moment of Cross-sectional Moment of Polar moment of modulus (E) Bond modulus (G) area (A) inertia (Ix) inertia (Iy) inertia (Iz) C—C 0.8322 0.2774 3.1412 0.7853 0.7853 1.5706 C C 1.4688 0.4896 2.3078 0.4239 0.4239 0.8478 C C 2.0108 0.6703 1.9023 0.2895 0.2895 0.5790

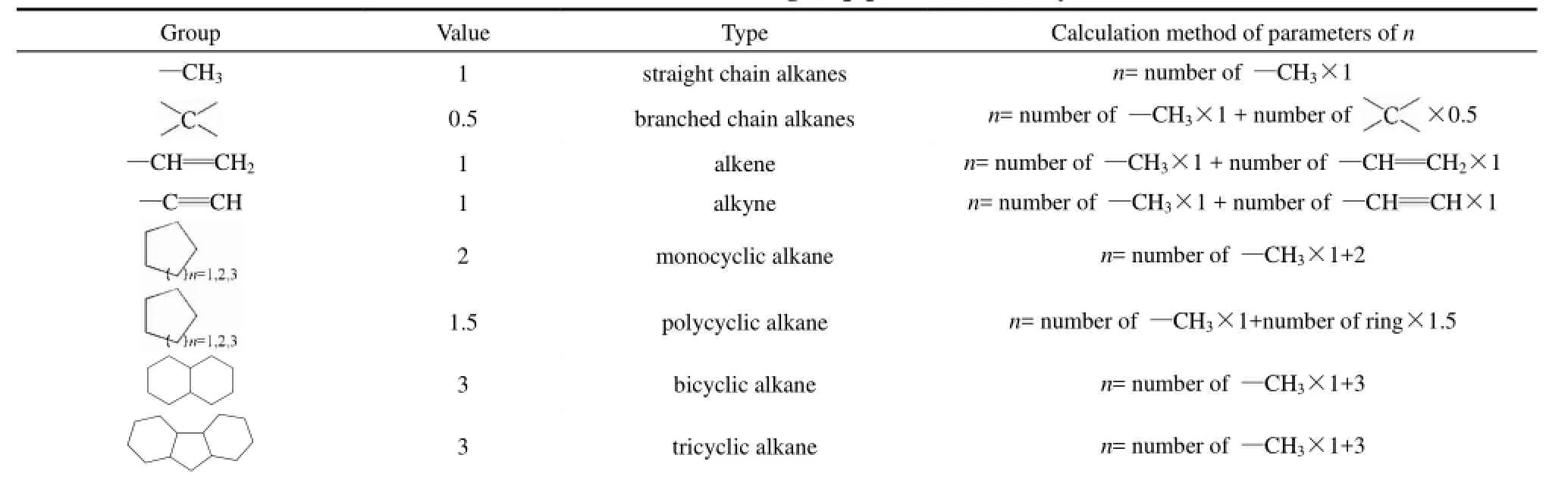
表3　烴類分子中特征基團參數n的計算方法Table 2 Calculation methods of n values for group parameters of hydrocarbon molecules

1.4 分子結構固有頻率計算

從文獻[22]可知，多自由度振動體系的特征方程為

由此方程計算 p2的n個正實根p2i，并按 pi≤ pi+1(i=1,2,…,n)排列。pi稱為系統的固有頻率，其中不等于零的最小固有頻率稱為基頻。式(3)中的K是分子結構體系的整體剛度矩陣，M是分子結構體系的集中質量矩陣，即由隱氫分子圖中各原子基團的質量構成。固有頻率的計算可直接調用MATLAB程序代碼“eig”求解，即

根據以上方法計算得到 78個烴分子固有頻率pi和各階固有頻率之和(∑pi)的值。

1.5 分子結構特征基團參數n的定義與計算

對78個烴分子的581個熱導率實驗數據的回歸分析發現，同系列烴分子中某些特征基團可具有相同的取值，如分子中的甲基可取值為 1，季碳原子可取值為0.5，端基烯、炔鍵可取值為1，單環烷烴中的環結構可取值為 2，多環烷烴的環結構可取值為1.5，分子中的十氫化萘、芴結構可取值為3。特征基團參數n的定義、取值及計算方法列于表2。

特征基團參數n的計算方法如下所示。

（1）烷烴:在烷烴分子中，只有甲基—CH3和碳鏈中季碳原子作為分子中的特征基團，其余碳鏈中間的—CH2—，碳原子不是特征基團，其結構特征在鍵長數據L中已經表征。特征基團參數n的計算方法如下。

例1:2,2,5,5-四甲基己烷，分子含6個甲基，2個季碳原子，其特征參數n值的計算結果為

（2）烯烴:只有處于端基的烯鍵—CH═CH2符合特征基團，不處于鏈端的雙鍵結構不屬于特征結構，其結構特征在鍵長數據L中已經表征。

例2:2-甲基-1,3-丁二烯分子，雖然有兩個烯鍵，但只有1個烯鍵符合，所以對應的特征參數n值僅由1個甲基數和1個烯鍵數來確定，即

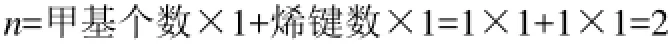
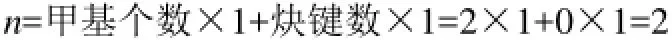
（4）環烷烴:分子中的單環結構均作為特征基團計算。

例 4:乙基環己烷分子，分子中的特征基團為1個甲基，1個C6環，特征基團參數n為

（5）環烴:

例5:以雙-(2,4,6-環己基)甲烷分子為例，分子中的特征基團有6個甲基，2個環己基，所以該分子的特征基團參數n值為9，即

（6）復雜烷烴:特征基團包括表2列出的8類結構的一種或幾種。

例6:α-甲基十氫化萘分子中有1個甲基和1個十氫化萘環結構，特征基團參數n計算如下

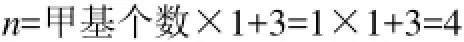
1.6 QSPR模型的建立

最佳子集回歸算法(best subsets regression)是尋找特定數目自變量組合中最佳的一種或幾種搭配的多元線性回歸方法。可以根據使用者設定的條件選擇含有1，2，3，…，n個變量的最佳變量組合。該方法可以逐步考察不同變量組合對因變量的影響。因此本文采用最佳子集回歸算法篩選參數并建立多元線性回歸(multiple linear regression，MLR)方程。

1.6.1 熱導率與溫度的關系 由于分子的熱導率與溫度的關系非常密切，在建立QSPR模型時既要考慮分子結構的影響，也要考慮到溫度的影響。文獻[12]對于熱導率與溫度的關系作了專門研究，得到的關聯方程為

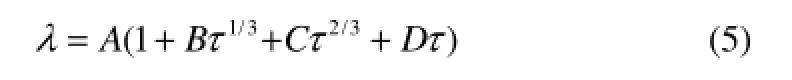
式中，τ=1-T/Tc，這里的Tc是臨界溫度，A是臨界熱導率，B、C、D是常數。由此可以看出，溫度對液體熱導率的關系是一種非線性關系。由于式(5)的表達依賴于臨界溫度，本文并不直接將該式引入QSPR模型，而是曲線擬合，發現烴類液體熱導率受溫度影響的函數表達式可歸結為

式中，T是熱力學溫度，a為回歸常數，b、c為參數的回歸系數。1.6.2 結構參數篩選及QSPR方程建立 將前文得到結構參數∑pi,δm,n,以及其他結構參數組成參數集，將化合物300 K熱導率作為因變量，通過最佳子集回歸方法篩選分子結構參數，得到固有頻率之和∑pi(簡稱總頻)、整體剛度矩陣平均絕對特征值δm及組成的最佳3參數回歸方程式(7)

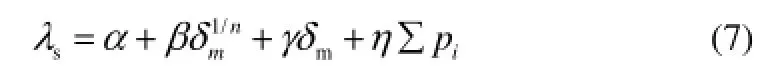
再考慮溫度對熱導率的影響，將式(6)和式(7)合并，得到式(8)

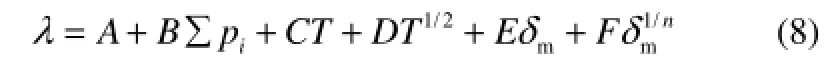
式(8)為本文建立的多類烴液體熱導率的QSPR模型。

2　結果與討論

2.1 模型的擬合

本文從文獻[24]收集了多類烴(直鏈烷烴分子20個，支鏈烷烴分子20個，烯烴分子4個，炔烴分子3個，環烷烴分子18個，萘烷分子12個，芴分子1個)的581個液體熱導率實驗數據，作為訓練集，擬合QSPR方程式(8)，得到最終的熱導率QSPR方程式(9)

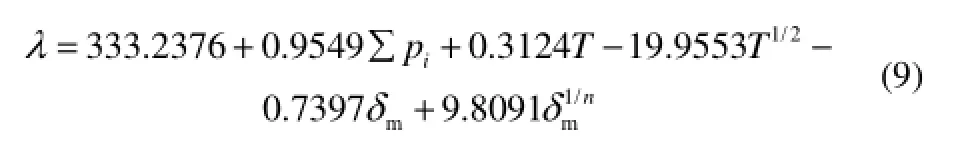
(train set: n=581, R=0.9874, s=3.45, F=4483;

test set: n=22, R=0.9550, s=4.42, F=207)

根據式(9)計算得到 581個化合物的熱導率數據，該方程對581個訓練集熱導率的計算值與實驗值的相關系數為0.9874，平均相對誤差為2.39%。實驗值與計算值的相關性如圖1所示。從圖1可以看出，實驗值和計算值數據點分布基本在對角線上，表明實驗值和計算值基本一致。

圖1　熱導率計算值與實驗值比較Fig.1 Plot of experimental λexp.versus calculated λcalc.

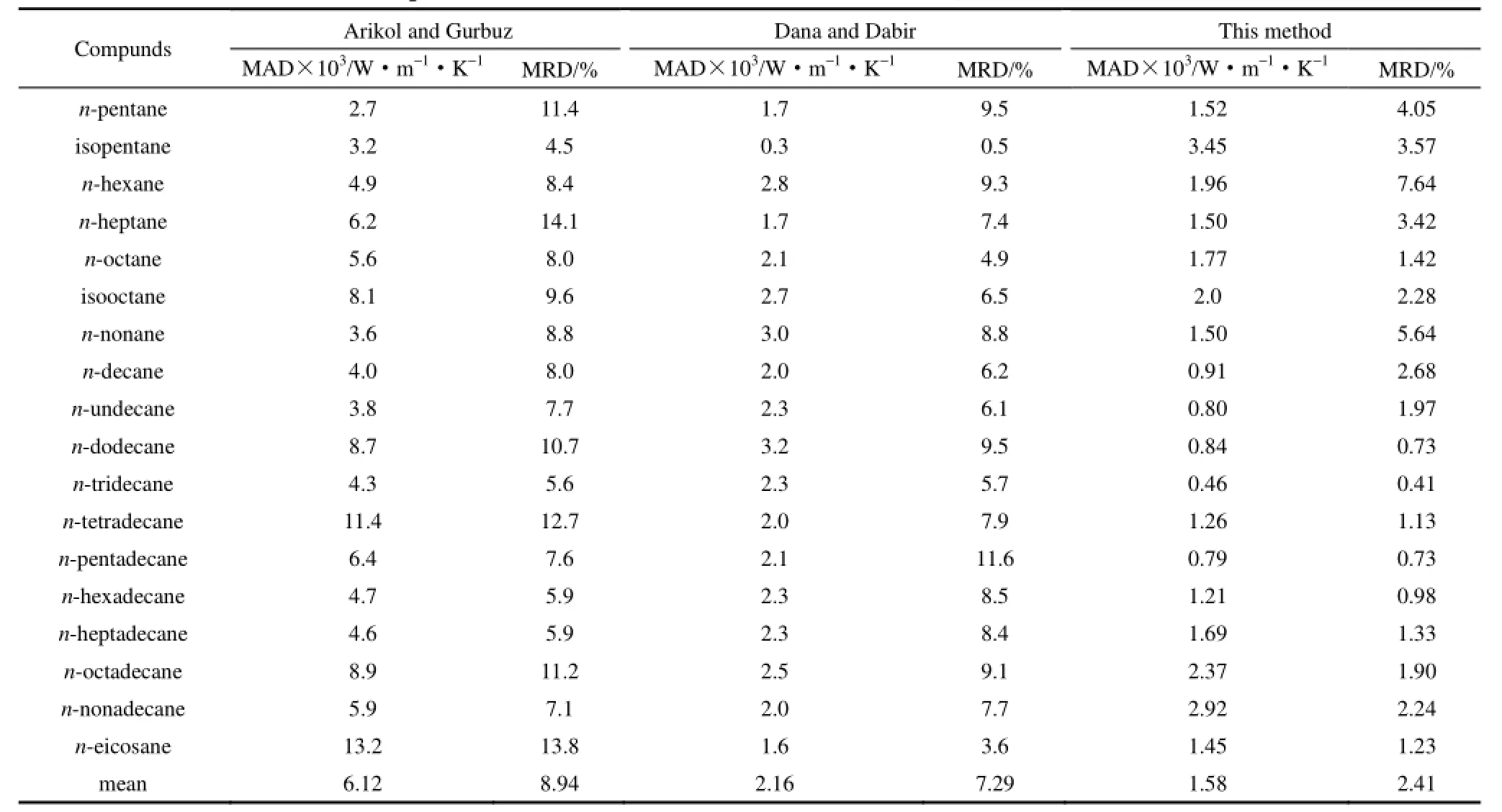
表3　Arikol and Gurbuz, Dana and Dabir和本文方法預測結果的比較Table 3 Comparison of new method with Arikol and Gurbuz, Dana and Dabir methods

2.2 模型方程的檢驗和方程預測性能力分析

為了進一步驗證模型(9)預測能力，從文獻[24]收集22個烴的液體熱導率數據作為測試集，用式(9)預測了這些物質的熱導率，預測值和實驗值的相關系數R=0.9550，平均相對誤差為2.42%。預測結果在實驗值的誤差范圍之內(5%)。預測值和實驗值的比較如圖1所示。說明式(9)具有良好的預測能力。

2.3 估算結果比較

為了考察本文方法與已有方法的優劣，隨機選取了18個烴，用不同的方法計算這些有機物的熱導率。一種方法為Arikol等[10]提出的熱導率關聯式，該關聯式在已知溫度、臨界溫度、臨界壓力、分子量和標準沸點的條件下，計算了液體熱導率。另一方法是Dana等[11]提出的熱導率關聯式。表3同時列出了Arikol、Dana和本文方法的計算結果。

從表3可以看出，本文提出的計算方程的平均絕對誤差為0.00158 W·m-1·K-1，平均相對誤差為 2.41%；Arikol 和Gurbuz法[10]的平均絕對誤差為0.00612 W·m-1·K-1，平均相對誤差為8.94%；Dana和 Dabir法[11]的平均絕對誤差為 0.00216 W·m-1·K-1，平均相對誤差為 7.29%。本文方法計算結果明顯優于其他兩種方法。特別是平均相對誤差優勢更為明顯。同時表 3的數據中，正辛烷(n-octane)和異辛烷(isopentane)兩個烷烴不在本文的訓練集樣本中，是擬合集以外的預測結果。式(9)對正辛烷的預測結果明顯優于其他兩種方法的估算結果。對異戊烷所產生的絕對誤差與Arikol和Gurbuz法接近，相對誤差仍然小于 Arikol和Gurbuz法，但比Dana和Dabir法的誤差略大。

2.4 熱導率的影響因素

2.4.1 特征基團對液態烴熱導率的影響 在式(9)中，對指數項的回歸系數為9.8091，由于平均絕對特征值(δm)總是大于1的數值。因此，所有增加n值的因素都使得指數項的值變小，說明用振動力學有限元方法提取的結構參數δm高估了液態烴分子的熱導率，必須通過指數項(1/n)來加以修正。

2.4.2 甲基的影響 在以化學鍵空間剛架元為結構單元提取分子結構特征參數時，落在節點處的基團可分為兩種類型，一類是化學鍵的端點，另一類是兩個或兩個以上化學鍵的連接點。對于烴分子而言，甲基屬于端點基團，由于有一端與另一化學鍵連接，除了振動以外，還可以發生轉動，這種轉動不利于分子間熱量傳導，同時相同碳原子數的分子，甲基越多，支鏈越多，分子主鏈越短，影響了分子能量傳遞效率。因此，分子中的甲基數越多，與碳原子數相同的直鏈烴比較，其熱導率越小。如正癸烷在320 K時的液體熱導率值為0.125 W·m-1·K-1，而 2,2,5,5-四甲基己烷的液體熱導率值為 0.092 W·m-1·K-1。

3　結 論

本文用振動力學有限元分析方法，提取的分子結構特征參數和基團特征參數能定量地表達分子結構對多類液態烴熱導率的影響規律。得到的定量構效關系方程為:λ=333.2376+0.9549∑pi+0.3124T-19.9553T1/2-0.7397δm+9.8091。

該方程適用于從鏈烷烴、烯烴、炔烴到單環烷烴、多環烷烴、十氫化萘類、芴烷類、茚烷類、菲烷類、蒎烷類等復雜結構烴類的液態熱導率的估算。方程中的結構參數固有頻率 pi和平均絕對特征值δm，無須依賴其他實驗數據或臨界參數。用固有頻率和剛度矩陣特征值作為結構參數來定量描述分子的液體熱導率隨分子結構不同的變化規律，與物質通過內部原子、分子的振動和相互碰撞進行熱量傳導的導熱機理吻合。同時在方程中引入分子結構特征基團參數n的意義重大，它不僅揭示了分子結構的差異對分子宏觀性能的影響，而且擴大了預測方程的適用范圍，使估算方程可以推廣到其他復雜有機分子液體熱導率的預測，為工程應用中熱導率數據提供了比較可靠的計算方法。

References

[1] DRAGHI N C, FAYET G, CRETON B, et al. A general guidebook for the theoretical prediction of physicochemical properties of chemicals for regulatory purposes[J]. Chem. Rev., 2015, 115(24): 13093-13164.

[2] SASTRI S S, RAO K K. A new temperature-thermal conductivity relationship for predicting saturated liquid thermal conductivity[J]. Chem. Eng. J., 1999, 74(3): 161-169.

[3] PATEL N C, TEJA A S. A new cubic equation of state for fluids and fluid mixtures[J]. Chem. Eng. Sci., 1982, 37(3): 463-473.

[4] CHEN Q L, WU K J, HE C H. Thermal conductivity of ionic liquids at atmospheric pressure: database, analysis, and prediction using a topological index method[J]. Ind. Eng. Chem. Res., 2014, 53(17): 7224-7232.

[5] HEZAVE A Z, RAEISSI S, BOLOOKI M L. Estimation of thermal conductivity of ionic liquids using a perceptron neural network[J]. Ind. Eng. Chem. Res., 2012, 51(29): 9886-9893.

[6] CARRETE J, TRINIDAD M M, MANUEL G, et al. Thermal conductivity of ionic liquids: a pseudolattice approach[J]. J. Phys. Chem., 2012, 116(1): 1265-1273.

[7] LAZZúS J A. A group contribution method to predict the thermalconductivity λ(T,P) of ionic liquids[J]. Fluid Phase Equilibria, 2015, 405(11): 141-149.

[8] POLING B E, PRAUSNITZ J M, CONNELL J P. The Properties of Gases and Liquids[M]. 5th ed. Boston: The McGraw-Hill Companies, Inc., 2001: 420-436.

[9] WATANABE H, KATO H. Thermal conductivity and thermal diffusivity of twenty-nine liquids: alkenes, cyclic (alkanes, alkenes, alkadienes, aromatics), and deuterated hydrocarbons[J]. J. Chem. Eng. Data, 2004, 49(4): 809-825.

[10] ARIKOL M, GURBUZ H. A new method for predicting thermal conductivity of pure organic liquids and their mixtures[J]. Can. J. Chem. Eng., 1992, 70(6): 1157-1163.

[11] DANA M K, DABIR S V. A correlation for the prediction of thermal conductivity of liquids[J]. Ind. Eng. Chem. Res., 1998, 37(5): 2064-2068.

[12] JAMLESON D T. Thermal conductivity of liquids[J]. J. Chem. Eng. Data, 1979, 24(3): 244-246.

[13] JAMIESON D T, CARTWRIGHT G. A correlation for the prediction of thermal conductivity of liquids[J]. J. Chem. Eng. Data, 1980, 25(3): 199-201.

[14] 張克武, 張玉英. 液體烴的分子結構與導熱率[J]. 化工學報, 1999, 50(2): 247-252.

ZHANG K W, ZHANG Y Y. Extended application of TENSG on thermal conductivity and molecular structure of liquid hydrocarbons [J]. Journal of Chemical Industry and Engineering (China), 1999, 50(2): 247-252.

[15] 仇明華, 曹晨忠. 液體鏈烷烴熱導率與分子結構的關系[J]. 湘潭大學自然科學學報, 2002, 24(3): 69-73.

QIU M H, CAO C Z. Relationship between the thermal conductivity of liquid alkane and it’ s molecular structure[J]. Natural Sci. J. Xiangtan University, 2002, 24(3): 69-73.

[16] 高碩, 曹晨忠. 拓撲量子方法估算液體鏈烷烴熱導率[J]. 物理化學學報, 2006, 22(16): 1478-1483.

GAO S, CAO C Z. A topological quantum method for the estimation of the thermal conductivity of liquid alkanes[J]. Acta. Phys. Chim. Sin., 2006, 22(16): 1478-1483.

[17] 彭國文, 肖方竹, 聶長明, 等. 液相鏈烷烴熱導率與其結構定量關系[J]. 化工學報, 2011, 62(3): 604-610.

PENG G W, XIAO F Z, NIE C M, et al. Quantitative relationship between thermal conductivity and structure of liquid alkanes[J]. CIESC Journal, 2011, 62(3): 604-610.

[18] 萬麗華, 梁德青, 吳能友, 等. 客體分子數對甲烷水合物導熱性能影響的分子動力學模擬[J].化工學報, 2012, 63(2): 382-386.

WAN L H, LIANG D Q, WU N Y, et al. Molecular dynamics simulation of gest molecule number on methane hydrate thermal performance[J]. CIESC Journal, 2012, 63(2):382-386.

[19] 萬麗華, 梁德青, 關進安. 烴類水合物導熱特性的分子動力學模擬[J]. 化工學報, 2014, 65(3): 792-796.

WAN L H, LIANG D Q, GUAN J A. Characteristic of thermal conduction in hydrocarbon hydrates using molecular dynamics method[J]. CIESC Journal, 2014, 65(3): 792-796.

[20] 馬慶芳. 傳熱學[M]. 北京: 人民教育出版社, 1976.

MA Q F. Heat Transfer [M]. Beijing: People’s Educational Press, 1976.

[21] 劉延柱. 彈性細桿的非線性力學—DNA力學模型的理論基礎[M].北京: 清華大學出版社, 2006.

LIU Y Z. Nonlinear Mechanics of Thin Elastic Rod: Theoretical Basis of Mechanical Model of DNA[M]. Beijing: Tsinghua University Press, 2006.

[22] 方同, 薛璞. 振動理論及應用[M]. 西安:西北工業大學出版社, 2002: 99.

FANG T, XUE P. Vibration Mechanics and Application[M]. Xi’an: NWPU Press, 2002: 99.

[23] KATTAN P I. MATLAB Guide to Finite Element Analysis[M]. Berlin: Springer-Verlag, 2003.

[24] VARGAFTIK N B, FILIPPOV L P, TARZIMANOV A A, et al. Handbook of Thermal Conductivity of Liquids and Gases[M]. Boca Raton FL: CRC Press, 1994.

2015-10-13收到初稿，2016-01-23收到修改稿。

聯系人:劉萬強。第一作者:仇明華(1958—)，男，教授。

Received date: 2015-10-13.

中圖分類號:O 642.1；TQ 013.1

文獻標志碼:A

文章編號:0438—1157（2016）07—2672—07

DOI:10.11949/j.issn.0438-1157.20151546

基金項目:國家自然科學基金項目(21472040, 21202043)；湖南省教育廳科學研究項目（13C302）。

Corresponding author:LIU Wanqiang,wanqiangliu@foxmail.com supported by the National Natural Science Foundation of China (21472040, 21202043) and the Science Research Project of Hunan Provincial Department of Education(13C302).

Conductivity estimates of liquid hydrocarbons by finite element analysis in vibration mechanics

QIU Minghua1,2, LIU Wanqiang1,2, CHEN Guanfan1, LIU Fengping1, YUE Ming1
(1School of Chemistry and Chemical Engineering, Hunan University of Science and Technology;2Key Laboratory of Theoretical Organic Chemistry and Functional Molecule, Ministry of Education, Xiangtan 411201, Hunan, China)

Abstract:Given hydrocarbon molecular structures as elastomers, three dimentional (3D) molecular structure of hydrocarbons was analyzed by finite element analysis in vibration mechanics. The stiffness matrix and vibration equation of molecular structure system was established, and its eigen values of inherent frequency and stiffness matrix were obtained by calculation using MATLAB software, followed by QSPR model for the liquid hydrocarbon conductivity by multivariate regression method. For training set consisting of 581 liquid hydrocarbons, the correlation coefficient R between the calculated values of liquid conductivity using QSPR model and the experimented data is 0.9874, the mean absolute error less than 0.00259 W·m-1·K-1, and the relative error less than 2.39%. For testing set comprising 22 liquid hydrocarbons, the correlation coefficient R is 0.9550, the mean absolute error less than 0.00263 W·m-1·K-1, and the relative error less than 2.42%. It showed that the calculated values by this QSPR model fit experimental data well in terms of conductivity of liquid hydrocarbon. It can be used to estimate the liquid conductivity of complex hydrocarbons such as acyclic alkanes, alkenes, alkynes, monocycle alkanes, polycyoalkanes, decahydronaphthalenes, fluorene alkanes, perhydrophenanthrenes, indene alkanes, and pinanes.

Key words:conductivity; heat conduction; thermodynamic properties; molecular structure descriptor; finite element analysis