基于均衡系數的決策樹優化算法

董躍華　劉　力

1(江西理工大學信息工程學院　江西 贛州 341000)2(江西理工大學計算機科學與技術系　江西 贛州 341000)

?

基于均衡系數的決策樹優化算法

董躍華1劉力2

1(江西理工大學信息工程學院江西 贛州 341000)2(江西理工大學計算機科學與技術系江西 贛州 341000)

摘要針對ID3算法多值偏向及誤分類代價被忽視的問題，結合屬性相似度和代價敏感學習，提出基于均衡系數的決策樹優化算法。該算法既克服了多值偏向，又考慮了誤分類代價問題。首先引進屬性相似度和性價比值兩者的均衡系數，對ID3算法進行改進；然后運用麥克勞林公式對ID3算法進行公式簡化；最后將算法改進和公式簡化相結合，得到基于均衡系數的決策樹優化算法。實驗結果表明，基于均衡系數的決策樹優化算法，既能夠提高分類精度，縮短決策樹生成時間，又能考慮代價問題并降低誤分類代價，還能克服多值偏向問題。

關鍵詞ID3算法屬性相似度代價敏感學習決策樹均衡系數

0引言

數據分類是數據挖掘中重要的研究方法之一，其中有決策樹分類器、貝葉斯分類器等基本技術。目前各類決策樹算法中，ID3算法的影響最大，但ID3算法存在多值偏向等問題。針對ID3算法的多值偏向問題，自Quinlan提出C4.5算法[1]以來，許多學者進行相關的改進工作：文獻[2]根據概率統計中條件概率的大小劃分屬性；文獻[3,4]選取關聯度值最大的屬性作為分裂屬性；文獻[5-8]將粗糙集理論中的屬性重要度或屬性依賴度作為選擇分裂屬性的標準；文獻[9,10]將屬性相似度作為選擇分裂屬性的標準。在一定程度上，文獻[2-10]引入新的屬性分裂標準雖能克服多值偏向，但新的選擇標準意味著會涉及統計學、粗糙集等其他領域知識，因為其不同于信息熵理論的計算方式，所以在分類準確率上會低于ID3算法。

針對ID3算法忽視因誤分類而產生的代價問題，除了近來一些學者將誤分類代價最小化作為分類效果新的衡量標準，并提出代價敏感學習CSL(Cost-Sensitive Learning)[11]之外，相關學者也進行了一些研究工作：文獻[12]在CSL的基礎上，提出基于誤分類代價和測試代價的決策樹算法，該算法雖考慮了代價問題，但卻忽視屬性自身的分類能力；文獻[13,14]在文獻[12]的基礎上進行改進，提出了基于代價問題與信息熵公式相結合的決策樹算法，該算法雖兼顧了代價問題和屬性自身的分類能力，但仍存在多值偏向問題。

本文在文獻[9]和文獻[14]的基礎上,結合屬性相似度和代價敏感學習，提出了基于均衡系數的決策樹優化算法，通過引入屬性相似度和性價比值兩者的均衡系數，對ID3算法改進。實驗結果表明，基于均衡系數的決策樹優化算法，能夠克服多值偏向問題，提高分類精度，兼顧代價問題并降低誤分類代價。

1ID3算法

1.1ID3算法的基本思想

設訓練集S有s個樣本，將訓練集分成m個類，第i類的實例個數為si。選擇屬性Ai劃分訓練集S，設屬性Ai有屬性值{S1，S2，…，Sj，…，Sk}，Sj中屬于第i類的訓練實例個數為sij，則得到劃分屬性Ai的信息增益為[15]：

Gain(Ai,S)=Info(S)-InfoAi(S)

(1)

其中：

(2)

(3)

(4)

其中，pi為S中屬于第i類的概率，pi=si/s；pij為sj中第i類樣本的概率，pij=sij/sj。

1.2ID3算法的缺陷

ID3算法雖是常用的分類算法，但其仍存在一些缺陷：

(1) 信息熵的計算方式使ID3算法的屬性選擇容易偏向于取值較多的屬性，但有較多屬性值的屬性不一定是當前最佳分裂屬性；

(2) 分類過程中存在誤分類情況，而ID3算法卻忽視了因誤分類而產生的代價問題[16]；

(3) 數據集中樣本數增多時，算法對應計算量的增長幅度變大。

針對ID3算法的缺陷，可在多值偏向、誤分類代價、信息熵公式簡化方面對ID3算法進行改進。

2ID3算法相關的改進研究

針對多值偏向、誤分類代價、信息熵公式簡化這3個方面，相關專家學者對ID3算法進行改進并分別提出3種改進算法。本文的主要工作即為：通過研究3種改進算法的優缺點，尋找一種新的改進算法，使新的改進算法在繼承3種改進算法優點的同時，也要克服其不足之處。

2.1針對多值偏向的ID3算法改進

文獻[9]提出基于屬性相似度的決策樹改進算法，并表明將屬性相似度作為屬性選取標準可克服多值偏向問題。

2.1.1基于屬性相似度的決策樹改進算法的原理

文獻[9]中參照知識粒度[17]的定義將條件屬性Ai與決策屬性D的屬性相似度定義為：

(5)

其中Ai為條件屬性集合C中的元素，C為：C={A1,A2,…,Ai,…,An}，D為決策屬性集合：D={D1,D2,…,Dm}。元素fi，j表示屬性Ai中屬于Dj類樣本個數，可用m+1行n+1列矩陣表示，矩陣中第j行第n+1列表示決策屬性Dj的總樣本個數，第m+1行第i列表示屬性Ai的總樣本個數。

式(5)中屬性相似度值S(D,Ai)的大小表示條件屬性Ai與決策屬性D之間相似度程度的大小。

2.1.2基于屬性相似度的決策樹改進算法的不足

(1) 因屬性相似度脫離信息熵理論而導致其在分類準確率上低于ID3算法。

(2) 未考慮因誤分類而產生的代價問題。

2.2針對誤分類代價的ID3算法改進

文獻[14]提出一種基于代價敏感學習的決策樹改進算法，該算法將信息熵理論與代價敏感學習相結合，在繼承ID3算法較高分類準確率的同時，也考慮了誤分類代價問題。

2.2.1基于代價敏感學習的決策樹改進算法的原理

若選擇Ai作為分裂屬性且當前決策樹結點Node為正例結點，裂后有n個子屬性{S1,S2,…,Si,…,Sn}，對應n個子節點(Node1,Node2,…,Nodei,…,Noden,),子結點Nodei包含xi個正例和yi個反例，令前r個子結點為正例結點，后(n-r)個子結點為反例結點[18]。屬性Ai的代價性能比值Cost_ratio(Ai)定義為[19]：

(6)

其中，Cost(Ai)為Ai未分裂時當前結點Node的誤分類代價；FP為錯誤正例造成的誤分類代價，FN為錯誤反例所造成的誤分類代價，T_Cost(Ai)為獲取屬性Ai信息時所需付出的測試代價，分母加1是為防止某個屬性測試代價為0時而導致計算錯誤出現。

2.2.2基于代價敏感學習的決策樹改進算法的不足

該算法仍存在公式計算量較為龐大的問題以及多值偏向的問題。

2.3針對信息熵公式簡化的ID3算法改進

文獻[20,21]通過運用等價無窮小的方式，令ID3算法公式中的log對數運算轉變為四則運算，以達到簡化信息熵公式的目的。

2.3.1信息熵公式簡化的原理

含拉格朗日型余項的麥克勞林公式定義為[22]：

(7)

由此得到近似公式：

(8)

由此可得：

(9)

當x趨向于0時，可得等價無窮小變換：

ln(1+x)～x

2.3.2等價無窮小簡化信息熵公式的不足

當自變量必須趨向于0時，才可使用等價無窮小進行等價變換。當自變量不趨向于0時，使用等價無窮小變換會導致簡化后的公式比原信息熵公式的精度低。

3基于均衡系數的決策樹優化算法

3.1基于均衡系數的決策樹優化算法的思路

3.1.1改進基于屬性相似度和代價敏感學習決策樹算法的不足

基于屬性相似度的決策樹改進算法可克服多值偏向問題；基于代價敏感學習的決策樹改進算法可克服因脫離信息熵理論而導致分類準確率低下的問題，也能克服誤分類代價被忽略的問題，因而將兩種決策樹改進算法相結合可彌補兩者自身的不足。本文通過運用等效電阻原理，將文獻[9]的屬性相似度和文獻[14]的代價性能比值相結合得到新的指標系數——均衡系數，均衡系數能夠同時繼承兩種決策樹改進算法的優勢，因而能夠同時兼顧多值偏向和誤分類代價被忽視問題。最后將均衡系數引入信息熵公式以完成對ID3算法的改進。

3.1.2改進等價無窮小簡化信息熵公式的不足

當自變量不會趨向于0時，使用等價無窮小變換會導致簡化后的公式精度降低。信息熵公式的值的大小在0和1之間，因而在式(9)的基礎上可得：

當x∈(0,1)時：

(10)

通過運用公式(10)對信息熵公式中的對數運算進行近似轉換，以完成信息熵公式的簡化。

3.1.3DTEC算法

本文針對“多值偏向、誤分類代價被忽視問題”和“信息熵計算公式”兩個方面，將改進基于屬性相似度和代價敏感學習決策樹算法的不足、改進等價無窮小簡化信息熵公式的不足兩部分的工作相結合，分別對ID3算法進行算法改進和公式簡化，提出了基于均衡系數的決策樹優化算法，簡稱DTEC算法。

3.2ID3算法的改進

3.2.1均衡系數的引入1) 代價性能比值的改進

誤分類代價為專家給的相對值，測試代價多以貨幣為單位，代價性能比值中分子與分母兩者的值域顯然不在同一范圍，這會導致比值不準確并產生誤差。為克服該問題，可采用規范化方法對性能比值進行改進，將測試代價規范化至誤分類代價的取值區間，規范化后的測試代價為T_NewCost(Ai)：

(max[Cost(Ai)]-min[Cost(Ai)])+min[Cost(Ai)]

(11)

則改進后的代價性能比值New_Cost_ratio(Ai)為：

(12)

式(12)中的分子和分母已處于同一數量級，可避免出現比值結果偏向分子和分母中數量級較大者的數量級偏向問題。

2) 均衡系數的引入

電路中有等效電阻原理：電阻R1和R2并聯，等價于串聯入等效電阻R′。電阻R1、R2、R′兩端電壓均為U，通過電流分別為IR1、IR2、IR′。由此可推導出如下關系：

(13)

屬性相似度和性價比值分別對應電阻R1和R2，均衡系數對應電阻R′，運用等效電阻原理可將本文提出的均衡系數R(Ai)可定義為：

(14)

均衡系數R(Ai)的作用效果，等效于屬性相似度和性價比值兩者指標盡可能取較優值，同時令兩者共同作用的效果達到最優值。

3.2.2引入均衡系數對ID3算法的改進

均衡系數對ID3算法式(1)進行改進后，得到新的信息增益式(15)：

Gain(Ai,S)New=Gain(Ai,S)×R(Ai)

=[Info(S)-InfoAi(S)]×R(Ai)

(15)

令改進后的信息增益Gain(Ai,S)new，作為屬性分裂的新標準。新的屬性分裂標準Gain(Ai,S)new既能克服ID3算法的多值偏向問題，又能使選擇的分裂屬性具有較小的誤分類代價。

3.2.3ID3算法改進后的多值偏向分析1) ID3算法多值偏向分析

(16)

由此可知式(18)的恒成立是造成多向偏值問題的本質，所以要解決多向偏值問題只要避免式(16)恒成立即可。

2) ID3算法被改進后的多值偏向分析

(17)

(18)

3.3信息熵公式的簡化

將ID3算法的信息增益公式完全展開后，變形為式(19)：

(19)

式(19)中常數m為訓練集類別數，Info(S)為一個定值，因此式(19)只保留后一項也不會影響最終比較結果，則取后一項可得式(20)：

(20)

從式(20)中可看出：對數運算是計算中主要的耗時部分，因而消去對數運算能夠降低計算量并提高計算效率。

sj中屬于第i類的訓練實例個數為sij，pij是Sj中屬于第i類的概率，pij=sij/sj，且s1j+...+smj=sj，因此式(20)可進行如下轉化：

近似式(10)比等價無窮小公式ln(1+x)≈x的精度要高。使用近似簡化式(10)可進一步化簡為：

Gain(Ai)2

ln2和樣本個數s均為常數項，去掉后不影響結果的比較，將其去掉后進一步簡化得到式(21)：

(21)

式(21)中的較為耗時的log對數運算已消除，公式完全由加減乘除四種基本運算組成，計算量降低且計算效率得到提高。

3.4DTEC算法的提出

DTEC算法包括均衡系數的引入、ID3算法改進和ID3算法公式簡化三個部分的工作，將均衡系數式(14)、ID3算法改進式(15)和ID3算法簡化式(21)相結合得到DTEC算法式(22)：

(22)

DTEC算法采用式(22)作為新的屬性選擇標準。DTEC算法既能克服多值偏向，考慮代價問題并降低誤分類代價，又能簡化ID3算法公式，降低計算量并提高計算效率。

3.5DTEC算法描述

輸入：訓練樣本集S(樣本中的屬性值均進行離散化操作),C為條件屬性集合，屬性Ai∈C；D為決策屬性集合。

輸出：DTEC決策樹。

步驟1計算條件屬性Ai與決策屬性D的屬性相似度值S(D,Ai)；

步驟2在屬性集合C中，計算屬性Ai對應的代價性能比值New_Cost_ratio(Ai)′；

步驟3計算屬性Ai對應屬性相似度和性價比值兩者的均衡系數R(Ai)；

步驟4引入均衡系數R(Ai)對ID3算法進行改進，得到屬性分裂標準Gain(Ai,S)New；

步驟5利用麥克勞林展開式對ID3算法公式進行簡化，得到屬性分裂標準Gain(Ai)3；

步驟7按照式(22)分別計算各個屬性對應的熵值，選取熵值最大的屬性作為決策樹的根節點，對樣本元組進行分類。對分類后形成的子集，用遞歸的方法，計算熵值并按照熵值的大小進行屬性分裂，直到DTEC決策樹構建完成。

4實驗及結果分析

4.1實驗環境

4.1.1實驗采用工具

1) 實驗采用的數據集

本實驗在標準數據集UCI上進行，采用UCI提供的若干個標準數據集(如表1所示)進行數據分析。

表1　數據集

2) 實驗采用的實例訓練集

采用商務購車顧客數據庫(如表2所示)作為訓練集D，對數據進行選取、預處理和轉換操作后得到樣本集合，該集合包含4個條件屬性：喜歡的季節(含4個屬性值：春天、夏天、秋天、冬天)、是否商務人士(含2個屬性值：是、否)、收入(含3 個屬性值：高、中、低)、駕車水平(含2 個屬性值：良好、一般)。樣本集合根據類別屬性“是否買車”(含有 2 個屬性值：買、不買)進行劃分。

表2　商務購車顧客數據庫訓練集D

3) 實驗采用平臺

本實驗采用WEKA平臺，WEKA是一款免費且基于JAVA環境下開源的機器學習以及數據挖掘軟件。由于WEKA屬于開源軟件，WEKA中的ID3算法位于weka.classifiers.trees包中，因此改進后的ID3算法只要符合其接口規范，就可以將新算法嵌入到WEKA中并調試運行。

本實驗將ID3的WEKA源代碼導入NetBeans IDE 8.0 RC中并添加DTEC算法源代碼，然后在NetBeans IDE 8.0 RC中分別編譯ID3算法和DTEC算法程序。

4) 實驗采用設備配置

實驗所采用計算機配置為：CPU為酷睿i5 2300系列，主頻為2.8GHz，內存為4G，操作系統為Win 7。

5) 實驗采用仿真軟件

本實驗將Matlab 2012a作為繪圖仿真軟件。

4.1.2實驗初始條件

(1) 將表1數據集中2/3的樣本作為訓練集，1/3的樣本作為測試集，采用文獻[24]中的方法對數據集中連續性屬性進行離散化操作。

(2) 令各個數據集處在相同的軟硬件環境下，并使各個數據集的測試代價都相同。

(3) 分類準確率實驗評價標準

分類準確率是分類問題中常用的評價標準，能體現出分類器對數據集的分類性能。分類準確率指分類器中被正確分類的樣本個數在總的檢驗集中所占比例[25]，定義為式(23)：

(23)

其中s為總的樣本個數，m為分類類別個數，si為訓練集中屬于第i類的實例個數。

(4) 誤分類代價實驗評價標準

評定標準：使用誤分類代價比值w進行評價。誤分類代價比值w定義為：

(24)

其中，Cost表示誤分類代價，T_Cost表示測試代價，誤分類代價比值w越大，表明在一個基本單位內的測試代價，所均分到的誤分類代價越大。同時表明當誤分類代價作為分類效果的衡量標準時，分類效果較差；當誤分類代價比值w較小時，則說明分類效果較好。

4.2DTEC算法的實例驗證與分析

以訓練集D為例，根據式(1)計算ID3算法信息增益，根據式(22)計算DTEC算法的信息增益，根據式(21)計算ID3算法公式簡化后的信息增益，最后按照決策樹建樹規則，構建各自的決策樹，分別如圖1、圖2、圖3所示。

圖1　原ID3算法生成的決策樹

圖2　DTEC算法生成的決策樹

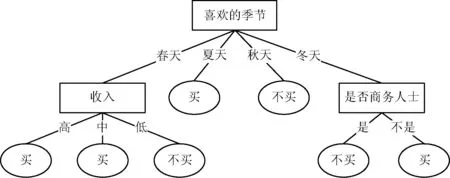
圖3　在原ID3基礎上公式簡化后生成的決策樹

圖1、圖2、圖3綜合分析發現：

(1) 比較圖1和圖2。屬性“喜歡的季節”屬性值個數最多，多值偏向使其成為決策樹的根節點。“喜歡的季節”是一種主觀想法，不是購車的決定性因素。現實生活中，“收入”在一定程度上更能決定是否購車。由圖2可看出，DTEC算法令“喜歡的季節”屬性離決策樹根結點的距離變遠，降低其重要性；令“收入”屬性作為決策樹根結點，提高其重要性，符合實際情況，因此DTEC算法在一定程度上克服了多值偏向問題。

(2) 比較圖1和圖3。由圖3可看出，ID3算法公式簡化后生成的決策樹與原ID3算法生成的決策樹完全一致。表明本文中對原ID3算法進行近似轉化的簡化公式精度較高，能夠與原ID3算法生成的決策樹基本保持一致。

4.3實驗驗證及分析

4.3.1分類準確率和葉子節點數的比較

在表2提供的數據集進行實驗數據測試，每一個數據集上進行10次試驗。在分類準確率的實驗結果中，去掉最大數據和最小數據，再求出平均分類準確率作為最終實驗數據，可使實驗結果具有普遍性。

將每一個數據集分成10個數據組，每個數據組中分別用ID3算法、C4.5算法、文獻[9]算法、文獻[14]算法和DTEC算法構建決策樹，每個數據組上均構建10次。在葉子節點數的實驗結果中，去掉最大數據和最小數據，再求出平均葉子節點數作為該數據組的最終數據。每個數據集里以數據組為最小單位進行類似操作，求出其平均葉子節點數作為該數據集的最終實驗數據。實驗結果如表3、表4所示。

表3　實驗結果一

表4　實驗結果二

從表3、表4的實驗結果中可看出:相比于ID3算法、文獻[14]算法、C4.5算法、文獻[9]算法，DTEC算法具有較高的分類準確率和較少的平均葉子節點數，并降低了構建決策樹的復雜度。

4.3.2決策樹生成時間的比較

采用實例表1中提供訓練集D，分別對ID3算法、文獻[14]算法、C4.5算法、文獻[9]算法和DTEC算法進行10次計算時間的測試,在實驗結果中去掉最大數據和最小數據，再求出平均時間作為構建決策樹所花費的時間。實驗結果如圖4所示。

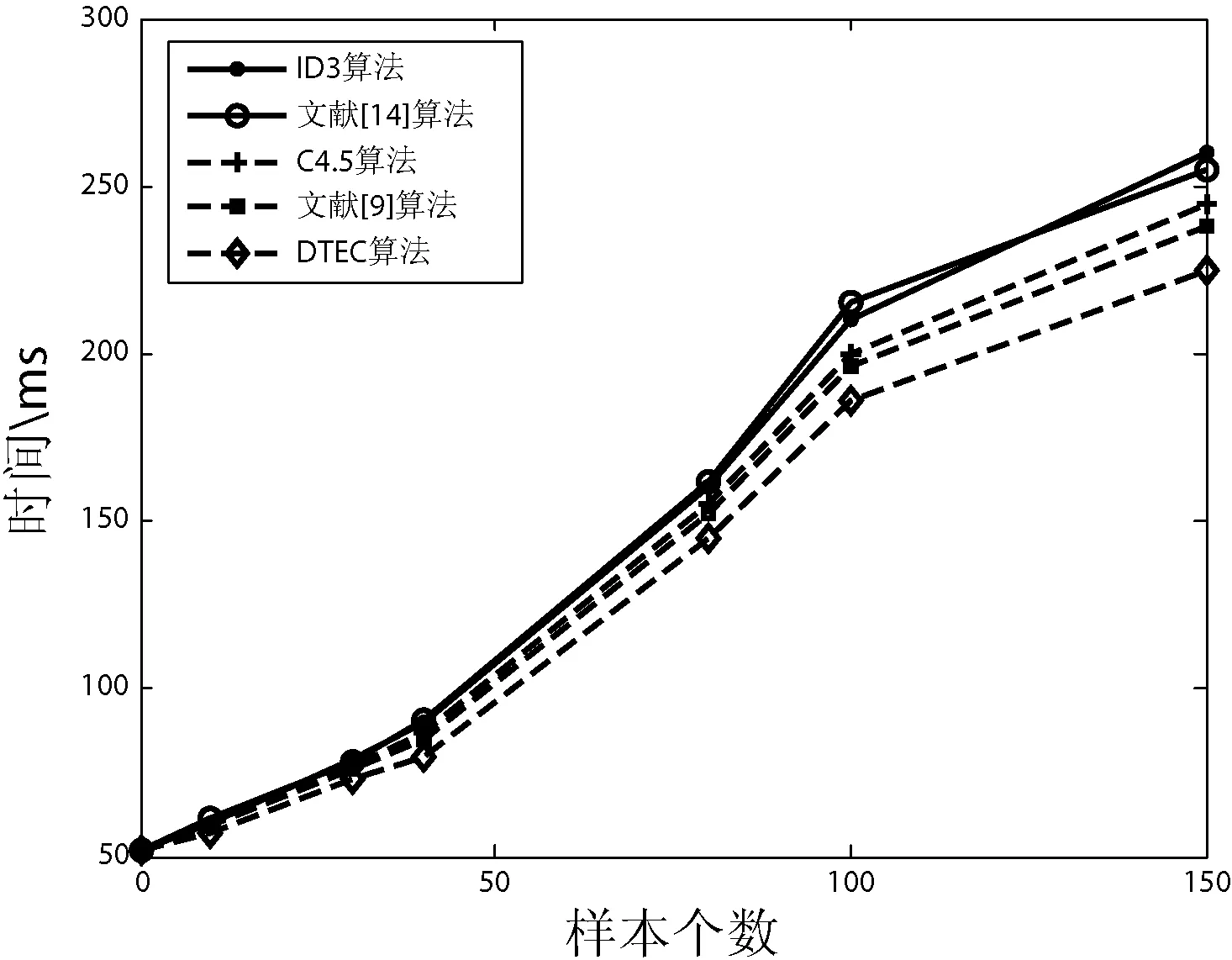
圖4　五種算法生成決策樹的時間對比

圖4中橫坐標表示訓練集樣本的取值個數，縱坐標表示構建決策樹所花費的時間。

從圖4中可看出:(1) 樣本個數偏少時，五種算法花費時間相差不大。(2) 從整體上看文獻[14]算法，所花費的時間與ID3算法的時間基本相同。(3) 當樣本個數相同時，DTEC算法構建決策樹所花費的時間最少。(4) 當樣本個數達到一定數量時，DTEC算法所節省的時間隨著樣本個數遞增而變多，這表明：在構建大規模數據集的決策樹時，使用DTEC算法能夠節約更多的時間。

4.3.3 誤分類代價的比較

以表3、表4中五種算法作為考察對象，讓每種算法按其自身的分裂屬性原則建立決策樹，最后比較它們各自產生的誤分類代價比值。實驗結果如圖5所示。

圖5　各個數據集下誤分類代價比值的對比

圖5中橫坐標表示各個數據集以及它們的名稱，縱坐標表示各個算法在不同數據集上的誤分類代價比值。

從圖5中可看出:(1)文獻[14]算法比ID3算法、C4.5算法、文獻[9]算法的誤分類代價比值都要小，當誤分類代價作為分類效果的衡量標準時，文獻[14]算法分類效果較好。(2)DTEC算法比ID3算法、C4.5算法、文獻[9]算法的誤分類代價比值都要小，但與文獻[14]算法的誤分類代價比值相差不大，當誤分類代價作為分類效果的衡量標準時，DTEC算法與文獻[14]算法分類效果近似。

4.4實驗結論

結合圖1、圖2和圖3可看出：(1) 本文提出的DETC算法能夠克服多值偏向問題；(2) DETC算法中對ID3算法公式簡化的部分，并未降低原ID3算法公式的精度，DETC算法生成的決策樹與原ID3算法生成的決策樹基本保持一致。

結合表3、表4、圖4和圖5中可看出：(1) 文獻[9]算法和C4.5算法雖然分類精度較高，決策樹建立時間較少，但未考慮誤分類代價問題，當誤分類代價作為分類效果的衡量標準時，分類效果較差；(2) 文獻[14]算法誤分類代價比值較小，雖當誤分類代價作為分類效果的衡量標準時，分類效果較好，但分類精度低，決策樹建立時間較長，此外文獻[14]算法仍存在多值偏向問題；(3) 本文提出DTEC算法，繼承了以上各個算法的長處，實驗結果分析表明：本文的優化算法具有較高的分類精度，較少的平均葉子節點數；具有較少的決策樹建立時間；考慮了代價問題并具有較低的誤分類代價比值；此外還能克服ID3算法的多值偏向問題。

5結語

針對ID3算法不足之處，結合屬性相似度和代價敏感學習提出了DTEC算法。首先，運用等效電阻原理得到屬性相似度和性價比值兩者的均衡系數，引入的均衡系數同時兼顧兩者，使屬性相似度和代價敏感學習的性價比值均較大；然后，通過引入均衡系數對原ID3算法進行改進，既克服了多值偏向問題，又兼顧了代價問題；再運用麥克勞林公式對ID3算法公式進行簡化，降低計算量并提高計算效率；最后將ID3算法的改進工作和簡化工作相結合，得到DTEC算法。實驗結果表明，本文提出的DTEC算法較之其他改進算法，不僅克服了多值偏向問題，還能考慮代價問題并降低誤分類代價，此外還具有較高的分類精度和較短的決策樹建立時間。

參考文獻

[1] 朱明.數據挖掘[M].中國科學技術大學出版社,2002:67-68.

[2] 李世娟,馬驥,白鷺.基于改進ID3算法的決策樹構建[J].沈陽大學學報:自然科學版,2009,21(6):23-25.

[3] 韓松來,張輝,周華平.基于關聯度函數的決策樹分類算法[J].計算機應用,2005,25(11):2655-2657.

[4] Jin C,Delin L,Fenxiang M.An improved ID3 decision tree algorithm[C]//Computer Science & Education,2009.ICCSE’09.4th International Conference on.IEEE,2009:127-130.

[5] 陶榮,張永勝,杜宏保.基于粗集論中屬性依賴度的ID3改進算法[J].河南科技大學學報:自然科學版,2010,31(1):42-45.

[6] 朱顥東,鐘勇.ID3算法的優化[J].華中科技大學學報:自然科學版,2010,38(5):9-12.

[7] 朱顥東.ID3算法的改進和簡化[J].上海交通大學學報,2010,44(7):883-886.

[8] 黃宇達,范太華.決策樹ID3算法的分析與優化[J].計算機工程與設計,2012,33(8):3089-3093.

[9] 陸秋,程小輝.基于屬性相似度的決策樹算法[J].計算機工程,2009,35(6):82-84.

[10] Luo H,Chen Y,Zhang W.An Improved ID3 Algorithm Based on Attribute Importance-Weighted[C]//Database Technology and Applications (DBTA),2010 2nd International Workshop on.IEEE,2010:1-4.

[11] 黃小猛.異構代價敏感決策樹與隨機森林核心技術[D].廣西師范大學,2013.

[12] Qin Z,Zhang S,Zhang C.Cost-sensitive decision trees with multiple cost scales[M]//AI 2004:Advances in Artificial Intelligence.Springer Berlin Heidelberg,2005:380-390.

[13] 覃澤,韋建忠.CSL中測試屬性選擇方法[J].微計算機信息,2008,24(6):288-289.

[14] 劉星毅.基于性價比的分裂屬性選擇方法[J].計算機應用,2009,29(3):839-842.

[15] 陳英,馬仲兵,黃敏.優化的C4.5決策樹算法[J].軟件,2013,34(2):61-64.

[16] 劉春英.基于關聯度的代價敏感決策樹生成方法[J].長春工業大學學報:自然科學版,2013,34(2):218-222.

[17] 馬福民,張騰飛.一種基于知識粒度的啟發式屬性約簡算法[J].計算機工程與應用,2012,48(36):31-33.

[18] 孟光勝.基于關聯度和代價敏感學習的決策樹生成法[J].科學技術與工程,2013,13(5):1196-1199.

[19] 阮曉宏,黃小猛,袁鼎榮,等.基于異構代價敏感決策樹的分類器算法[J].計算機科學,2013,40(11A):140-142.

[20] 喻金平,黃細妹,李康順.基于一種新的屬性選擇標準的ID3改進算法[J].計算機應用研究,2012,29(8):2895-2898.

[21] 謝妞妞,劉於勛.決策樹屬性選擇標準的改進[J].計算機工程與應用,2010,46(34):115-118.

[22] 同濟大學數學系.高等數學:上冊[M].6版.北京:高等教育出版社,2007.

[23] 張春麗,張磊.一種基于修正信息增益的ID3算法[J].計算機工程與科學,2008,30(11):46-47,94.

[24] Hu X,Cercone N.Data mining via discretization,generalization and rough set feature selection[J].Knowledge and Information Systems,1999,1(1):33-60.

[25] 武麗芬.改進的決策樹算法在文理分科中的應用研究[J].微計算機應用,2011,32(8):7-12.

收稿日期：2014-12-07。董躍華，副教授，主研領域：數據挖掘，軟件工程，軟件測試。劉力，碩士生。

中圖分類號TP301.6

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.07.061

DECISION TREE OPTIMISATION ALGORITHM BASED ON EQUILIBRIUM COEFFICIENT

Dong Yuehua1Liu Li2

1(SchoolofInformationEngineering,JiangxiUniversityofScienceandTechnology,Ganzhou341000,Jiangxi,China)2(DepartmentofComputerScienceandTechnology,JiangxiUniversityofScienceandTechnology,Ganzhou341000,Jiangxi,China)

AbstractFor the problems of ID3 algorithm in neglecting multi-value bias and misclassification cost, by combining the attribute similarity and cost sensitive learning we proposed an equilibrium coefficient-based decision tree optimisation algorithm. The algorithm solves the problem of multi-value bias and takes in to account the misclassification cost simultaneously. First, we introduced the equilibrium coefficient between attribute similarity and the value of performance to price ratio to improve ID3 algorithm. Then we used McLaughlin formula to carry out formula simplification on ID3 algorithm. Finally, we got the equilibrium coefficient-based decision tree optimisation algorithm by combining the algorithm improvement and formula simplification. Experimental results showed that the decision tree optimisation algorithm based on equilibrium coefficient can improve the classification accuracy, shorten the time of decision tree generation, and consider the cost problem as well as reduce misclassification cost. Moreover, it can also overcome the problem of multi-value bias.

KeywordsID3 algorithmAttribute similarityCost sensitive learningDecision treeEquilibrium coefficient