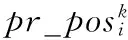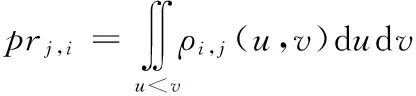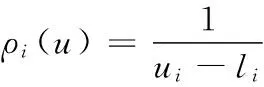基于不確定QoS的Web服務選擇

沈夢婷　劉方方

(上海大學計算機工程與科學學院　上海 200444)

?

基于不確定QoS的Web服務選擇

沈夢婷劉方方

(上海大學計算機工程與科學學院上海 200444)

摘要服務質量(QoS)是Web服務選擇的一個重要考慮因素。目前基于QoS的Web服務選擇研究多針對確定的QoS數據，此類方法不適合處理不確定的QoS屬性。而已有的針對不確定QoS屬性的研究方法基于離散的QoS屬性，無法處理QoS屬性連續時的情形。因此，提出針對不確定的連續QoS屬性的查詢方法，并提出QoS屬性值在一定分布下的優化方法。實驗表明，該方法能有效解決Web服務QoS屬性連續條件下的查詢，具備一定的可行性。

關鍵詞Web服務不確定性QoS

0引言

Internet環境下Web服務通過WSDL、SOAP和UDDI等一組技術標準進行通信。隨著Web服務技術的廣泛應用，Internet上不同的服務商提供了功能相似的Web服務。如何利用不同的QoS屬性值，從功能相似的Web服務中查找選擇高質量、滿足用戶需求的服務，已成為熱點研究問題之一。例如，通過公寓查詢服務從不同的代理上獲得一系列的價格、信譽、響應時間等租房信息，利用這些服務的QoS信息，選擇一個最能滿足用戶需求的Web服務，或通過服務排序得到最好的幾個服務。

目前對基于QoS的Web服務的研究多數是假定QoS屬性是確定的，固定不變的。例如，查詢公寓是一個單間需要998美元，這是一個固定不變的數。然而，有時價格并非是一個固定的值，可能是在一個區間里浮動，如表1所示，價格可在區間[＄990,＄1200]浮動。除了價格外，其他屬性也會在區間里浮動，比如等候申請公寓的人數較多，導致批準時間可能在1到2個月內，公寓的聲譽可能處在中等和高等之間等。以此可見，這些屬性更適合用區間表示。

在實際應用中，用確定性的方法研究Web服務往往不適用于處理不確定QoS。例如，用戶想根據價格對Web服務進行排序，而價格并非是一個確定離散的值。如表1所示，“pleasant view”的價格下界低于“sg.Court”的下界，它的上界高于后者的上界。此時QoS屬性不是離散的，因而無法用加權平均值這種計算確定QoS的方法來解決Web服務排序問題。

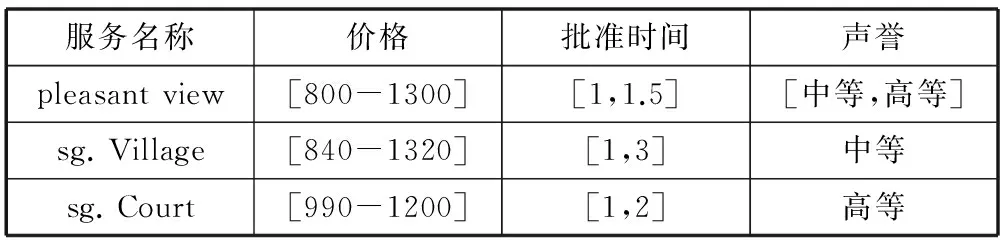
表1　租借服務

目前提出了不少針對不確定QoS的Web服務選擇的方法，而這些方法主要是在QoS屬性離散的情況下，即每個QoS值有一個存在概率。例如，響應時間1000 ms，它的存在概率是0.7。為了處理這類不確定數據，文獻[1]提出了用屬性的歷史值來統計算不確定QoS值和存在概率的方法。而文獻[2,14-17]利用skyline的方法查詢相似服務之間QoS屬性的支配關系，從而避免給QoS屬性分配權重。這些方法只考慮了QoS屬性是離散的，并沒有考慮到QoS屬性是區間值或連續的情況。

本文提出基于不確定連續QoS屬性值的Web服務選擇方法。目前，概率數據已經在數據庫領域廣泛地被研究[3-9]。對于連續性的不確定數據的研究則更具有挑戰性。其中有兩個原因:(1) 不確定數據的查詢語義并沒有統一的定義。比如，租借服務的某些提供者暫無房源時，查詢結果是否還需要選擇考慮這些服務。而在不確定數據研究中[3-9]，這些服務雖然不可用，但服務本身仍然存在，也是記錄中的一部分。由此可見，語義不同，查詢結果也會不同。(2) 對不確定數據的排序將涉及到高維概率計算，導致算法的時間消耗大。

本文針對實際應用場景，提出解決不確定QoS的Web服務查詢方法，它將不確定數據的查詢語義應用到服務查詢中。本文給出兩種查詢定義：top-uncertain 和uncertain score rank。前一種方法和U-topk[5]類似，但是U-topk只考慮離散數據，而top-uncertain是基于連續數據。后一種方法類似U-kRank的連續分布的擴展[3,4]。最后，通過實驗表明，本文提出的兩種方法能有效解決Web服務QoS屬性連續條件下的查詢，具備一定的可行性。

1查詢定義

由于Web服務處在開放的互聯網環境中， QoS受多方面影響產生不確定性。目前處理這種不確定性主要幾種在QoS離散的情況下，即計算每條記錄的存在概率，并沒考慮到QoS屬性是區間值或連續的情況。至此，本節介紹Web服務中不確定連續QoS的表示，同時介紹兩種針對QoS連續的情況下的查詢定義。

本文定義的兩種算法分別針對不同的應用場景，前者假定QoS記錄存在概率為1，即不考慮服務的可信程度；后者則假設QoS記錄有一個存在概率，主要適用于對可信度要求較高的應用場景。

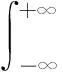
(1)其中pr(sj)表示Web服務sj的存在概率。式中，它由各個屬性的存在概率決定。例如，由于受網絡的影響，Web服務的響應時間會出現波動，同時服務被客戶正確使用的概率，即可用性也會隨著時間的變化不斷改變。區間表示集中出現的波動范圍，每個屬性的浮動區間存在一個概率密度函數。一個Web服務的可信概率，也即存在概率，即所有屬性存在概率累乘。式(1)可解決在不確定連續QoS屬性下Web服務存在概率的計算。

多數情況下，用戶喜歡通過計算QoS整體分值的方法找出滿足他們要求的Web服務。因此，本文定義了score(sj;q1,…,qn)來描述QoS的整體分值，記為score(sj)。QoS值是由聚合函數得到的，假設聚合函數是線性函數，QoS的權重已經被分配(默認的或者用戶定義)。這樣，score(sj)計算如下：

(2)

式(2)是一個聚合函數，通過聚合函數，將多個屬性聚合按照一定規則聚合成一個QoS值，用這種化多為少的方法可解決多目標決策問題。同時，計算中融入用戶需求和偏好計算的QoS值，更能準確地選擇滿足用戶需求的服務。

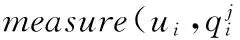
在文獻[4]中，為了計算的簡化，認為sj的存在概率為1，即sj的存在和它的屬性存在不相關；而另一種情況， 假定sj的存在概率是QoS值的存在概率。對于由連續不確定QoS屬性值計算得到的QoS值來說，每個記錄的QoS值也是連續不確定的，把它作為服務的一個特殊屬性值。此時，pr(sj)用pr(score(sj))表示。

在Web服務的中，以上兩種情況都有可能發生。所以，本文定義這兩種情況下的查詢語義。

例1假設表1中的QoS屬性的線性聚合函數為score(sj)=0.3·mprice+0.4·mw_l+0.3·mreputation。用戶想根據QoS值排名得到前二個的服務。由于 “sg.Court” 暫無房源，針對不同的查詢語義將得到不同的結果。例如，如果考慮所有服務都存在，返回的結果為{s1,s3}，而只考慮有房源的服務，則返回的結果為{s1,s2}。

針對第一種情況，以QoS記錄的存在概率為1為前提，這樣，返回結果排名只取決于QoS值的分布。本文對其做如下定義：

定義1Top-uncertain QoS:S={sj}是一組服務集，T={T1,…,Tm}， 是一組長度為k的服務向量集，每個Ti集中的服務都是根據QoS值進行排序。Top-uncertain QoS的返回結果記為T*，其中T*=argmaxT*∈T (∑sj∈T*pr(score(sj)))。

定義1和u-topk[5]相似，都是返回元組集中概率最大的K個服務。不同的是，u-topk所返回的是所有可能世界中發生概率最大的。而本文以服務的存在概率為1為前提，針對不確定的連續QoS屬性提出的一種查詢方法。

第二種情況，服務記錄是否存在由QoS值的存在概率決定。其中，QoS值的概率分布即是存在概率分布。在這種情況下，和Top-uncertain QoS的返回結果不同，因為對服務的排序不僅由QoS值也由它存在概率決定。例如，表1中有三個service，假設它們的存在概率不是1，由這三個服務組成的可能世界[5-7]有{s1},{s2},{s3},{s1,s2},{s2,s3},{s1,s3},{s1,s2,s3}。以服務s3為例，在不同的可能世界實例中，它的排序位置不同。

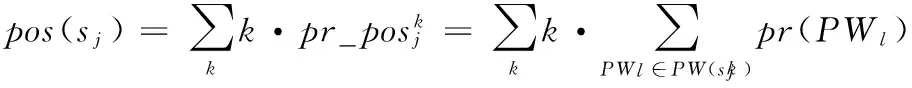
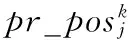
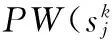
pr(PWl)是PWl的存在概率。它為其包含服務S的存在概率的累積。

此方法根據計算的位置函數值返回最優的K個服務。定義2類似于U-kRank[3,8,9]，都是通過計算可能世界中的位置排名返回最優的K個服務，不同之處定義2所計算的QoS值的概率作為記錄的存在的概率。

2查詢算法

對不確定數據進行排序和查詢選擇時需要考慮其概率和各屬性值之間組成的語義，文獻[5]提出了結合可信值和數據值的查詢算法U-topk和U-kRank。這兩種算法都是在數據概率離散情況下的處理方式，而對數據連續分布的情況未作出處理。本節提出的兩種查詢算法top-uncertain QoS和uncertain score rank，旨在解決不確定連續QoS的Web服務選擇。

不同的查詢語義所強調的是其所滿足的性質和應用環境。本文提出的兩種適用不同的應用環境的查詢語義算法。

2.1top-uncertain QoS計算

本方法中，假設QoS記錄存在概率為1。本文重點是通過QoS值的概率密度分布進行比較。QoS屬性值是不確定連續，而對于QoS值來說，每個記錄的QoS值也是連續不確定的，此時，服務的排序是由區間和概率密度分布決定的。當記錄相互獨立，QoS值具有相同概率密度分布時，通過比較積分面積[4]去比較哪個服務具有更高的服務質量的概率。具體如下：

首先，比較si和sj。si和sj的區間分別由[li,ui]和[lj,uj]表示。QoS值也有相同的概率分布。設概率密度函數為ρ。這樣得到：

假設sj也有相同的概率分布，當si和sj都是連續區間上的變量時，si的QoS值大于sj的概率為：

式中，ρi,j為si和sj的QoS值變量的聯合概率密度函數。Di,j表示u>v的積分域,即score(si)>score(sj)。

如圖1所示，x坐標和y坐標分別表示si和sj的區間。si和sj區間組成的面積被直線y=x分割成ai和aj兩個部分。如果ai>aj,則si的QoS值大于sj的QoS值可能性高，即pr(score(si)>score(sj))>pr(score(si)≤score(sj))。

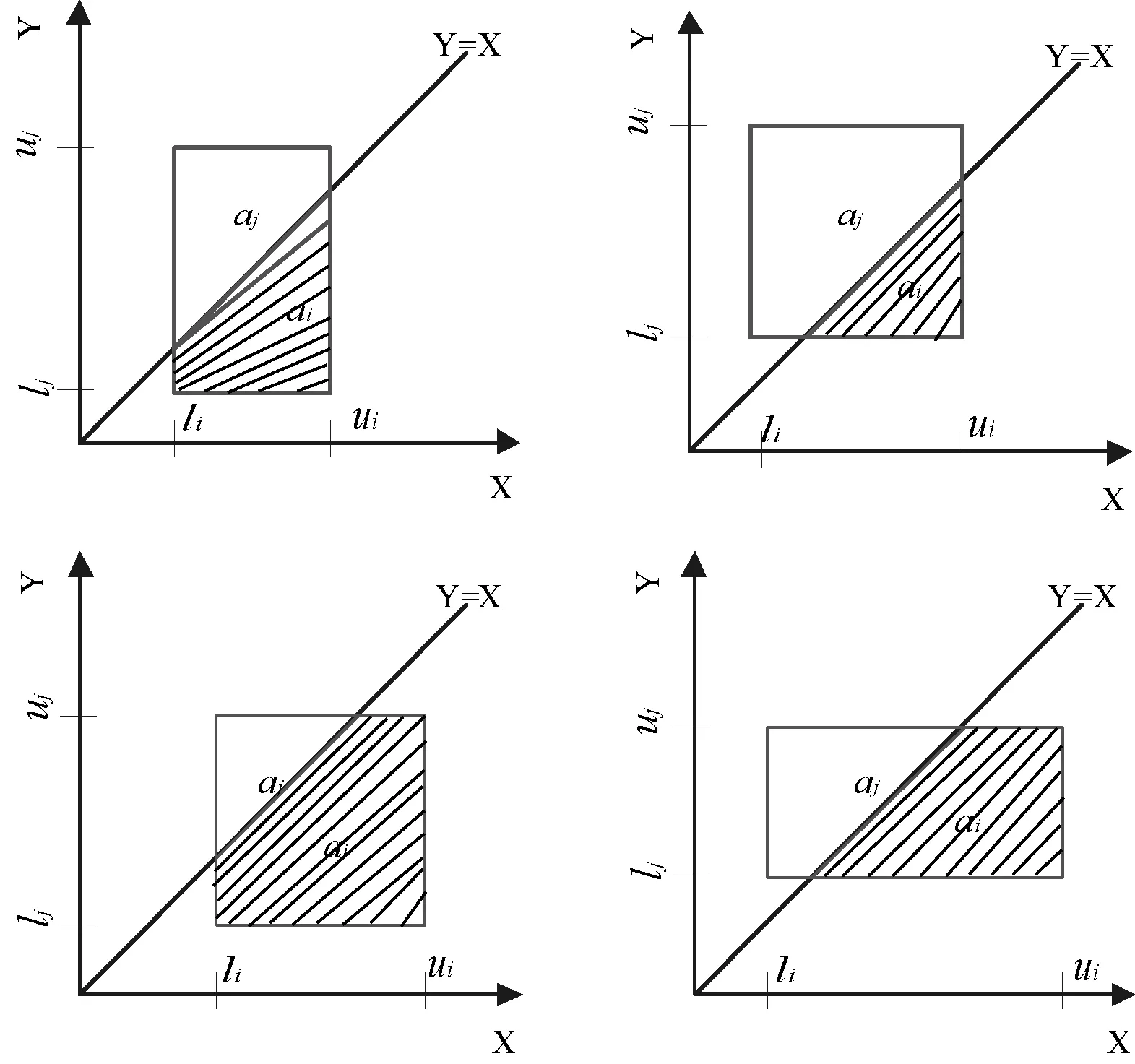
圖1　積分面積不同的情況

當記錄存在概率為1，QoS值符合相同密度分布時，top-uncertain QoS通過比較積分面積[4]計算兩服務之間具有更高的服務質量的概率，從而避免多重積分的計算，降低時間消耗。它不考慮記錄可信度，即假設記錄的存在概率為1。例如，在公寓查詢時，它沒有考慮無房源的情況。

下面是top-uncertain QoS的算法：

其中，comp(si,sj)表示比較哪個服務具有更高的服務質量，如果si>sj，則comp(si,sj)=1；否則為0。DS表示服務集；ret_serk代表服務返回的k個結果，當DS為空時算法終止。Queue存儲被訪問的、不在ret_serk里的服務集。

算法1top-uncertain QoS算法

1:初始化：Queue←φ，ret_ser0←φ

d←0表示查詢深度

2:ret_serk←DS中最先出棧k個

3:high,low←ret_serk中最大最小的代表值

4:while (DS≠φ) do

5:sd←DS中當前出棧的服務

6:if comp(high,sd)=0

7:if comp(sd,low)=1

8:ret_serk←sd

9:low←ret_serk中最小的代表值

10:else

11:Queue←sd

12:else

13:ret_serk←sd

14:high←sd

15:endif

16:endwhile

17:return ret_serk

2.2uncertain score rank計算

在計算top-uncertain QoS時，如果QoS記錄存在概率不等于1。根據該定義，需要掃描所有的可能世界。例如表1,3個服務產生7個可能世界。通常情況下，n個服務將產生2n個可能世界。由此可見，隨著服務數量的增加，可能世界會成指數級增加，這樣大大增加了計算的時間復雜度。

文獻[3]提出了一種剪枝的算法以減少運算代價。這種PRF方法基于離散不確定數據，當QoS值是離散的時候，遞減排序。對于服務si，{sj}i集表示QoS值高于si的集合。由于低于si的QoS值的服務不會對si的排名結果造成影響，所以{sj}i只考慮QoS值高于si的集合。文獻[8,9]提出了多項式系數的方法求解si排名k的所有可能世界的概率累和。其多項式公式如下：

(3)

將多項式展開如下：

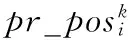
式(3)只考慮離散的不確定數據條件下，本文將它擴展應用到不確定的連續數據，uncertain score rank是利用PRF多項式系數得到服務排名位置的概率。然后計算返回pos(si)值最好的前K個。

綜上，當pr(sj)為pr(score(sj))時式(3)轉換為：

pr(score(sj)>score(si))x)

(1-pr(score(sj)≤score(si))x)

(4)

用變量v替換score(si)式(4)變為如下：

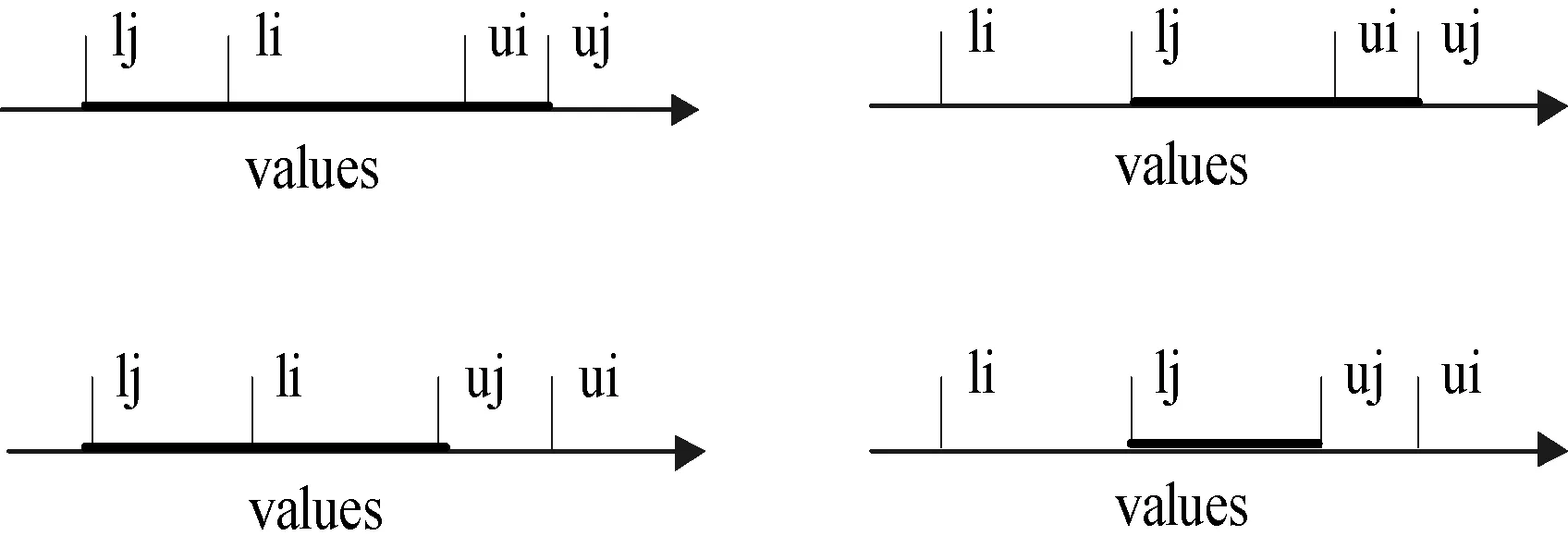
pr(score(sj)

整理得：

(5)

其中，ρi,j(u,v)是si和sj的QoS值的聯合概率密度函數。

得出：

化簡得：

(6)

其中，n是服務的總數。

用式(6)，可計算每個服務的pos(si)。最后返回pos值高的前k個。

Uncertain score rank算法考慮了記錄可信度。假定記錄的存在概率為QoS值的存在概率，對于由連續不確定QoS屬性計算得到的QoS值來說，每個記錄的QoS值也是連續不確定的，這種算法適用于對可信度要求較高的服務選擇情況。例如，在公寓查詢時，將無房源的情況考慮進去。

3實驗結果分析

目前互聯網的Web服務數量不超過10 000個，功能相同的服務也不超過300個，因此我們選擇Web服務數量的范圍在50到500之間。為驗證uncertain score rank和 top-uncertain ranking of QoS這兩種算法的可行性。本文模擬一個數據集，每個數據集有500條數據。每條記錄的上下界在[0,10]中間浮動，記錄的區間大小從0到10不等。本文假設概率分布分別符合均勻分布、標準正態分布和自定義正態分布的三種情況出發分析兩種方法的執行時間。

在Web服務中，受到開放性網絡的影響，其服務的響應時間集中在一定范圍內浮動，離散的數據未能正確反映原有數據的分布。同時如按照離散型QoS屬性值處理，當樣本數據量龐大，很難準確計算每條記錄的概率，如用簡單的概率分布函數表示存在概率，可避免每條記錄的概率計算。通過本實驗分析表明，該方法能有效解決Web服務QoS屬性連續條件下的查詢，具備一定的可行性。

3.1基于均勻分布和正態分布的uncertain score rank

利用式(6)，通過計算每個sj的prj,i來計算si的位置QoS值，si和sj無論屬于哪種概率分布。當ui

圖2　服務QoS屬性值區間

根據上述的4中情況，prj,i的計算如下：

(7)

根據式(6)、式(7)，可計算服務的位置QoS值。

在服務數量不同，返回服務個數不同的情況下，圖3分別表示均勻分布和正態分布條件下uncertain score rank的運行時間。

圖3　uncertain score rank運行時間

在正態分布的情況下，si的概率密度函數為：

圖3(b)和圖3(c)分別是標準正態分布和μ=7,σ=4的正態分布圖。運行時間隨著服務數量的增加而增加，而k值的變化對運行時間的影響并不大。

從圖3得出，對于不同的分布，時間消耗主要在可能性pr的計算上。

3.2基于均勻分布和正態分布的Top-uncertain ranking of QoS

這種方法，我們不需要計算位置的多重積分值，只需要比較服務si和sj的QoS屬性值區間所圍成的面積大小。而且不需知道其服務屬于哪種分布，即不同分布對此方法的時間消耗沒有影響。

圖4是不同的服務數量在兩種不同分布下的運行時間。

圖4　Top-uncertain ranking of QoS運行時間

4相關工作

隨著功能相似的Web服務的逐漸增多，基于QoS的Web服務選擇已經成為目前的一個研究熱點。

文獻[8]提出了一種可擴展的QoS計算模型，它是根據用戶反饋信息建立QoS信息的計算模型。文獻[9,10]提出了利用線性規劃的方法找到最佳服務。類似于這個方法，文獻[11]提出了帶有本地約束的線性編程模型。文獻[12]研究了在多個QoS約束條件下的服務選擇問題,它提出了兩種QoS組合中的融入啟發式算法的模型：(1) 組合模型；(2) 圖模型。文獻[13]介紹了一種用于評估多維屬性的QoS的選擇算法。以上的這些方法都是基于確定的QoS。

目前，也有不少針對不確定的QoS研究，文獻[1]介紹了離散的不確定QoS屬性，提出了一種對不確定QoS的描述方法，并給每個QoS屬性設立一個權值，計算出Web服務中每條記錄的加權QoS值之和進行排序。利用U檢驗或者峰度和偏態返回數值較小的Web服務。文獻[2,14-17]提出了Skyline的QoS查詢方法，這種方法不需要用戶給出QoS的權重。文獻[2,17]將Skyline的查詢方法應用到了不確定QoS中，并提出了一種提高Skyline查詢的效率方法。然而這些方法都是基于離散的不確定QoS。

連續的不確定性在文獻[3,4]中被提出來，它比離散的不確定性更加復雜。對于連續的不確定數據的查詢方法主要難點還是在查詢語義的定義[4]和不確定數據的表示[3]。

針對不確定數據查詢有不同的查詢語義[5]，這些方法都是基于離散的數據。本文在現有的基礎上，提出了基于連續不確定QoS的Web服務查詢方法。最后通過實驗驗證了本文方法的可行性。

5結語

本文根據不同的查詢語義，提出針對不確定的連續QoS屬性的查詢方法，并提出了QoS屬性值在一定分布下的優化方法。實驗表明，該方法能有效解決Web服務QoS屬性連續條件下的查詢，具備一定的可行性。接下去的工作主要集中以下兩點：(1) 討論涵蓋更多應用場景的查詢語義和研究相應的算法；(2) 研究如何優化技術，降低算法的復雜性，減少時間消耗。

參考文獻

[1] Cheng Wan,Hongbing Wang.Uncertainty-aware QoS Description and Selection Model for Web Services[C]//IEEE International Conference on Services Computing,Salt Lake City,UT:IEEE,2007.

[2] Karim Benouare,Djamal Benslimane,Allel Hadjali.Selecting Skyline Web Services from Uncertain QoS[C]//IEEE International Conference on Services Computing, HI:IEEE,2012.

[3] Jian Li,Amol Deshpande.Ranking Continuous Probabilistic Datasets[J].Proceedings of the VLDB Endowment,2010,3(1):638-649.

[4] Chonghai Wang,Liyan Yuan,Jiahuai You.On the semantics of top-k ranking for objects with uncertain data[J].Computers and Mathematics with Applications,2011,62(7):2812-2823.

[5] Soliman M,Ilyas I,Chang K C.Top-k query processing in uncertain databases[C]//IEEE 23rdInternational Conference on Data Engineering,Istanbul:IEEE,2007.

[6] Chonghai Wang,Li Yan Yuan,Jia Huai You,et al.On Pruning for Top K Ranking in Uncertain Databases[J].PVLDB,2011,4(10):598-609.

[7] Gupta R,Sarawagi S.Creating Probabilistic Databases from Informaiton Extraction Model[C]//Proceedings of the 32nd international conference on Very large data bases,2006.

[8] Jian Li,Barna Saha,Amol Deshpande.A Unified Approach to Raning in Probabilistic Databases[J].The VLDB Journal,2009,20(2):249-275.

[9] Jian Li,Amol Deshpande.Consensus answers for queries over probabilistic databases[C]//Proceedings of the twenty-eighth ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems,New York:ACM,2009.

[10] Liu Y,Ngu A H H,Zeng L.Qos computation and policing in dynamic web service selection[C]//Proceedings of the 13th international World Wide Web conference on Alternate track papers & posters,New York:ACM,2004.

[11] Zeng L,Benatallah B,Dumas M,et al.Quality driven web services composition[C]//Quality driven web services composition,New York:ACM,2003.

[12] Zeng L,Benatallah B,Ngu A H H,et al.Qos-aware middleware for web services composition[J].IEEE Trans. Software Eng,2004,30(5):311-327.

[13] Ardagna D,Pernici B.Adaptive service composition in flexible processes[J].IEEE Trans.Software Eng,2007,33(6):369-384.

[14] Yu T,Zhang Y,Lin K J.Efficient algorithms for web services selection with end-to-end qos constraints[J].ACM Transactions on the Web (TWEB),2007,1(1):1-26.

[15] Wang X,Vitvar T,Kerrigan M,et al.A qos-aware selection model for semantic web services[C]//Proceedings of the 4th international conference on Service-Oriented Computing,Berlin,Springer-Verlag,2006.

[16] Alrifai M,Skoutas D,Risse T.Selecting skyline services for qos-based web service composition[C]//Proceedings of the 19th international conference on World wide web,New York:ACM,2010.

[17] Yu Q,Bouguettaya A.Computing service skylines over sets of services[C]//2010 IEEE International Conference on Web Services,Miami,FL:IEEE,2010.

[18] Benouaret K,Benslimane B,HadjAli A.On the use of fuzzy dominance for computing service skyline based on qos[C]//2010 IEEE International Conference on Web Services, Washington,DC:IEEE,2011.

[19] Yu Q,Bouguettaya A.Computing service skyline from uncertain qows[J].IEEE T. Services Computing,2010,3(1):16-29.

收稿日期：2014-12-28。上海市自然科學基金項目(12ZR14110 00)；2015年度上海大學電影高峰學科成果。沈夢婷，碩士生，主研領域：Web service。劉方方，副教授。

中圖分類號TP3

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.07.006

UNCERTAIN QOS-BASED WEB SERVICES SELECTION

Shen MengtingLiu Fangfang

(SchoolofComputerEngineeringandScience,ShanghaiUniversity,Shanghai200444,China)

AbstractQuality of service (QoS) is considered as a significant criterion for Web services selection. Most of researches in regard to QoS-based Web services selection focus on the determined QoS data, such kind of means are not suitable for processing uncertain QoS attributes. However existing research means for uncertain QoS attributes are based on discrete QoS attributes and cannot deal with the situation when the QoS attributes are in continuity. Therefore in this paper, we present the query method for continuous QoS attributes with uncertainty, and propose the optimisation approach for QoS attributes under certain distribution. It is indicated by experiment that the method is able to effectively solve the query of Web services under the condition of QoS attributes in continuity, and it possesses certain feasibility as well.

KeywordsWeb serviceUncertaintyQoS