基于端元子集優選的高光譜解混算法研究

劉萬軍　楊秀紅　曲海成,2　孟　煜　姜慶玲

1(遼寧工程技術大學軟件學院　遼寧 葫蘆島 125105)2(哈爾濱工業大學電子與信息工程學院　黑龍江 哈爾濱 150006)3(鐵嶺師范高等專科學校　遼寧 鐵嶺 112000)

?

基于端元子集優選的高光譜解混算法研究

劉萬軍1楊秀紅1曲海成1,2孟煜1姜慶玲3

1(遼寧工程技術大學軟件學院遼寧 葫蘆島 125105)2(哈爾濱工業大學電子與信息工程學院黑龍江 哈爾濱 150006)3(鐵嶺師范高等專科學校遼寧 鐵嶺 112000)

摘要針對采用最大體積單體MVS(Maximization Volume Simplex)端元提取算法進行端元初選時存在相似端元光譜問題，提出一種光譜信息散度SID(Spectral Information Divergence)和光譜梯度角SGA(Spectral Gradient Angle)相結合以區分兩個相似端元光譜的方法。該方法對經過端元初選之后的端元子集進行端元的二次選擇，采用以SID_SG作為最相似端元選擇的判據，除去相似端元，降低相似端元對解混精度的影響，利用全約束最小二乘法進行豐度估計。實驗結果表明，提出的優化方法與傳統方法相比，提高了端元的選擇精度，重構影像與原始影像之間的均方根誤差RMSE(Root Mean Square Error)也有所降低，分布更加均勻。該方法對高光譜遙感影像進行深度解譯具有十分重要的意義。

關鍵詞光譜解混端元初選二次提取除去端元解混算法

0引言

高光譜遙感技術已經廣泛應用于軍事和民用等各個領域。然而，阻礙高光譜遙感技術向定量化方向深入發展的主要因素是混合像元的普遍存在[1]。因為高光譜傳感器有限的空間分辨率，每個像元對應著較大的區域，所以每個像元一般包含多種物質，多種物質光譜混合的混合光譜就是傳感器探測的光譜[2]。解決混合像元問題最有效的方法就是混合像元分解[3]。高光譜混合像元分解一般包括兩個方面，分別是端元提取[4]和豐度估計[5]。當前端元提取方法有N-FINDR[6]、頂點成分分析[7]VCA(Vertex Component Analysis)、迭代誤差分析IEA(Iterative Error Analysis)[8]和純像元指數PPI(Pure Pixel Index)等。傳統的豐度估計算法主要有非限制性最小二乘法，非負限制性最小二乘法，和為一限制性最小二乘法和全限制性最小二乘法[9]。在進行高光譜解混時需要盡可能地選擇出最精確的端元，降低解混時出現的誤差。

本文結合兩種常用的光譜區分方法，提出了一種將光譜信息散度和光譜梯度角相結合的方法用以區分兩個相似端元光譜。該方法不僅能夠從形狀上反映兩條光譜曲線的匹配程度，而且能夠對兩條有較小差異的光譜曲線做出較大的響應。首先利用最大體積單體端元提取算法進行端元的初次提取，然后再利用光譜信息散度和光譜梯度角SID_SG(Spectral Information Divergence_ Spectral Gradient)相結合的算法找出端元子集中存在的相似端元，去除相似端元，最后利用全約束最小二乘法FCLS(Full Constraint Least Square)進行端元的豐度估計，從而實現高光譜的混合像元分解。

1高光譜解混算法

1.1最大體積單體MVS

一般而言，高光譜圖像中的每個像元都能看作是圖像中各端元的線性混合的像元:

(1)

(2)

0≤ki≤1

(3)

式中，x是高光譜圖像中任一P維的光譜向量(P為圖像的波段數目)，E=[e1,e2,…,en]是P×N的矩陣，N是端元的數目，E中的每一列都是端元向量。c=(c1,c2,…,cn)T是系數向量，ci是像元x中端元ei所占比例，n表示誤差項。

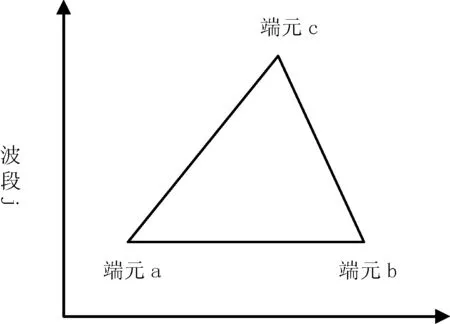
圖1　兩個波段三個端元

在誤差項n非常小時，只有滿足上面3個式子的點的集合，才能夠構成高維空間的凸集，這些端元就坐落在凸面的單形體的各個頂點[10]。這里采用兩個波段、三個端元作為例子，從而清晰地表明它們之間存在的幾何關系，如圖1所示。從圖1中看出,三角形體的各個頂點分別是端元a、b和c，那么三角形內部的點就對應著圖像中混合像元。所以提取高光譜圖像的端元問題就轉化成求單形體的頂點問題[11]。

從圖1可以看出，圖1中的端元a，端元b以及端元c所構成的三角形面積是圖像中的任意三個像元所構成的面積集合中的最大的一個，表示如下:

S(a,b,c)=max{S(i,j,k)}

(4)

式中，S(i,j,k)表示的是由像元i、j和k所構成的三角形面積。所以尋找單形體的頂點的問題就轉化為求最大體積單體的問題，體積公式如下:

(5)

(6)

式中，ei表示第i個端元的列向量，V表示的是由e1,e2,…,en這N個端元所構成的單形體體積，|·|表示行列式的運算符。因為這里用到了求行列式的運算，所以要求E必須為方陣。

1.2光譜信息散度SID

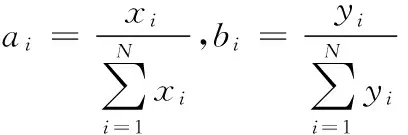
Ii(x)=-lgai

(7)

Ii(y)=-lgbi

(8)

通過式(7)和式(8)，可得y關于x的相對熵：

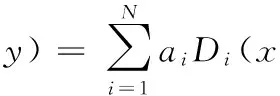
(9)

同樣可以得到x關于y的相對熵：

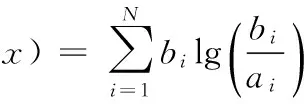
(10)

因而x和y的光譜信息散度為：

SID(x，y)=D(x‖y)+D(y‖x)

(11)

光譜信息散度法的優點是可以對兩條光譜進行整體上的比較。

1.3光譜梯度角SGA

光譜梯度角是在對兩條光譜向量一階求導的基礎上求解它們的梯度向量，然后再得出兩個梯度向量間的廣義夾角大小[13]。

光譜曲線x的梯度向量為：

sGA(x)=[x2-x1,x3-x2,…,xn-xn-1]

(12)

光譜曲線y的梯度向量為：

sGA(y)=[y2-y1,y3-y2,…,yn-yn-1]

(13)

則梯度向量的廣義夾角大小為：

(14)

該方法的優勢在于能夠反映光譜曲線的斜率變化，能反映出光譜曲線的局部特征的變化。

1.4信息散度與梯度角相結合

兩條光譜曲線的銳角夾角范圍是(0,π/2)，并且梯度向量的銳角夾角范圍同樣是(0,π/2)。因為正切函數的特性是當夾角是π/4時值為1；當夾角大于π/4時，其值隨著夾角的增大迅速變大。根據正切的函數特征，將光譜梯度夾角控制在[π/4，π/2]范圍內，當夾角值改變較小時，其結果就能有明顯變化。因此為了不僅可以在整體上比較兩條光譜曲線的匹配程度，而且可以從局部上區分兩條光譜曲線的差異，提出將SID與SGA相結合的公式如下：

(15)

1.5均方根誤差RMSE

RMSE[14]是均方根誤差，是一個度量準則，用來評價兩幅圖像的相似性，均方根誤差越小，說明二者越相近。

(16)

式中，假設端元豐度矩陣為S=(s11,s12,…,s1n;…;sp1,sp2,…,spn),真實豐度矩陣為Z=(z11,z12,…,z1n;…;zp1,zp2,…,zpn),sij和zij分別為矩陣S和Z的第i行第j列元素。

1.6豐度估計誤差

(17)

式中，m是圖像中混合光譜條數；n是端元組中端元個數；qij是第i條光譜第j個端元的計算豐度值；pij是第i條光譜第j個端元的假定豐度值；fa是豐度估計誤差。

2基于端元子集優選的高光譜解混

利用最大體積單體端元提取算法進行端元的初次提取，先去除部分端元，再進行端元的二次提取迭代循環，去掉相似的端元，剩下的端元為最佳端元，最后再利用全約束最小二乘法進行豐度的估計，最終實現高光譜的混合像元分解。端元初次提取的目的是為了去除部分多余的端元，端元二次選擇的目的是進一步從原始高光譜影像中找到純像元，從而準確求解各純物質在混合像元中所占的比例。以SID_SG作為最相似的端元選擇準則，能夠選擇出最相似的端元組，去除均方根誤差較大的端元，保留均方根誤差較小的端元，從而降低相似端元對解混精度的影響。

算法流程如圖2所示。

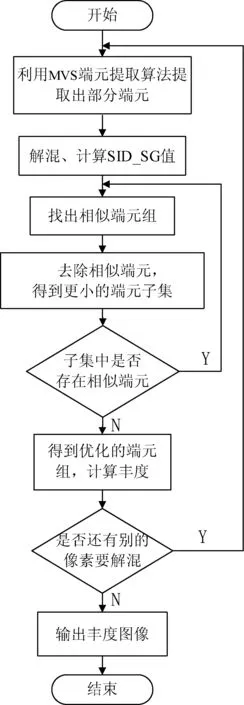
圖2　基于端元子集優選的高光譜解混算法流程圖

端元二次選擇優選算法步驟：

步驟1找出一組相似端元。將端元集合利用光譜匹配算法SID_SG進行第一次循環，找出最相似的一組端元，分別是端元A和端元B。

步驟2計算出去除端元A后的均方根誤差。去除端元集合中的端元A，利用剩下的端元計算出均方根誤差。

步驟3計算出去除端元B后的均方根誤差。去除端元集合中的端元B，利用剩下的端元計算出均方根誤差。

步驟4比較步驟2和步驟3中的均方根誤差。將步驟2和步驟3中計算出的均方根誤差進行對比，留下均方根誤差比較小的端元。

步驟5重復步驟1～4，直至選出均方根誤差最小并且求解豐度所運行的時間是最小的端元組，最終形成新的端元集合。

選出優化后的端元組之后，再采用全約束最小二乘法求解高光譜最終的豐度。

3實驗結果分析

3.1端元數目不同時的對比實驗

該實驗采用的模擬圖像大小是64×64，端元數目是3至8個，并且添加的信噪比SNR(Signal to Noise Ratio)為30 dB。在端元數目不同的情況下對比N-FINDR、單體增長算法SGA(Simplex Growing Algorithm)和最大體積單體(MVS)這三種端元提取算法的優劣，見表1所示。

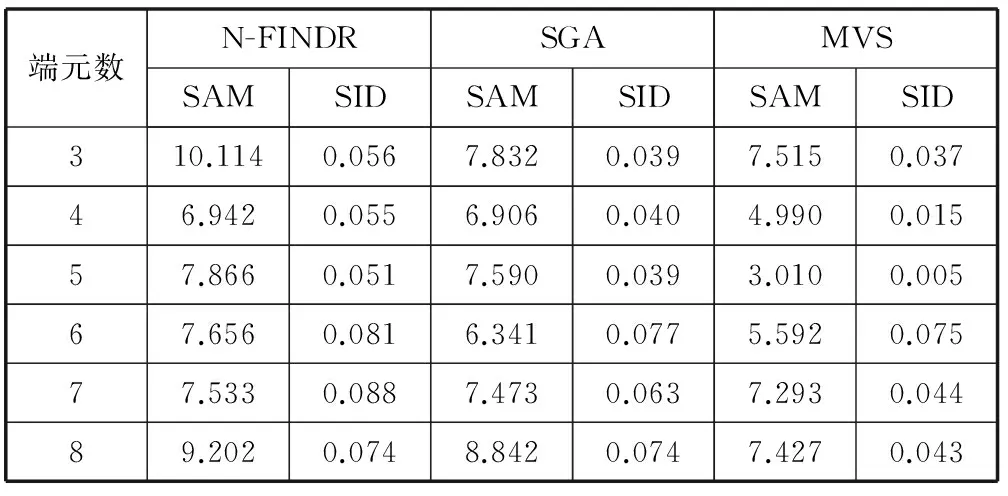
表1　端元數不同時的實驗對比

從表1中可以看出，N-FINDR、單體增長算法(SGA)、最大體積單體(MVS)這三種算法在端元數目不同的情況下對端元提取的結果進行相似性度量的對比。隨著端元數目的增多， MVS算法的效果是最好的，SGA算法要優于N-FINDR算法，所以采用MVS算法進行端元初次選擇的效果要優于SGA算法和N-FINDR算法。

3.2信噪比不同時的對比實驗

該實驗采用的模擬圖像是64×64，端元數目是4條，并且添加的信噪比為10至50 dB。在不同的信噪比下對比N-FINDR，單體增長算法(SGA)，最大體積單體(MVS)這三種端元提取算法的魯棒性，見表2所示。

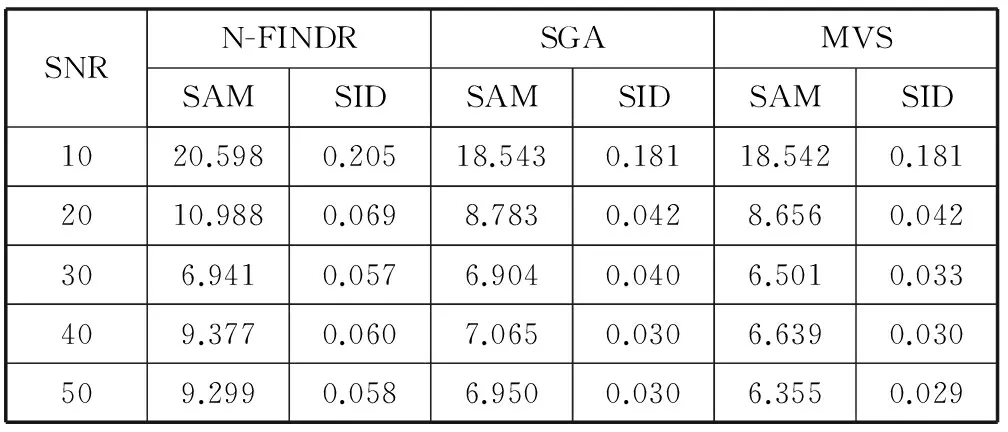
表2　信噪比不同時的實驗對比

從表2中可以看出，N-FINDR、單體增長算法(SGA)、最大體積單體(MVS)這三種算法在信噪比不同的情況下對端元提取的結果進行相似性度量的對比。對比表2中數據發現N-FINDR、SGA和MVS這三種算法的魯棒性從高到低依次是MVS算法、SGA算法、N-FINDR算法，所以采用MVS算法進行端元的初次選擇的穩定性要優于SGA算法和N-FINDR算法。

3.3分類精度對比實驗

實驗數據集為高光譜研究中經常采用的Pavia數據[15]，該研究區域位于意大利北部的帕維亞，該地區地形復雜，主要有灌木、水體、森林、農田、草地和城鎮等地物類型。

為了更好地證明SID_SG方法的優越性，利用實驗數據將SID_SG方法與光譜角匹配SAM(Spectral Angle Mapping)法，光譜信息散度(SID)法，光譜梯度角(SGA)法這三種方法做對比實驗，將它們在分類精度上進行對比驗證，見表3所示。

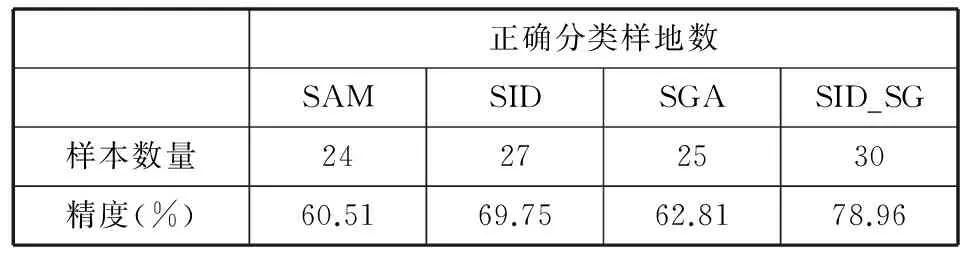
表3　不同分類方法的精度分析

從表3中可以看出，分類精度最高的是SID_SG，達到78.96%，它對所調查的樣本點正確分類的個數是30個。分類精度最低的是SAM，它的精度是60.51%，它對所調查的樣本點正確分類的個數是24個。SID的分類精度低于SID_SG的分類精度，高于SAM的分類精度，它對所調查的樣本點正確分類的個數是27個，其精度是69.75%。SGA的分類精度也低于SID_SG的分類精度，高于SAM的分類精度，它對所調查的樣本點正確分類的個數是25個，其精度是62.81%。從這些數據可以看出，SID_SG的分類精度要高于SAM、SGA和SID，所以采用SID_SG算法提取相似端元的效果要優于SAM、SGA和SID。

3.4均方根誤差及豐度估計時間對比

實驗數據集為高光譜解混研究中經常采用的美國 Nevada 州南部沙漠地區的Cuprite數據[16]。該數據中共有224個波段，波長范圍為0.37到2.48 μm，光譜分辨率是10 nm。

RMSE是均方根誤差，是一個度量準則，用來評價兩幅圖像的相似性，均方根誤差越小，說明二者越相近。

利用實驗數據，根據本文優選算法分別提取出不同的端元數，得到的RMSE隨著端元個數增加的變化情況，如圖3所示。利用全約束最小二乘法解混求豐度運行的時間，見表4所示。根據圖3中不同端元數目得出的均方根誤差值以及表4中給出的在不同端元數目下利用全約束最小二乘法解混求解豐度所運行的時間值可以看出去除十個相似的端元是最適宜的，所以在端元二次提取時提取出12個端元是最合適的。

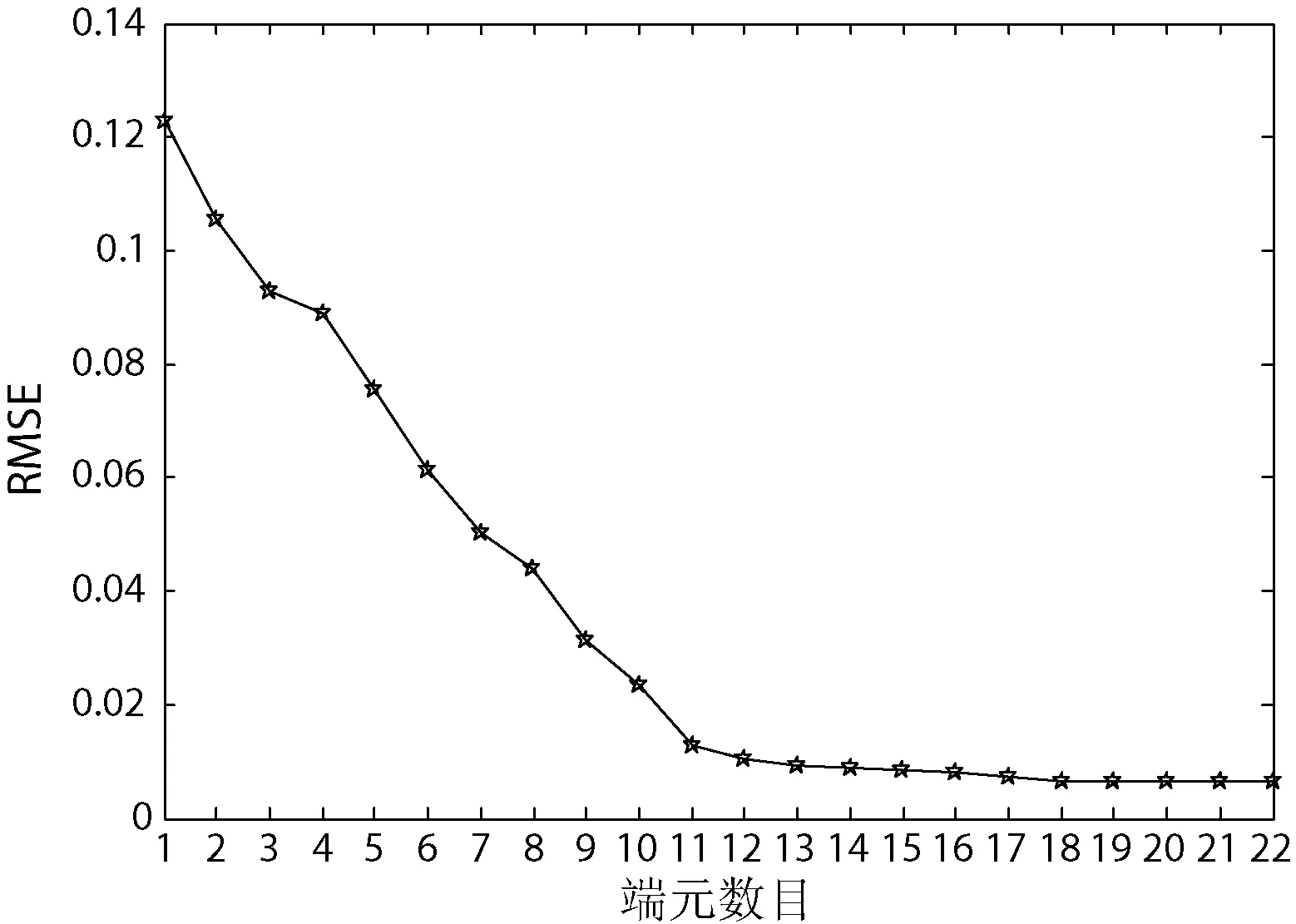
圖3　端元數目和RMSE值的關系

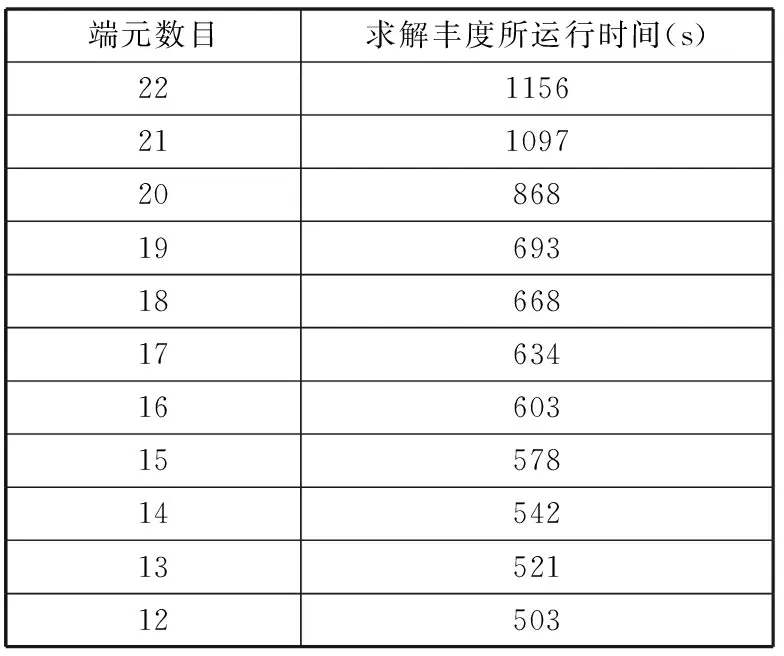
端元數目求解豐度所運行時間(s)221156211097208681969318668176341660315578145421352112503

3.5整體豐度估計誤差對比

為了研究噪聲對本文算法性能的影響, 本文在混合光譜中加入了隨機噪聲。加入噪聲的公式為：

(18)

式中，r′是加噪聲之后的光譜；r是無噪聲的光譜；u(0,1)是均值為0，方差為1的隨機噪聲；SNR是信噪比；X是噪聲的假想發射率，假定為0.5。

本文實驗中將本文算法、MVS算法以及FCLS算法進行對比，這三種算法的豐度估計誤差隨信噪比的變化情況，如圖4所示。

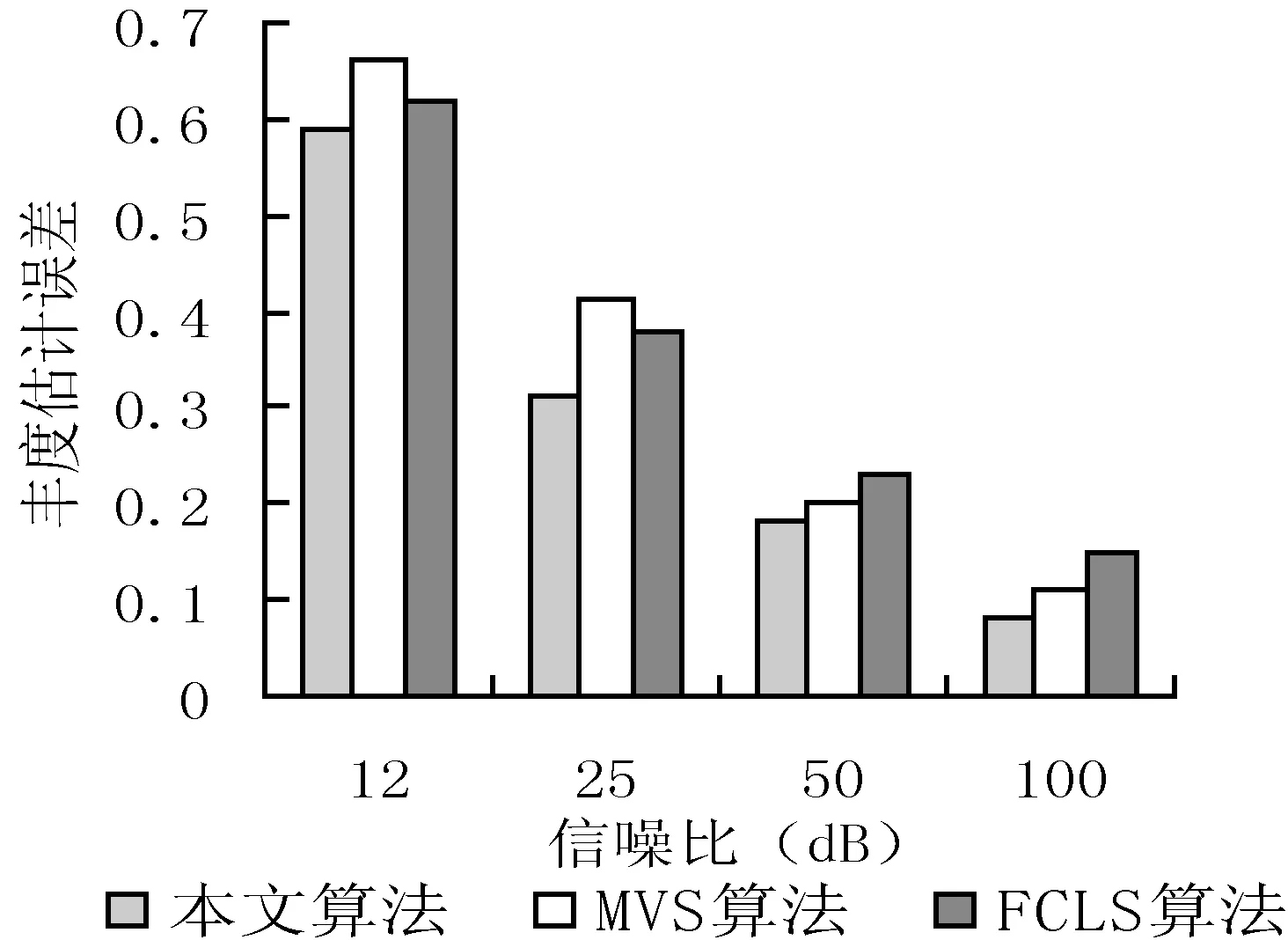
圖4　三種算法的豐度估計誤差隨信噪比變化情況

從圖4中可以看出, 當信噪比SNR的范圍是[12，100]時, 本文算法豐度估計誤差fa是最小的，并且當信噪比達到100時，本文算法的豐度估計誤差小于0.1，綜上所述，本文算法要優于最大體積單體算法和全約束最小二乘算法。

3.6優選前后端元及誤差分布對比

利用Cuprite數據進行優選前后的誤差分布圖對比。在端元初選時，利用最大體積單體端元提取算法進行端元的一次提取處理，提取出22個端元，得到其誤差分布圖，如圖5所示。對22個端元進行端元的二次提取處理后，得到12個端元的誤差分布圖，如圖6所示。

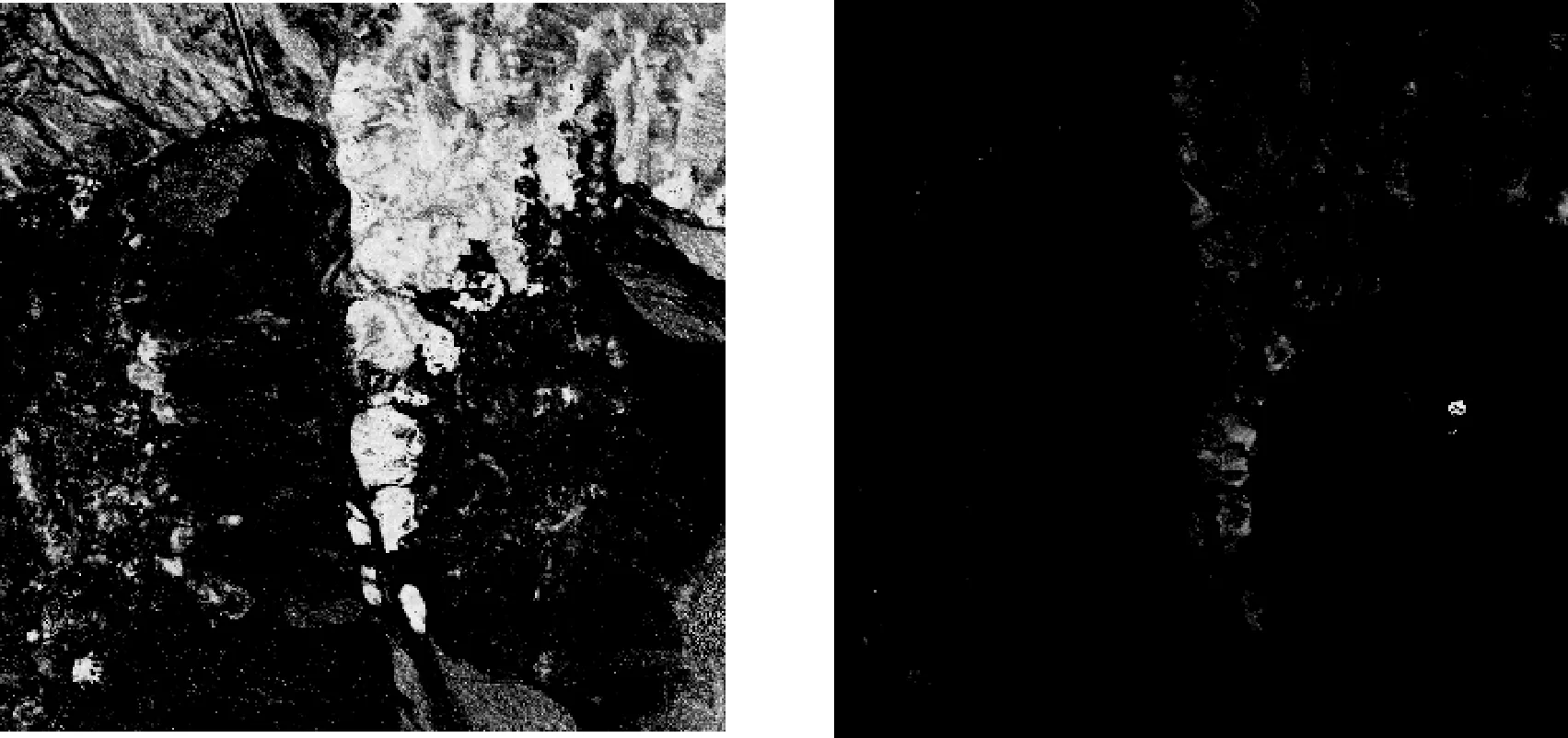
圖5　初次提取誤差分布圖　　圖6　二次提取誤差分布圖

對比圖5和圖6，可以看出優選后誤差分布更加均勻，降低了誤差，提高了端元選擇的精度，減少了相似端元對解混精度的影響。

4結語

本文提出了一種將光譜信息散度和光譜梯度角相結合的方法用以區分兩個相似端元光譜。在利用最大體積單體端元提取算法進行端元初選之后，再采用以SID_SG作為最相似端元選擇的判據進行端元的二次選擇，除去相似的端元，降低相似端元對解混精度的影響。從實驗的結果可以看出, 提出的基于端元子集優選的高光譜解混算法比傳統算法提高了端元的選擇精度，分布也更加均勻，同時也減少了重構影像與原始影像之間的均方根誤差(RMSE)。該方法對高光譜遙感影像進行深度解譯具有十分重要的意義。

參考文獻

[1] Chen G,Song F,Wang J,et al.FRET spectral unmixing:a ratiometric fluorescent nanoprobe for hypochlorite[J].Chemical Communications,2011,24(4):2949-2951.

[2] Roth K L,Dennison P E,Roberts D A.Comparing endmember selection techniques for accurate mapping of plant species and land cover using imaging spectrometer data[J].Remote Sensing of Environment,2012,32(8):139-152.

[3] Gu Y,Wang S,Jia X.Spectral unmixing in multiple-kernel hilbert space for hyperspectral imagery[J].Gon and Rmo Nng Ranaon on,2013,51(10):3968-3981.

[4] Martin G,Plaza A.Spatial-spectral preprocessing prior to endmember identification and unmixing of remotely sensed hyperspectral data[J].Ld O N Ald Arh Obrvaon and Rmo Nng Jornal of,2012,5(12):380-395.

[5] Gonzalez C,Resano J,Plaza A,et al.FPGA implementation of abundance estimation for spectral unmixing of hyperspectral data using the image space reconstruction algorithm[J].Ld O N Ald Arh Obrvaon and Rmo Nng Jornal of,2012,5(3):248-261.

[6] Xiong W,Chang C,Wu C,et al.Fast algorithms to implement N-FINDR for hyperspectral endmember extraction[J].Ld O N Ald Arh Obrvaon and Rmo Nng Jornal of,2011,4(3):545-564.

[7] Krafft C,Diderhoshan M A,Recknagel P,et al.Crisp and soft multivariate methods visualize individual cell nuclei in Raman images of liver tissue sections[J].Vibrational Spectroscopy,2011,55(1):90-100.

[8] Fang Y,Yan H.Error analysis for remote nonlinear iterative learning control system with wireless channel noise[J].Journal of Shanghai University (English Edition),2011,15(3):7-11.

[9] Chang C I.An information-theoretic approach to spectral variability,similarity,and discrimination for hyperspectral image analysis[J].IEEE Transactionson InformationTheory,2000,45(5):1927-1932.

[10] 耿修瑞,張兵,張霞,等.一種基于高維空間凸面單行體體積的高光譜圖像解混算法[J].自然科學進展,2004,7(14):810-814.

[11] 耿修瑞,趙永超,周冠華.一種利用單行體體積自動提取高光譜圖像端元的算法[J].自然科學進展,2006,9(16):1196-1200.

[12] Jarosik N,Bennett C L,Dunkley J,et al.Seven-year wilkinson microwave anisotropy probe (WMAP) observations: sky maps,systematic errors,and basic results[J].The Astrophysical Journal Supplement Series,2011,192(2):14.

[13] Liu J,Zhang J.A new maximum simplex volume method based on householder transformation for endmember extraction[J].Ranaon on Gon and Rmo Nng,2012,50(6):104-118.

[14] Chai T,Draxler R R.Root mean square error (RMSE) or mean absolute error (MAE)?[J].Geoscientific Model Development Discussions,2014,7(1):1525-1534.

[15] Brasco L,Pratelli A.Sharp stability of some spectral inequalities[J].Geometric and Functional Analysis,2012,22(1):107-135.

[16] Chen B,Vodacek A,Cahill N D.A novel adaptive scheme for evaluating spectral similarity in high-resolution urban scenes[J].Selected Topics in Applied Earth Observations and Remote Sensing,IEEE Journal of,2013,9(3):1376-1385.

收稿日期：2014-09-28。國家高技術研究發展計劃項目(2012AA 12A405)；國家自然科學基金項目(61172144)。劉萬軍，教授，主研領域：數字圖像處理，運動目標檢測與跟蹤。楊秀紅，碩士。曲海成，博士。孟煜，碩士。姜慶玲，博士。

中圖分類號TP75

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.07.058

HYPERSPECTRAL UNMIXING ALGORITHM BASED ON ENDMEMBER SUBSET OPTIMISATION

Liu Wanjun1Yang Xiuhong1Qu Haicheng1,2Meng Yu1Jiang Qingling3

1(SchoolofSoftware,LiaoningTechnicalUniversity,Huludao125105,Liaoning,China)2(SchoolofElectronicsandInformationEngineering,HarbinInstituteofTechnology,Harbin150006,Heilongjiang,China)3(TielingNormalCollege,Tieling112000,Liaoning,China)

AbstractFor the problem of maximisation volume simplex (MVS)endmember extraction algorithm that when applying in primary endmembers selection it would have similar endmembers spectra, we proposed an algorithm which distinguishes two similar endmember spectra by combining the spectral information divergence (SID) and the spectral gradient angle (SGA). This algorithm carries out secondary selection on the endmember subset derived from primary endmembesr selection, and adopts SID_SG rule as the criteria for selecting the most similar endmembers to remove the similar endmembers and to reduce the influence of similar endmembers on unmixing accuracy, and uses the full constraint least square for abundance estimation. Experimental results showed that proposed optimisation algorithm improved the accuracy of endmember selection than the traditional method, the root mean square error (RMSE) between reconstruction images and original image was rather reduced, and the distribution was more evenly as well. The algorithm is of very great significance to the deep interpretation on hyperspectral remote sensing image.

KeywordsSpectral unmixingPrimary endmembers selectionSecondary extractionRemoval of endmemberUnmixing algorithm