基于社交網絡節點中心度挖掘其社區框架

王童童　李盛恩　王　剛

(山東建筑大學計算機科學與技術學院　山東 濟南 250101)

?

基于社交網絡節點中心度挖掘其社區框架

王童童李盛恩王剛

(山東建筑大學計算機科學與技術學院山東 濟南 250101)

摘要社區結構作為真實復雜網絡所普遍具有的一個重要的拓撲特性，最近10年內得到了廣泛而深入的研究。為解決社區挖掘策略時間復雜度過高、缺少與用戶交互等問題，討論了社交網絡節點中心度、度的冪律分布等特性，提出了“關鍵子網絡”和“社區框架”的概念，設計了社區框架挖掘算法MCF(Mine the Community Framework)和社區框架鉆取算法DCF(Drill Down the Community Framework)，其中MCF算法用于挖掘社交網絡的社區框架，DCF用于對社區框架進行鉆取，從不同粒度展現社區結構。實驗結果和實驗分析表明，MCF算法能夠在較短時間內挖掘出反映復雜網絡社區狀態的社區框架，DCF算法可以以用戶交互方式實現高質量的社區劃分。

關鍵詞社交網絡社區結構節點中心度社區框架社區質量

0引言

真實世界中的許多復雜系統可以表示成圖或者網絡，包括社交網絡、信息網絡、生物網絡和技術網絡等[1]。經驗分析表明，這些復雜網絡往往是由若干個節點組構成，節點組內部的連接相對緊密，而節點組之間的連接卻相對比較稀疏。我們稱網絡的這種拓撲特性為社區結構，相應地，每個節點組被稱為一個社區。不同的應用領域，社區結構具有不同的內涵。比如，社交網絡中一個社區代表了具有相似特征的人群；生物網絡中的社區解釋了具有相似功能的生物組織模塊；Web網絡中的文檔類簇包含了大量的具有相關主題的Web文檔等[2]。社區挖掘就是對這些不同類型復雜網絡進行處理，挖掘出社區結構，從而來幫助人們理解復雜網絡的功能，發現復雜網絡中隱藏的規律和預測復雜網絡的行為[3]。

雖然現在發展出了大量的社區挖掘策略，例如GN算法[4]、譜分解算法[5]等，然而這些社區挖掘算法大部分都是直接針對完整社交網絡數據進行社區挖掘。例如GN需要反復計算整個網絡的任意兩點的最短路徑，譜分解算法需要將每一個節點在向量空間中加以表示。這樣的處理策略還存在不足之處：首先，使用社區挖掘策略對一個很大的社交網絡進行社區挖掘需要大量的計算，計算時間長，例如GN算法時間復雜度為O(n2m)，譜分解算法為O(n2)，其中n為節點個數，m為邊的條數；其次，即使挖掘出社區結構，這個社區結構將涉及所有點的信息，社區結構過于復雜；最后，這些社區挖掘策略在設置完初始參數后，就開始計算，然后返回給用戶整個網絡的社區劃分，計算過程中，用戶不能進行控制，缺乏交互。

文獻[6,7]指出在社交網絡中存在少部分的節點中心度較高的節點，其構成的子網絡能夠反映整個社交網絡的拓撲特性。為了能夠快速對社交網絡進行社區挖掘，并且讓用戶能夠控制挖掘的粒度，受其啟發我們提出了關鍵子網絡的概念，進而提出了MCF算法和DCF算法。MCF算法利用社交網絡的節點中心度提取出社交網絡的關鍵子網絡，關鍵子網絡的結點數和邊數遠小于原社交網絡，同時保持了原社交網絡的拓撲特性。然后利用經典的挖掘算法對關鍵子網絡進行社區挖掘，將獲得的社區框架作為整個社交網絡的社區概況，這樣可以在很大程度上減少計算量，縮短計算時間。用戶如果想獲得社區結構的更詳細信息，可使用DCF算法對社區框架添加一些節點。然后再進行計算，這樣在用戶的控制下，逐步得到整個社交網絡的社區劃分，這種挖掘方式類似于在商務智能領域獲得成功的OLAP中的下鉆操作。

1社交網絡與社區結構

社交網用無向圖G(V,E)來表示，其中V表示參與社交網絡的參與者，E表示參與者之間的關系。對于一個無向圖，在計算機中我們可以使用鄰接矩陣來表示：

(1)

從鄰接矩陣A可知，如果節點i和節點j之間存在聯系，則Aij與Aji都為1，否則都為0，所以鄰接矩陣A是一個對稱矩陣。若求得了一個社交網絡的鄰接矩陣A，就能夠很容易計算出每個節點的度：設定 1n是一個n維并且每一個元素都為1的列向量，則度向量K=A·1n指明了每一個節點的度，其中Ki為節點i的度。

隨著對各種網絡的深入研究，發現許多實際網絡都存在社區結構，Newman等人給出了社交網絡社區結構的定義：社區是社交網絡中的子網絡，子網絡內部聯系緊密，子網絡之間聯系稀疏[8]。如圖1的社交網絡體現了①②③三個社區，通過觀察能夠發現，在社區內部邊的密度要大于社區之間邊密度。

圖1　社區結構示意圖[8]

社交網絡的一個社區，往往反映了在這個社交網絡中，具有共同興趣愛好，或者其他共同特性的一群個體。通過研究社交網絡的社區結構我們能夠了解社交網絡的深層結構，及其內部錯綜復雜的關系。為此發展出了很多的社區結構發現策略，基于其原理可分為基于劃分的、基于模塊性優化、基于標簽傳播、基于動力學和基于仿生計算的方法等[9]。

然而對于同一個社交網絡我們應用不同的社區劃分方法會得到不同的社區劃分，即使使用相同的社區挖掘策略有時也會得到不同的社區劃分，為了衡量對一個網絡社區劃分的好壞，基于社區內部聯系緊密社區之間聯系稀疏的思想，Newman和Girvan提出了著名的模塊度函數即Q函數[10]。其定義為：

假定社交網絡被某種挖掘策略分解成n個社區，定義一個n×n的對稱矩陣E=(eij)。其中eij表示社交網絡中位于社區i和社區j之間的邊數占總邊數的比例；E中對角線上的元素之和稱為該矩陣的跡，即：Tre=∑ieii，它表示社交網絡中位于社區內部的邊數占總邊數的比例；定義矩陣E中每行或者每列中各個元素之和為ai=∑eij，它所表示社交網絡中與第i個社區中節點相連的邊在所有邊中所占的比例。在此基礎上定義網絡劃分的模塊度為：

式中‖e2‖表示矩陣e2中所有元素之和。Tre表示網絡中位于社區內部邊數所占圖中總邊數的比例，‖e2‖表示社區內部邊數所占總邊數比例的期望。如果社區內部邊數的比例不大于任意連接時的期望值則Q=0。Q的最大值為1，Q越接近1，則說明網絡的社區劃分的質量越好，即社區內部聯系越緊密。在實際網絡中該值通常位于0.3到0.7之間。

模塊度函數表示在節點上的式子為：

(2)

其中P為社區挖掘算法所發現的社區的集合，m為社交網絡中邊的條數。若節點i和j其度分別為ki與kj，則(ki×kj)/2m計算了兩節點之間有邊的概率，因此公式中減數部分計算了社區內部邊的條數的期望。

2社區框架的挖掘及鉆取

現實世界中，我們發現每一個社區中都有很多在該社區中具有重要地位的焦點人物，他們管理組織社區并經常與其他社區的參與者互動。通過對這些重要參與者的社區考察，我們能夠總結出整個網絡的社區狀態。例如在合著網絡中，每一個領域都有很多頂尖學者，可以將這些學者提取出來構成一個網絡來對其進行社區劃分，用以反映整個網絡的社區狀態。我們提取的由重要參與者構成的網絡叫做原社交網絡的關鍵子網絡，其社區劃分稱之為社區框架。當想獲得更多社區細節時，我們可以向社區框架中添加節點進行鉆取。

2.1節點中心度

中心度就是用來評價一個社交網絡中節點重要性的概念。它是關于參與者在社交網絡中的中心型位置的測量概念，反映的是不同參與者在社交網絡中位置或者優勢的差異[6]。現在已經存在很多對社交網絡中心度進行測量的方法，有些側重于局部的參與者，如局部點中心度；有些側重整體網絡結構，如總體中心度。局部點中心度簡稱為點中心度，其所反映的是某個節點的關系的集中程度，或者是說一個參與者在社會網絡中的主導情況，點中心度越大，此參與者越居于中心位置。總體中心度指的是某節點在整個網絡結構中與其他各個節點的距離，它所反映的是各個參與者之間的關系密切程度，通常使用節點之間的最短路徑來進行衡量。本文主要關注的是某參與者的局部主導性，因此我們將采用節點中心度作為衡量其重要性的標準。

由于核心節點處于社交網絡關系中的核心位置，與很多節點存在多種形式的直接連接，所以可以運用社交網絡中各節點的度數，對節點的節點中心度做最簡單的測量。我們可以通過下面的公式對任意節點i的節點中心度進行計算：

(3)

節點的節點中心度越大，代表其越是該網絡的核心節點。

2.2度的冪率分布

19世紀，著名的經濟學家Pareto在研究了個人財富的統計分布后，提出了著名的帕累托定律(20/80法則)，即80%的社會財富僅僅掌握在20%的人手中。個人財富值X不小于某個特定數值x的概率與x的常數次冪存在著反比關系：

P(X≤x)～k-γ

(4)

1932年，哈佛大學的語言學家Zifi發現如果將單詞出現的頻率按照由小到大的順序進行排列，則每個單詞出現的頻率和其序號存在著類似于帕累托定律的分布：P(k)～k-γ，這就是著名的Zifi分布。在社交網絡、萬維網、以及新陳代謝網絡等網絡中度的分布同樣具有這種冪律分布特性P(k)～k-γ(通常2≤γ≤3)[7]，其中P(k)為度數為k的節點占總節點個數的比率。例如，好萊塢演員合作網絡的度分布中γ=2.3；www萬維網的度分布中γ=2.1；美國西部電力網絡的度分布中γ=4。

2.3社區框架的挖掘

(5)

其中函數max(V)計算了社交網絡的最大度數，Vk為度為k的節點集合。當取得該關鍵子網絡后我們可以使用已有社區挖掘策略對其進行社區挖掘獲得其社區劃分，得到的社區劃分稱之為原社交網絡的社區框架。算法描述如算法1。

我們稱算法1為MCF算法，在之后的實驗中驗證了該社區框架能夠反映一個社交網絡的社區結構概況，如社交網絡中每個社區的相對大小，社區內的聯系緊密程度以及不同社區之間的聯系情況。

算法1MCF(G,r)

1.輸入社交網絡數據G，比率r

4.輸出社區框架P

2.4社區框架的鉆取

在得到社區框架后，如果想得到社交網絡社區結構更加詳細的信息，可以對社區框架進行鉆取，即向社區框架中添加度數較小的點。對于一個新添加的點，為了判定其屬于社區框架的哪一個社區，需要定義一個距離函數來進行判斷。一種最簡單的方式是如果新加入的節點i與社區框架中某一社區p中相連的點有d′個，則節點i到社區的距離為d(i,p)=d′。但是，按其定義如果節點i與社區p越遠，其聯系越緊密，這與直觀感覺是相互違背的。因此，定義社區p與節點i的距離為p中與i相連點的個數d′的倒數，即：

(6)

在對社區框架進行鉆取時，首先向社區框架中添加不屬于社區框架的，但是度數相對于其他節點最大的節點集合Vk，即：

Vk={i|i∈V且i?V′且ki=max(V-V′)}

(7)

其中函數max(V-V′)求得節點集V-V′中節點的最大度數。Vk添加完成，則新產生的社區框架較原社區框架包含更多的社區結構信息。如想獲得社區結構更進一步的信息，則對社區框架繼續添加節點，最終直至將所有節點添加進去，實現對整個網絡的社區劃分，算法描述如算法2。

算法2DCF(P)

1.輸入待下鉆社區框架P

2.求得并添加節點集Vk

(1)對Vk中的每一個節點計算其到社區框架中每個社區的

距離

(2)將Vk中的每一個節點添加到距離其最近的社區

(3)形成新的社區框架P′

3.P=P′

4.如果需要進一步鉆取則跳轉到2繼續執行，否則輸出新的社區

框架P

我們將以上對社區框架進行鉆取的算法2稱之為DCF算法。在DCF算法中計算節點到社區的距離并添加到相應社區的時間復雜度為O(n)。當向社區框架中加入所有節點的時候，便取得了一個對整個社交網絡的社區劃分。對此社區結構劃分的好壞可以通過Q函數來進行評價。

通過使用MCF算法挖掘出社交網絡的社區框架，我們能夠在不對整個社交網絡進行社區劃分的情況下獲得其社區概況，這樣使計算量大為減小。即使用戶想得到更加詳細的社區信息，我們也可以使用DCF算法對已有的社區框架進行可控鉆取獲得，從而使用戶可以從不同層次對社區結構進行考察，最終我們能夠實現社交網絡的社區劃分。下面將通過實驗驗證該方法的有效性。

3實驗結果與分析

3.1實驗數據

實驗使用的數據集是netscinece合作網絡[5]，由Newman于2006年統計得出，該網絡描述了來自不同領域的科學家之間的合作關系。其中包含了1589個節點和2742條邊，如圖2所示，圖中間的黑點部分是由大量的離散點聚集形成。由Newman提出的具有開創性意義的GN社區挖掘策略具有較高的社區挖掘精度，并且得到了相關學者的廣泛認可和應用，所以文中將選用其作為相應的實驗對比算法。

我們首先考察生成社區框架(MCF算法)和實現下鉆(DCF算法)所需時間與GN算法所需時間的對比情況，分析通過社區框架下鉆實現的社區劃分在劃分效果上與GN算法的對比情況。然后考察社區框架能否反映出完整社交網絡的社區概況。

圖2　netscience合作網絡[5]

3.2實驗結果

圖3展示了在netsicence社交網絡中節點的度分布。首先，該社交網絡中度數為3的節點數量最多，其實際意義是與三個人有過合作的學者最多。其次，該社交網絡含有少量的度數比較高的節點，這些節點代表了發表論文比較多且有較高影響力的學者。從圖中的曲線走勢我們可以得出該網絡的節點度分布基本符合冪律分布的特性。

圖3　netscience節點度分布

在MCF算法中，我們按0.2的比率提取關鍵子網絡G′(V,E)，并對其進行社區劃分。得到的關鍵子網絡含有359個節點(占總節點個數的22.59%)，1171條邊(占總邊數的42.71%)，對其使用GN算法進行社區劃分得到了7個大的社區以及大量的小的社區，共49個社區，如圖4所示。隨后在該社區框架基礎之上通過使用DCF算法依次添加V4、V3、V2、V1實現了對整個社交網絡的社區劃分。

圖4　netscience社區框架

表1給出了MCF算法、DCF算法以及使用GN算法直接對整個社交網絡進行社區劃分所需時間的對比情況。通過表1能夠發現社區框架的挖掘所需時間僅為GN算法所需時間的28.1%，對社區框架進行下鉆所需時間為GN算法的34%，總的時間比GN減少40%。

表1　運行時間對比

表2展示了通過下鉆所得社區結構與使用GN算法所得社區結構質量在Q函數上的體現情況。觀察可得GN算法所得到的社區結構在質量方面要略好于通過下鉆所得到的社區，但是兩者差距并不是很明顯。

表2　社區質量對比

綜合表1和表2，本文提出的算法可以在較少的時間上挖掘出一個社交網絡的社區框架，并能夠通過鉆取社區框架實現對整個網絡的社區劃分，而且，社區結構質量接近GN算法所得到的社區結構質量。

下面的實驗通過對比社區結構與社區框架的相關數據，驗證了所得到的社區框架能夠反映整個網絡的社區概況。實驗數據中的社區框架由MCF算獲得，社區結構由DCF對社區框架挖掘獲得。其編號由程序產生。

圖5展示了社區結構與社區框架中對應社區的成員數目的對比情況，從圖中可以看出社區框架中社區的相對大小能夠反映社區結構相應社區的相對大小。例如，社區框架中編號為3、12、46、49的社區是相對較大的社區，而其對應社區結構中的社區也是相應的大社區。

圖5　社區內節點個數對比

圖6展示了社區結構與社區框架的社區內部邊密度對比情況。所謂的社區內部邊密度指的是社區內部邊的條數與社區內部點的個數的商，其在netscience中的現實意義是：在社區內部成員之間的合作密切程度，邊密度越大說明社區成員之間的合作越密切。通過觀察發現圖中兩條曲線基本吻合的，但是也出現了很多不一致的情況，如社區21-28，這種不吻合主要是由社區規模太小，在統計上不準確造成的，通過觀察圖5可以發現社區21-28這幾個社區的規模都非常的小。

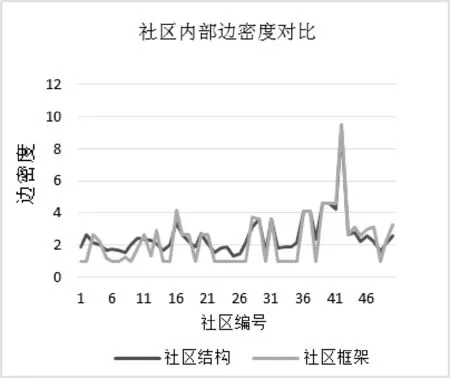
圖6　社區內部邊密度對比

圖7展示了49號社區與其他社區之間的聯系情況，這里僅列出了與之有聯系的社區的編號。通過觀察社區結構所對應的曲線可知，社區49與社區2、22、43、48之間存在聯系，其中與社區48的聯系最為緊密。我們觀察社區框架同樣能夠得到類似的信息，在社區框架中社區49與22、43、48之間存在聯系，其中與社區48聯系最為緊密。

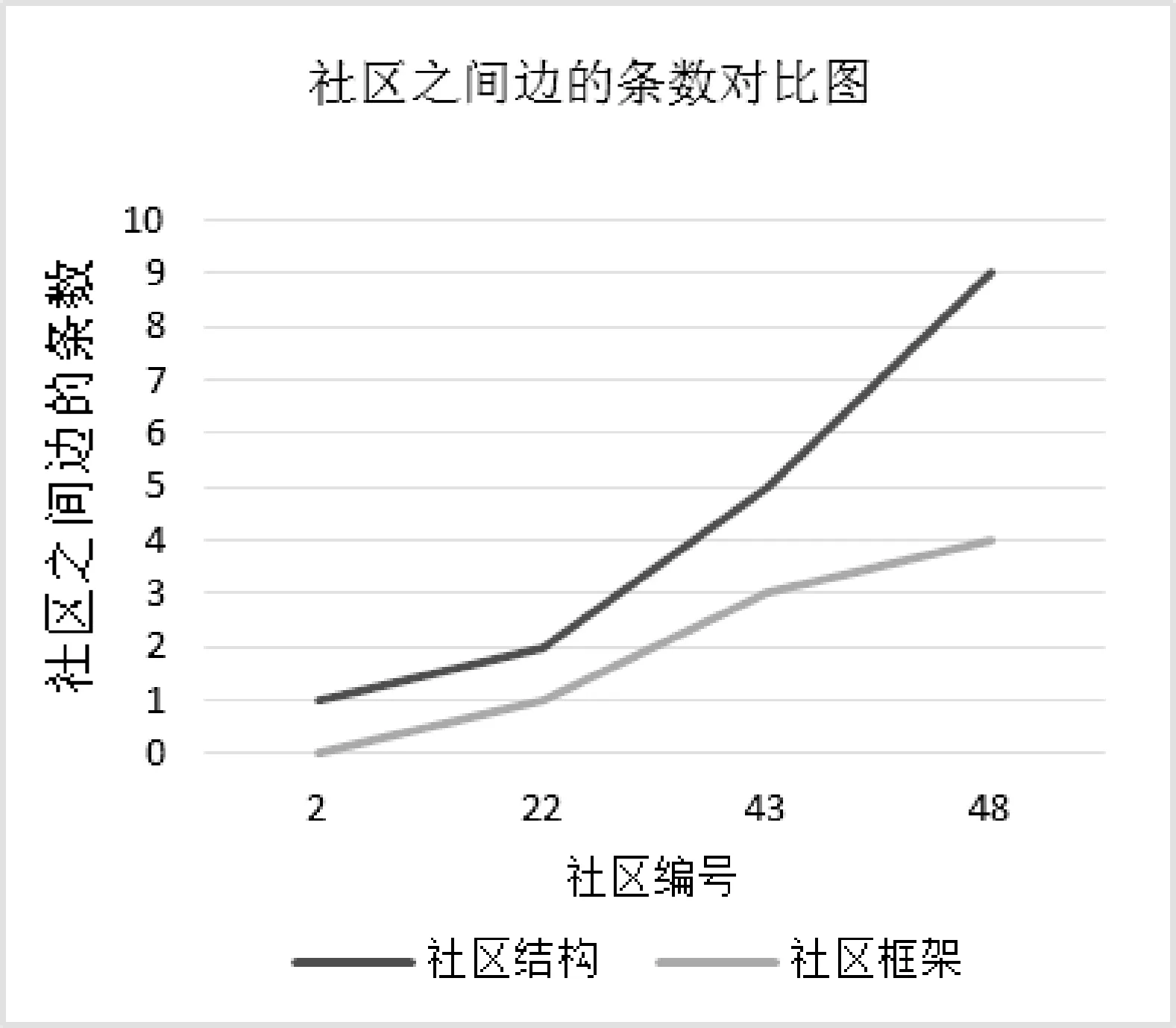
圖7　社區之間邊的條數對比

以上實驗驗證了社區框架能夠反映社交網絡的社區結構的概況，包括社區內部節點的相對多少、社區內部邊的密度、社區之間的聯系緊密程度。

4結語

通過使用MCF算法，我們能夠快速地在不對整個社交網絡進行社區挖掘的情況下了解社區的概況，并能夠使用DCF算法對社區框架進行鉆取，最終實現對社交網絡的社區劃分。最后通過實驗驗證了我們所提方案的有效性。然而，我們最終實現的社區劃分效果相對于成熟的GN算法來說還有待提高，同時我們也發現，本文所提方案只有應用于符合冪律分布的社交網絡時，才會體現出其性能優勢。今后的主要工作是當社交網絡是以加權有向圖表示時，如何可控的快速的發現其社區結構，同時如何利用社交網絡進行高效地廣告分發和流行病控制也是我們感興趣的一個研究方向。

參考文獻

[1] Burt R S,Kilduff M.Social network analysis:Foundations and frontiers on advantage[J].Annual review of psychology,2013,64(2):527-547.

[2] Fortunato S.Community detection in graphs[J].Physics Reports,2010,486(3):75-174.

[3] 竇炳琳,李澍淞,張世永.基于結構的社會網絡分析[J].計算機學報,2012,35(4):741-753.

[4] Girvan M,Newman M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences,2002,99(12):7821-7826.

[5] Newman M E J.Finding community structure in networks using the eigenvectors of matrices[J].Physical review E,2006,74(3):036104.

[6] Opsahl T,Agneessens F,Skvoretz J.Node centrality in weighted networks:Generalizing degree and shortest paths[J].Social Networks,2010,32(3):245-251.

[7] Barabási A L,Albert R.Emergence of scaling in random networks[J].science,1999,286(5439):509-512.

[8] Newman M E J.The structure and function of complex networks[J].SIAM review,2003,45(2):167-256.

[9] 楊博,劉大有,金弟.復雜網絡聚類方法[J].軟件學報,2009,20(1):54-66.

[10] Newman M E J,Girvan M.Finding and evaluating community structure in networks[J].Physical review E,2004,69(2):026113.

收稿日期：2015-01-05。國家自然科學基金項目(61170052)。王童童，碩士生，主研領域：社交網絡，數據挖掘。李盛恩，教授。王剛，碩士生。

中圖分類號TP311.13

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.07.020

MINING COMMUNITY FRAMEWORK BASED ON SOCIAL NETWORKS’ NODE CENTRALITY

Wang TongtongLi Sheng’enWang Gang

(SchoolofComputerScienceandTechnology,ShandongJianzhuUniversity,Jinan250101,Shandong,China)

AbstractAs an important topological characteristic which the real complex networks commonly have, community structure has been widely and thoroughly studied in recent 10 years. To solve the problems of community mining strategy that its time complexity is too high and lacks the interaction with users, etc., we discussed the node centrality, node’s power-law degree distribution and other characteristics of social networks, and proposed the concepts of "critical sub-network" and "community framework". Moreover, we designed the community framework mining (CFM) algorithm and the community framework drilling (CFD) algorithm. Among them, the CFM algorithm is used to mine the community framework of social networks, and CFD is used for drilling the community framework and to demonstrate the community structure from different granularities. Experimental results and analysis showed that, in a relatively short time the CFM algorithm could be used to mine out the community framework reflecting the complex networks community state, while the CFD algorithm could implement high-quality community partition in the way of user interaction.

KeywordsSocial networksCommunity structureNode centralityCommunity frameworkCommunity quality