基于北斗三頻數據的周跳探測與修復

李樂樂，王振杰，賀凱飛

(中國石油大學(華東)，山東 青島 266580)

?

基于北斗三頻數據的周跳探測與修復

李樂樂，王振杰，賀凱飛

(中國石油大學(華東)，山東 青島 266580)

摘要：針對三頻偽距相位法和無幾何相位法通常受電離層影響較大的問題，對其進行改進。選取弱電離層影響、低噪聲的組合觀測值，分析兩種方法共同的不敏感周跳組合；采用LAMBDA方法搜索周跳固定解；采用北斗實測數據進行驗證分析。結果表明：除兩個不敏感周跳組合外，改進后的算法能探測并修復出1周以上的所有周跳。

關鍵詞：北斗；三頻數據；弱電離層組合；周跳探測與修復

周跳探測與修復是數據質量控制的重要組成部分，是實現高精度定位的保證[1]。隨著GNSS技術的發展，北斗衛星導航系統已經能夠播發三頻信號[2-3]。相對于雙頻數據，使用三頻數據可得到電離層延遲誤差更小、噪聲水平更低、波長更長的周跳檢測量[4-6]，它們更好地削弱觀測值的系統誤差，更有利于周跳的探測與修復。

常用的三頻非差數據周跳探測與修復方法主要有：偽距相位法[7-11]和無幾何相位法[11-12]。文獻[7]采用偽距相位法探測并修復任意單一頻率相位觀測值的周跳，但當電離層變化劇烈時，小周跳探測效果并不理想。文獻[10]選取3種線性無關偽距相位組合探測并修復周跳，但其中一個組合受電離層延遲影響大，在電離層變化劇烈的地區，探測精度會降低。文獻[8]對三頻偽距相位法和無幾何相位法進行對比分析，他認為無幾何相位法的探測精度高，但存在不敏感周跳；當忽略電離層變化時，偽距相位組合法可以探測出1周以上的任何周跳，但受偽距噪聲影響大。文獻[12]聯合無幾何相位法和偽距相位法探測并修復出1周以上的周跳，但前提是忽略電離層延遲誤差。

綜上可得，目前三頻數據周跳探測和修復的方法通常受電離層誤差影響較大，在電離層活動平緩時，這些方法較為理想；但當電離層活動劇烈時，其對小周跳的探測效果并不理想。本文對偽距相位法和無幾何相位法進行改進，選取弱電離層延遲影響、低噪聲的組合觀測值，除(3,2,2)、(-3,-2,-2)周跳組合外，可以探測出1周以上的所有周跳；周跳修復時，采用LAMBDA方法搜索周跳固定解；最后，采用北斗實測數據進行驗證分析。

1北斗三頻數據周跳探測與修復原理

1.1偽距相位法

1.1.1偽距相位法的基本原理

根據組合觀測值理論[4-6]，三頻偽距、相位組合觀測方程分別為

(1)

(2)

式中：Pm,n,l是偽距組合觀測值，

其中，m,n,l都是實數；P1,P2,P3是原始偽距觀測值；R是接收機和衛星之間的幾何距離；c是電磁波在真空中的傳播速度；Δtr是接收機的鐘差;Δts是衛星的鐘差；Δρtrop是對流層延遲誤差；I是電離層電子總含量(TEC)的函數；λ是組合波長，

其中，λ1,λ2,λ3是3個頻率載波的波長；φi,j,k是相位組合觀測值，φi,j,k=iφ1+jφ2+kφ3，i,j,k都是整數，φ1,φ2,φ3是以周為單位的原始相位觀測值；N是組合模糊度，

N=iN1+jN2+kN3，

其中，N1,N2,N3是初始模糊度；A，B是電離層延遲系數，

其中，f1，f2，f3是3個載波的頻率；εm,n,l,εi,j,k是偽距、相位組合觀測的噪聲(包括多路徑效應)。

式(1)、式(2)相減且在相鄰歷元之間求一次差得周跳檢測量

(3)

式中：Δ表示在相鄰歷元間求差;Kiono=A+B；ε是組合噪聲。從式(3)可知，偽距相位法的探測精度主要取決于電離層延遲在歷元間的變化、組合波長以及組合噪聲[13]。

1.1.2偽距相位法組合系數的選取

假設原始相位觀測值之間、相位觀測值和偽距觀測值之間不相關，并且偽距、相位觀測值的誤差相等，即σ1=σ2=σ3=σ(以周為單位)，σP1=σP2=σP3=σP(以m為單位)。

由誤差傳播律得

(4)

周跳探測時，當|ΔN|>3σΔN，則判定觀測數據發生周跳。

本文首先選取相位組合系數，然后在相位組合系數固定的情況下，選取偽距組合系數，具體方法：

1)設σ=0.01周，σP=0.5m，以σφi,j,k<0.1，λ>1m，|A|<2，i，j，k∈[-10,10]為約束條件選取相位組合系數。若組合系數符合線性關系，只保留噪聲最小的組合。

2)當采樣間隔較小時，電離層變化速度在3～10mm/s[14]，以30s采樣間隔為例，歷元間電離層變化引起的測距誤差在0.1～0.3m左右，當Kiono<0.001，可以忽略電離層在歷元間的變化。因此，以Kiono<0.001，m，n，l∈[-100,100]為條件，為1)中所有的相位組合選取其對應的最佳偽距組合系數；對每個相位組合而言，滿足條件的偽距組合有許多，本文只選取σΔN最小的組合。

經過上面兩步，可以得到偽距相位法不同的組合系數，表1是不同組合系數的組合觀測值及其屬性。

表1　不同系數的組合觀測值及其屬性

從表1中可以看出，(2,5,-7)組合的電離層延遲系數最小，但是組合噪聲最大；(0,-1,1)、(1,0,-1)、(1,1,-2)、(1,2,-3)、(1,4,-5)組合的電離層延遲系數相差很小，而(0,-1,1)組合的噪聲最小，(1,2,-3)次之；(1,3,-4)組合的電離層延遲系數較小，但是組合噪聲比(1,2,-3)組合略大；以組合噪聲最小為標準，本文選取 (1,2,-3)、(0,-1,1)這兩個組合進行周跳的探測與修復。

以3σΔN為閾值，對于(1,2,-3)組合，3σΔN=1.248>1，1周的周跳不能被探測，2周以上的周跳可以被探測；對于(0,-1,1)組合，3σΔN=0.309<1，1周以上的周跳都可被探測。

1.2無幾何相位法

1.2.1無幾何相位法的基本原理

無幾何相位是指相位組合觀測方程中沒有接收機到衛星的幾何距離，其數學模型滿足

即

(5)

其中，C是組合觀測方程的電離層延遲系數，

式(5)在歷元之間求差得

(6)

定義以周為單位的無幾何相位法的周跳檢測量為

(7)

由誤差傳播律得周跳檢測量的中誤差為

(8)

當組合觀測方程的電離層延遲系數C=0時，可忽略電離層在歷元間的變化對周跳檢測量ΔNα,β,γ的影響，為此無幾何相位法探測出周跳的條件可設為|ΔNα,β,γ|>3σΔNα,β,γ。

1.2.2無幾何相位法組合系數的選取

無幾何相位法的檢測量主要受電離層延遲誤差、組合噪聲的影響。為了消除電離層延遲誤差的干擾，選用消電離層組合，組合系數滿足

(9)

解得

(10)

當γ=1時，α=0.226，β=-1.226，進行單位化得α=0.141，β=-0.767，γ=0.626。此時，3σΔNα,β,γ=0.053 7<1，因此可探測出1周以上的周跳。

1.3不敏感周跳的分析

偽距相位法和無幾何相位法都存在各自的不敏感周跳，但兩者聯合可以減少不敏感周跳，下面進行詳細的分析：

對偽距相位法而言，忽略觀測噪聲和電離層的影響，3個波段上發生的周跳ΔN1,ΔN2,ΔN3與周跳檢測量ΔN滿足

(11)

對(1，2，-3)組合而言，由|ΔN|<3σΔN得ΔN=0或±1。對(0,-1,1)組合而言，由|ΔN|<3σΔN得ΔN=0，因此這兩個組合共同的不敏感周跳滿足如下3種不同的方程組。

(12)

或

(13)

或

(14)

它們的非零解系分別是

(15)

(16)

(17)

對于無幾何相位法而言，忽略相位觀測噪聲和電離層誤差的影響，3個波段上發生的周跳ΔN1,ΔN2,ΔN3與周跳檢測量ΔNα,β,γ滿足

(18)

當|ΔNα,β,γ|<0.053 7，無幾何相位法失效，把式(15)～式(17)分別帶入該不等式得

(19)

(20)

(21)

由式(19)得，ΔN1，ΔN2，ΔN3無非零整數解。

由式(20)得，ΔN1=3，ΔN2=2，ΔN3=2，即當發生(3,2,2)周跳組合時，兩種方法都失效。

由式(21)得，ΔN1=-3，ΔN2=-2，ΔN3=-2，即當發生(-3,-2,-2)周跳組合時，兩種方法都失效。

從以上分析可得，聯合采用偽距相位法和無幾何相位法，除(3,2,2)、(-3,-2,-2)周跳組合之外，可探測出1周以上所有的周跳。

1.4周跳的修復

如果要修復周跳，3組組合系數構成的矩陣必須滿秩[15]。本文選取的組合系數符合要求，組合系數矩陣A、周跳矩陣X和周跳檢測量矩陣L滿足

AX=L.

(22)

采用LAMBDA法[16]搜索周跳的固定解，并以Ratio>2判斷固定解是否可靠。

2實驗驗證與分析

采用北斗實測數據進行實驗，數據采樣間隔為30 s，共574個觀測歷元；實驗分為兩組：第一組是人為添加小周跳、不敏感周跳的測試實驗，第二組是模擬真實周跳的測試實驗，周跳發生的時刻和大小都是隨機添加；兩組測試都是對C01號衛星添加周跳，第一組在第200歷元處添加周跳，第二組是隨機選取10個歷元，隨機添加周跳。圖1～圖8是第一組測試實驗的周跳檢測量隨時間變化圖，表2是該組測試的結果；表3是第二組的測試結果。

圖1～圖3是只有一個組合失效后的檢測量變化圖，圖4～圖6是任意兩個組合失效后的檢測量變化圖；從這6幅圖中可以看出，當發生1周以上的組合周跳，本文選取的3個周跳探測組合至少存在一個組合可以把其探測出來；同時從表2可以看出，添加的周跳都得到準確修復，且Ratio=5.7>2，表明修復值可靠性大。

圖7、圖8分別是添加(-3,-2,-2)、(3,2,2)組合周跳后檢測的變化圖，從圖中可以看出，此時3個周跳檢測量都沒有超過閾值，發生的周跳不能被檢測到，這與前文的分析相吻合。

圖1　添加(4,0,1)周跳的檢測量的變化

圖2　添加(3,1,1)周跳的檢測量的變化

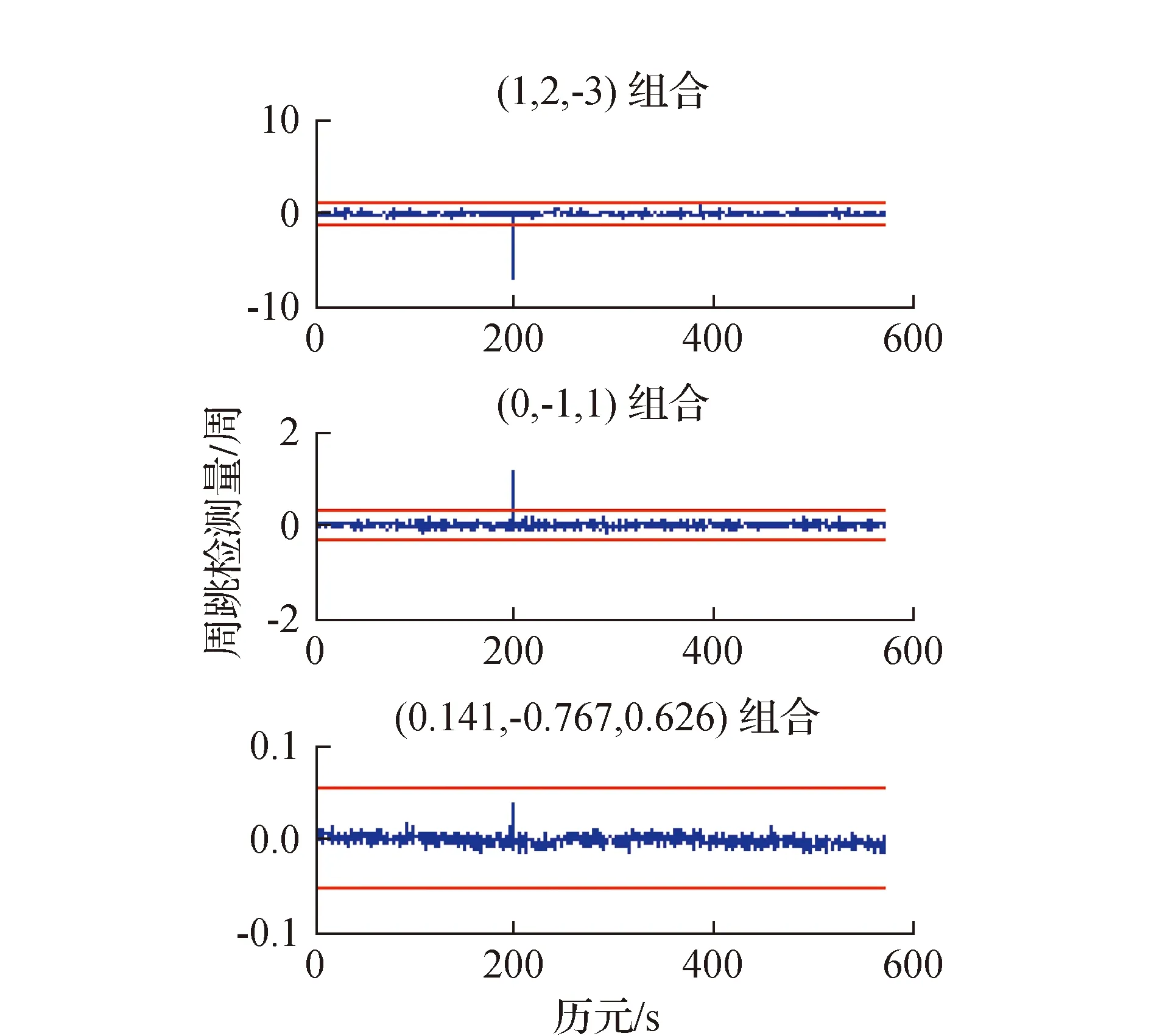
圖3　添加(-2,2,-3)周跳的檢測量的變化

圖4　添加(33,28,30)周跳的檢測量的變化

圖5　添加(1,1,1)周跳的檢測量的變化

圖6　添加(-5,-3,-3)周跳的檢測量的變化

圖7　添加(-3,-2,-2)周跳的檢測量的變化

圖8　添加(3,2,2)周跳的檢測量的變化

模擬周跳組合檢測量值修復值Ratio值(4,0,1)(0.88,1.1,1.3)(4,0,1)5.7(3,1,1)(1.88,0.11,0.19)(3,1,1)5.7(-2,-2,3)(-7.1,1.1,0.04)(-2,-2,3)5.7(33,28,30)(-1.1,2.1,-0.02)(33,28,30)5.7(1,1,1)(-0.12,0.1,-0.08)(1,1,1)5.7(-5,-3,-3)(-2.1,0.1,0.88)(-5,-3,-3)5.7(3,2,2)(0.1,-0.03,-0.05)--

從表3可以看出，隨機添加10組周跳組合后，周跳檢測量值均大于閾值，周跳可被探測出來；同時每一組周跳組合的修復值與添加值相符，而且它們的Ratio值都大于2，保證修復的可靠性。

表3　隨機添加周跳的修復情況

3結論

本文采用聯合偽距相位法和無幾何相位法進行周跳探測和修復，通過選取合適的組合系數構成3組周跳檢測量，最終探測出除不敏感周跳外1周以上的任意周跳；弱電離層延遲影響、低噪聲的組合觀測值減小電離層延遲誤差及觀測噪聲的影響，保證在電離層活動劇烈的情況下周跳探測的精度；采用LAMBDA方法搜索周跳的固定解，同時用Ratio值檢驗修復值，保證修復的可靠性。但是本文選取的第一個組合系數噪聲較大，使得周跳組合(3,2,2)、(-3,-2,-2)成為不敏感周跳，因此需要進一步研究系數選取方法，以便消除不敏感周跳。

參考文獻：

[1]徐園,楊力,耿彥龍.基于多頻載波/偽距數據組合進行周跳探測與修復的實現[J].測繪工程，2012,21(3):49-52.

[2]張暉，陸敏燕.單頻精密單點定位周跳探測方法研究[J].測繪與空間地理信息，2015，38(1)：132-134，140.

[3]TANGW,DENGC,SHIC,etal.Triple-frequencycarrierambiguityresolutionforBeidounavigationsatellitesystem[J].GPSSolutions,2014,18(3):335-344.

[4]韓紹偉.GPS組合觀測值理論及應用[J].測繪學報，1995(2):8-13.

[5]MARCC,STEPHANIEB,OMIDK,etal.Asystematicinvestigationofoptimalcarrier-phasecombinationsformodernizedtriple-frequencyGPS[J].Journalofgeodesy,2008,82(9):555-564.

[6]劉國超,黃張裕,徐秀杰,等.COMPASS三頻數據線性組合優化選取分析[J].測繪工程，2014,23(9):32-35.

[7]周巍，郝金明，馮淑萍.北斗三頻數據周跳的探測方法[J].測繪科學技術學報，2012(2):87-90.

[8]馬威武，徐寅生.GPS三頻無幾何相位組合周跳探測與修復[J].測繪與空間地理信息，2015，38(10)：158-160.

[9]時榮.一種計算北斗三頻多路徑的方法及其結果分析[J].測繪與空間地理信息，2015，38(8)：175-177.

[10] 孫保琪，歐吉坤，盛傳貞，等.一種適于Compass周跳探測的三頻數據優化組合[J].武漢大學學報(信息科學版)，2010(10):1157-1160.

[11] 李金龍，楊元喜，徐君毅，等.基于偽距相位組合實時探測與修復GNSS三頻非差觀測數據周跳[J].測繪學報，2011(6):717-722.

[12] 黃令勇，宋力杰，王琰，等.北斗三頻無幾何相位組合周跳探測與修復[J].測繪學報，2012(5):763-768.

[13] 劉旭春，伍岳，黃學斌，等.多頻組合數據在原始載波觀測值預處理中的應用[J].測繪通報，2007(2):14-17.

[14] 曹新運，王堅.GPS三頻非差觀測值探測與修復周跳[J].武漢大學學報(信息科學版)，2014(4):450-456.

[15]ZHAOQ,SUNB,DAIZ,etal.Real-timedetectionandrepairofcycleslipsintriple-frequencyGNSSmeasurements[J].GPSSolutions,2014:1-11.

[16]ZHEND,KNEDLIKS,LOFFELDO.InstantaneousTriple-FrequencyGPSCycle-SlipDetectionandRepair[J].InternationalJournalofNavigationandObservation,2009:1-15.

[責任編輯：張德福]

DOI:10.19349/j.cnki.issn1006-7949.2016.10.005

收稿日期：2015-07-04；修回日期：2015-10-18

基金項目：國家自然科學基金資助項目(41374008)

作者簡介：李樂樂(1990-)，男，碩士研究生.

中圖分類號：P228

文獻標識碼：A

文章編號：1006-7949(2016)10-0020-06

Circle-slip detection and repair based on Beidou triple-frequency data

LI Lele，WANG Zhenjie，HE Kaifei

(ChinaUniversityofPetroleum,Qingdao266580,China)

Abstract：Considering that code-phase method and geometry-free phase method are usually influenced by the ionospheric delay,this paper has improved these two methods.Combined observations with low ionosphere effect and small noise are selected,and common insensitive circle-slips of these two methods are analyzed.LAMBDA technique is applied to searching the fixed resolutions of circle slips.At last,experiments are carried out with Beidou data.The result shows that circle slips which are greater than 1 circle can be detected and repaired except for two insensitive circle-slips.

Key words：Beidou；triple-frequency data；low ionospheric delay combinations；circle-slip detection and repair