殺爆戰斗部破片與沖擊波運動規律研究*

龔超安,陳智剛,印立魁

(中北大學地下目標毀傷技術國防重點學科實驗室,太原　030051)

?

殺爆戰斗部破片與沖擊波運動規律研究*

龔超安,陳智剛,印立魁

(中北大學地下目標毀傷技術國防重點學科實驗室,太原030051)

摘要:通過對殺爆戰斗部爆炸后破片運動及沖擊波傳播的研究,為提高破片和沖擊波相遇位置的計算精度,理論推導了新的計算方法。采用Visual C++開發破片與沖擊波運動規律計算系統使計算方便。運用ANSYS/LS-DYNA數值模擬了某預制破片戰斗部爆炸后破片與沖擊波的運動,數值模擬與該模型計算結果相符,較以往計算模型精度提高了8.3%。

關鍵詞:破片;沖擊波;運動規律;LS-DYNA

0引言

殺爆戰斗部作為反導戰斗部主要采用的方式,國內外對其研究從未中斷過。殺爆戰斗部對目標主要有三個破壞作用:爆轟生成物的直接作用、沖擊波的破壞作用以及破片的殺傷作用。其中就沖擊波和破片對目標的作用研究較多。作為兩種毀傷元,其對目標的作用原理不同導致作用順序影響毀傷效能[1-2]。因此,破片與沖擊波相遇位置計算的研究極其重要。文獻[3]根據試驗數據對不同比例距離、裝填系數和破片與沖擊波相遇時間進行擬合。沖擊波傳播距離與時間的關系目前沒有準確的表達式,任意時刻破片與沖擊波的距離及位置未有精確計算。

1TNT當量轉換計算

1.1帶殼裝藥等效為裸露裝藥

帶殼炸藥爆炸時,根據能量守恒定律,質量為m的炸藥釋放出的總能量用于爆炸產物的內能和動能的增加,以及破片飛散的動能,即[4]:

mQv=E1+E2+E3

(1)

E1+E2=mQv-E3=mbeQv

帶殼裝藥等效裸露裝藥的當量計算,令β=m/M為裝填系數,對于圓柱形殼體裝藥:

(2)

1.2其他炸藥等效TNT球形裝藥

其他類型的炸藥在無限空氣介質中爆炸轉換為TNT,設某一炸藥的爆熱是Qvi,藥量是mbe,其TNT當量為ω=mbeQvi/QvT,式中QvT為TNT的爆熱。殺爆彈大部分裝藥為圓柱形,沖擊波傳播距離大于裝藥特征尺寸,可近似看成球形裝藥的爆炸。

2沖擊波速度

2.1TNT超壓計算

對于裸露的TNT球形裝藥在無限空氣中爆炸,正壓區峰值超壓為ΔP+,我國國防工程設計規范中規定的計算公式為[4]:

(3)

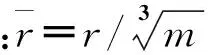
2.2沖擊波超壓與沖擊波速度關系

表征沖擊波超壓與速度關系的蘭金-雨果尼奧(Rankine-Hugoniot)方程[5]為:

(4)

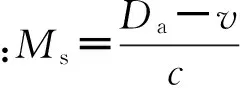
(5)

對上式倒數積分即是時間t與距爆心的距離R的關系。

(6)

由于式(6)解析解非常復雜,給計算帶來困難,文獻[6,8]用擬合式(7)近似代替計算,但此式使用范圍有限,且對裝填比大于1的模型誤差較大。

(7)

在實際計算中,可將式(6)轉化為數值積分。采用劃分區間指定步長,反復積出一系列的點,并繪制成曲線。點的密集度直接反應計算的精度,并由步長體現。式(6)、式(7)與文獻[9]試驗結果對比如圖1所示。

圖1　式(6)、式(7)計算值與試驗值比較

3破片初速及衰減

3.1破片初速

由能量守恒定律和Gurney假設得到的計算破片初速的Gurney公式[4]:

(8)

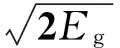
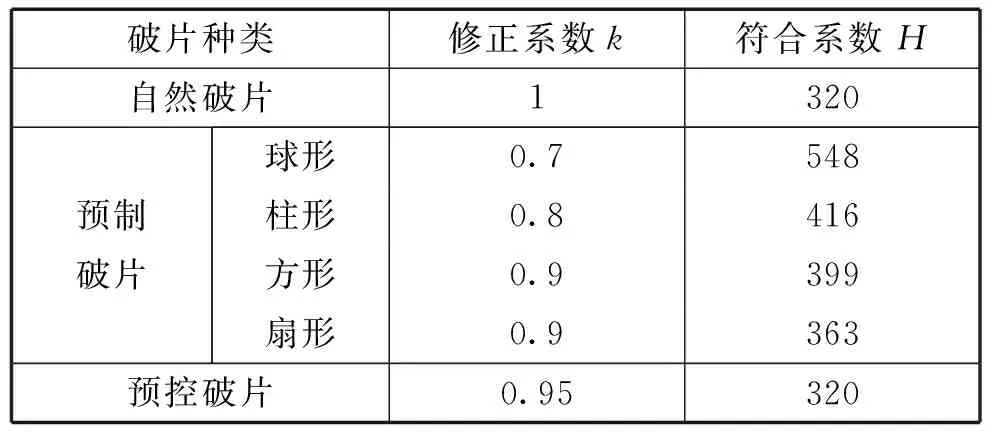
表1　破片初速修正系數及衰減系數

3.2破片速度衰減

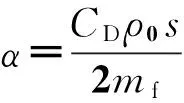
(9)

此關系式按照理論表征破片飛行距離與時間的關系,且對各種破片分別進行計算,比文獻[7-8]采用的近似式(10)適用范圍廣,且在考慮大氣壓力改變的情況下比式(10)精確。

(10)

4破片與沖擊波計算系統

要求破片與沖擊波相遇位置,鑒于理論的真實性和計算的方便性,采用Visual C++開發破片與沖擊波位移時間計算系統。數據處理及界面由MFC控制,坐標系繪圖用TeeChart控件完成。該計算系統框架結構流程如圖2所示。

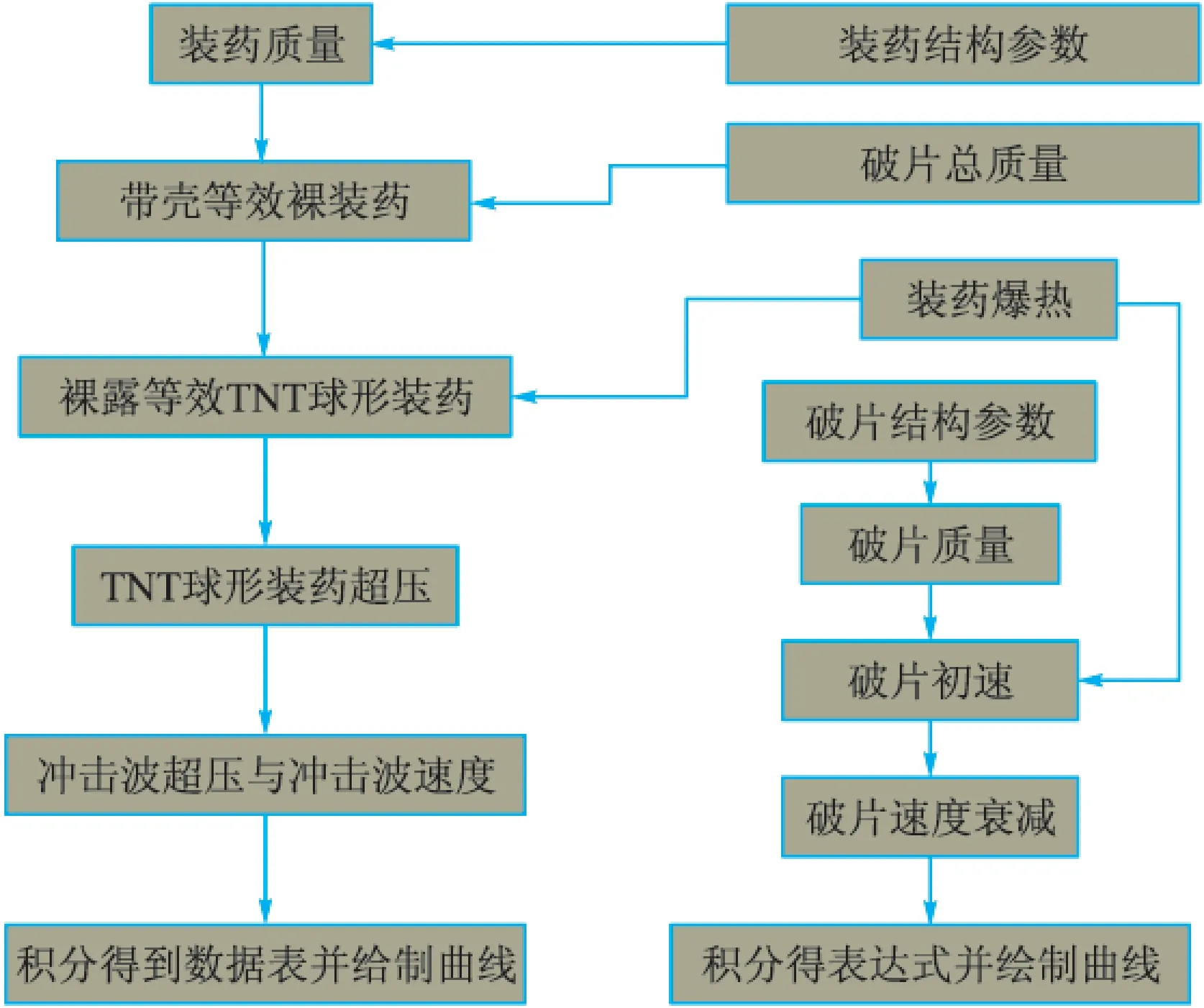
圖2　破片與沖擊波計算系統結構

5實例分析

某殺爆戰斗部TNT圓柱形裝藥半徑為4.8 cm,藥柱高50 cm,單個預制方塊鋼破片質量為0.04 kg,破片沿軸向22層,每層42個,總破片質量為37 kg。

5.1按照以往計算方法

1)破片初速計算

2)飛行距離為L的飛行時間

3)等效TNT當量

1.502kg

4)沖擊波傳播至L處的時間ta

5)沖擊波與破片相遇

令T=ta得出L=4.30m

5.2文中方法

將各參數代入計算系統如圖3。

生成曲線見圖4,起爆后破片與沖擊波的運動分為兩個階段,第一階段:開始沖擊波速度大于破片速度,沖擊波在前,破片在后;第二階段:沖擊波速度衰減比破片速度衰減快,破片與沖擊波相遇后,破片在前沖擊波在后。破片在前期速度衰減較小,與沖擊波在7.1ms時刻相遇于距爆心4.73m處。

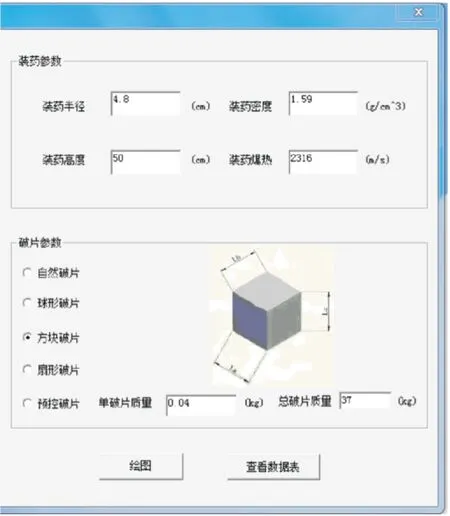
圖3　各參數輸入窗口

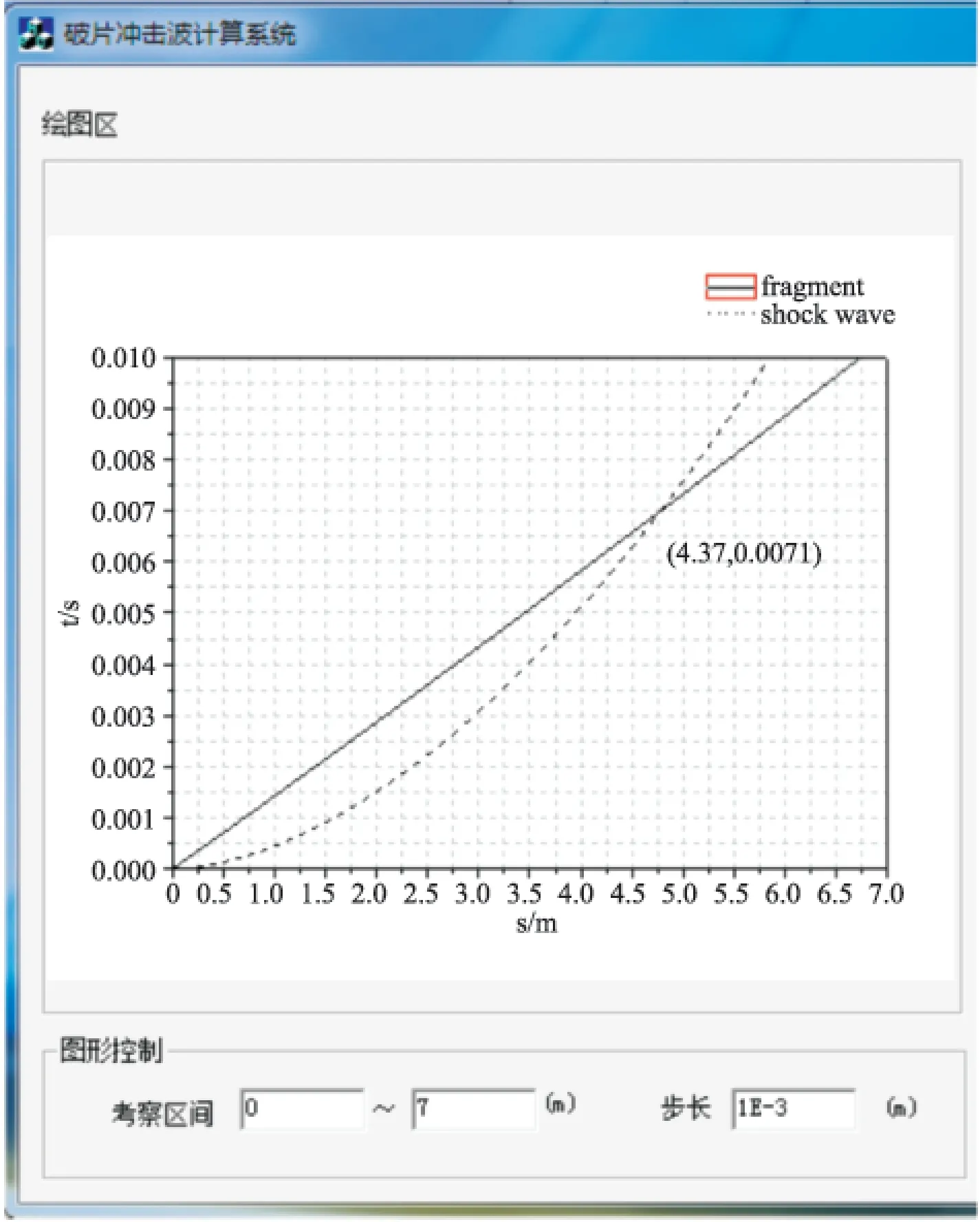
圖4　破片與沖擊波運動時間位移曲線

5.3破片與沖擊波相遇數值模擬

文中運用ANSYS-LSDYNA軟件對裝藥爆炸驅動破片運動進行仿真。由于結構對稱,采用1/4建模簡化計算,炸藥和空氣采用多物質ALE體單元,破片采用Lagrange體單元,ALE體單元和Lagrange體單元之間進行流-固耦合。建7m半徑的空氣域,沖擊波由空氣域內壓力體現。裝藥TNT密度為1.63g/cm3,其本構關系的描述選用MAT_HIGH_EXPLOSIVE_BURN形式,狀態方程采用JWL狀態方程,起爆方式為點起爆;鋼破片密度7.83g/cm3,本構方程選用Johnson-Cook模型,狀態方程為Gruneisen方程。仿真結果的為壓力云圖(見圖5),壓力峰值處為沖擊波位置,破片也運動到該位置,在7ms時刻破片與沖擊波于4.96m處相遇。

圖5　7 ms時刻破片與沖擊波相遇

破片類型相遇位置/m原方法文中方法仿真結果偏差/%方塊4.304.734.698.3%

表2對3種方法的結果進行對比,以數值模擬為準,原方法偏差為8.3%,文中計算方法與數值模擬結果相接近。對于預制破片,部分爆轟產物從預制破片間隙穿過,對沖擊波有加強作用,使沖擊波在第一階段的位移增加,相遇距離變大。

6結語

1)此計算全過程皆有理論依據,適用于所有模型,提高了計算精度。并將預制破片與自然破片用初速修正系數分開計算,避免了按照以往計算結果相同。

2)曲線中任意時刻破片與沖擊波的距離都可讀出,破片與沖擊波運動的兩個階段特點都反映在曲線中,更能準確控制破片與沖擊波對目標的作用順序及距離。

參考文獻:

[1]董秋陽. 機翼蒙皮在破片和沖擊波作用下的損傷研究 [D]. 南京: 南京航空航天大學, 2013.

[2]任丹萍. 破片和沖擊波復合作用下對導彈的毀傷 [D]. 南京: 南京理工大學, 2006.

[3]劉水江. 復合防破片板防護性能分析及數值模擬 [D]. 武漢: 武漢理工大學, 2007.

[4]隋樹元, 王樹山. 終點效應學 [M]. 北京: 國防工業出版社, 2000: 290-292.

[5]張寶平, 張慶明, 黃風雷. 爆轟物理學 [M]. 北京: 兵器工業出版社, 2009: 54-57.

[6]STARKSMW.Vulnerabilityscience,aresponsetoacriticismoftheballisticresearchhaboratoey’svulnerabilitymodelingstrategy:AD-A224785 [R].ArmyBallisticResearchLab, 1990.

[7]曾首義, 蔣志剛, 陳斌, 等. 沖擊波與破片共同作用探討 [C]∥中國土木工程學會防護工程分會第九次學術年會論文集, 2004: 263-367.

[8]梁為民, 張曉忠, 梁任發, 等. 結構內爆炸破片與沖擊波運動規律試驗研究 [J]. 兵工學報, 2009, 30(S2): 289-292.

[9]NorrisJHuffington,WilliamOEwing.Reflectedimpulsenearsphericalcharges:AD-A160 797 [R].ArmyBallisticResearchLab, 1985.

*收稿日期:2015-04-16

作者簡介:龔超安(1990-),男,四川儀隴人,碩士研究生,研究方向:彈箭控制與高效毀傷。

中圖分類號:TJ410

文獻標志碼:A

Research on Motion Law of Fragment and Shock Wave of Blast Fragmentation Warhead

GONG Chaoan,CHEN Zhigang,YIN Likui

(National Defense Key Subject Laboratory of Underground Target Damage Technology, North University of China, Taiyuan 030051, China)

Abstract:According to study of shock wave propagation and fragment movement after explosion of blast fragmentation warhead, a more accurate way was provided for calculation of fragments and shock wave propagation distance and the time delayed. A computing system of fragments and shock wave’s movement was developed by using Visual C++. It makes calculation be more convenient. Movement of preformed fragments and shock wave after explosion was simulated. The results show that the simulation tally with the new calculation model and the accuracy is improved by 8.3%.

Keywords:fragment; shock wave; motion law; LS-DYNA