Besov空間到Bloch型空間上的復合積分算子

陳鵬勇，呂小芬

（湖州師范學院理學院，浙江湖州313000）

Besov空間到Bloch型空間上的復合積分算子

陳鵬勇，呂小芬

（湖州師范學院理學院，浙江湖州313000）

討論了Bloch型空間以及Besov空間到小Bloch型空間上復合積分算子的有界性和緊性特征，得到了該算子為有界算子和緊算子的充要條件.

Besov空間；Bloch型空間；復合積分算子

MSC 2010：47B38

0 引言

設H D（）表示單位圓盤D上全純函數的全體，H D，D（）表示D上全純自映射的全體.給定0＜p＜∞，D上的Besov空間Bp定義為：

給定［0，1）上的連續正值函數μ，若存在常數0≤δ＜1，0＜a＜b，使得

則稱μ為正規權函數.進一步，令μ（z）=μ（z ），?z∈D.定義D上的μBloch型空間

定義小μBloch型空間βμ，0為：

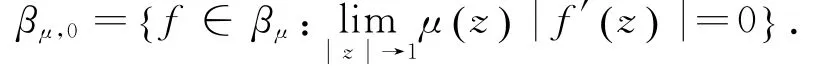
μBloch型空間最早是由胡教授和王教授引入的［1］.易知，在范數‖.‖βμ下βμ是Banach空間，且βμ，0為βμ的閉子空間.事實上，當μ（z）=（1-z2）α時為α-Bloch空間［2-3］.進一步地，若α=1，即為經典Bloch空間［4-5］.

給定g∈H（D）和φ∈H（ D，D），定義H（D）上的復合積分算子Tg，φ為：

注意到，取φ（t）=t，Tg，φ就是已被大家廣泛研究的廣義Cesaro算子［58］等.在文獻［9］中，劉永民等研究了F（p，q，s）空間到對數Bloch空間上復合積分算子Tg，φ的有界性和緊性.于燕燕在文獻［10］中討論了對數Bloch空間到Bloch空間上算子Tg，φ的特性.本文主要研究討論Besov空間到Bloch型（以及小Bloch型）空間上算子Tg，φ的有界性和緊性.

在本文中，C表示與所研究的函數無關的正常數，且每處出現未必同一，符號A≈B表示存在C使得

1 主要結論

下面研究Besov空間到Bloch型（以及小Bloch型）空間上復合積分算子Tg，φ的有界性和緊性.首先給出緊算子的判別方法.

引理1［11］設T：X→Y是有界線性算子，若｛fj｝?X滿足：①‖fj‖X≤C；②當j→∞時，fj在D上內閉一致收斂于0，總有‖Tfj‖Y=0.則T：X→Y為緊算子.

定理1 設g∈H（D），φ∈H（ D，D），0＜p＜∞，則

（1）Tg，φ：Bp→βμ為有界算子當且僅當

進一步地，

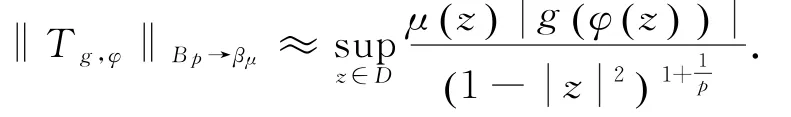
（2）Tg，φ：Bp→βμ，0為有界算子當且僅當→βμ有界且

（3）Tg，φ：Bp→βμ（或βμ，0）為緊算子當且僅

證明 （1）對于任一f∈Bp，由文獻［12］可知：

所以

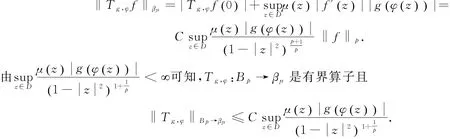
反之，若Tg，φ：Bp→βμ為有界算子.對于任意w∈D，令

則

由文獻［12］可得fw∈Bp，且‖fw‖p＜∞.因此，由Tg，φ的有界性得：

而

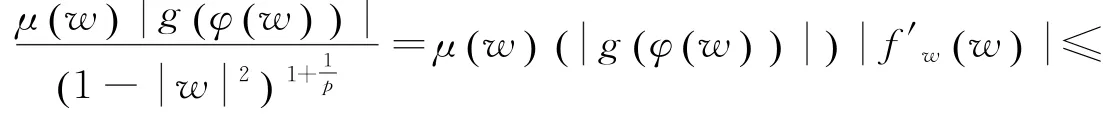
因此

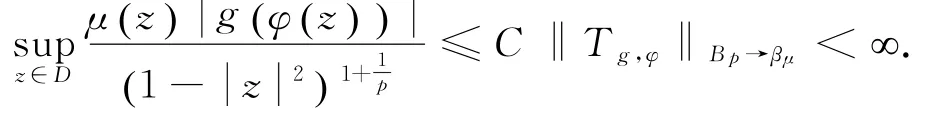
由上述證明可得：

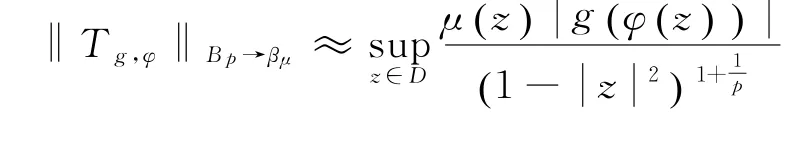
成立.

（2）設Tg，φ：Bp→βμ，0為有界算子.由（1）可知，Tg，φ：Bp→βμ是有界算子.取f≡1，則f∈Bp，Tg，φ1

反之，若Tg，φ：Bp→βμ為有界算子，且limμ（z）g（φ（z））=0.故對任意的多項式p，有：

z→1

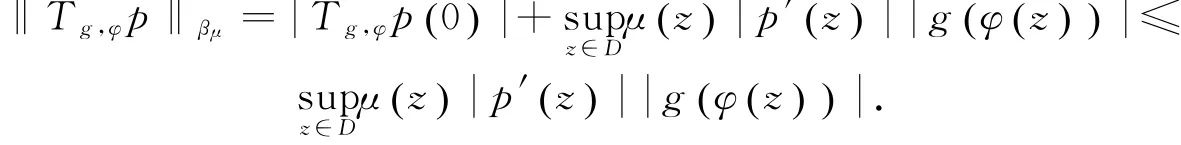
由于βμ，0是βμ中的一個閉子集，可知Tg，φBp?βμ，0.所以Tg，φ：Bp→βμ，0為有界算子.

（3）首先證明Tg，φ：Bp→βμ為緊算子.由于，則?ε＞0，?δ∈（0，1），使得當z＞δ時，總有：

設｛fk｝k∈?是Bp中的范數有界序列，且當k→∞時，fk在D上內閉一致收斂于0.由于fk是全純函數，且｛fk｝在D上內閉一致收斂于0，當k→∞時，有內閉一致收斂于0.所以存在自然數K，對所有的k＞K都有：

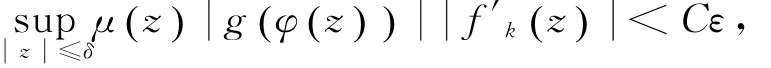
其中C與ε無關.因此

下面證明Tg，φ（Bp）?βμ，0.事實上，?f∈Bp，有：

所以Tg，φf∈

反之，任取｛zk｝k?D滿足|zk|=1.令

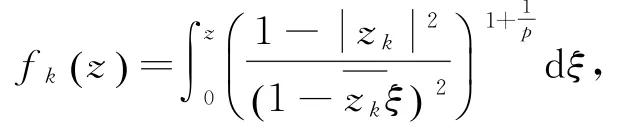
則｛fk｝?Bp且‖fk‖p≤C.而當z ≤δ，δ∈（0，1）時，

所以當k→∞時，f'k在D上內閉一致收斂于0，從而可知fk在D上也內閉一致收斂于0.又因為Tg，φ是緊算子，所以‖Tg，φfk‖βμ→0（ k→∞）.因此當k→∞時，

由于zk｛｝是任取且.定理得證.

［1］HU Z J，WANG SS.Composition operators on Bloch-type spaces［J］.Proc Roy Soc Edinburgh Sect A，2005，135（6）：1 229-1 239.

［2］LI S X，STEVIC S.Generalized weighted composition operators fromα-Bloch spaces into weighted-type spaces［J］.J Inequal Appl，2015，265：12.

［3］肖杰，譚海歐.論p-Bergman spaces，α-Bloch，小α-Bloch空間與Cesàro平均［J］.數學年刊，1998，19（2）：187-196.

［4］MADIGAN K，MATHESON A.Compact composition operators on the Bloch space［J］.Trans Amer Math Soc，1995，347（7）：2 679-2 687.

［5］ZHUO Z Y，YE S L.Volterra-type operators from analytic Morrey spaces to Bloch space［J］.J Integral Equations Appl，2015，27（2）：289-309.

［6］TANG X M.Essential norm of extended Cesàro operators from F（p，q，s）space to Blochtype space［J］.J Comput A-nal Appl，2015，19（2）：335-345.

［7］LIANG Y X，ZHOU Z H，CHEN R Y.Product of extended Cesàro operator and composition operator from the logarithmic Bloch-type space to F（p，q，s）space on the unit ball［J］.J Comput Anal Appl，2013，15（3）：432-440.

［8］LYU X F.Extended Cesàro operators and multipliers on BMOA［J］.Acta Math Sci Ser B，2012，32（2）：559-567.

［9］ZHANG F，LIU Y M.Volterra composition operators from F（p，q，s）to logarithmic Bloch spaces［J］.J Comput Anal Appl，2015，19（3）：444-454.

［10］于燕燕.從對數Bloch空間到Bloch空間上的vollterra型復合算子［J］.數學年刊，2009，27（3）：1 311-1 320.

［11］RUDIN W，劉培德.泛函分析（第2版）［M］.北京：機械工業出版社，2004.

［12］呂小芬.加權Bergman空間到Bloch型空間的廣義Cesaro算子［J］.湖州師范學院學報，2007，29（2）：16-20.

Composition Integral Operators from Weighted Besov Space to Bloch Space

CHEN Pengyong，LYU Xiaofen
（School of Science，Huzhou University，Huzhou 313000，China）

In this paper，we discuss the boundedness and compactness of the composition integral operators from Besov spaces to Bloch spaces or from Besov spaces to little Bloch spaces，and the conclusion is the composition integral operators become the necessary and sufficient conditions for these operators to be bounded or compact.

Besov spaces；Bloch spaces；composition integral operators

O174.56

A

1009-1734（2016）04-0014-04

［責任編輯 高俊娥］

2016-03-10

國家數學天元基金（11526089）；浙江省自然科學基金（LY15A010014）.

呂小芬，副教授，研究方向：函數空間與算子理論.Email：lvxf@zjhu.edu.cn

MSC 2010：47B38