云計算環境中基于策略的多用戶全同態加密方法

劉　青,李陶深，2,黃汝維,2

(1.廣西大學計算機與電子信息學院, 廣西南寧530004;2.廣西高校并行與分布式計算技術重點實驗室, 廣西南寧530004)

?

云計算環境中基于策略的多用戶全同態加密方法

劉青1,李陶深1，2,黃汝維1,2

(1.廣西大學計算機與電子信息學院, 廣西南寧530004;2.廣西高校并行與分布式計算技術重點實驗室, 廣西南寧530004)

摘要:全同態加密技術是解決云環境隱私安全問題的有效方法。考慮云環境下用戶多樣性特征，提出基于策略的多用戶全同態加密方案(PB-MUFHE)，該方案在全同態加密算法的基礎上，通過在密文中設定適當的訪問策略以及在密鑰中設定屬性，從而滿足多用戶密文的全同態運算以及多用戶共享，并支持細粒度的訪問控制。安全分析證明PB-MUFHE可以抵制共謀攻擊，且在LWE困難度假設隨機域模型下是IND-CPA安全的。性能評估表明：PB-MUFHE高效地實現密文數據的全同態運算，并能有效地支持訪問控制和多用戶共享。

關鍵詞:云計算；全同態加密；多用戶；基于屬性加密；密文策略訪問控制

云計算作為一種遠程服務模式，云端數據在被檢索和計算時，有泄露數據的危險。近年來，谷歌郵箱數據泄露，云存儲服務商Dropbox賬戶被盜，蘋果云服務iCloud用戶照片泄露等事件的發生讓人們對云計算的安全性產生了質疑，隱私安全問題嚴重制約了云計算的發展。通常，保護用戶隱私的一種有效方法是加密，但目前大多數加密技術并不支持對密文的計算，因而不能滿足云環境下的隱私安全需求。近年來，全同態加密技術發展迅速，它不僅滿足傳統加密功能，還滿足對密文的計算。全同態加密技術支持密文運算、檢索、排序，能夠保證傳輸、內存、外存上的安全，被廣泛應用于電子股票、醫療、安全多方計算等各個領域。理論上，全同態加密技術很適合解決云環境隱私安全問題。但是基于云環境的復雜性，用戶多樣性，針對單一數據接收用戶的全同態加密方案可能不滿足云環境安全需求。

考慮以下場景，公司員工基于他們的部門和員工等級被限制訪問公司數據，而該公司選擇委托云服務提供商的計算資源來完成公司的大型計算任務，公司中的數據發送者是獨立的且不會意識到公司其他數據發送者的存在。為了遵守公司的隱私規范，每個數據發送者必須設定適當的訪問策略來加密數據，且員工訪問該數據必須滿足加密數據認證條件。不同部門員工上傳的加密數據之間可能會被發送者的子集或者其他授權人員進行計算或者其他處理。當計算后的數據返回給公司時，只有滿足結果數據訪問策略的員工才能有資格對結果數據進行訪問。

針對上面場景，本文提出基于策略的多用戶全同態加密方案(PB-MUFHE)，支持多用戶的密文計算以及多用戶共享，支持對密文細粒度的訪問控制。該方案能夠抵制共謀攻擊，在LWE困難度假設隨機域模型下滿足IND-CPA安全，適于解決云環境下的隱私安全問題。

1相關研究工作

全同態加密的含義是在對明文加密后，能夠在不解密的情況下，對密文進行任意運算，即對于任意有效的運算f及明文μ，有性質f(Enc(μ))=Enc(f(μ))。若f只滿足加法運算或者乘法運算，則稱為加法同態或乘法同態，只有同時滿足加法同態和乘法同態并且滿足緊湊性才能稱為全同態。第一個全同態加密方案是Gentry于2009年提出的[1]，之后人們提出了一些全新構造或改進優化的全同態加密方案。

1.1全同態加密方案

文獻[1～7]在假設稀疏子集和的前提下，基于壓縮技術和同態自解(bootstrapping)技術實現了支持無限次全同態運算的純(pured)全同態加密，這些方案構造方式復雜，密文計算復雜度高。文獻[8～11]在容錯學習(learning with error,LWE)問題或環LWE問題假設基礎上，基于重線性化技術[8]、模尺寸還原技術[8]、密鑰交換技術[9]、模交換技術[9-10]以及張量技術[11-12]等實現了支持多次全同態運算的層次(leveled)全同態加密，這些方案密文計算效率更高，安全性更高，但公鑰尺寸大。以上方案的關注點是：密文的全同態運算次數和效率，公鑰和密文尺寸大小；并且只設定單獨的目標接受者，并不適合上面提到的場景，主要是未考慮在實際應用環境中可能涉及多用戶需求，如訪問控制、多用戶共享以及多用戶密文計算等。

1.2支持訪問控制和多用戶共享的全同態加密方案

文獻[12]基于近似特征向量技術實現了層次全同態加密方案，并提出基于身份、屬性全同態加密技術以支持多用戶共享，滿足相同身份、屬性密文計算。文獻[13]構造了基于訪問策略的全同態加密方案，支持多用戶共享以及不同用戶密文的運算，但該方案構造復雜。文獻[14]提出基于身份的純全同態加密方案，滿足多用戶共享和不同身份、不同屬性密文計算，但該方案嚴重依賴不可區分性模糊能力，導致效率很低。文獻[15]在文獻[12]基礎上提出基于多身份、多密鑰的層次全同態加密方案，滿足多用戶共享，不同身份密文計算。文獻[16]提出構造效率更高的基于身份全同態加密方案，滿足了多用戶共享以及相同身份密文計算。文獻[17]基于密鑰共享方式實現了多用戶全同態加密，滿足多用戶共享，該方案采用對稱加密方式容易使得密鑰泄露。文獻[18]基于抽象代數度量空間技術和加密代理技術構造了多用戶全同態加密方案，滿足多用戶共享。

在以上的方案中，基于身份、屬性加密方式與全同態加密的結合會更合適，原因在于：密鑰共享方式安全性不夠，容易串謀；加密代理方式計算開銷大；基于身份、屬性加密方式開銷小，數據機密性好。對于密文計算問題，文獻[12～16]提出的方案有兩個缺陷：其一，包含屬性、身份的密文參與了密文的計算，這些身份、屬性信息增大了密文尺寸和公鑰尺寸，降低了密文計算效率；其二，可以在未經數據擁有者許可下對任何密文進行計算，這有剽竊用戶數據嫌疑。

針對云環境下用戶多樣性，權衡以上方案的利弊，本文將提出一種基于策略的多用戶全同態加密方案。

2問題描述

2.1云環境中支持隱私保護的計算模型

云環境中支持隱私保護的計算模型如圖1所示，它反映了數據擁有者、用戶、認證中心以及云端之間的交互。模型的具體操作流程如下：

①認證中心使用setup算法生成云計算模型中的公共參數pp和主密鑰msk。

②數據擁有者請求認證中心提供加密公鑰支持，認證中心使用PubGen算法返回公鑰給數據擁有者。數據擁有者使用Enc算法對敏感數據m(i)加密得到密文C(i)。然后將密文C(i)存儲到云端。

③用戶請求認證中心提供私鑰或計算密鑰支持，認證中心針對用戶使用PrvGen算法返回私鑰prvKey給用戶。

④用戶上傳運算符號f，云端根據運算符號，使用Compute算法,對C(i)進行處理，得到結果密文Cresult。

圖1　云環境中支持隱私保護的計算模型

⑤用戶使用私鑰prvKey，根據算法Dec驗證解密權限，對Cresult進行解密，得到結果明文result。

在這個過程中，由于數據擁有者對敏感數據進行了加密，使得用戶隱私得到保護，且滿足密文計算。但這也帶來一些新的問題：其一，云服務可以在未經數據擁有者授權情況下對任何密文進行計算處理，這有剽竊用戶數據的嫌疑，假如云提供商擁有解密密鑰，這相當于云環境下的內部攻擊；其二，密文計算是否滿足多用戶密文計算，這關系到用戶需求滿意度；其三，該模型應用到大型組織時，對于多用戶共享問題，不能很好地解決。因此，本文提出的基于策略的多用戶全同態加密方案PB-MUFHE是解決這些矛盾的關鍵技術。

2.2基于策略的多用戶全同態加密方案

定義1基于策略的多用戶全同態加密方案基于策略的多用戶全同態加密方案εpb-mufhe{Setup, PubGen, PrvGen, Enc, Dec, Compute}是由一組概率多項式時間(PPT)算法組成：

①啟動算法Setup為所有用戶生成公共參數pp以及主密鑰msk, (pp,msk)←Setup(params),params是安全參數；

②公鑰生成算法PubGen為數據擁有者生成公鑰pubKey, pubKey←PubGen(pp),pp是公共參數；

③密鑰生成算法prvGen為用戶生成解密密鑰prvKey和計算密鑰evalKey, (prvKey, evalKey)←prvGen(pp,msk,attrs),attrs為一組屬性串；

④加密算法Enc可能為概率算法，D為明文數據的定義域，對于數據μ∈D,C←Enc(pubKey, policy,μ), policy為訪問策略，μ為明文數據；

⑤解密算法Dec為確定性算法，對于密文C，μ∪{⊥}←Dec(prvKey,C),⊥表示無解；

⑥密文計算算法Compute可能為概率算法，對于密文集合{C1,C2, …,Cl}, Compute′(Dec(prvKey1,C1), Dec(prvKey2,C2), …, Dec(prvKeyl,Cl),op)←Dec(prvKey, Compute(op,C1,C2, …,Cl, evalKey1, evalKey2, …, evalKeyl)),op為運算符，Compute′是與Compute對應的對明文數據運算的算法。

定義2正確性基于策略的多用戶全同態加密方案εpb-mufhe{Setup, PubGen, PrvGen, Enc, Dec, Compute}是正確的：

①?μ∈D,?Dec(prvKey, Enc(pubKey, policy,μ))=μ;

②?{μ1,μ2,…,μl}(μi∈D), ?Compute′(op,μ1,μ2, …,μl)=Dec(prvKey, Compute(op, Enc(pubKey1, policy1,μ1), Enc(pubKey2, policy2,μ2), …, Enc(pubKeyl, policyl,μl), evalKey1, evalKey2, …, evalKeyl))。

定義3安全性基于策略的多用戶全同態加密方案εpb-mufhe{Setup,PubGen, PrvGen,Enc,Dec,Compute}是安全的：

①εpb-mufhe能夠抵御共謀攻擊；

②εpb-mufhe在LWE困難度假設隨機域模型下是IND-CPA安全的。

3基于策略的多用戶全同態加密方案(PB-MUFHE)

本文將構造一種基于策略的多用戶全同態加密方案(PB-MUFHE)。該方案在確保數據擁有者和用戶數據安全的前提下，支持密文的訪問控制，多用戶密文的加法、乘法運算以及多用戶共享。下面詳細介紹PB-MUFHE方案。

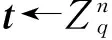
②PubGen(pp)。首先生成矩陣B←以及向量e←χm。再計算向量b=Bt+e。最后生成矩陣A=(b|B)。輸出公鑰pubKey=(mpk, Er, A)。

④Enc(pubKey, policy,μ)。該算法的具體步驟如下：

輸出密文C= (Ct, Cμ)。

⑤Dec(prvKey,C)。該算法的具體操作步驟如下：

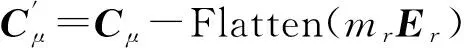
一種熏熏然的氣息彌漫于湖畔的綠樹之間，是這夏末植物的芬芳與醉湖水波氤氳在一起，令人心神激蕩？還是高志明被剛才那股眼波撞擊，醉了？

⑥Compute(policy,op,C1,C2, evalKey1, evalKey2)。算法的具體操作步驟如下：

首先調用policyDec算法驗證計算密鑰evalKey是否滿足密文C1和C2的訪問控制，滿足則解密C1和C2的訪問控制密文Ct，得到r1和r2，若不滿足，則輸出⊥。

4PB-MUFHE的正確性和安全性

定理1PB-MUFHE=(Setup,PubGen, PrvGen, Enc, Dec, Compute)是正確的，如果滿足如下條件:

①?μ∈Zq, ?Dec(prvKey, Enc(pubKey, policy,μ))=μ;

②?{μ1,μ2, …,μl∈Zq}，?Compute′(μ1,μ2, …,μl,op)=Dec(prvKey, Compute(policy,op, Enc(pubKey1, policy1,μ1), Enc(pubKey2, policy2,μ2),…, Enc(pubKeyl, policyl,μl), evalKey1, evalKey2, …, evalKeyl))。

①Dec算法包括兩部分：解密訪問控制密文Ct和數據密文Cμ，解密Ct是解密Cμ的基礎，只有解密Ct正確得到mr，才能正確解密Cμ。

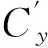
因此，?μ∈Zq, ?Dec(prvKey, Enc(pubKey, policy,μ)=μ。

②Compute算法也包括三部分：對密文進行訪問控制認證、建立新的訪問控制以及密文加法和乘法運算。

對密文進行訪問控制認證，由計算密鑰evalKeyi對訪問密文Ci訪問控制部分密文Ct進行解密得到r1,r2, …,rl，該過程和命題(1)的證明過程相同。

綜上所述，PB-MUFHE是正確的。

定理2PB-MUFHE是安全的，如果滿足如下條件：

①PB-MUFHE能夠抵制共謀攻擊;

②設q=q(λ,L),m=m(λ,L)=O(nlogq),n=n(λ,L), 錯誤分布χ=χ(λ,L), PB-MUFHE在LWE困難度假設隨機域模型下是IND-CPA安全的。

證明：

因此，PB-MUFHE能夠抵制共謀攻擊。

②初始游戲，包含一個IND-CPA攻擊者A，優勢AdvGame[A]表示A在Game中獲勝的概率。

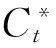
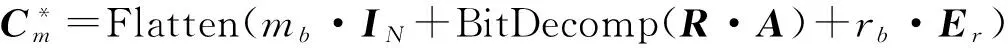
因此，PB-MUFHE是IND-CPA安全的。

綜上所述，PB-MUFHE是安全的。

5PB-MUFHE的性能分析

本方案測試環境是在32位Ubuntu系統(內存1.5 G，CPU 2.27 GHz)，方案實現采用基于512位有限域的超奇異曲線y2=x3+x上的一個160位的橢圓曲線群作為雙線性映射群。

①設參數q=216,n=16,m=256。圖2和圖3是實驗測試數據圖，從圖2中可以看出，PB-MUFHE的加密時間隨著訪問策略的復雜而增加，密鑰生成時間隨著屬性的復雜而增加。

②將本文方案中訪問策略樹中葉子結點個數設為2，密鑰中屬性個數設為1，根據參數n的取值不同，將本文的PB-MUFHE方案與文獻[12]中提出的GSW方案進行加密、解密、密文乘法、加法運算的效率對比，對比結果分別如圖4～圖7所示。從圖中可以看出，GSW方案除了在解密時間上明顯優于本文方案外，在加密、加法運算和乘法運算上操作時間之間差距很小。本方案由于具有訪問控制功能，效率肯定沒有GSW方案高，但可以看出它們之間差距不是很大。

圖2PB-MUFHE加密時間隨訪問策略樹復雜度變化圖

Fig.2Complexity diagram of PB-MUFHE time encryptionwith access policy tree

圖3PB-MUFHE密鑰生成時間隨密鑰中屬性個數變化圖

Fig.3Changes diagram of PB-MUFHE key generation time with the attribute numbers in the key

綜合了以上對本文方案進行的正確性、安全性和操作性能的分析，可以看出本文提出PB-MUFHE方案融合了密文策略-基于屬性加密和全同態加密功能，具有如下特點：

①支持對密文的多次加法和乘法同態運算，且滿足不同用戶之間密文的全同態運算。

②支持對密文細粒度的訪問控制，云端加密數據在未授權情況下，對密文的運算將不滿足同態性。

③滿足多用戶共享。

圖4GSW方案和本文方案加密時間隨參數n的變化圖

Fig.4Encryption time comparison of GSW and PB-MUFHE with parametern

圖5GSW方案和本文方案解密時間隨參數n的變化圖

Fig.5Decryption time comparison of GSW and PB-MUFHE with parametern

圖6GSW方案和本文方案加法運算時間隨參數n的變化圖

Fig.6The addition operation time comparison of GSW and PB-MUFHE with parametern

圖7GSW方案和本文方案乘法運算時間隨參數n的變化圖

Fig.7The multiplication operation time comparison of GSW and PB-MUFHE with parametern

本文結合函數加密和全同態加密機制，構造了一種基于策略的多用戶全同態加密方案(PB-MUFHE)，有效地解決了云環境中的多用戶密文計算、訪問控制、多用戶共享等問題。在安全性方面，PB-MUFHE方案能夠抵制多用戶共謀攻擊，滿足在LWE困難度假設隨機域模型下IND-CPA安全性。在性能方面，PB-MUFHE方案能高效地實現密文數據的全同態運算。下一步工作中，首先考慮給方案加入密鑰撤銷機制，方便有效管理密鑰；其次，使用多線性映射技術取代本方案中的雙線性映射技術，使得方案有更高效的訪問控制；最后將同態自解技術應用到本方案中，提高密文運算次數。

參考文獻:

[1]GENTRY C.A fully homomorphic encryption scheme[D]. San Francisco: Stanford University, 2009.

[2]SMART N P, VERCAUTEREN F.Fully homomorphic encryption with relatively small key and ciphertext sizes[C]//Public Key Cryptography-PKC 2010.Germany:Springer Berlin Heidelberg, 2010:420-443.

[3]STEHLE D, STEINFELD R.Faster fully homomorphic encryption[C]//Advances in Cryptology-ASIACRYPT 2010. Germany:Springer Berlin Heidelberg, 2010:377-394.

[4]GENTRY C, SHAI H.Fully homomorphic encryption without squashing using depth-3 arithmetic circuits[C]//2011 52nd Annual IEEE Symposium on Foundations of Computer Science. Palm Spings, CA: IEEE, 2011:107-116.

[5]GENTRY C, HALEVI S, SMART N P.Better bootstrapping in fully homomorphic encryption[C]// Public Key Cryptography-PKC 2012.Germany:Springer Berlin Heidelberg, 2012:1-16.

[6]GENTRY C, HALEVI S.Implementing gentry’s fully-homomorphic encryption scheme[C]// Advances in Cryptology-EUROCRYPT 2011. Germany:Springer Berlin Heidelberg, 2011:129-148.

[7]SMART N P, VERCAUTEREN F.Fully homomorphic SIMD operations[J]. Designs, Codes and Cryptography, 2012, 71(1): 57-81.

[8]BRAKERSKI Z, VAIKUNTANATHAN V.Efficient fully homomorphic encryption from (standard) LWE[C]// Proceedings of the 52nd Annual Symposium on Foundations of Computer Science.Washington DC: IEEE Computer Society, 2011: 97-106.

[9]BRAKERSKI Z, GENTRY C, VAIKUNTANATHAN V.(Leveled) fully homomorphic encryption without bootstrapping[C]// Proceedings of the 3rd Innovations in Theoretical Computer Science Conference.NewYork: ACM Press, 2012: 309-325.

[10]湯殿華，祝世雄，王林，楊浩淼，范佳.基于RLWE的全同態加密方案[J]. 通信學報，2014，35(1):173-182.

[11]BRAKERSKI Z.Fully homomorphic encryption without modulus switching from classical GapSVP[C]// Advances in Cryptology-CRYPTO 2012.Germany:Springer Berlin Heidelberg, 2012: 868-886.

[12]GENTRY C, SAHAI A, WATERS B.Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based[C]// Advances in Cryptology-CRYPTO 2013.Germany:Springer Berlin Heidelberg, 2013: 75-92.

[13]CLEAR M, MCGOLDRICK C.Policy-based non-interactive outsourcing of computation using multikey FHE and CP-ABE[C]//2013 International Conference on Security and Cryptography.Reykjavik, Iceland:IEEE, 2013:1-9.

[14]CLEAR M, MCGOLDRICK C.Bootstrappable Identity-based fully homomorphic encryption[C]//Cryptology and Network Security. Germany:Springer Berlin Heidelberg, 2014:1-19.

[15]CLEAR M, MCGOLDRICK C.Multi-Identity and Multi-key Leveled FHE from Learning with Errors[C]// Advances in Cryptology -CRYPTO 2015. Germany:Springer Berlin Heidelberg, 2015:630-656.

[16]光焱，祝躍飛，費金龍，顧純祥，鄭永輝.利用容錯學習問題構造基于身份的全同態加密體制[J]. 通信學報，2014，35(2):111-117.

[17]XIAO L L, BASTANI O, YEN I L.An efficient homomorphic encryption protocol for multi-user systems.IACR cryptology ePrint archive[EB/OL]. (2012-01-19)[2016-02-11]. http://eprint.iacr.org/2012/193.

[18]LI T, YE X J, WANG J M.Protecting data confidentiality in cloud systems[C]//The 4th Asia-Pacific Symposium on Internetware (Internetware 2012).New York：ACM Press, 2012:1-12.

(責任編輯梁碧芬)

收稿日期：2015-10-22；

修訂日期：2016-01-14

基金項目：國家自然科學基金資助項目(61363067)；廣西自然科學基金資助項目(2012GXNSFAA053226)

通訊作者：李陶深(1957—)，男，廣西南寧市人，廣西大學教授，博士生導師;E-mail: tshli@gxu.edu.cn。

doi:10.13624/j.cnki.issn.1001-7445.2016.0786

中圖分類號:TP391

文獻標識碼:A

文章編號：1001-7445(2016)03-0786-10

Policy-based multi-user full homomorphic encryption method in cloud computing

LIU Qing1, LI Tao-shen1,2, WANG Ru-wei1,2

(1.School of Computer, Electronics and Information, Guangxi University, Nanning 53004, China;2.Guangxi Colleges and Universities Key Laboratory of Parallel and Distributed Computing,Nanning 530004, China)

Abstract:The full homomorphic encryption technology is an effectively way to solve the problem of cloud computing privacy and security. Considering user diversity in cloud environment, a policy based multi-user full homomorphic encryption scheme (PB-MUFHE) is proposed. On the basis of full homomorphic encryption algorithm, the scheme sets appropriate access policy in the encrypted data and sets the attribute in the key, which is not only to meet full homomorphic operation of the multi-user ciphertext and the multi-user share, but also to support for fine-grained access control Security analysis shows that PB-MUFHE can resist collusion attacks, and is proved IND-CPA security in the random fields model under the LWE harder assumption. Performance assessment demonstrates that PB-MUFHE ciphertext can efficiently implement data fully homomorphy operation and effectively support access control and multi-user shared.

Key words:cloud computing; full homomorphic encryption; multi-user; attribute based encryption; ciphertext policy access control

引文格式： 劉青,李陶深,黃汝維.云計算環境中基于策略的多用戶全同態加密方法[J].廣西大學學報(自然科學版)，2016，41(3)：786-795.