常幅載荷下滑軌與滾輪壽命及可靠性研究

王浩，郭蘭中，林化清,楊蘭玉

(1.中國礦業大學 機電工程學院，江蘇 徐州 221116； 2.常熟理工學院 機械學院，江蘇 蘇州 215500)

飛機襟翼收放系統中，磨損是造成系統機械故障的主要原因[1-2]。滑軌和滾輪是襟翼收放機構的重要運動副，兩者之間的磨損不僅改變各自的尺寸精度，也會改變運動副間的配合尺寸以及配合精度，降低運動精度或者出現動作不協調，嚴重影響飛機的可靠性。當磨損超過一定限度時，就有可能影響襟翼的準確收放，造成兩側襟翼開度不一致或發生機械卡阻，危及飛行安全。因此，研究襟翼收放機構中滑軌與滾輪之間的磨損及其可靠性[3]，對確定其使用壽命，制定檢查周期、大修周期以及維修要求，保證飛行安全具有重要意義。大量的實踐表明，在軸承與滑軌組成的運動副中，軸承的磨損失效是導致整個運動副乃至整個機構的失效的主要原因，因此將以襟翼收放系統中的軸承為中心進行研究。

1 滾動軸承磨損壽命的理論計算

磨損失效指表面之間的相對滑動摩擦導致工作表面金屬不斷磨損而產生失效。持續的磨損將引起軸承零件逐漸損壞，并最終導致軸承尺寸精度喪失及其他相關問題。磨損會影響形狀變化，配合間隙增大及工作表面形貌變化，影響潤滑劑或使其污染達到一定程度造成潤滑功能完全喪失，最終使軸承喪失旋轉精度乃至不能正常運轉。磨損失效是各類軸承常見的失效形式之一。

滾動軸承磨損壽命是指軸承在使用過程中，隨著使用時間的增加，軸承由于過量磨損而喪失正常工作性能的累計總轉數，或在一定轉速下的工作小時數。

由于軸承磨損規律復雜, 磨損壽命尚無完善的計算方法, 通常用徑向游隙的增量來表示軸承的磨損量, 根據許用磨損系數進行估算，最終得到滾動軸承的磨損壽命計算公式為[4,5]

Lw=50(0.61lnλ+0.656)×10fv×60n，

(1)

式中：Lw為軸承磨損壽命；λ為軸承工作時的最小油膜系數；fv為軸承許用磨損系數;V為軸承的許用徑向游隙增量;e0為磨損率；n為軸承轉速。

2 滾動軸承磨損壽命的點估計

實踐表明，大量機械設備中傳動系統的失效大部分是由于滾動軸承疲勞磨損而引起的。大量試驗和分析證明，壽命服從正態分布。已知分布形式，即可從樣本出發，求出未知參數的估計。

參數估計可分為點估計和區間估計，現采用點估計，即總體ξ分布的形式已知，分布參數θ1，θ2，…，θm(如正態分布的均值和標準差)未知，從樣本(X1，X2，…，Xn)出發，求出m個統計量，作為未知參數θ1，θ2，…，θm的估計[6]。

正態分布均值的點估計為

(2)

標準差的點估計為

(3)

在指定可靠度R下，可靠壽命的點估計為

(4)

式中：ZR按可靠度R查表1確定。

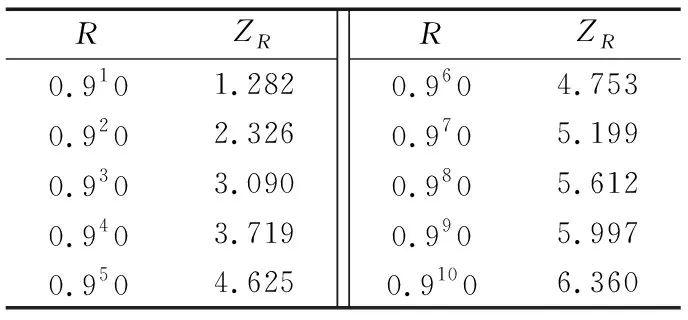
表1 ZR與可靠度R的關系[8]

3 試驗

3.1 試驗設備及試樣

試驗設備為自制的往復式多用途摩擦磨損試驗機,示意圖如圖1所示。整個裝置固定在立柱、壓梁和平臺組成的承力框架中，通過絲杠和壓力傳感器給固定摩擦副的上磨板和車式下磨板施加徑向載荷Fr，聯體式電磁可調電動機通過連桿機構使下磨板做往復運動。該試驗機可一次同時安裝4套軸承及2個與之配對的滑軌(圖2)，不僅可以提高試驗效率，也可保證試驗條件的一致性，從而有效地減小試驗誤差，提高試驗數據的可靠性。

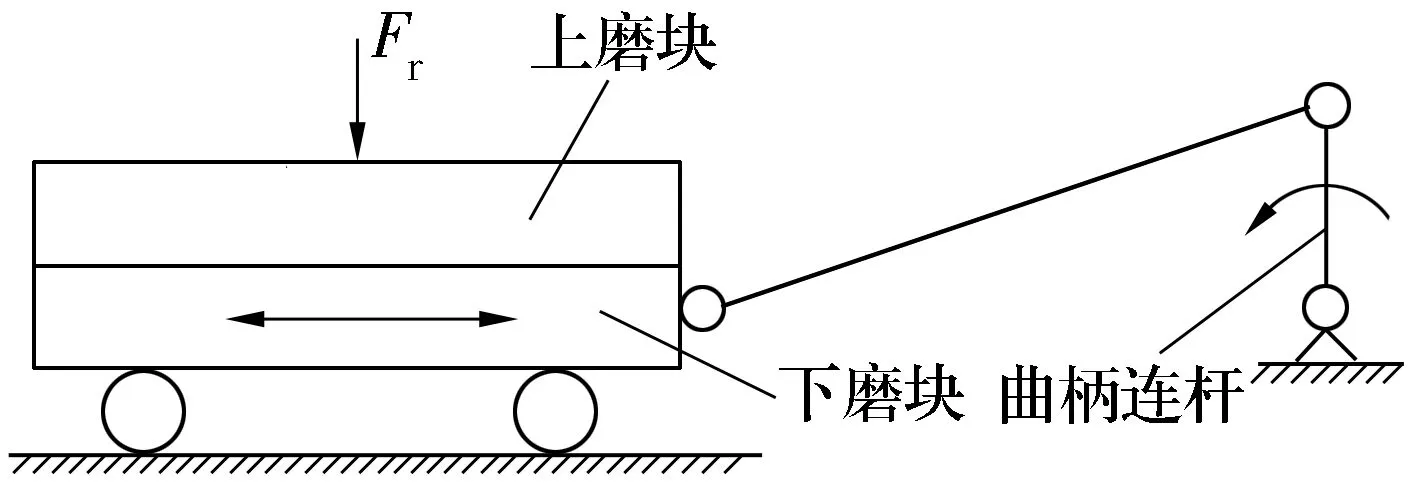
圖1 試驗設備原理圖

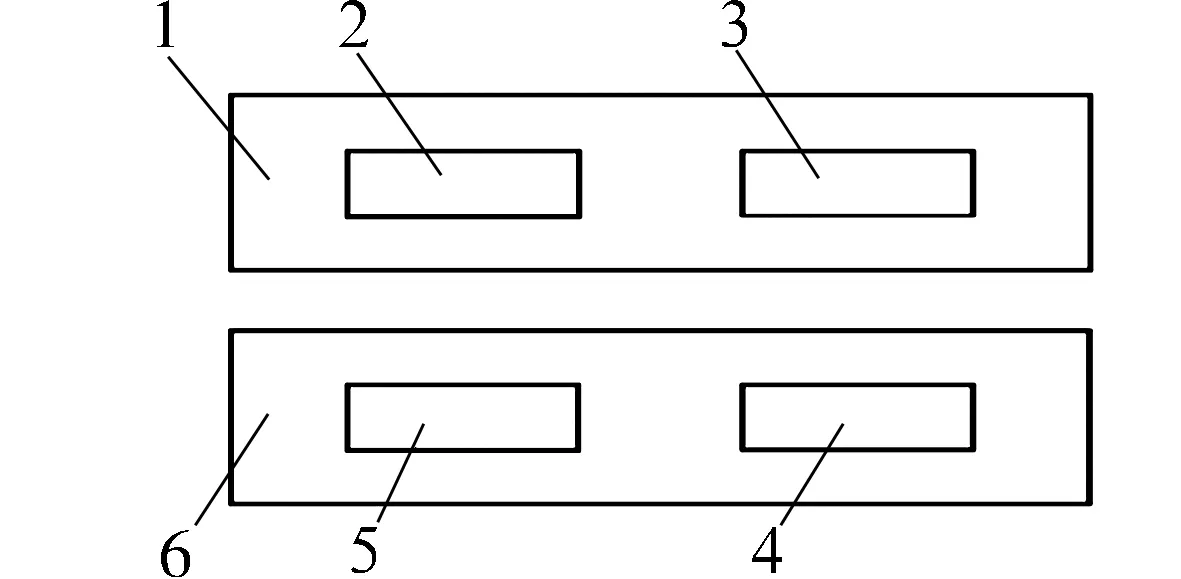
1—滑軌1；2—軸承1；3—軸承2；4—軸承4；5—軸承3；6—滑軌2

為使試驗結果盡可能符合實際情況，上磨塊為36102軸承，材料為GCr15，寬度B=9 mm，內徑d=15 mm，外徑D=32 mm，接觸角α=15°，額定動載荷Cr=4.5 kN。下磨塊(滑軌)材料為40CrNiMoA，結構尺寸如圖3所示。

圖3 下磨塊結構尺寸圖

3.2 試驗方法

文獻[8-9]在進行壽命試驗時，觀察到存在不失效壽命。所以，考慮到滾動軸承在試驗中可能出現無限壽命的情況，即存在一個極限載荷，低于該載荷，軸承便不會產生疲勞破壞，滾動疲勞磨損試驗設計為常幅定數截尾試驗，即當4套滾動軸承試樣中有3套失效即停止試驗。試驗示意圖如圖4所示。

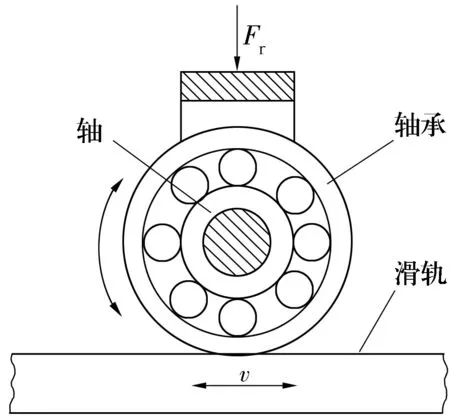
圖4 試驗示意圖Fig.4 Diagram of test

試驗時，加載裝置通過上磨板施加4 000 N的徑向載荷，由于結構尺寸的對稱性，每套軸承承受1 000 N的徑向載荷。載荷通過壓力傳感器以及與其相連接的標準載荷測量儀(準確度<0.005%FS，溫度系數<5×106，A/D轉換速率>50次/s)控制。通過聯體式電磁可調電動機控制轉速，調速范圍為200～1 400 r/min，轉速比i=80，輸出的轉速為2.5～17.5 r/min，試驗時轉速為7 r/min。試驗部件的力學性能見表2。

表2 部件材料的力學性能

軸承失效的判定：在試驗過程中，當軸承出現旋轉精度降低，最終無法正常工作時，視為該軸承磨損失效。

采用外圓千分尺測量軸承的磨損量，即為原始尺寸與相互垂直的2個直徑方向上測量值的平均值之差；采用深度千分尺測量滑軌的磨損量，取整個磨損表面均勻分布的9個測點測量值的平均值。

3.3 結果與分析

軸承失效時的循環次數見表3，其磨損量與壽命曲線如圖5所示。由于試驗機一次循環軸承滾動距離為520 mm，而軸承外徑為32 mm，通過計算可得，一個循環即曲柄旋轉一周，軸承轉數為5.18 r。滑軌的磨損量與壽命曲線如圖6所示。軸承和滑軌平均磨損量對比如圖7所示。

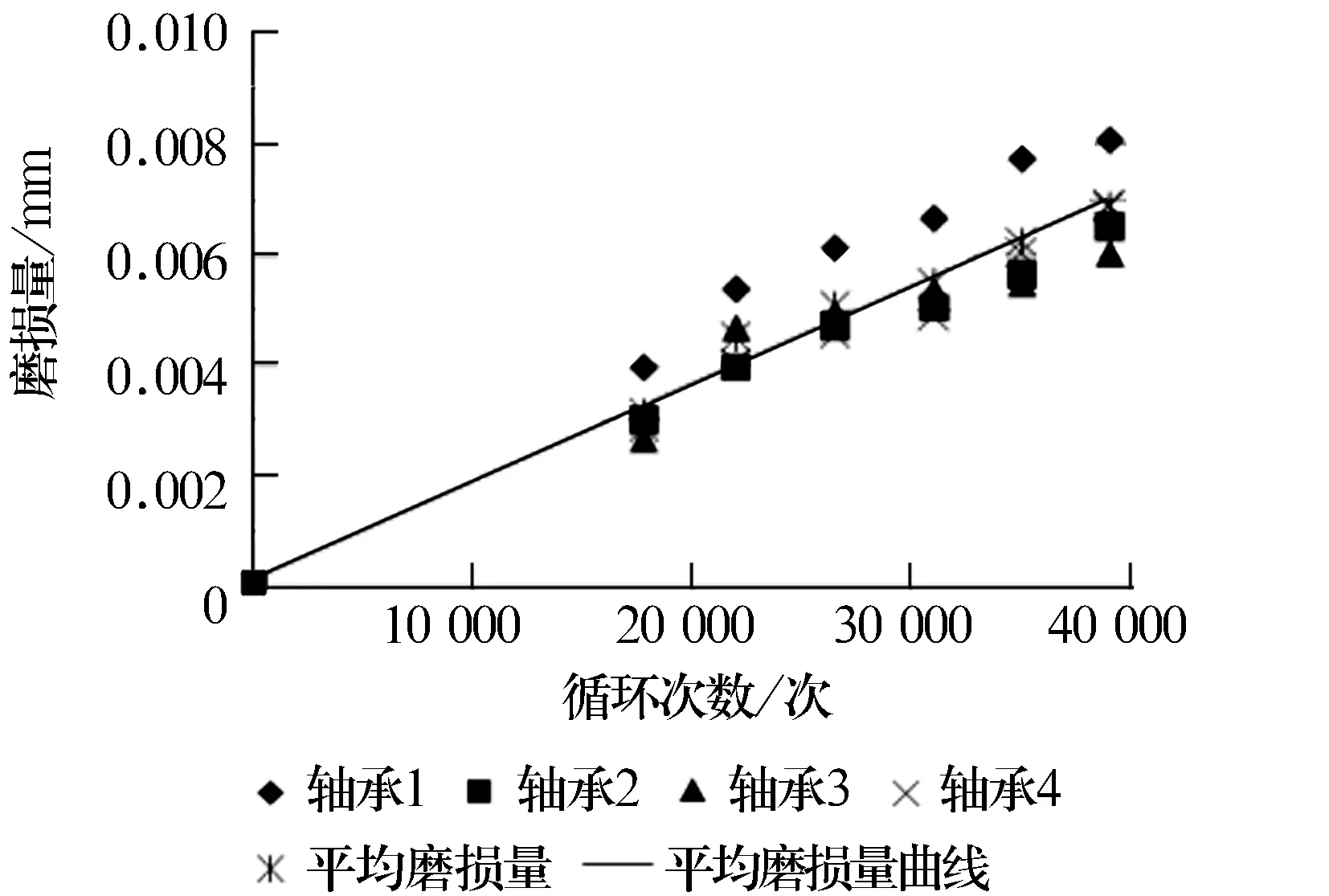
圖5 軸承磨損量與壽命曲線

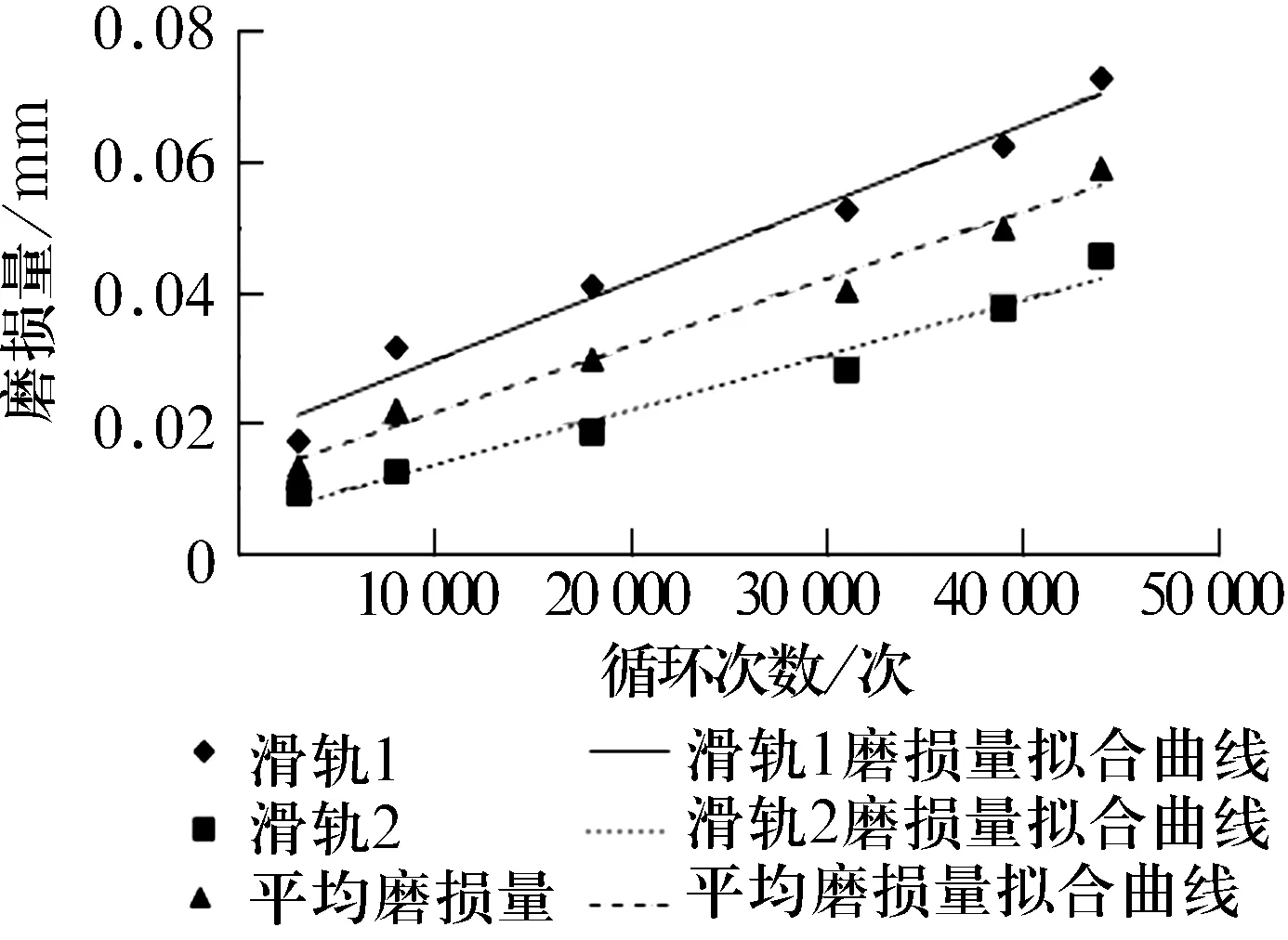
圖6 滑軌磨損量與壽命曲線

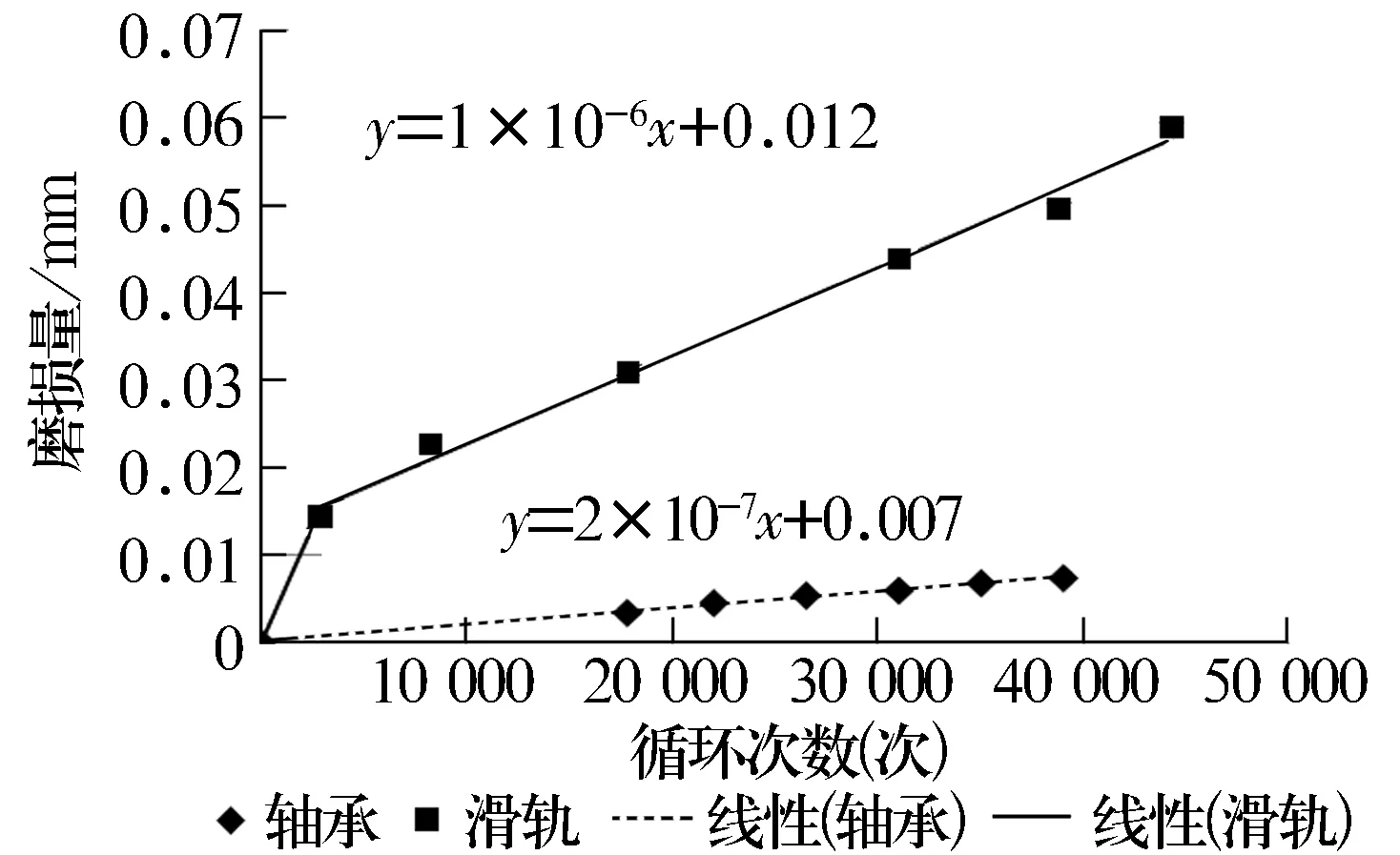
圖7 軸承與滑軌平均磨損量對比

由表3可知，當循環次數達到43 965次(軸承轉數為227 739 r)時，有3套軸承失效。因此可初步認為，在相同工作條件下，36102軸承的可靠工作壽命不會超過227 739 r。

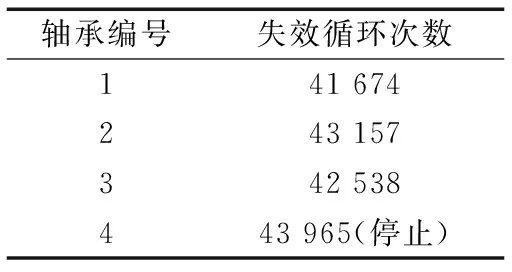
表3 滾動軸承失效時的循環次數

由圖5和圖7可知，軸承磨損量擬合曲線的左端延長線距離坐標原點很近，說明該軸承在投入工作后，基本沒有磨合期，一開始就處于比較穩定的磨損狀態，且磨損量的擬合曲線斜率很小，表明在相同循環次數下增加的磨損量比滑軌小。這是由于航空滾動軸承的尺寸精度、形狀精度和表面質量均較高。

由圖6和圖7可知，滑軌存在比較明顯的磨合期，范圍大致在3 000次循環，此時磨損量達到0.015 mm，然后穩定增加，但磨損量擬合曲線初始階段斜率較大，表明在相同循環次數下增加的磨損量比滾動軸承大。

由此可知，在滾動軸承與滑軌組成的摩擦副中，滑軌磨損量比軸承大。

4 滾動軸承理論磨損壽命和試驗壽命對比分析

已知：根據軸承的應用經驗,將該軸承的許用徑向游隙增量定為徑向游隙的20%，該軸承接觸角為15°,徑向游隙為13.9 μm,即增量V為2.78 μm，磨損率e0取為1.2 μm，這樣該軸承許用磨損系數fv取值約2.316 ,又經計算,軸承工作時最小油膜系數λ=6.77,代入(1)式可得軸承壽命Lw=5.05×106r。

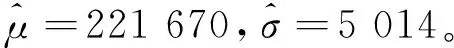
比較軸承理論壽命(5.05×106r)和根據試驗數據計算的壽命點估計(2.10×105r)可知，前者是后者的24倍。軸承壽命非常離散，一批結構、材料、熱處理、加工方法均相同的軸承在相同工況下，其最高和最低壽命有可能相差幾十倍甚至更多[4,10]，原因為：

1)滾動軸承磨損壽命計算方程都是建立在大量試驗基礎上的。試驗時軸承內圈相對于軸、外圈相對于軸承座無相對運動，僅內、外圈之間通過鋼球發生相對運動，且通過潤滑系統進行潤滑[11]，并通過調整潤滑油流速控制試驗溫度。而本試驗在室溫下進行，除了內、外圈的相對運動以外，外圈對于滑軌有相對運動，且采用油脂潤滑，無法對試驗溫度進行嚴格控制，運動形式和工作環境較為復雜。

2)在滾動軸承磨損壽命計算方程中，V,e0,fv,λ對計算結果影響大。在計算過程中，λ與e0可以通過一定的估算得到，而徑向游隙的增量V則定為徑向游隙的20%，該值是根據應用經驗得出，可能存在一定的誤差。若要使滾動軸承磨損壽命計算方程的計算結果與實際相吻合，可對V,λ,e0的取值問題進行更進一步的深入研究，并給出具有可操作性的取值原則。

由于影響滾動軸承壽命的因素復雜，磨損壽命理論仍需進一步完善。本試驗屬于模擬臺架試驗，由于樣本較少，基于正態分布的可靠壽命點估計的誤差不容忽視，但4套軸承中有3套均在2×105r以后失效，可以認為通過試驗確定的壽命的點估計是可信的，同時也說明理論計算公式還存在一定缺陷。

5 結束語

通過試驗研究了常幅載荷下滾動軸承與滑軌的疲勞磨損行為，并采用滾動軸承磨損壽命計算方程計算其理論壽命，同時根據試驗數據，對給定可靠度為0.99時的軸承壽命進行了估計。由試驗結果可知，高精度滾動軸承磨損量基本隨時間呈線性關系，沒有明顯的磨合階段；而滑軌則存在明顯磨合階段。這是由二者精度和表面質量不同所致。軸承理論壽命和根據試驗數據計算的壽命的點估計存在較大差異，這是由系數V,λ,e0取值的模糊性造成的。