面向裝配系統可靠性分析的車身夾具系統優化設計

劉銀華　紀飛翔　葉夏亮

上海理工大學，上海，200093

?

面向裝配系統可靠性分析的車身夾具系統優化設計

劉銀華紀飛翔葉夏亮

上海理工大學，上海，200093

摘要：為描述多工位車身裝配系統的漸進衰退特性，建立了面向車身產品尺寸質量和夾具系統要素的裝配系統可靠性模型。結合夾具設計穩定性參數約束，提出了面向白車身裝配系統可靠性的車身多工位焊裝過程的夾具布局優化方法；在給定夾具布局下構建了定位銷制造成本函數，提出多工位夾具定位銷磨損率的優化模型并對其進行優化分配。將上述方法應用于側圍裝配案例，分析發現優化后裝配系統可靠性衰退過程得到較大改善，并有效提升了夾具系統的使用壽命。

關鍵詞：車身裝配；尺寸質量；可靠性模型；夾具布局；磨損率

0引言

汽車、飛機、船舶這類產品均由大量薄板件焊裝制造而成，其尺寸質量對產品的使用性能、可靠性、強度以及安全性等均有重要影響。在薄板件焊裝過程中，產品尺寸質量受到來料零件偏差、夾具系統狀態以及焊接等多因素影響，其中夾具系統是影響產品尺寸質量的最關鍵因素。在夾具布局的方案設計方面，許多學者進行了深入的研究。Chou等[1]基于螺旋理論分析了夾具的完全約束問題；Lakshminarayana[2]基于形閉合和力閉合的力學分析從靜態平衡的角度利用代數理論對定位元件布局點的個數進行了分析；Menassa等[3]通過有限元建模來確定定位點的位置，保證工件在主要定位表面的法向變形最小。謝偉松等[4]通過蟻群算法等來優化多階段裝配過程中的夾具布局；鄭軍紅等[5]基于神經網絡和遺傳算法進行了夾具的智能規劃。

上述方法均是面向產品質量的夾具定位方案靜態設計，沒有考慮裝配過程中定位元件磨損等動態因素，無法基于裝配系統可靠性衰退過程來約束定位元件的布局。夾具定位元件在薄板件定位、裝卸等長期使用過程中會持續磨損，研究發現，不同材料、制造工藝下定位元件定位性能衰退對裝配系統可靠性的影響是不同的[6]，然而在傳統夾具系統制造中，同功能的定位元件材料和鍍層等工藝均是相同的。因此如何針對夾具布局方案和定位元件磨損率參數進行全面的優化設計是保證裝配系統可靠性的關鍵。本文提出基于裝配系統可靠性評估的夾具系統優化方法，用來提升裝配系統的可靠性和車身產品質量。

1車身裝配系統可靠性評估模型

在車身產品裝配過程中，72%的尺寸質量問題由夾具相關的因素引起[7]，車身夾具系統狀態是決定車身產品尺寸質量的最重要因素之一。傳統夾具系統可靠性模型主要考慮夾具系統失效概率，無法對裝配產品的質量信息進行有效表達。本文主要考慮夾具系統、來料零件等因素對產品質量的影響和夾具系統在長期定位使用中自身的磨損對其定位能力的影響，將車身多工位裝配系統的可靠性定義為在給定的焊裝時間內夾具系統要素運行良好并且生產出合格產品的概率。可見車身多工位裝配系統失效由兩方面原因導致：一是焊裝系統要素失效；二是在當前焊裝要素衰退狀態下生產的產品尺寸質量不合格。根據劉銀華等[8]的研究，裝配系統可靠性由焊裝系統要素可靠性和裝配產品質量可靠性兩部分組成，則白車身多工位焊裝系統可靠性為

R(t)=Rf(t)·Rq(t)=

(1)

式中，R(t)為t時刻的白車身多工位焊裝系統可靠性；Rf(t)為t時刻的白車身多工位焊裝系統要素可靠性；i為第i個定位銷；α為夾具系統中定位銷的數目；Rq(t)為白車身產品質量可靠性；βu為某關鍵產品特征(KPC)的偏差量，可通過狀態空間法算出；X為當前夾具系統要素狀態，即定位元件的磨損狀態；u為測點數目,u=1,2,…,n，若考慮給定測點在薄板件平面內的裝配偏差，則其平面內兩個方向的偏差均為關鍵產品特征；var(·)為方差函數；ηu為給定的偏差的方差閾值。

以下將以裝配系統可靠性指標作為目標函數，對多工位的夾具布局方案進行優化設計。

2多工位夾具系統的優化設計

裝配系統可靠性模型包含了夾具布局位置以及產品質量等多因素及其相關變量，本節將基于該可靠性模型對多工位夾具系統布局和定位銷磨損率參數進行優化設計，以獲得更穩健的夾具系統方案，保證白車身產品質量。

2.1夾具布局設計

2.1.1薄板件定位幾何模型與穩定性參數約束

對于薄板件的定位，工程中實際應用的定位方式為N-2-1定位，當薄板件剛性較大時N取3，其定位模型如圖1所示。Cai等[9]給出了夾具布局的雅可比矩陣J，該矩陣的秩等于薄板件被夾具所約束自由度的數目，因此一個能完全約束薄板件自由度的夾具布局方案的雅可比矩陣的秩等于6。

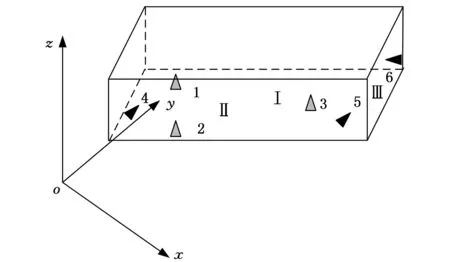
圖1　薄板件3-2-1定位方案模型

采用圖1中夾具定位方案時，由于夾具在焊裝過程中的磨損會導致定位誤差，即夾具系統性能衰退，所以該工位的裝配產品也會相應產生尺寸偏差。兩者之間的關系用下式描述：

Δq=JΔd

(2)

式中，Δq為產品尺寸偏差；Δd為夾具布局處在薄板件表面法線方向主要由于磨損導致的定位偏差。

薄板件被夾具完全約束的空間穩定性稱為該定位方案的幾何穩定性，即在該定位方案下的產品尺寸偏差對夾具偏差的不敏感性。Xiong等[10]在上述雅可比矩陣的基礎上，給出了穩定性參數φ的計算方法，用來衡量夾具布局穩定性的好壞，其表達形式如下：

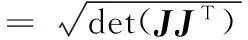
(3)

其中，det(JJT)為求JJT的行列式。當雅可比矩陣可逆時φ=‖J‖。

根據給出的雅可比矩陣表達形式，可以得到圖1中薄板件在圖示定位方案下的穩定性參數：

φ=‖J‖=8|(x2y3+x3y1+x1y2-x2y1-

x1y3-x3y2)(y5-y4)|=18EL

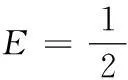
L=|y5-y4|

其中，xi、yi為圖1中各定位點的位置坐標。

通過轉化可知E為Ⅰ面上3個定位塊(即1，2，3)圍成的面積，L為Ⅱ面上2個定位點(即4，5)之間的距離。據此在穩定性參數的約束下，Ⅰ面上3個定位塊圍成的面積越大，Ⅱ面上2個定位點之間的距離越遠，其夾具布局穩定性越好。

2.1.2面向系統可靠性的夾具布局優化

在薄板件定位中，其穩定性參數達到極值時夾具布局方案并不是唯一的。因為焊裝過程中薄板件板面方向的尺寸偏差主要由2個定位銷定位布局來控制，而3個定位塊主要控制薄板件垂直于板面方向的尺寸偏差，由此，在研究板面方向的尺寸偏差時不考慮3個定位塊對其影響。當給定3個定位塊的面積時，圖2中的3種布局方案下的穩定性參數值是相同的，但是這3種布局方案下系統可靠性衰退過程是不同的[8]。因此以下將基于穩定性參數的約束，結合裝配系統可靠性對夾具布局進行優化。

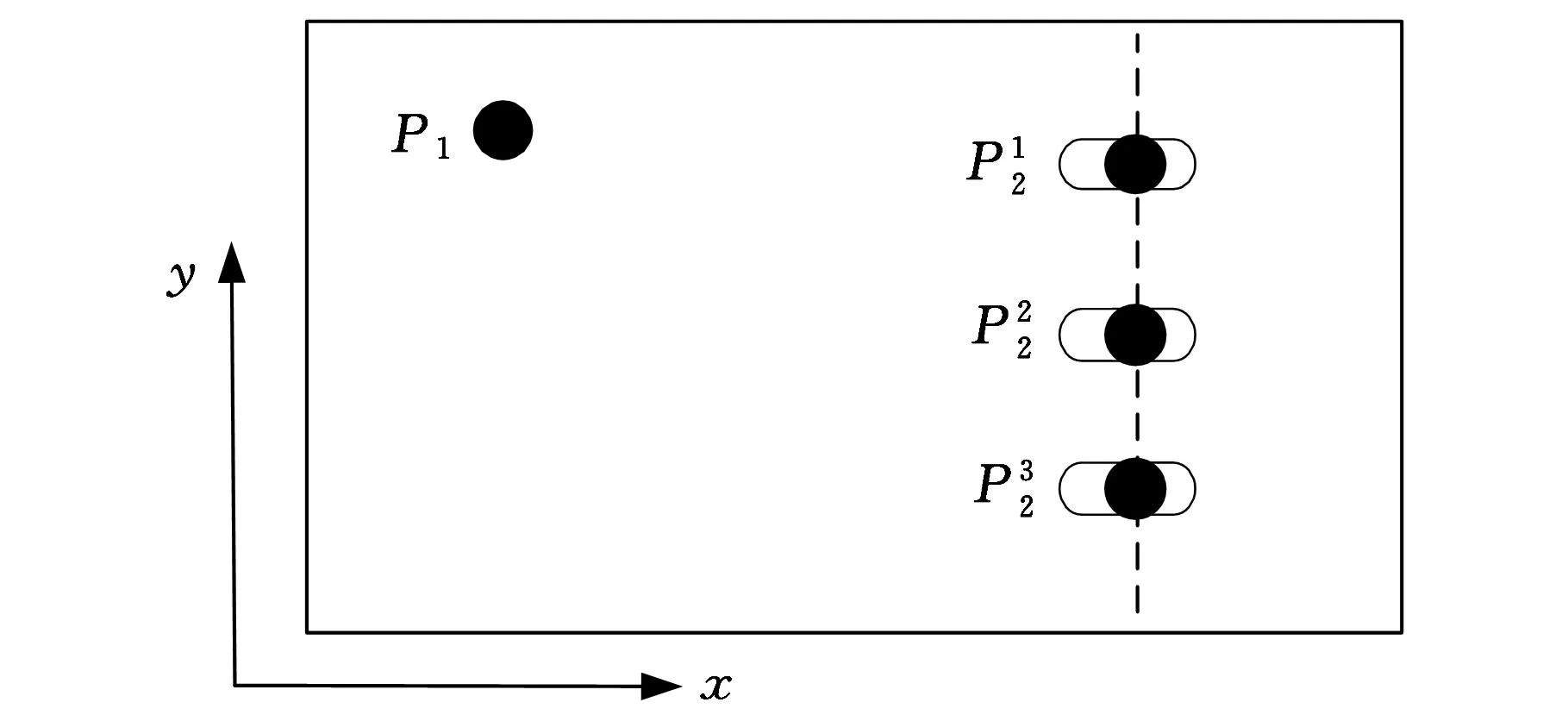
圖2　穩定性參數相等的三種夾具布局方案

首先對薄板件進行網格劃分，網格交叉點為候選夾具定位點，獲得初始的夾具布局方案集；然后基于穩定性參數最大化原則，即最大化Ⅱ面上2個定位點上的距離得到縮減后的夾具方案集；進一步針對不同的夾具方案，在MATLAB軟件中采用MonteCarlo仿真，獲得相應裝配次數下的系統可靠性曲線。通過設定可靠性閾值，獲得系統可靠性衰退到所設定閾值時裝配系統對應的裝配次數，如果存在唯一的最大裝配次數值，則對應夾具布局方案為最優夾具布局。如果最大裝配次數值非唯一，可通過對不同夾具布局方案下的產品尺寸波動水平進行計算對比，從而優選出相應的夾具方案。總體尺寸質量指標可表示為

(4)

其中，σi為KPC尺寸偏差的均方差；R*為系統可靠性閾值；6σR*為可靠性指標達到閾值時產品的總體尺寸質量指標；j為工位指標。6σR*(j)反映了j工位上產品總體尺寸質量，如果j取最終工位，那么就表示最終工位產品總體尺寸質量。由于在其他條件一定時最終產品總體尺寸質量和定位元件布局方案之間是一一對應的，因此可以獲得唯一最優的夾具布局方案。整個夾具布局方案確定步驟如下：

(1)對薄板件進行網格劃分，網格交叉點為備選夾具定位點，根據這些備選點統計出所有可能的布局方案，進入步驟(2)。

(2)在工裝夾具允許的安裝位置下，結合雅可比矩陣和夾具設計穩定性參數對夾具布局進行約束，得到縮減的夾具布局方案集合，進入步驟(3)。

(3)計算步驟(2)中各夾具布局方案下裝配系統可靠性達到可靠性閾值時的裝配操作次數，如果找到最大裝配次數的唯一方案，即為最優夾具布局方案，否則進入步驟(4)。

(4)計算步驟(3)中得到的夾具布局方案集在系統可靠性閾值下的產品總體尺寸質量指標6σR*(j)，該指標最小的布局方案為最優方案。

2.2定位銷磨損率優化

在定位銷的裝卸過程中，當給定裝配次數時其磨損率是一隨機變量，本文用平均磨損率μΔ來表示一定裝配次數下的定位銷磨損率。定位銷磨損率除了和裝配次數有關外，主要由定位銷材料和制造工藝決定，即主要由定位銷的制造成本決定。從制造可行性和經濟性方面考慮，制造成本在其最小和最大成本之間取值，同時定位銷的磨損率和制造成本相關且成反比，則磨損率μΔ和制造成本Cp的關系可表示為

(5)

式中，κ為修正系數，其值的大小和平均磨損率所屬的區間有關。

裝配過程中KPC偏差的波動水平對焊裝系統中每一個定位銷磨損量的敏感度不同，不同的敏感度反映了各個定位銷磨損量對產品總體尺寸質量的影響。根據這種敏感度來分配對應夾具的制造成本，對于敏感度大的定位銷，其定位性能衰退對產品總體尺寸質量影響較大，應該分配較高的制造成本，使其磨損率較小；反之，敏感度小的定位銷應該分配較低的制造成本。設焊裝系統定位銷的總制造成本為C0，則定位銷磨損優化模型可以表示為

(6)

式中，μΔmax、μΔmin為磨損率上下限。

針對該優化模型的求解可通過MATLAB軟件中函數fmincon進行計算，即獲得固定成本約束下的磨損率參數的優化結果。

3案例

圖3為某汽車側圍的2D焊裝流程圖，前三個工位薄板件以搭接的形式進行焊裝，焊裝后該分總成在第4個工位對其測點進行尺寸質量檢測。表1所示為檢測工位測點的坐標，表2所示為各工位在夾具設計穩定性參數約束下的可行夾具定位點集，通過分析可見該點集共有16種夾具布局方案。

設白車身裝配系統可靠性閾值為0.7，按照給出的白車身焊裝系統可靠性評估模型，利用表3給出的參數計算由穩定性參數約束下得到的16種夾具布局方案達到系統可靠性閾值時系統運行的次數，如圖4所示。由圖4可知，在16種夾具布局方案中，方案1、方案6、方案13是最優的三種方案，對比這三種布局下產品總體尺寸質量指標6σ0.7(4)，由此確定方案6為最優方案，該方案的定位點坐標見表4。

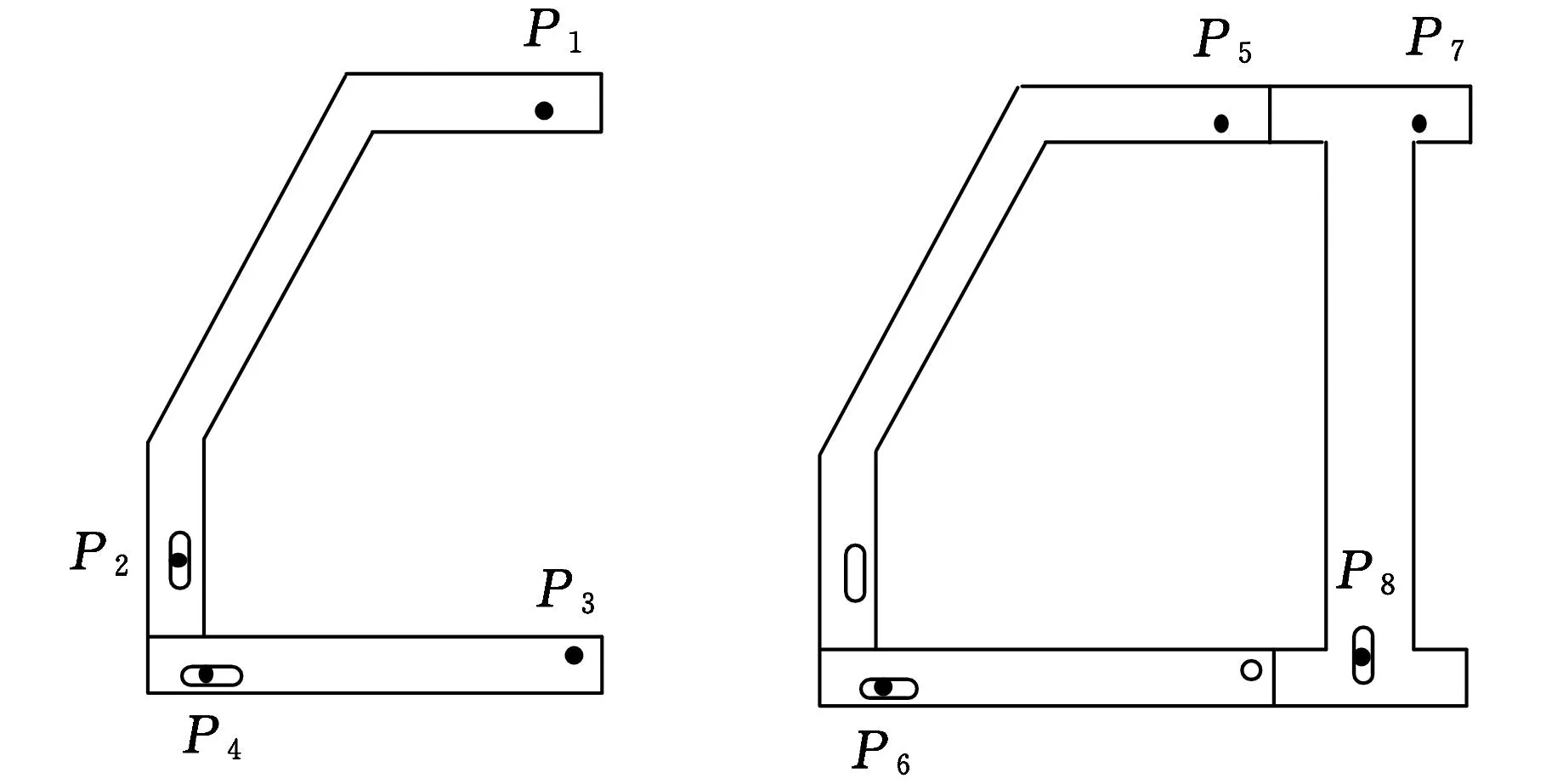
(a)工位1(b)工位2

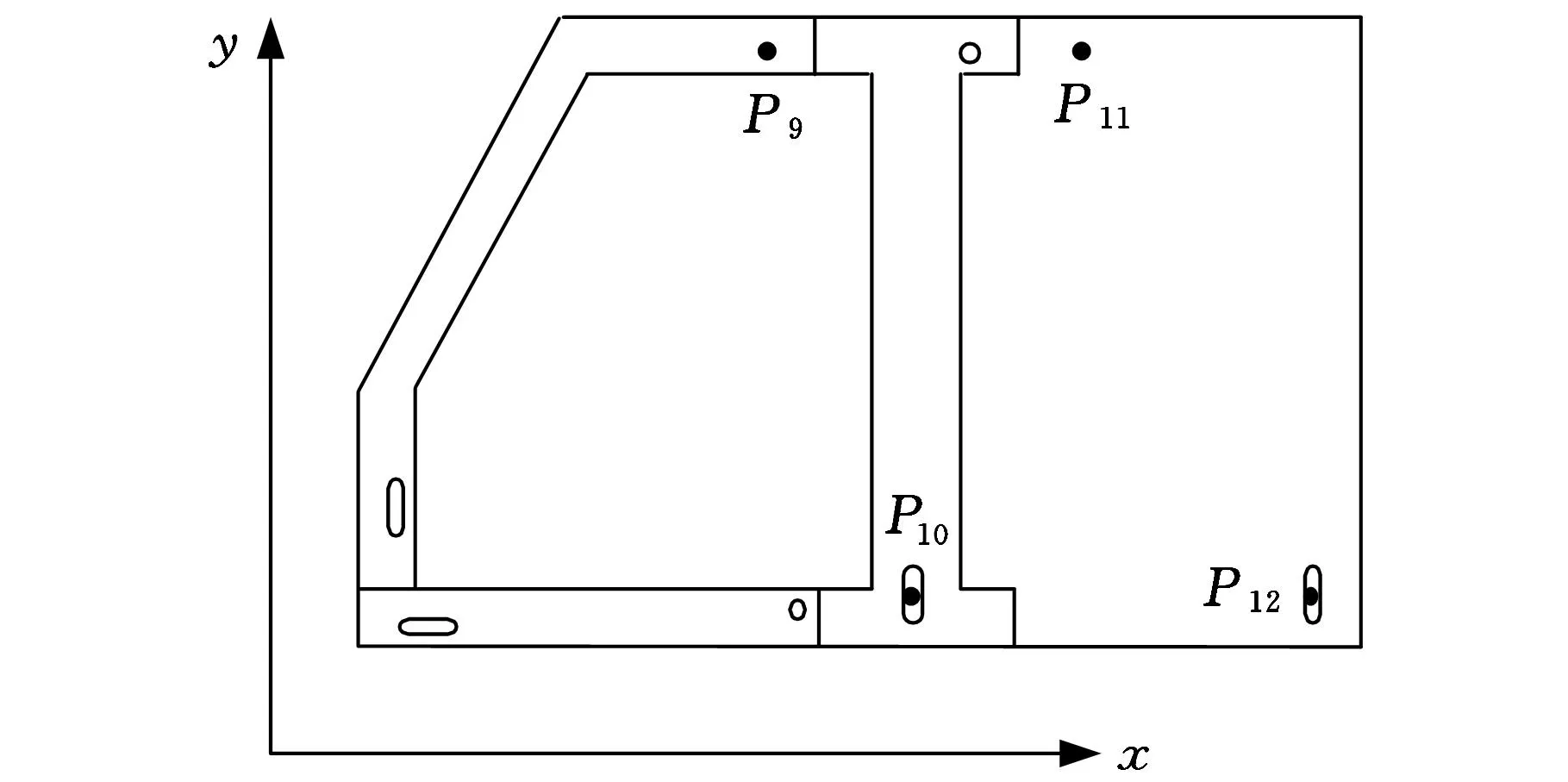
(c)工位3

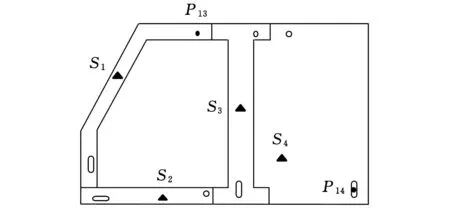
(d)工位4圖3　焊裝工位流程

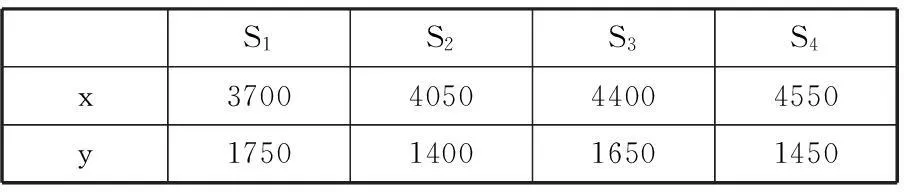
表1　測點坐標值　mm

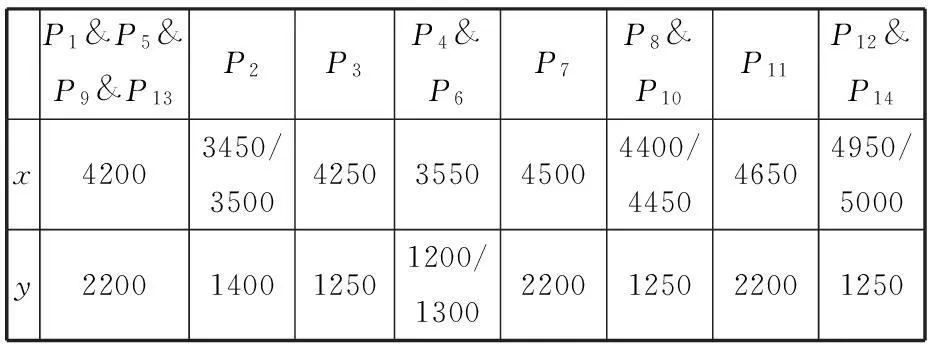
表2　夾具穩定性參數約束下的夾具布局方案　mm

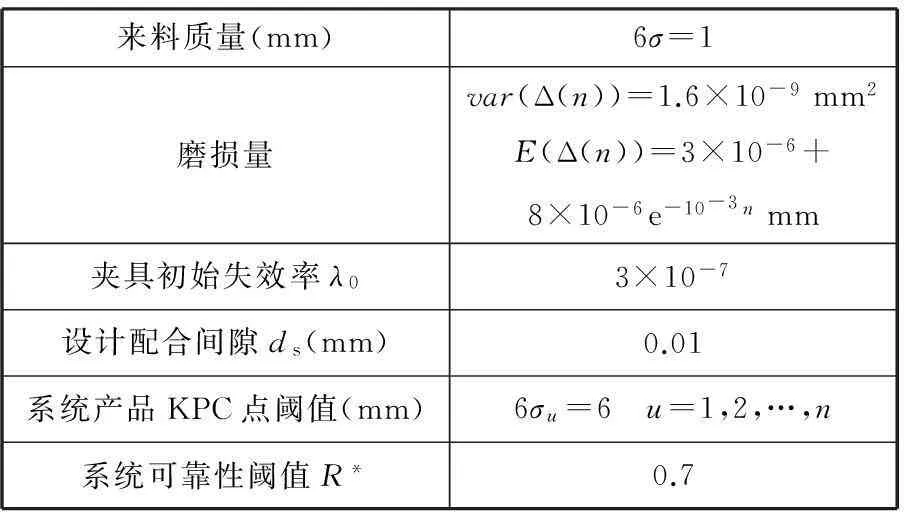
表3　系統可靠性計算參數設定表

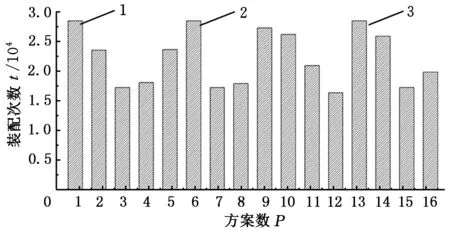
1.6σ0.7(4)=11.84 mm　2.6σ0.7(4)=11.51 mm3.6σ0.7(4)=11.99 mm圖4　各定位方案下系統失效時的裝配次數

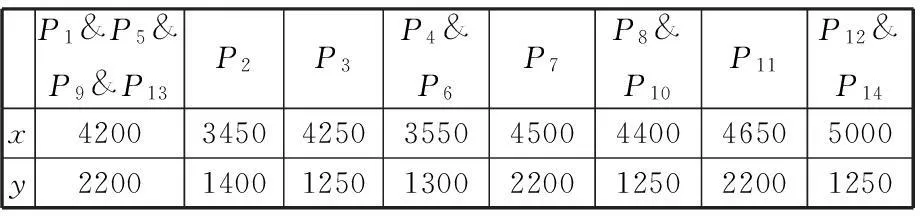
mm

在該最優方案下，各定位銷磨損對工位4上的總體尺寸質量指標6σ0.7(4)的敏感度系數見表5。

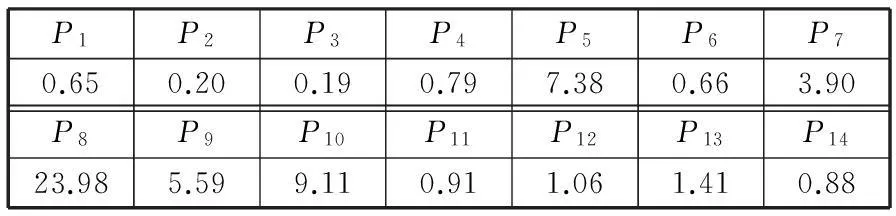
表5　最優方案下各定位銷磨損對產品質量的敏感度系數

根據Jin等[11]給出的定位銷磨損分布函數，過了磨合期之后定位銷磨損率收斂于3×10-6mm。設在能接受的制造成本下磨損率下限為μΔmin=1×10-6mm，上限為μΔmax=6×10-6mm，且在該區間下κ為定值，則總制造成本為

根據式(6)的優化模型得到3個裝配工位各定位銷的磨損率如表6所示。從表中可見優化后多個定位銷的磨損率是相同的，這是因為總體尺寸質量指標對這些定位銷的磨損狀況敏感度較低，導致其優化后應分配到的制造成本較低，對應的定位銷的磨損率超出了實際中能接受的定位銷磨損率區間，因此對于這類定位銷的磨損率取相應區間極大值。

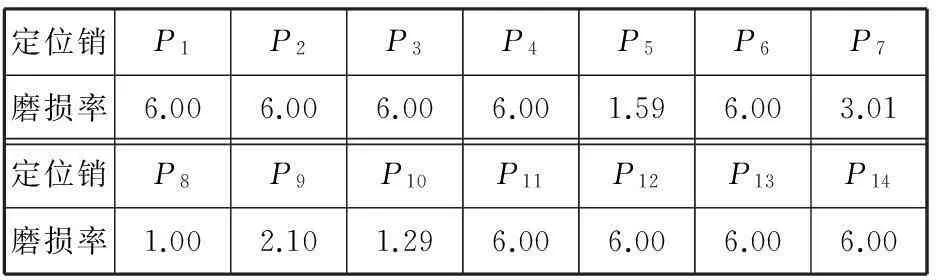
表6　優化后定位銷磨損率　nm

通過MATLAB軟件分別基于定位銷磨損率優化分配前后的磨損率分配值來編寫系統可靠性Monte Carlo仿真代碼，得到對應裝配次數下的系統可靠性值，如圖5所示。圖5表示定位銷磨損率優化前后系統可靠性衰退過程，通過對比可見：磨損率優化前系統運行到約23 000次時系統可靠性急劇下降，在運行到約36 000次時系統完全失效；定位銷磨損率優化后系統運行到約42 000次之前系統可靠性都是平緩下降的，在這之后開始急劇下降，運行到約55 000次時系統完全失效。由此可見，在同樣的夾具制造成本下，通過合理分配定位銷的制造成本(即定位銷的磨損率參數)，焊裝系統的壽命明顯提升。

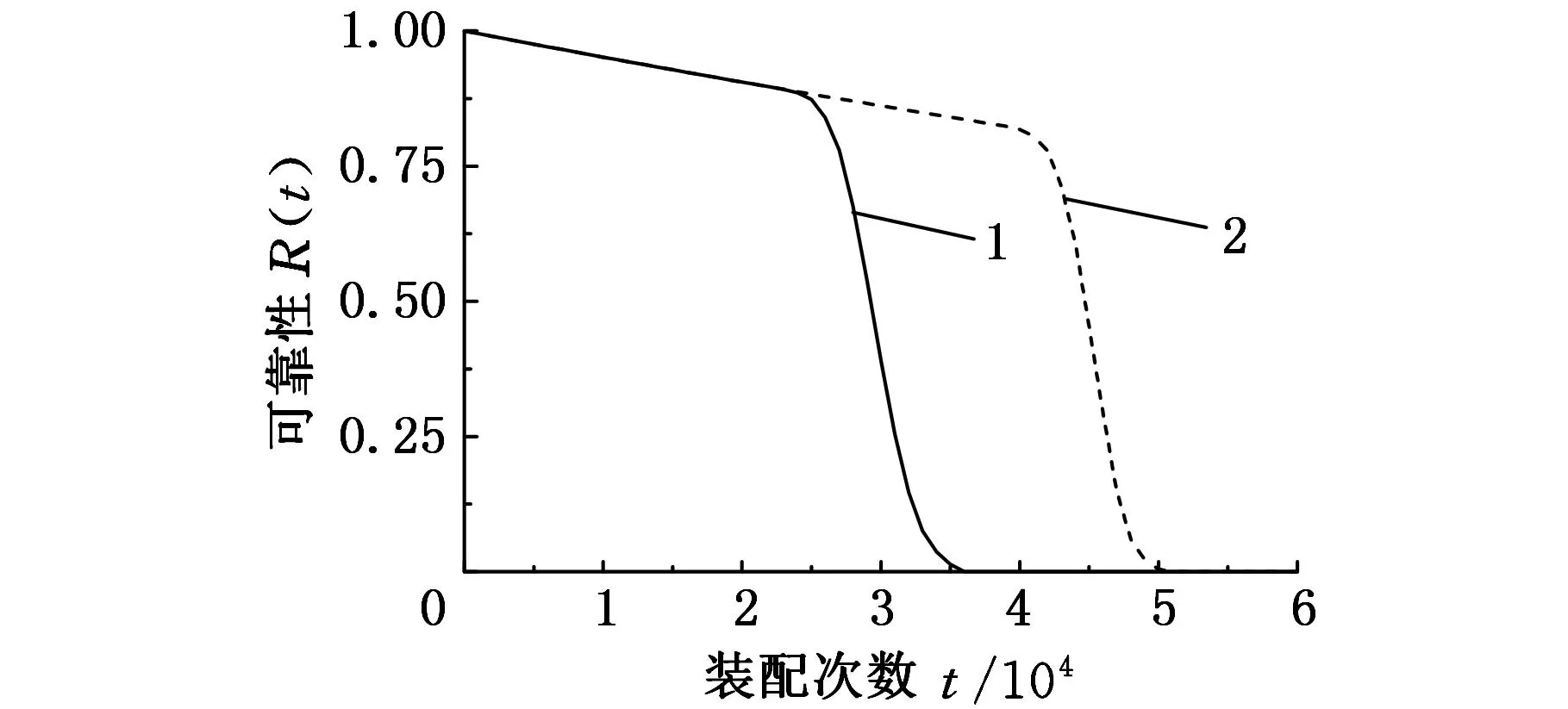
1.優化前　2.優化后圖5　優化前后裝配系統可靠性衰退曲線

4結束語

本文提出了基于裝配系統可靠性評估的夾具系統優化方法。通過研究夾具系統要素可靠性和產品質量可靠性的評價方法，建立了集成多因素的白車身裝配系統可靠性評估模型。結合夾具設計穩定性參數約束對夾具布局方案進行了優選。進一步通過對夾具系統制造成本和定位銷磨損率參數的關系模型構建，在夾具制造成本約束下對定位銷磨損率參數進行了優化分配，對比優化前后焊裝系統可靠性衰退過程，發現優化后焊裝系統的衰退得到了有效的改善，顯著提升了焊裝系統的使用壽命。

參考文獻：

[1]Chou Y C, Chandru V, Barash M M.A Mathematical Approach to Automatic Configuration of Machining Fixtures: Analysis and Synthesis[J]. ASME Journal of Engineering for Industry， 1989,111(4):299-306.

[2]Lakshminarayana K. Mechanics of Form Closure[J]. Acta Mechanica, 1984,52(1):107-118.

[3]Menassa R J, DeVries W R. Optimization Methods Applied to Selecting Support Positions in Fixture Design[J]. ASME Journal of Engineering for Industry, 1991,113(4):412-418.

[4]謝偉松，鄧錚，丁伯慧.用 CAAA 優化多階段裝配過程中的夾具布局[J].中國機械工程，2015,26(5)：658-663.

Xie Weisong, Deng Zheng, Ding Bohui. Fixture Layout Optimization in Multi-station Assembly Process Using GAAA[J]. China Mechanical Engineering, 2015，26(5)：658-663.

[5]鄭軍紅，葉修梓，陳志楊. 基于神經網絡和遺傳算法的智能夾具規劃[J].中國機械工程, 2008，19(19): 2376-2381.

Zheng Junhong, Ye Xiuzi, Chen Zhiyang. Intelligent Fixture Planning Based on Artificial Neural Network and Genetic Algorithms[J]. China Mechanical Engineering, 2008,19(19): 2376-2381.

[6]Chen Y, Jin J, Shi J. Integration of Dimensional Quality and Locator Reliability in Design and Evaluation of Multi-station Body-in-white Assembly Processes[J]. IIE Transactions, 2004, 36(9):827-839.

[7]Ceglarek D,Shi J I, Zhou Z. Variation Reduction for Assembly: Methodologies and Case Studies Analysis[R]. Ann Arbor, MI: University of Michigan,1993.

[8]劉銀華，紀飛翔，葉夏亮. 車身多工位裝配系統可靠性評估與維護策略研究[J].中國機械工程，2016，27(2):273-277.

Liu Yinhua, Ji Feixiang, Ye Xialiang. Study on Reliability Evaluation and Maintenance Policy of the Auto Body Multi-station Assembly System[J]. China Mechanical Engineering, 2016,27(2):273-277.

[9]Cai W, Hu S J, Yuan J X.A Variational Method of Robust Fixture Configuration Design for 3d Workpieces[J]. Journal of Manufacturing Science and Engineering, 1997, 119(11):593-602.

[10]Xiong C H, Xiong Y L. Stability Index and Contact Configuration Planning for Multifingered Grasp[J]. Journal of Robotic Systems, 1998,15(4):183-190.

[11]Jin J, Chen Y. Quality and Reliability Information Integration for Design Evaluation of Fixture System Reliability[J].Quality and Reliability Engineering International, 2001, 17(5): 355-372.

(編輯王旻玥)

收稿日期：2016-02-01

基金項目：國家自然科學基金資助項目(51405299)；上海市自然科學基金資助項目(14ZR1428700)

中圖分類號：TH16

DOI：10.3969/j.issn.1004-132X.2016.13.024

作者簡介：劉銀華，女，1983年生。上海理工大學機械工程學院講師。主要研究方向為車身裝配質量控制與數字化工藝設計。發表論文10余篇。紀飛翔，男，1990年生。上海理工大學機械工程學院碩士研究生。葉夏亮，男，1989年生。上海理工大學機械工程學院碩士研究生。

Optimal Fixture System Design of Auto Bodies Oriented to Assembly System Reliability Analysis

Liu YinhuaJi FeixiangYe Xialiang

University of Shanghai for Science and Technology, Shanghai, 200093

Abstract:In order to describe the gradual decline characteristics of multi-station body assembly system, a reliability model of assembly system for the dimensional quality and fixture system components were established. Combined with the fixture design stability parameter constraints, system reliability of body in white assembly system was proposed oriented multi-station welding process scheme of fixture layout optimization method. Under the given fixture layout, the production cost function of the locating pin was constructed, and the optimization model of the wearing rate of the multi-station fixture was put forward and the distribution was optimized. At last, a body side assembly case was used to illustrate the proposed method, and results show both of the reliability decline process and lifetime of the optimized fixture system are improved.

Key words:auto body assembly; dimensional quality; reliability model; fixture layout; wearing rate