混沌優化神經網絡求解job-shop調度問題研究

趙　莉， 齊耀武

(1.長春大學 機械與車輛工程學院，長春 130022；2.中東長春軌道客車股份有限公司 轉向架制造中心，長春 130062)

?

混沌優化神經網絡求解job-shop調度問題研究

趙莉1， 齊耀武2

(1.長春大學 機械與車輛工程學院，長春 130022；2.中東長春軌道客車股份有限公司 轉向架制造中心，長春 130062)

摘要：針對Job Shop調度問題，建立了離散非線性回饋神經網絡優化模型，給出了一種包含暫態混沌過程的神經網絡優化方法。通過在優化神經網絡中引入一個暫態的混沌過程，使得網絡的演化具備更為靈活的動力學特征。網絡狀態軌跡隨著自反饋系數的衰減，表現為一個典型的倍周期逆分叉過程，逐漸趨向于確定性的非線性回饋神經網絡，并為其提供了一個接近全局最優點的初值。其實質是利用混沌搜索過程的隨機性和狀態遍歷性，加強神經網絡的全局優化能力，避免陷入局部極小點。仿真結果說明本文所建模型和優化方法比傳統的非線性神經網絡優化方法具有更好的收斂性和更高優化能力。

關鍵詞：Job Shop調度；神經網絡優化；混沌優化

0引言

Job-shop(JSP)調度問題是按照一定的時間順序要求分配資源完成加工任務的生產調度問題，是生產過程中經常遇見的問題。研究已證明它是NP困難問題[1，2]。顯然對于此類問題的研究和解決，既具有理論意義，也具有實用價值。在當今研究中，解決此類調度問題的主要方法可分為四類：仿真技術法[3]、組合優化方法[4]、人工智能方法[5]和智能優化方法[6，8]。回饋神經網絡優化是智能優化方法中應用較為廣泛的方法之一，主要包括Hopfild線性回饋神經網絡方法和非線性回饋神經網絡方法[9]。

FooS.Y.P.和Y.Takefuji最早提出將神經網絡用于求解JSP問題，并給出基于Hopfield神經網絡的JSP優化方法。他們通過建立工序交換矩陣和決策成本樹將JSP問題轉換為TSP類型的組合優化問題，并利用玻爾茲曼機和模擬退火方法進行優化求解。在此基礎之上，又有許多學者對其進行研究并擴展和完善了該方法[10-13]。然而此類方法在建模時采用了過多數量的神經元節點，以nxm規模的JSP問題為例其需要建立nm×mn+nm個神經元節點，這使得其難以應用于大規模問題優化。鑒于此，Zhou D.N.等人提出了求解此類問題的非線性回饋神經網絡優化方法[6]。該方法針對任務時間狀態變量建模，對于nxm規模的問題只需建立n×m個神經元節點；并采用梯度搜索進行優化求解。顯然該方法建模復雜度低，更適于進行大規模問題的優化求解。然而該方法在求解過程中，搜索難以保證狀態軌跡的全局遍歷性，簡單的梯度搜索使其非常容易陷入局部極小，甚至導致結果收斂于不可行解，最終影響該方法的優化性能。

為此，本文提出基于混沌神經網絡的JSP優化調度方法。該方法利用非線性回饋神經網絡建立JSP調度問題模型，通過對模型中的神經元增加自反饋，使神經元網絡中形成一暫態時變的倍周期逆分叉過程，并利用混沌動力系統的全局遍歷性避免神經元網絡陷入局部最優點，達到增強算法的全局優化能力的目的。仿真實驗表明，該方法在計算時間和收斂性都有效地提高了原有的非線性回饋神經網絡方法。

1暫態混沌神經網絡JSP調度問題建模

1.1JSP問題描述

JSP調度問題是服從分配和隊列限制的資源分配問題，需要在設備資源上進行加工的工件叫做任務；工件在某臺設備上的加工叫做一道工序或是一個子任務，每個工作是由多道工序或多個子任務組成的，這些工序之間具有先后次序的限制和要求。假設用I={1,2,…,n}代表工作集，用Ki={1,2,…ki}表示工作i的任務集或工序集，Sik表示工作i的第k道工序的開工時間，m(i,k)表示工作i的第k道工序在設備m(i,k)上進行加工，加工時間為ti,k。則JSP調度問題就是滿足下列約束條件的某種準則的優化問題：

(1)

Si1≥0, 1in;

(2)

(3)

其中式(1)表示任何工作的后一工序的加工起始時間一定要大于或等于前一工序的加工結束時間，式(2)表示每一工作的首工序加工起始時間要大于或等于零；式(3)表示在同一設備上加工的兩個工序m(i,k)=m(j,p)，或者工序(i,k)在工序(j,p)前面加工，或者工序(j,p)在工序(i,k)前面加工。在上述約束條件下，根據不同的優化準則可以得到不同JSP調度問題。本文將以所有工作最后一道工序開始時間總和最小為準備，即JSP問題的目標函數為：

(4)

1.2暫態混沌神經網絡JSP調度問題建模

對一n個工作m臺設備的JSP調度問題，可建立一包含n×m個神經元的優化系統，神經元的輸出為工序(i,k)的起始加工時間Si,k，系統輸出狀態集為S=(s11,s12,...,snkn)。與Hopfield神經網絡類似，非線性回饋網絡神經元(i,k)的動態方程和網絡的能量函數可分別描述為：

(5)

(6)

其中，uik是神經元(i,k)的內部狀態，且sik=g(uik)，g(u)是u的單調遞增函數，fik(s)是神經元(i,k)的輸入量，是關于系統輸出狀態集S的非線性函數，C,R分別為容抗和阻抗參數。

根據神經網絡優化的罰函數方法，可將JSP調度問題的目標函數描述為：

其中，A，B，C和D均為系統參數。當x>0時令F1(x)=ebx-bx，F2(x)=ebx-1，否則令F1(x)=F2(x)=0。

令E=I，并對等式兩邊對sik微分可得，

(7)

其中

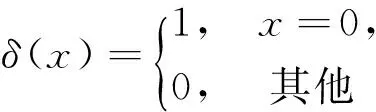
建立非線性回饋神經網絡，并令神經元的輸入fik(s)如(7)式所示，則當所建立的非線性神經網絡能量達到平衡時，系統輸出即為調度問題的優化結果。

前文已指出由(7)式所建立的神經網絡在搜索過程中容易陷入局部極小，甚至導致結果收斂于不可行解。為此，在同步更新模式下，對上述神經網絡進行Eular離散化，

uik_new=α·uik(t)-β·(1+η·zik(t))·fik(s)-zik·(η·sik-s0)

(8)

uik=uik_new

(9)

(10)

(11)

zik_new=H1·γ1·zik(t)+(1-H1)·γ2·zik(t)

(12)

zik=zik_new

(13)

其中，

α是阻尼因子，β是輸入增益系數，0<γ2<γ1<1為衰減系數，z<λ為自反饋控制參數，s0為自反饋偏置參量，ω為輸出比例系數，H1為自適應控制參數，其余皆為系統常數。(8)式為在每一神經元新增一較大反饋后的動態方程，(11)式是(7)式的延伸，是為了保證在同一加工任務的前后工序發生時序沖突時約束傳播的雙向性。

在上述神經網絡模型中，該神經網絡實質上是由能在狀態空間表現出混沌行為的神經元耦合而成的，其基本動力學方程可以描述為：

uik(t+1)=α·uik(t)-zik(t)·(sik(t)-s0)

其中zik(t)·(sik(t)-s0)是神經元的自抑制反饋項，當自反饋系數z增加到一定階段時，系統的動力學過程即呈現出混沌現象。其動態過程如圖1所示。

這種混沌現象具體表現為狀態值動態遞推過程的隨機性和混沌遍歷性。利用狀態軌跡的隨機性可以保證大范圍的搜索能力，利用狀態軌跡的混沌遍歷性則可以保證系統安動力學方程不重復的遍歷所有可能狀態，同時與梯度搜索過程結合，使得神經網絡可以有效的避免局部最小點，收斂至全局最優解。

考察神經元動態方程：

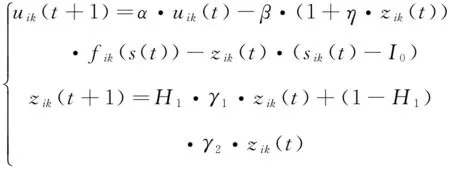
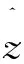
為避免初始反饋增益過大，導致狀態收斂至混沌過程的固有不動點，對影響梯度搜索的輸入增益系數β采用自適應控制，令β′=β·(1+η·z)，即在混沌狀態采用高增益系數，隨者z不斷衰減，系統脫離混沌，β也變化為正常設定值，轉入梯度搜索。

2仿真實驗

為分析混沌神經網絡優化過程中的非線性動力學特性，對n=4,m=3的JSP調度問題進行仿真，系統參數如表1、表2所示。

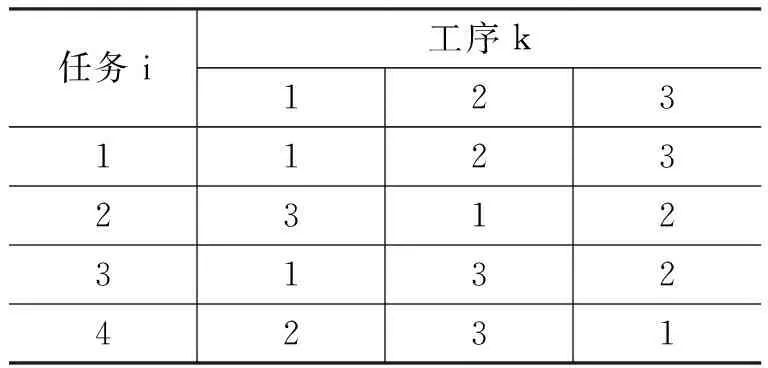
表1　工序分配表m(i,k)

表2工序時間表

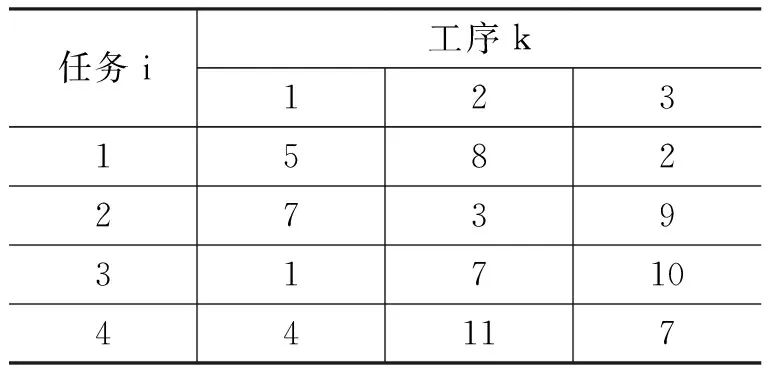
任務i工序k123158227393171044117

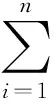
適當調整系統初始狀態值U(0)，當系統收斂時，可以得到經優化的各工序起始加工時間sik如表3所示，系統甘特圖如圖3所示。

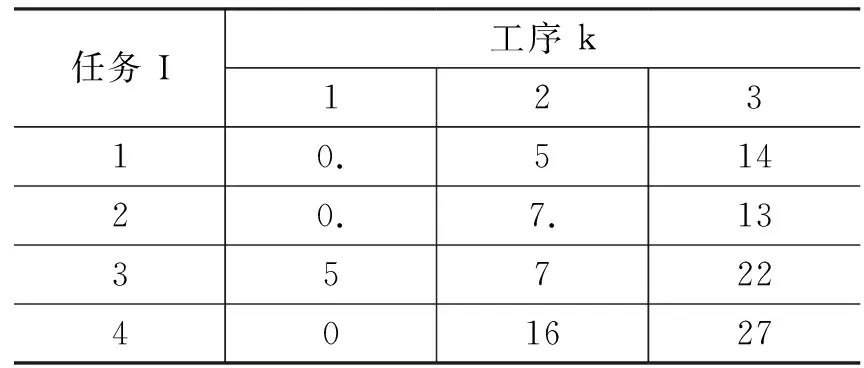
表3　工序起始加工時間sik

由系統運行軌跡圖可看出，在搜索開始階段控制參數z較大，自抑制反饋很強，系統進入混沌搜索過程，輸出狀態與系統內部狀態軌跡呈現出隨機性與狀態遍歷性。此后控制參數z轉而進入時變衰減，混沌軌跡表現為一個倍周期逆分叉的收斂軌跡，混沌現象逐漸消失，系統恢復為梯度搜索，直至得到最后結果。

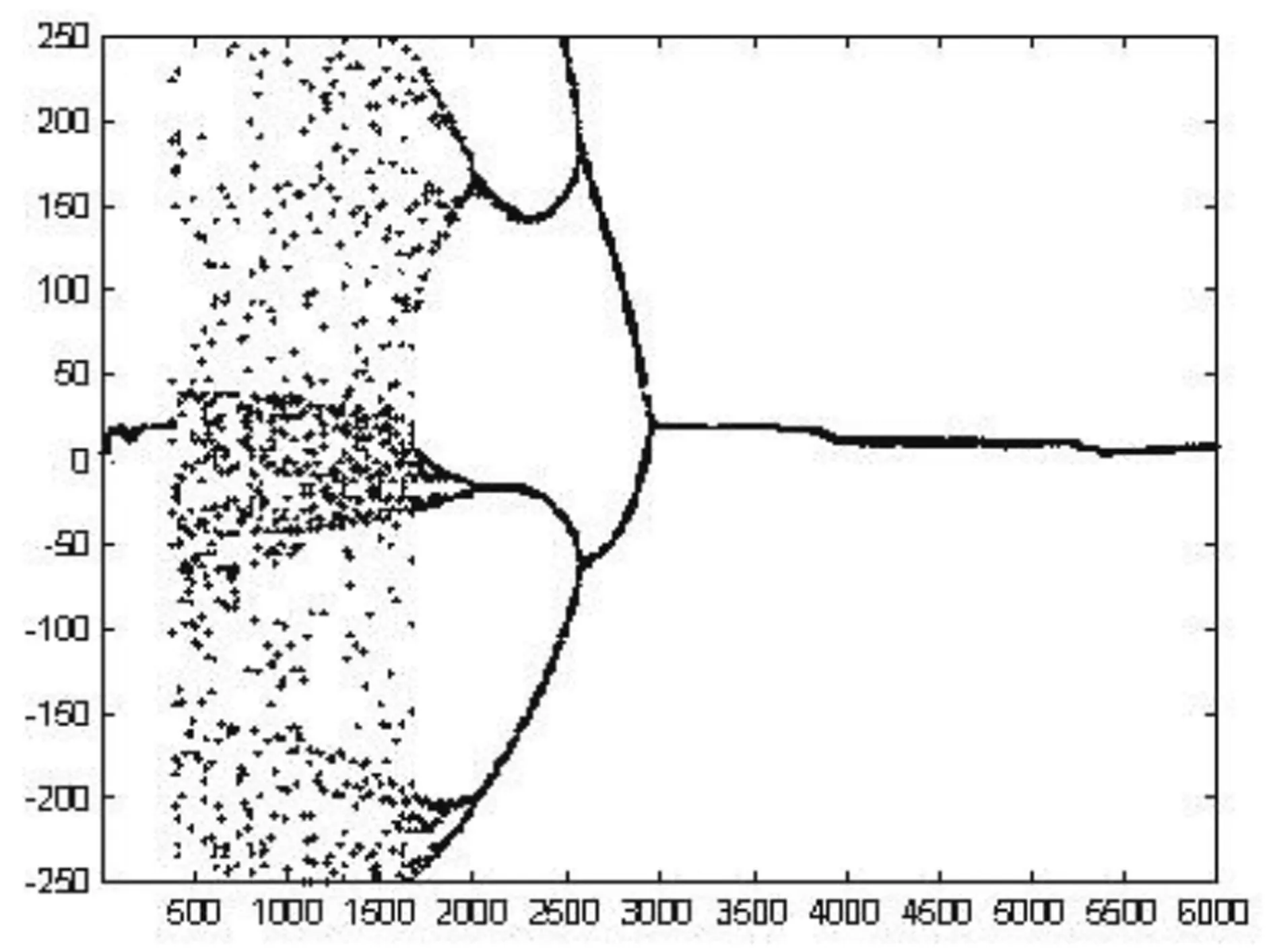
圖1(a)系統的動力學過程樣力1圖

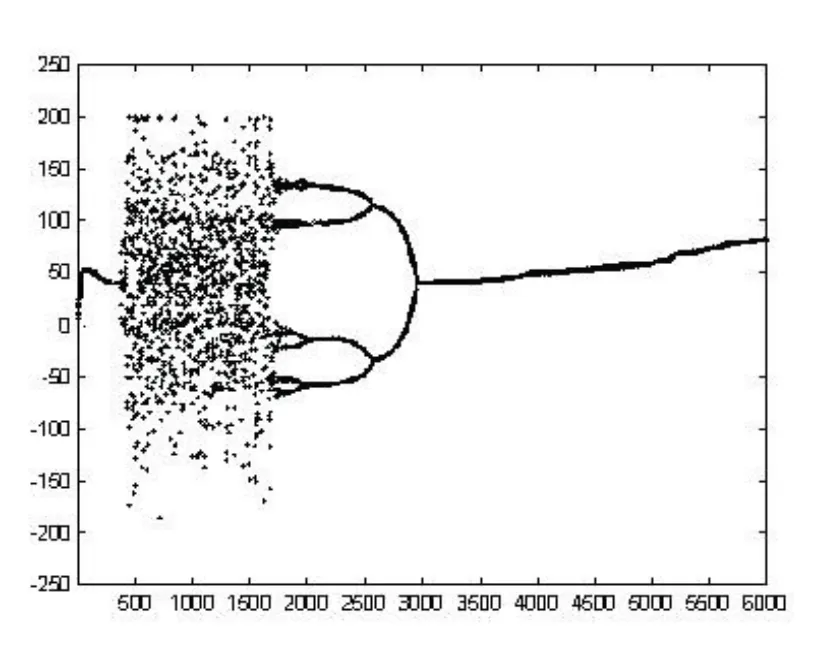
圖1(b)系統的動力學過程樣力2圖

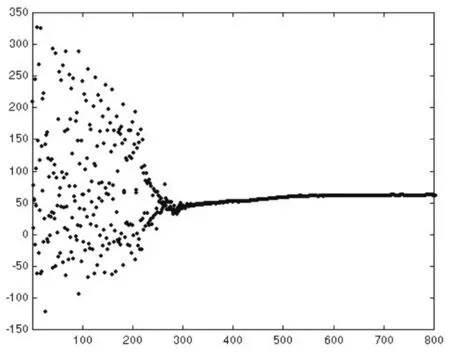
圖2(a) uik動力學軌跡圖

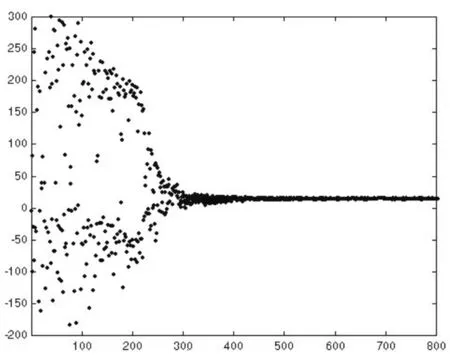
圖2(b) uik動力學軌跡圖

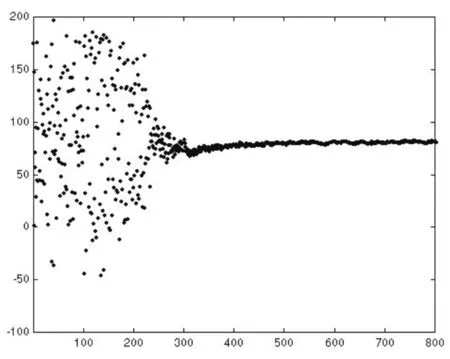
圖2(c)目標函數Siki的動力學軌跡圖

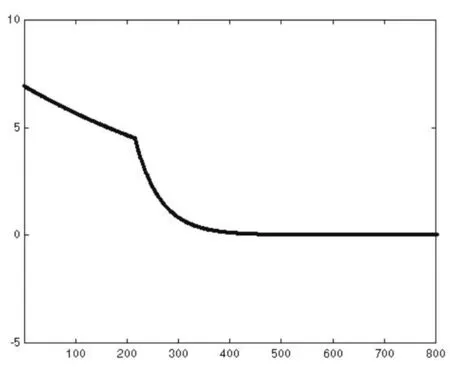
圖2(d)自反饋控制參數z的動態軌跡圖

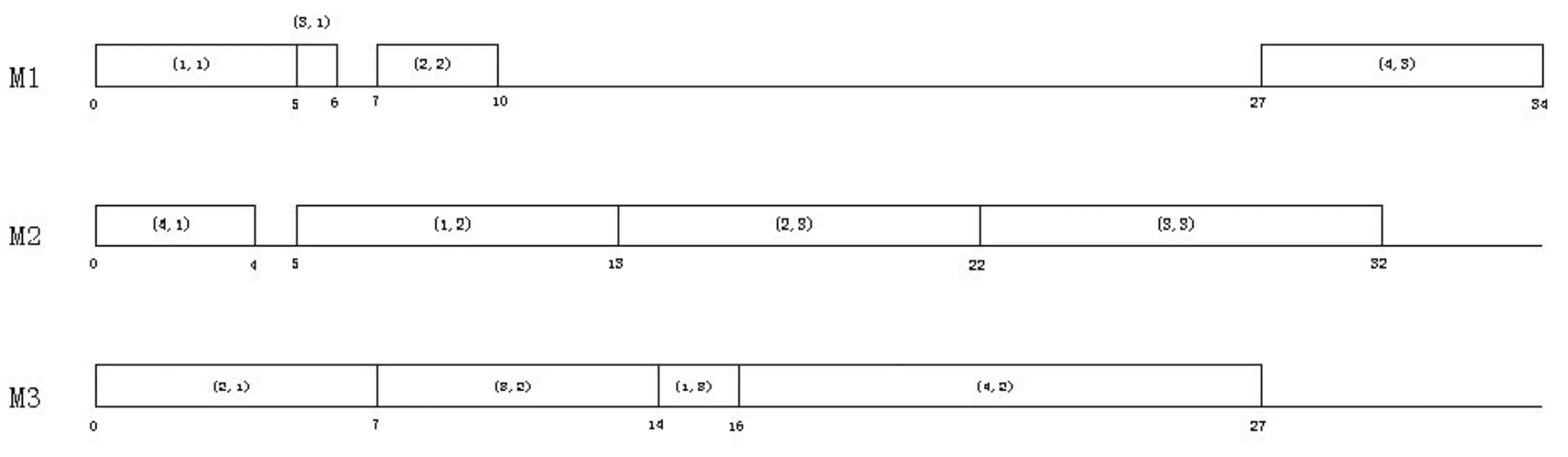
圖3　系統甘特圖

在區間[0,5]上選取兩初始狀態值U′(0)和U″(0)，在相同條件下對暫態混沌神經網絡和非線性回饋神經網絡分別進行優化，定義滿意解為與最優解相差小于5%，其輸出優化結果分別如圖4(a)，(b)，(c)和(d)所示。

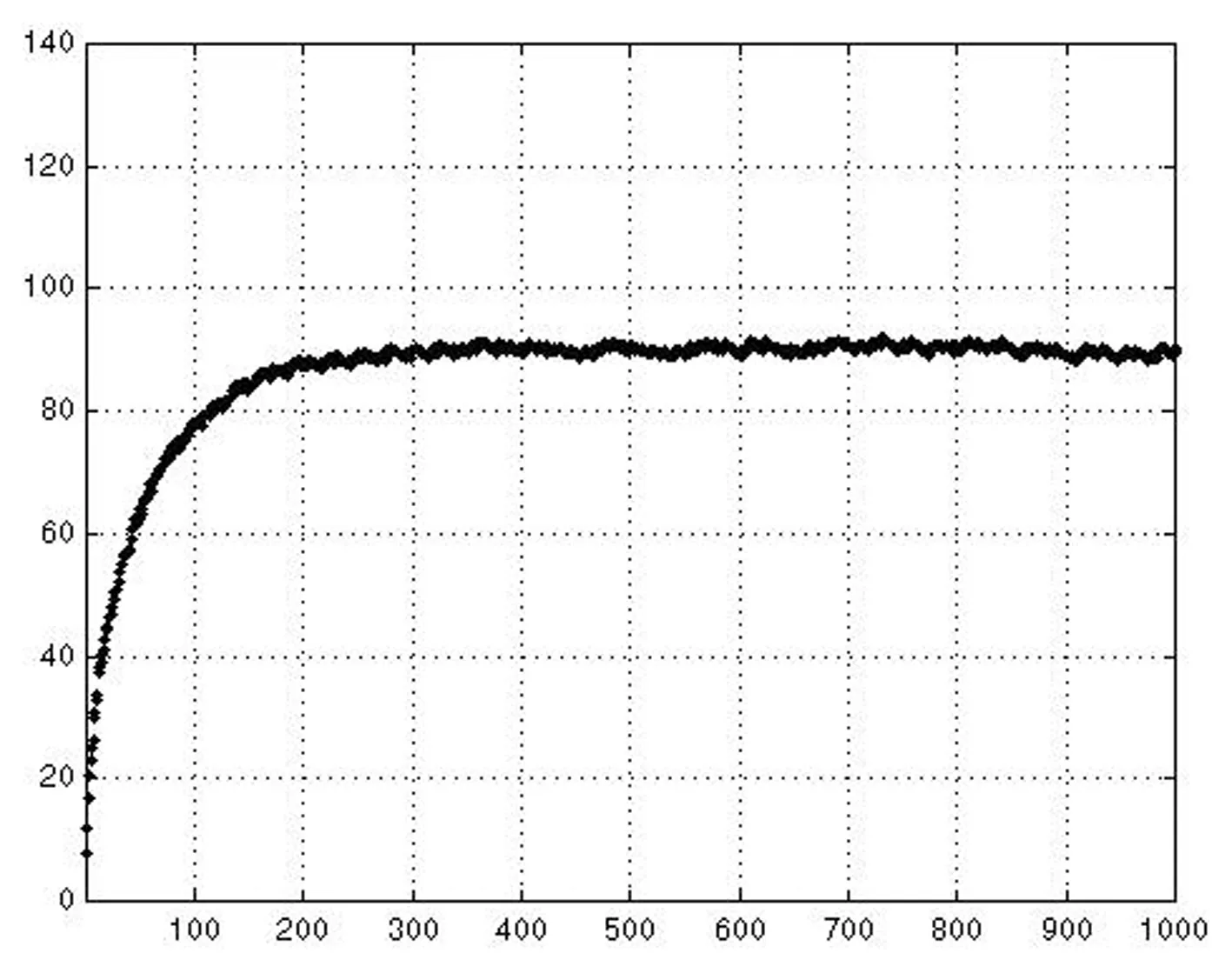
圖4(a)初始狀態值U′(0)非線性回饋神經網絡優化結果輸出圖

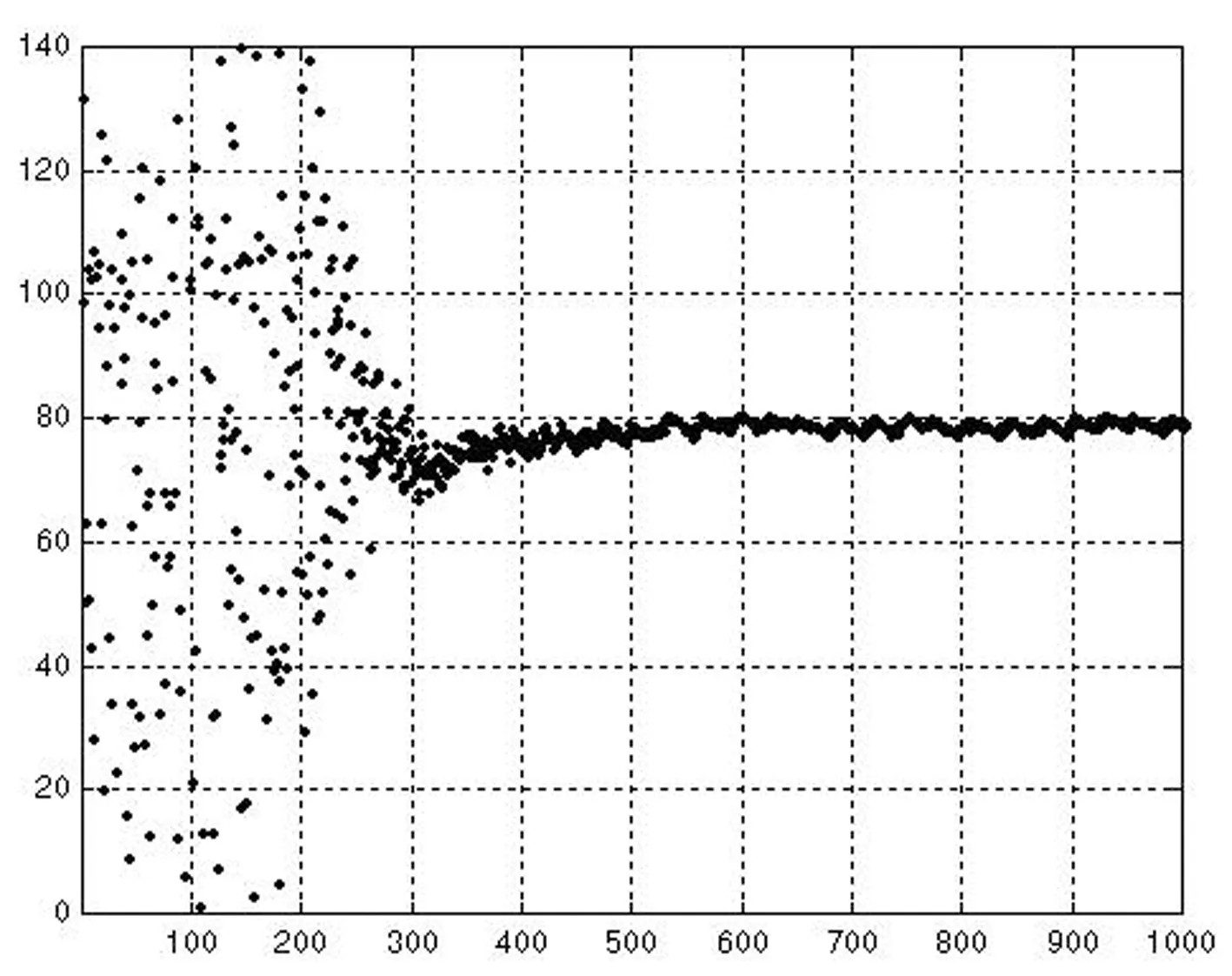
圖4(b)初始狀態值U′(0) 暫態混沌神經網絡優化結果輸出圖

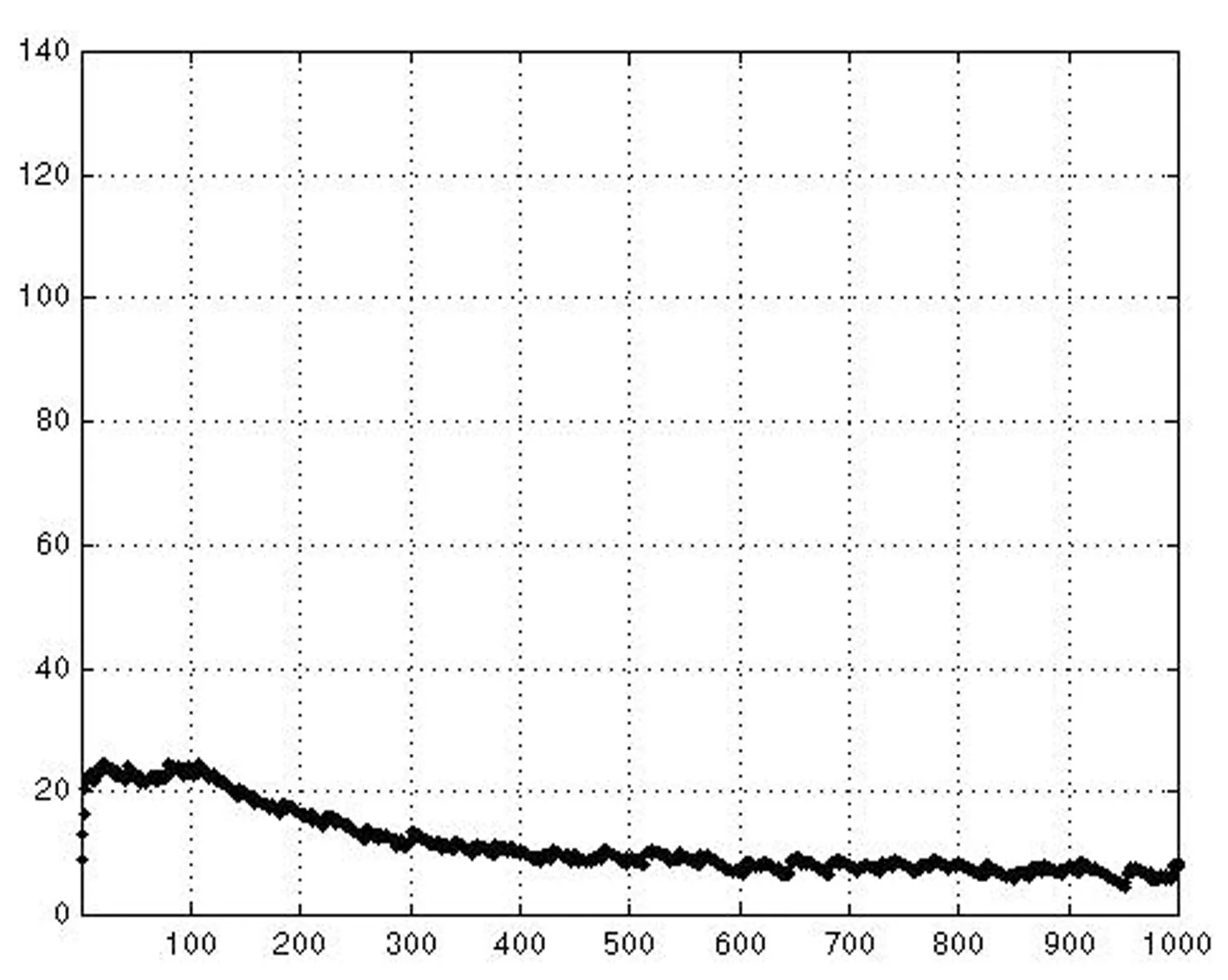
圖4(c)初始狀態值U″(0) 非線性回饋神經網絡優化結果輸出圖

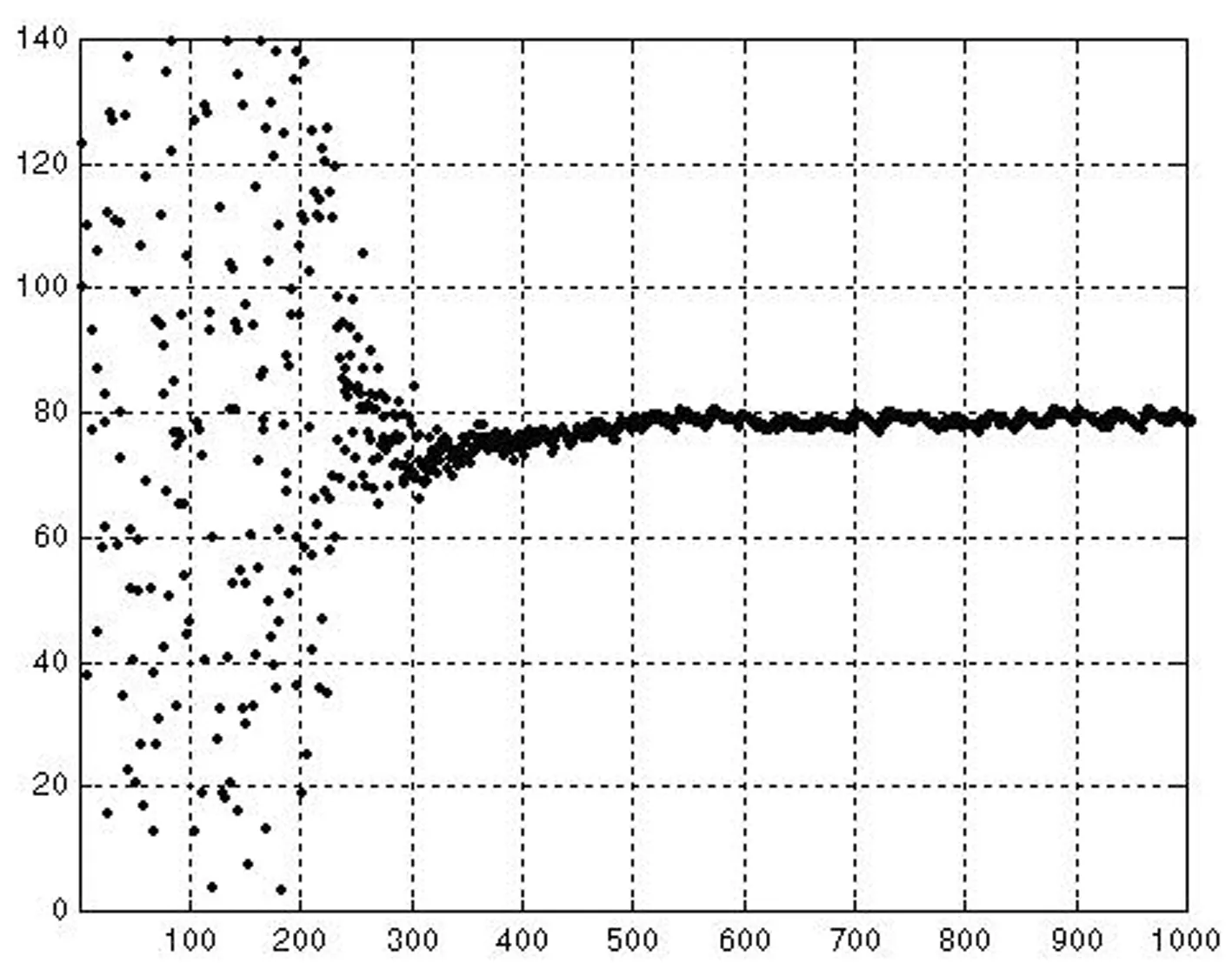
圖4(d)初始狀態值U″(0)暫態混沌神經網絡優化結果輸出圖

通過上述結果可以看出，在初始狀態條件下，一般非線性回饋神經網絡一次收斂于一般有效解，一次收斂于非法解，而暫態混沌神經網絡則均收斂于滿意解，優化效果明顯好于前者。此外，再分別對普通非線性回饋網絡與混沌神經網絡進行200次優化仿真，其優化結果如下。

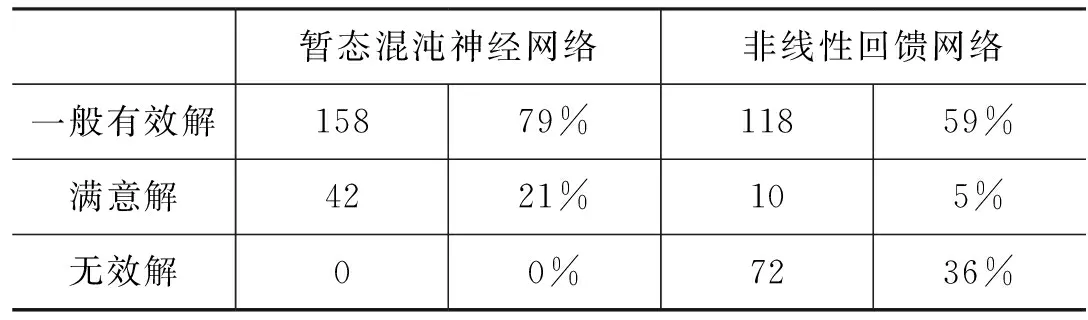
表4　優化性能比較

由上述仿真結果可以看出，增加了暫態混沌過程的神經網絡，由于混沌過程的隨機性和混沌遍歷性，使得神經網絡系統一方面具備大范圍的搜索能力，系統狀態可以安動力學方程不重復的遍歷多種可能狀態，有效避免能量函數的局部最小點，另一方面可以也減弱系統的初值敏感性，減少系統由于狀態初值選擇不恰當而收斂至不可行解的可能性。上述仿真實驗結果對此給出了很好的驗證。

3結論

本文針對JSP調度問題，給出了一種包含暫態混沌過程的非線性回饋神經網絡優化方法。通過引入一個暫態的混沌過程，使得神經網絡的演化具備更為靈活的動力學特征。隨著自反饋系數的不斷衰減，網絡狀態軌跡表現為一個倍周期逆分叉過程，并逐漸趨向于確定性的非線性回饋神經網絡，并為其提供了一個接近全局最優點的初值。其實質是利用混沌搜索過程的隨機性和狀態遍歷性，加強神經網絡的全局優化能力，避免陷入局部極小點。仿真結果說明了本文所建模型和優化方法的有效性。

參考文獻：

[1]Foosy Takefujuy.Stochastic neural networks for solving job-shop scheduling: Parts I problem representation [C].Proceeding of the IEEE International Conference on Neural Networks,1988,275-282.

[2]Foosy Takefujuy. Stochastic neural networks for solving job-shop scheduling:Parts II .Architecture and simulations [C].Proceeding of the IEEE International Conference on Neural Networks,1988.283-290.

[3]Kiran Allen,Simth,Williamas.Job-Shop調度中的仿真研究[C].鄭彥譯，計算機集成制造系統譯文集，北京：中國科學院自動化研究所，1988.

[4]Alan Smith Manne, On the Job-Shop Scheduling Problem [J]. Operations Research,1959,7(2):123-132.

[5]Eseale.Benaana,Gucci.Bel and David.Dubois.OPAL:A multi knowledge-based system for industrial job-shop scheduling [J].International Journal Production Research,1988,26(5):795-819.

[6]劉民，孫元凱，吳澄.TS+BS混合算法及其在job-shop調度問題上的應用[J].清華大學學報，2002,42(3):424-426.

[7]潘全科，王文宏，朱劍英.基于粒子群優化和模擬退火的混合調度算法[J].中國機械工程，2006(10):953-957.

[8]韓世芬.基于模擬退火算法的Job Shop問題研究[J].電腦與電信，2007(7):612-615.

[9]朱顥.基于智能優化算法的Job Shop調度問題的研究[D].天津：天津大學，2004.

[10]Zhou Deming,Charkassky Vladimir,Baldwin Tred.et al.Scaling neural network for job-shop scheduling [A].Proceedings IEEE International Joint Conference on Neural Networks[C].1989.889-894.

[11]Willems Thomas, Brandts Lem. Implementing heuristics as an optimization criterion in neural net works for job shop scheduling[J]. Journal of Intelligent Manufacturing, 1995; 6(2): 377-387.

[12]Chang Shui Zhang, Ping Fan Yan, Chang Tong. Solving job-shop scheduling problem with priority using neural net work [C]. Proceedings IEEE International Joint Conference on Neural Networks，1991，1361-1366.

[13]張長水,閻平凡.解Job-shop調度問題的神經網絡方法[J].自動化學報, 1995, 21(6 ):706-712.

責任編輯：程艷艷

Research on a Solution to Job-shop Schedule Problems by Neural Network with Chaotic Optimization

ZHAO Li， QI Yaowu2

(1.College of Machinery and Vehicle Engineering, Changchun University, Changchun 130022, China；2.Bogie Manufacture Center,CRRC Changchun Railway Vehicles Co., Ltd., Changchun 130062, China)

Abstract：In view of Job-shop schedule problems, an optimized model of disperse nonlinear feedback neural network is established, and a neural network optimization method with transient chaos is given, which introduces a process of transient chaos to an optimized neural network, making its evolution have flexible dynamics features. With the reduction of self-feedback coefficient, the state trajectory is shown as a typical inverse bifurcation process, converging to a definite nonlinear feedback neural network and providing a globally near-optimal solution. The essence is to improve the global optimization ability by the randomness and ergodicity of chaos searching, so as to avoid sticking into the local minima. Simulation results indicate that the established model and optimized method have better convergence and higher optimization ability than the traditional nonlinear neural network optimization method.

Keywords：Job-shop schedule; neural network optimization; chaos optimization

收稿日期：2016-04

基金項目：吉林省計算與軟件科學創新平臺基金資助(60374061)

作者簡介：趙莉(1972-)，女，吉林長春人，副教授，碩士，主要從事工業工程及計算機應用方面研究。

中圖分類號：TP18TP301

文獻標志碼：A

文章編號：1009-3907(2016)06-0006-07