基于奇異值分解的Toeplitz結構測量矩陣構造方法

趙　輝　金勝杰

(重慶郵電大學光通信與網絡重點實驗室　重慶 400065)

?

基于奇異值分解的Toeplitz結構測量矩陣構造方法

趙輝金勝杰

(重慶郵電大學光通信與網絡重點實驗室重慶 400065)

摘要在壓縮感知CS(Compressed Sensing)理論中，測量矩陣的構造至關重要，其性能直接影響到數據壓縮采樣的效率及信號的重構質量。針對Toeplitz結構測量矩陣重構性能不高的問題，提出一種基于奇異值分解的Toeplitz結構測量矩陣構造方法。首先對Toeplitz矩陣進行奇異值分解，然后通過對該矩陣的非零奇異值進行優化來提高矩陣的列向量獨立性，從而提高其重構性能。仿真結果表明，相比較未優化的Toeplitz結構測量矩陣以及當前常用的高斯隨機矩陣，當采用優化后的Toeplitz結構測量矩陣對信號進行壓縮感知時，信號的重構精度得到顯著提高。

關鍵詞壓縮感知測量矩陣托普利茲結構奇異值分解信號重構

0引言

壓縮感知CS[1,2]理論突破了奈奎斯特采樣定理對信號采集與處理的限制，實現了數據采集與數據壓縮的同時進行。在很大程度上減少了數據采樣所需要的時間和存儲數據所需要的空間，為圖像信號的采集和壓縮的研究提供了一種新的理論依據。在壓縮感知理論中，測量矩陣性能的優劣直接關系到信號重建精度的高低與重構速度的快慢。當前常用的測量矩陣大部分是隨機的，然而，這類矩陣通常不易于硬件實現，由于將測量矩陣予以硬件實現是壓縮感知理論應用到實際中的一個重要條件。因此，構造具有較高重構性能并且易于硬件實現的的測量矩陣具有重要意義。

根據矩陣元素的隨機性和確定性可將測量矩陣分為兩類，即隨機測量矩陣和確定性測量矩陣[3]。隨機測量矩陣包含高斯隨機矩陣、稀疏投影矩陣以及貝努利矩陣等。其主要特點是矩陣的每個元素都服從獨立同分布，因此隨機測量矩陣的列向量具有較好的非相關性，所以只需較少的采樣值就能完成原信號的精確重建。但是，隨機測量矩陣占用存儲空間較大、計算復雜度高且難以硬件實現。確定性矩陣包括Toeplitz結構測量矩陣、循環矩陣等，其主要特點是易于硬件實現，但相比較隨機測量矩陣，其重構性能較低。在確定性測量矩陣中[4-7]，Toeplitz結構測量矩陣是通過行向量的循環移位來構造整個矩陣。在實際應用過程中，這種循環移位非常易于硬件實現，并且Toeplitz矩陣是一種高度結構化的矩陣，矩陣的結構化可以提升計算速度及降低計算復雜度。然而同大多數確定性測量矩陣[8,9]一樣，Toeplitz矩陣相比較高斯隨機矩陣等隨機測量矩陣也存在重建精度不高的問題[10-12]。為了確保原信號進行較高精度的重建，通常需要較多數目的測量值，而在實際應用中獲得較多測量值需要付出很大的代價。

針對易于硬件實現的Toeplitz矩陣重構性能較低的問題，本文提出一種基于奇異值分解的Toeplitz結構測量矩陣構造方法。通過對該矩陣的奇異值進行優化來提高測量矩陣的列向量獨立性，從而提高其重構性能。仿真結果表明：在相同的稀疏基和重構算法下，無論是重構圖像的視覺效果還是重構圖像的客觀評價指標數值，當采用本文方法優化后的Toeplitz結構測量矩陣進行壓縮感知時，總體上圖像信號重構結果要好于采用未優化的Toeplitz測量矩陣和高斯隨機矩陣時的情況，即本文構造的基于奇異值分解的Toeplitz結構測量矩陣具有較好的重構性能。

1壓縮感知理論框架

1.1壓縮感知理論的數學模型

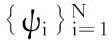
(1)

其中，式(1)中Ψ=[ψ1,ψ2,…,ψN]為N×N的正交基矩陣，θ=[θ1,θ2,…,θN]T為系數向量。若系數向量θ中只有K(K?N)個非零系數，那么稱信號x在基矩陣Ψ下為K稀疏信號。將信號x投影到與稀疏基不相關的測量矩陣ΦM×N(M?N)上，即對信號x執行壓縮觀測，可得：

y=Φx=ΦΨθ

(2)

信號的重建就是通過M維的測量值y來恢復N維的原始信號x，由于測量值維數M?N，因此求解式(2)的過程是病態的，即無法直接求解。但是若原信號x是稀疏的或可壓縮的，且測量矩陣滿足有限等距性質RIP(RestrictedIsometryPrinciple)[1,2]，那么可通過求解下述最小l0范數問題來精確求解原始信號x，即：

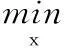
(3)

由于對l0范數問題的求解是NP-hard的，且最小l0范數問題和最小l1范數問題在測量矩陣滿足RIP的條件下是等價的[1]，因此式(3)可轉化為：

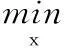
(4)

壓縮感知過程如圖1所示。

圖1壓縮感知過程

1.2測量矩陣滿足的約束條件

測量矩陣是壓縮感知理論的重要組成部分，為了確保信號進行有效的壓縮和精確的重構，測量矩陣應滿足一定的條件。Candes等人提出了測量矩陣所滿足的RIP準則[13]，該準則的數學描述為：對于任意K稀疏信號x和常數δK∈(0,1)，如果：

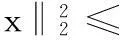
(5)

成立，則稱測量矩陣滿足有限等距性質。

在測量矩陣的構造過程中，幾乎很難驗證矩陣是否滿足RIP條件。通常可以采用同RIP準則等價的性質，即矩陣非相干性[14,15]來作為測量矩陣構造的理論指導。研究表明：在正交稀疏基Ψ確定的情況下，可從測量矩陣的列向量相關性方面入手設計測量矩陣。為了指導構造測量矩陣，在文獻[1]中Donoho給出了測量矩陣所要滿足的三個基本特征：(1) 由測量矩陣的列向量組成的子矩陣的最小奇異值必須大于一定的常數，即測量矩陣的列向量在一定程度上要具有較好的線性非相干性；(2) 測量矩陣的列向量要滿足一定程度上的隨機性；(3) 在一定稀疏度條件下的解則為滿足1-范數最小的列向量。這三個特征為測量矩陣的構造提供了重要指導，同時也是本文測量矩陣優化算法的重要理論依據。

2基于奇異值分解的Toeplitz結構測量矩陣構造方法

奇異值分解SVD(SingularValueDecomposition)廣泛應用于信號與圖像處理、最小二乘問題、酉不變范數理論、特征值問題以及優化問題等領域。它是矩陣論和線性代數中一種很重要的矩陣分解算法[16-21]。

2.1矩陣奇異值分解

(6)

其中，Σ=diag(δ1,δ2,…,δr)，U滿足UHAAHU是對角矩陣，V滿足VHAHAV是對角矩陣。那么稱式(6)為矩陣A的奇異值分解。矩陣奇異值分解具有以下主要性質：

性質1矩陣非零奇異值的個數與該矩陣的秩相等。設矩陣A∈Cm×n，且其秩rank(A)=r，則A的奇異值滿足σ1≥σ2≥…≥σr>σr+1=…=σm=0。

2.2基于奇異值分解的Toeplitz結構測量矩陣優化算法

測量矩陣要滿足的第一個特征指出：測量矩陣的列向量要具有比較好的線性非相關性，然而矩陣的線性非相關性與矩陣的最小奇異值密切相關。若矩陣的最小奇異值越小，那么矩陣的線性相關性越大，即其獨立性越弱。當測量矩陣最小的奇異值近似為0時，則矩陣列向量的線性獨立性趨于最小。因此，本文提出了一種基于奇異值分解的Toeplitz結構測量矩陣設計方法，目的是通過增大矩陣的奇異值來提高矩陣列向量的線性獨立性。

通常情況下，理論上常用的測量矩陣在實際應用中具有局限性，難以硬件實現，滿足一定條件的測量矩陣才能更好地予以硬件實現。文獻[3]給出了能在實際中應用的測量矩陣應滿足以下性質：(1) 測量矩陣和稀疏基矩陣要具有較強的不相干性，以確保信號進行較高精度的重建；(2) 測量值的數目要盡量與理論值相接近，以降低獲取測量值的成本；(3) 矩陣要具有較強的結構性，以減小采樣與重建的復雜度；(4) 占用存儲空間小，構造元素簡單，并且易于硬件實現。因此，為了使構造的Toeplitz結構測量矩陣結構簡單，并且能夠更好地通過實際硬件予以實現，那么該矩陣的元素可由0、1來組成。

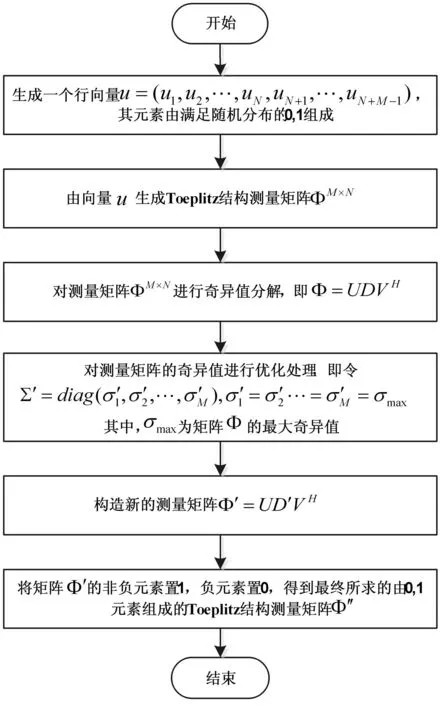
綜上，該方法首先生成一個元素由0、1隨機組成的行向量u=(u1,u2,…,uN,uN+1,…,uN+M-1)。然后根據向量u來構造Toeplitz結構測量矩陣Φ，接下來對測量矩陣Φ進行奇異值分解，并對奇異值進行優化處理，得到新的測量矩陣Φ′。并且該優化過程并沒有改變矩陣非零奇異值的個數，因此，由性質1可知，該優化過程并沒有改變矩陣的秩。然后再根據性質2和推論1，對新構造的測量矩陣Φ′作負元素置0，非負元素置1的近似處理，得到最終由0、1元素組成的Toeplitz結構測量矩陣Φ″。具體步驟如下：

步驟1生成一個隨機向量u，其元素由滿足隨機分布的0、1組成，即u=(u1,u2,…,uN,uN+1,…,uN+M-1)；

步驟2利用步驟1生成的向量u構造Toeplitz結構測量矩陣Φ∈RM×N(M

(7)

步驟3對矩陣Φ∈RM×N(M

(8)

其中矩陣U、V分別為M×M維和N×N維的酉矩陣，Σ=diag(σ1,σ2,…,σM)，σ1≥σ2≥…≥σM為矩陣Φ的非零奇異值；

步驟5構造新的測量矩陣Φ′。

(9)

步驟6將矩陣Φ′的元素進行近似處理，即將測量矩陣Φ′中非負元素置1，負元素置0，得到最終所求測量矩陣Φ″。

對Toeplitz結構測量矩陣進行優化的流程如圖2所示。

圖2　優化算法流程圖

3仿真結果與分析

為了驗證本文提出的基于奇異值分解算法構造的Toeplitz結構測量矩陣的性能，采用兩幅標準灰度測試圖像Lena和Peppers進行仿真，且這兩幅圖像的分辨率均為256×256。各個測量矩陣在圖像的壓縮感知過程中采用相同的稀疏變換基和重構算法，即首先對這兩幅圖像采用小波變換進行稀疏表示。然后再分別利用高斯隨機矩陣、元素由0、1組成的Toeplitz結構測量矩陣以及采用本文算法優化后的由0、1元素組成的Toeplitz結構測量矩陣對稀疏變換后的圖像信號進行壓縮投影。最后選用OMP重構算法來重構原始圖像。

本文通過重構圖像的峰值信噪比PSNR和圖像匹配度match兩項指標來對圖像的重構質量進行衡量。峰值信噪比和匹配度的定義如下：

PSNR=10lg(2552/MSE)

(10)

同樣地，重構圖像匹配度match可表示為：

(11)

表1和表2分別表示當測量矩陣為未優化的Toeplitz測量矩陣、高斯隨機矩陣以及本文算法優化后的Toeplitz測量矩陣時，重構圖像的峰值信噪比及圖像匹配度隨采樣率變化的仿真結果比較。

表1　測試圖像仿真結果峰值信噪比值比較

表2　測試圖像仿真結果匹配度值比較

由表1和表2可知，重構圖像的峰值信噪比和圖像匹配度均隨著采樣率的增大而增加。從表1可以明顯看出，當信號采樣率一定的情況下，采用優化后的Toeplitz結構矩陣作為測量矩陣時，重構圖像的PSNR值要高于采用高斯隨機矩陣和未優化的Toeplitz矩陣作為測量矩陣時的情況。同樣地，從表2可以得到，當測量矩陣為優化后的Toeplitz矩陣時，在采樣率相同的條件下，重構圖像的匹配度要高于采用其他兩種測量矩陣時的情況。表1和表2的仿真結果說明采用本文算法優化后的Toeplitz結構測量矩陣的重構性能得到顯著提高。

為了直觀驗證優化后的Toeplitz結構測量矩陣的重構性能，圖3與圖4分別給出了不同采樣率下Lena圖像與Peppers圖像采用高斯隨機矩陣、Toeplitz結構測量矩陣及優化后的Toeplitz結構測量矩陣進行觀測時的峰值信噪比對比圖；同樣地，圖5與圖6分別給出了不同采樣率下這兩幅圖像采用高斯隨機矩陣、Toeplitz結構測量矩陣及優化后的Toeplitz結構測量矩陣進行觀測時的匹配度對比圖。

圖3　Lena圖像在不同測量矩陣下的PSNR值比較

圖4　Peppers圖像在不同測量矩陣下的PSNR值比較

圖5　Lena圖像在不同測量矩陣下的match值比較

圖6　Peppers圖像在不同測量矩陣下的match值比較

從圖3和圖4可以看出，隨著采樣率的增大，圖像的峰值信噪比逐漸增加，表明這幾種測量矩陣的重構效果隨著采樣率的增大逐漸增強。此外，在相同的采樣率下，當測量矩陣為高斯隨機矩陣時，重構圖像的PSNR值大于測量矩陣為未優化的Toeplitz矩陣時的情況。而本文對Toeplitz矩陣進行優化處理后，其重構圖像的PSNR值又大于采用高斯隨機矩陣時的情況。并且在采樣率大于0.5時，重構圖像PSNR值趨于近似線性增加。

同樣由圖5和圖6可得，采用優化后的Toeplitz矩陣作為測量矩陣時，在同樣的采樣率下，重構圖像的匹配度值大于采用高斯隨機矩陣和未優化的Toeplitz矩陣時的情況，表明優化后的Toeplitz矩陣具有較高的重構精度。因此，本文對Toeplitz矩陣優化后，可顯著提高重建圖像的PSNR值及匹配度值。

為了進一步對比高斯隨機矩陣、Toeplitz結構測量矩陣、優化后的Toeplitz結構測量矩陣的重構性能，圖7和圖8分別給出了Lena與Peppers圖像在相同的稀疏基和重構算法下，當采樣率為0.5時重構圖像的視覺效果比較。

圖7　Lena圖像在采樣率為0.5時的重構效果圖

圖8　Peppers圖像在采樣率為0.5時的重構效果圖

從圖7和圖8可以看出，當采樣率取值0.5時，測量矩陣為高斯隨機矩陣時重構圖像的視覺效果要優于測量矩陣為未優化的Toeplitz矩陣的情況。并且當測量矩陣為優化后的Toeplitz結構測量矩陣時，重構圖像的視覺效果又好于采用高斯隨機矩陣的情況。尤其是采用優化后的Toeplitz結構測量矩陣對圖像進行壓縮觀測時，重構圖像的邊緣及輪廓更加清晰，塊效應較弱，即顯著提高了圖像重建質量。

4結語

針對易于硬件實現的Toeplitz結構測量矩陣重建精度不高的問題，本文提出了一種基于奇異值分解的Toeplitz結構測量矩陣優化方法。將Toeplitz結構測量矩陣進行奇異值分解，并對該矩陣的奇異值進行優化處理，通過增大矩陣的奇異值來提其列向量線性獨立性，進而提高其重構性能。仿真結果表明：相比較當前常用的高斯隨機矩陣以及未優化的Toeplitz結構測量矩陣，采用本文提出的基于奇異值分解的Toeplitz結構測量矩陣作為測量矩陣進行圖像信號壓縮感知時，重構圖像的匹配度、PSNR值均得到了顯著提高，并且重構圖像的主觀視覺效果也得到了明顯提升。因此，本文提出的Toeplitz結構測量矩陣優化方法有效提高了該測量矩陣的重構性能。

參考文獻

[1]DonohoDL.Compressedsensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289-1306.

[2] 焦李成,楊淑媛,劉芳,等.壓縮感知回顧與展望[J].電子學報,2011,39(7):1651-1662.

[3] 秦周.壓縮感知中測量矩陣的優化與構造方法[D].北京:北京交通大學,2012.

[4]MonajemiH,JafarpourS,GavishM,etal.DeterministicmatricesmatchingtheCompressedSensingphasetransitionsofGaussianrandommatrices[J].ProceedingsoftheNationalAcademyofSciences,2013,110(4):1181-1186.

[5]TehraniAS,DimakisAG,AireG.OptimaldeterministicCompressedSensingmatrices[C]//IEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing(ICASSP).Vancouver:IEEEPress,2013:5895-5899.

[6]LiS,GeG.Deterministicsensingmatricesarisingfromnearorthogonalsystems[J].IEEETransactionsonInformationTheory,2014,60(4):2291-2302.

[7] 王強,李佳,沈毅.壓縮感知中確定性測量矩陣構造算法綜述[J].電子學報,2013,41(10):2041-2050.

[8]BlanchardJD.TowarddeterministicCompressedSensing[J].ProceedingsoftheNationalAcademyofSciences,2013,110(4):1146-1147.

[9]LiKezhi,LuGan,CongLing.ConvolutionalCompressedSensingusingdeterministicsequences[J].IEEETransactionsonSignalProcessing,2013,61(3):740-752.

[10]HauptJ,BajwaWU,RazGM,etal.ToeplitzCompressedSensingmatriceswithapplicationstosparsechannelestimation[J].IEEETransactionsonInformationTheory,2010,56(11):5862-5875.

[11]SebertF,ZouYiming,YingLeslie.ToeplitzblockmatricesinCompressedSensingandtheirapplicationsinimaging[C]//IEEE.InformationTechnologyandApplicationsinBiomedicine(ITAB).Shenzhen:IEEEpress2008:47-50.

[12]BajwaWU,HauptJD,RazGM,etal.Toeplitz-structuredCompressedSensingmatrices[C]//IEEE.StatisticalSignalProcessing(SSP).Madison,USA:IEEEPress,2007:294-298.

[13]CandèsEJ,RombergJ,TaoT.Robustuncertaintyprinciples:Exactsignalreconstructionfromhighlyincompletefrequencyinformation[J].IEEETransactionsonInformationTheory,2006,52(2):489-509.

[14]BlumensathT.CompressedSensingwithnonlinearobservationsandrelatednonlinearoptimizationproblems[J].IEEETransactionsonInformationTheory,2013,59(6):3466-3474.

[15]EladM.OptimizedprojectionsforCompressedSensing[J].IEEETransactionsonSignalProcessing,2007,55(12):5695-5702.

[16]LaiCC,TsaiCC.Digitalimagewatermarkingusingdiscretewavelettransformandsingularvaluedecomposition[J].IEEETransactionsonInstrumentationandMeasurement,2010,59(11):3060-3063.

[17]KleibergenF,PaapR.Generalizedreducedranktestsusingthesingularvaluedecomposition[J].Journalofeconometrics,2006,133(1):97-126.

[18]CajJianfeng,CandèsEJ,ShenZuowei.Asingularvaluethresholdingalgorithmformatrixcompletion[J].SIAMJournalonOptimization,2010,20(4):1956-1982.

[19]CongedoM,PhlypoR,PhamDT.Approximatejointsingularvaluedecompositionofanasymmetricrectangularmatrixset[J].IEEETransactionsonSignalProcessing,2011,59(1):415-424.

[20]SatoH,IwaiT.ARiemannianoptimizationapproachtothematrixsingularvaluedecomposition[J].SIAMJournalonOptimization,2013,23(1):188-212.

[21]SavasB,EldénL.Handwrittendigitclassificationusinghigherordersingularvaluedecomposition[J].Patternrecognition,2007,40(3):993-1003.

TOEPLITZ STRUCTURE MEASUREMENT MATRIX CONSTRUCTION METHOD BASEDONSINGULARVALUEDECOMPOSITION

Zhao HuiJin Shengjie

(Key Laboratory of Optical Communication and Networks,Chongqing University of Posts and Telecommunictions,Chongqing 400065,China)

AbstractThe construction of measurement matrix is crucial to compressed sensing theory, its performance directly affects the efficiency of data sampling compression and the quality of signal reconstruction. In view of the fact that the performance of Toeplitz structure measurement matrix reconstruction is not high, we proposed a singular value decomposition-based construction method for Toeplitz structure measurement matrix. First, it decomposes the Toeplitz matrix by using singular value decomposition algorithm, then it enhances the independence of column vectors of the matrix by optimising its nonzero singular values, so as to improve the reconstruction performance. Simulation results showed that compared with the non-optimised Toeplitz structure measurement matrix and the frequently used Gauss random matrix, the signal reconstruction accuracy gained significant improvement when using the optimized Toeplitz structure measurement matrix to carry out compressed sensing on signals.

KeywordsCompressed sensingMeasurement matrixToeplitz structureSingular value decompositionSignal reconstruction

收稿日期：2014-12-10。國家自然科學基金項目(61271261)；重慶市科委自然科學基金項目(CSTC2012jjA40048)。趙輝，副教授，主研領域：現代信號與圖像處理，空間光通信及光信息處理。金勝杰，碩士生。

中圖分類號TP301

文獻標識碼A

DOI:10.3969/j.issn.1000-386x.2016.06.044