淺析學習支架的應用

●白元偉　汪國荃

?

淺析學習支架的應用

●白元偉汪國荃

一、構建情境式教學

數學是開發人的邏輯思維能力的學科，但在初中數學課堂上，很多學生認為數學枯燥乏味，體味不到邏輯思維的樂趣。為了讓學生主動參與到數學課堂學習中，教師應通過創設適當的情境，激發學生的好奇心和求知欲，促使學生愿意自己去思考問題、解決問題，從而達到對知識的建構，感受做邏輯體操的快樂。

如，筆者在教學《圓》一課時，引導學生聯系生活中車輪等圓形物體形狀設想，討論車輪為什么要造成圓形。請學生想象騎著三角形、四邊形車輪騎車的情形，學生就會興奮起來，紛紛說：“不能！這樣的輪子無法滾動。”筆者接著再問：“那就造成鴨蛋的形狀吧！行嗎？”學生開始感覺茫然，繼而大笑起來：“若是這樣，車子會忽高忽低的。”教師繼續追問：“為什么造成圓形不會忽高忽低呢？”學生又一次活躍起來，紛紛議論，最終找到了答案——“因為圓形車輪上的點到軸心的距離處處相等”。這樣自然而然地得到了圓的定義，收到了很好的教學效果。這樣的教學方式，能夠讓學生在很自然的學習情境中掌握數學知識，能夠取得較好的教學效果。所以，教學時創建情境非常重要，這是“支架式”教學中的一個非常重要的環節。

二、培養探究意識

在教學活動中，教師要重視對問題的設計，通過引導學生，把抽象的數學知識與實際內容聯系起來，使學生的再認識轉化為一個學習過程，培養探究問題的意識。通過學習支架的幫助，學生可以切身體驗到數學思想產生的過程，從而對數學問題的理解變得更加準確、深刻。

如，學生在完成了“在△ABC中，∠B=25°，AD是BC邊上的高，并且AD2= BD·DC，求∠BCA的度數”的求解后，筆者繼續設計如下問題，激發學生的探究意識。出示圖1，要求學生判斷正誤，并說明理由。

圖1

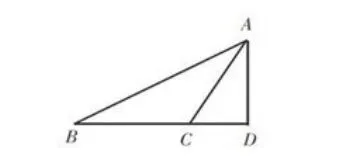
圖2

∵AD是BC邊上的高

∴∠ADB=∠ADC=90°

又∵AD2=BD·DC

∴BD∶AD=AD∶DC。

所以，△ABD∽△CAD，

故∠BCA=90°-25°=65°。

憑借已有經驗，學生很容易發現解題的不足：圖1中D點在BC邊上，只有當△ABC是銳角三角形的時候成立。要得到正確解答，還應考慮什么問題？是D點的位置，還是△ABC的分類問題？筆者設計出一系列疑問，學生在好奇心的驅動下，熱烈討論、歸納，他們發現點D的位置可以在邊BC上，也可以在BC的延長線上（當△ABC為鈍角三角形時），如圖2，此時，可解得∠BCA=115°。通過不斷引導學生思考，創建學習支架，學生思考開始有條理性，他們學會了如何將問題進行分類，如何一步步分析探究，自主學習能力不斷增強。

三、形成網絡體系

數學知識具有一定的結構性，它不是封閉的“知識體系”，而是相互聯系、動態活動的一個系統。教學過程中，教師要注意引導學生把所學的知識和實際應用結合起來，尋找知識間的相互聯系，逐步形成縱向和橫向的知識網絡體系，擴充知識結構，逐漸培養學生構建學習支架及應用學習支架的意識和能力，提高知識的應用水平和效率。

如，已知關于x為變量的一元二次方程x2+2（m-1）x+3m2-11=0有實數根，問：是否存在實數m，使方程的兩根x1、 x2滿足若存在，求出方程的兩根倒數和；若不存在，請說明理由。學生解答時出現了“”的值是“”或“”的錯誤，其原因是學生對一元二次方程概念的理解不到位，在解題時，沒有考慮一元二次方程有實數根的條件，即根的判別式Δ≥0這個條件。在教學中，筆者結合學生解題中的錯誤，引導他們梳理鏈接以前學習的一元二次方程的概念，讓學生認識到，涉及一元二次方程概念的問題時要注意的知識點。他們不僅要了解概念，還要了解根與系數的關系。

學習支架促使學生經歷了一些更更為深刻的思維過程，有助于學生對知識結構，特別是隱性知識體系的感悟與理解。

（作者單位：丹江口市石鼓鎮初級中學）

責任編輯嚴芳