剛架拱橋的極限承載力研究
■ 謝江平(福建省高速公路有限責任公司三明管理分公司,三明 365000)
?
剛架拱橋的極限承載力研究
■謝江平
(福建省高速公路有限責任公司三明管理分公司,三明365000)
摘要本文基于極限承載力分析的基本理論,以福建省尤溪縣坪寨大橋為工程背景,采用ANSYS建立有限元模型,在同時考慮幾何非線性、材料非線性及混凝土開裂特性的條件下分析極限承載力,并對剛架拱橋的破壞形式進行全過程研究。結果表明,剛架拱橋的極限承載力是以穩定控制為主,其破壞形式屬于第二類彈塑性失穩破壞,安全儲備較低,耐超載能力較差。
關鍵詞剛架拱橋極限承載力幾何非線性材料非線性
1 引言
剛架拱橋是在我國傳統的雙曲拱橋、桁架拱橋的基礎上結合斜腿剛構的特點發展演變而來的一種橋型,屬于有推力的高次超靜定結構,其受力兼有拱與梁式剛架的特性,從力學性能和經濟性上都較傳統的梁式和拱式結構為優[1]。隨著計算理論的完善、施工工法的進步以及計算機輔助設計技術的應用,剛架拱橋不僅在跨徑上有所突破,而且在橋型上也發展出了新的形式。
目前,綜合考慮結構幾何、材料非線性影響的彈塑性分析理論被廣泛運用于拱橋結構極限承載力分析[2-6],計算出的臨界荷載能較真實地反映結構的承載能力,但關于剛架拱橋的極限承載力系統性研究還是空白,因此,對剛架拱橋的極限承載力進行研究具有重要的現實意義。
2 有限元模型建立及若干問題處理
2.1工程背景
本文以福建省尤溪縣坪寨大橋為工程背景,采用ANSYS軟件建立有限元分析模型。坪寨大橋全橋總長210.72米,共分三跨,跨徑布置為63.625m+63.6m+ 63.625m,橋梁全寬12m,其中主車道9m,兩側人行道各寬1.5m,兩側欄桿各寬0.25m,設計荷載為汽車-20、掛車-100,矢跨比為1/8,正交直橋。
2.2有限元模型
鋼筋混凝土模型采用整體式模型即將鋼筋彌散于整個單元中,把鋼筋混凝土單元視為一個綜合的整體單元,全橋共劃分Solid65單元3928個,Solid45單元3150個,共有節點16373個,建立的有限元模型如圖1所示。

圖1 剛架拱橋有限元模型
2.3若干問題處理
為了提高計算速度和減小分析的復雜程度,本文提出若干假設,對模型進行了必要的簡化:
(1)忽略連拱效應,取其中一跨模型進行分析,減少了模型的單元總數和分析的復雜程度。
(2)邊界條件的模擬:忽略橋墩與橋臺的位移,并以相應的約束代替橋墩與橋臺的作用,其中拱腿與斜撐均為固結,弦桿約束豎向和橫橋向的位移。
(3)混凝土的本構關系采用E.Hongnestad曲線;鋼筋的本構關系采用理想剛塑性模型。
(4)采用恒截+全橋均布荷載(工況1)、恒截+半橋均布荷載(工況2)、恒截+半側均布荷載(工況3)三種加載工況,并且根據等代荷載法將集中荷載換算成全橋均布面荷載,計算出各工況的初始設計活荷載集度為:工況1=4.26kN/m2;工況2=8.51kN/m2;工況3=8.51kN/m2。
3 剛架拱橋的極限承載力分析
3.1雙重非線性分析
同時考慮結構的材料非線性和幾何非線性因素,并考慮混凝土的開裂特性,通過荷載增量法和迭代法相結合的方法求解結構的極限承載力。分析中考慮了恒載和活荷載的作用,其中活荷載按初始活荷載逐級增加。在三種荷載工況作用下,拱頂截面的活荷載系數-位移曲線如圖2~4所示:
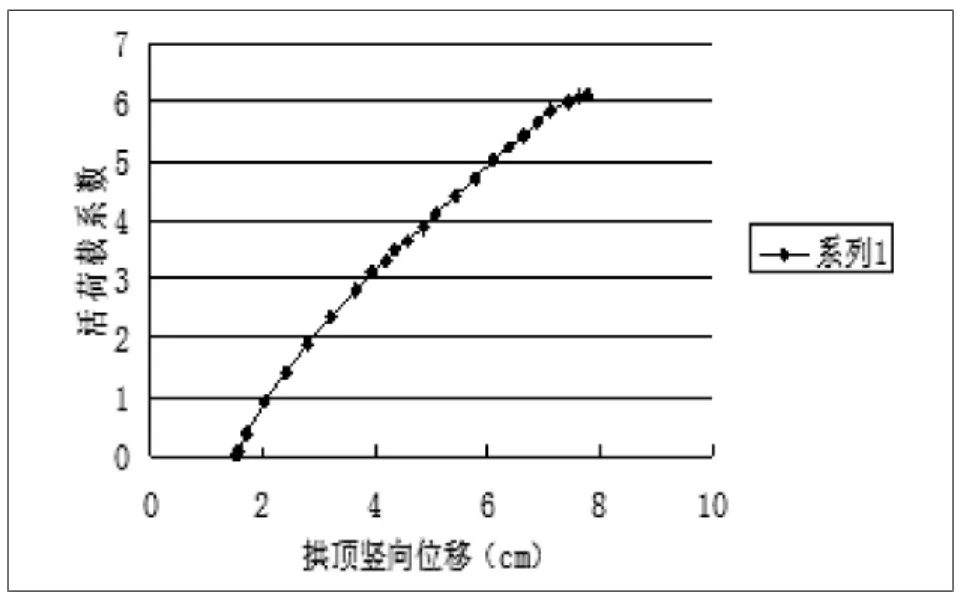
圖2 工況1作用下拱頂荷載-位移曲線
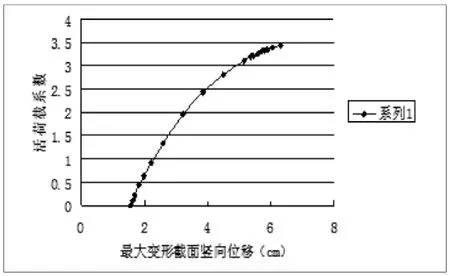
圖3 工況2作用下拱頂荷載-位移曲線

圖4 工況3作用下拱頂荷載-位移曲線
三種荷載工況下計算所得結構極限活荷載系數分別為λ1=6.15,λ2=3.440,λ3=3.580。
結果表明:一般拱橋的失穩破壞是發生面內反對稱失穩,而剛架拱橋在橫向偏載作用下橫向穩定性較差,由此可見剛架拱橋橫向聯系的重要性。
3.2剛架拱橋破壞的全過程研究
一般來說,第二類彈塑性失穩發生于下列兩種情況的交叉影響:(1)在荷載逐漸增加的過程中,結構的位移隨之逐漸增大,當在施加微小增量荷載時,結構即發生大幅度變形而不能使用;(2)在加載過程中,某些桿件由于超過屈服應力而退出工作,導致結構剛度減小,直到退化為幾何可變體系。因此,在變形漸大、構件應力漸增,發生局部屈服桿件數目不斷增多的聯合作用下,最終導致結構整體失穩。
3.2.1荷載工況1作用下結構破壞的全過程研究
當活荷載系數達到6.21時,拱橋發生第二類失穩破壞,即此時荷載達到穩定極限荷載值,相對應的最大撓度發生在拱頂(L/2拱)處,其值為7.775cm。模擬全過程結果如下:當活荷載系數值為1.896時,最大撓度發生在拱頂,位移值為2.799cm,各構件均處于彈性狀態,相對而言,拱頂周圍、主拱腿特別是大節點附近以及拱腳附近,應力較大,但均未達到屈服強度;在橫系梁與剛架拱片交接處存在明顯的應力集中現象。隨著荷載的增大,跨中橋面板最先進入塑性,大節點附近的主拱腿下緣隨后也進入塑性階段;隨著荷載的繼續增大,跨中橋面板的塑性向兩側發展,大節點的主拱腿附近下緣的塑性也向兩側及上緣發展,當達到極限荷載時,跨中橋面板塑性區進一步擴大,在很小的荷載增量作用下結構就發生較大變形,導致結構坍塌。圖5為結構破壞時全橋的裂縫發展情況。
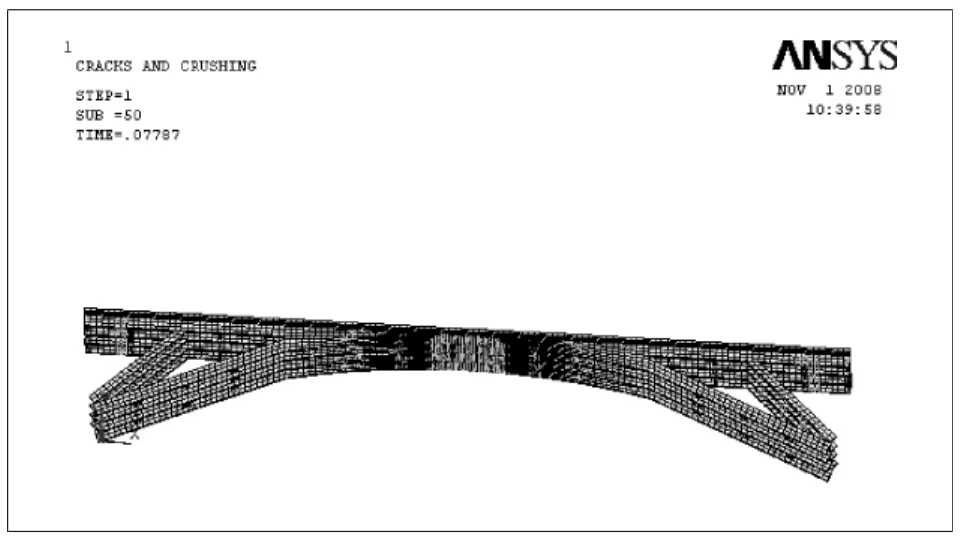
圖5 工況1作用下結構破壞時裂縫發展情況
3.2.2荷載工況2作用下結構破壞的全過程研究
本工況模擬拱橋塞車時的不利狀況。當活荷載系數達到3.440時,拱橋發生全橋面內反對稱失穩破壞。破壞時由于加載的另一側主梁下緣的混凝土應力最大,發生壓潰,全橋變形很快增大,全橋面內反對稱失穩破壞。豎向的最大變形發生在加載一側大節點與拱頂之間的截面上,最大變形值達到6.313cm。模擬全過程結果如下:在荷載作用的初期階段,加載的另一側位于跨中與大節點之間的主梁下緣應力、橫系梁(特別是加載的另一側)與剛架拱片的連接處應力最大;隨著荷載的繼續增大,未加載一側的主梁下緣的應力最先達到屈服強度,進入塑性,而另一側主梁的應力應變仍然非常小,荷載的繼續增大使得位于未加載一側的位于跨中與大節點之間的主梁下緣的混凝土被壓潰,在很小荷載作用下,結構變形增長很快,最后發生全橋面內反對稱失穩破壞。圖6為結構破壞時全橋的裂縫發展情況。

圖6 工況2作用下結構破壞時裂縫發展情況

圖7 工況3作用下結構破壞時裂縫發展情況
3.2.3荷載工況3作用下結構破壞的全過程研究
本工況模擬拱橋塞車時的不利狀況。在半側均布活荷載作用下,當活荷載系數達到3.580時拱橋發生面外失穩破壞,相對應的最大撓度發生在加載側跨中橋面板處,其值為9.336cm。模擬全過程結果如下:加載的全過程,加載側的最外側一剛架拱片受力相比其它拱片都是最大的,離加載側越遠的剛架拱片應力就越小。隨著荷載的增加,跨中加載側最外沿橋面板達到屈服強度,進入塑性狀態,并隨著荷載的增加向周圍發展,隨后靠近加載側的最外沿的剛架拱片的大節點附近也進入塑性階段,而離其越遠的拱片受力就越小,甚至處在彈性工作階段,正是這種應力分布狀況導致結構破壞時,加載側的最外沿的剛架拱片跨中橋面板的混凝土被壓潰,然后整跨結構向側傾方向歪扭,發生橫向面外失穩破壞。圖7為結構破壞時全橋的裂縫發展情況。
綜合三種荷載工況作用下結構的破壞全過程研究可以看出:此類較大跨度的鋼筋混凝土剛架拱橋,具體的破壞形式與活荷載作用形式有很大關系。總的來說,這類拱橋的破壞形式屬于第二類彈塑性失穩破壞,而且破壞前有一定的征兆,如塑性區的開展等。
3.3背景橋梁的穩定安全系數
一般拱橋的破壞形式為第二類彈塑性失穩破壞,即結構整體失穩破壞之前,局部己經發生強度破壞,而且穩定破壞更具嚴重性,故對于合理的結構設計來說,要求結構的強度破壞早于穩定破壞出現。這就要求拱橋安全系數的最低容許值應該大于強度問題的安全儲備。
按照《公路橋涵鋼結構及木結構設計規范》的容許應力計算時,安全系數是K>1.70。因此,拱橋穩定安全系數的最低容許值不應該低于1.70,背景橋梁穩定安全系數略大于按容許應力計算的安全系數容許值。
4 結論
本章對背景橋梁進行了線彈性穩定分析和第二類穩定性分析,并對拱橋極限承力的三種分析方法作了分析比較;文章著重在考慮雙重非線性因素影響下,對該結構的破壞過程和破壞形式進行全過程研究。通過分析研究,得出以下結論:
(1)剛架拱橋的橫向穩定性較差,主拱腿易發生局部失穩現象。當橫向聯系不足時,橫橋向偏載的作用容易產生橫橋向面外失穩破壞。
(2)對于剛架拱橋,破壞形式屬于第二類彈塑性失穩破壞,破壞前有一定的征兆,如塑性區的開展等。
(3)經承載力驗算,背景橋梁基本滿足設計荷載的安全性要求,但耐超載能力較差。
參考文獻
[1]姚玲森.橋梁工程.北京:人民交通出版社,1985.
[2]張建民,鄭皆連,肖汝誠.鋼管混凝土拱橋的極限承載力分析.中南公路工程,2004.
[3]張建民,肖汝誠.巫峽長江大橋極限承載能力分析.公路交通科技,2004,21(2):37-40.
[4]程進,江見鯨.拱橋結構極限承載力的研究現狀與發展.公路交通科技.2002,19(4):57-59.
[5]金偉良.鋼筋混凝土拱橋的極限承載力.浙江大學學報.1997,31 (4):449-461.
[6]李松,強士中,唐英.鋼筋混凝土拱橋極限承載力的參數研究.西南交通大學學報,2006,42(3):293-298.

