基于k-means聚類和BP神經網絡組合模型的用電負荷預測
黃 磊,陳 浩,衣喬木,陶亞龍
(1.上海新能凱博實業有限公司,上海 201210;2. 復旦大學計算機科學技術學院,上海 201203;3. 網絡信息安全審計與監控教育部工程研究中心,上海 200203)
基于k-means聚類和BP神經網絡組合模型的用電負荷預測
黃磊1,陳浩2,3,衣喬木1,陶亞龍1
(1.上海新能凱博實業有限公司,上海201210;2. 復旦大學計算機科學技術學院,上海201203;3. 網絡信息安全審計與監控教育部工程研究中心,上海200203)
摘要:電能資源不能存儲,節約電能的一個重要前提就是精準預測用電負荷。由于居民的用電負荷受多方面因素的影響(如天氣),使得用電負荷曲線為高度非線性曲線,但用電負荷的曲線又具有周期性,對于建立這種高度非線性函數并具有一定的周期性的預測模型,神經網絡是一種非常合適的方法。針對現有的電力數據,并參考了現有的方法,提出了k-means聚類和BP神經網絡組合模型的預測方法來預測用電負荷,通過與單獨使用BP網絡預測的結果進行對比,認為使用k-means聚類和BP網絡的組合模型方法進行用電負荷預測,可獲得較高精度。
關鍵詞:用電負荷;天氣;k-means聚類;BP網絡
電力是現代工業發展的根本,也是我國的重要資源。為了更好地利用電能,上海市從2012年7月1日起,實施居民階梯電價,其目的是為了促進居民合理用電,節約用電。由于我國的智能電網的發展技術相對于歐美、日本要滯后許多,導致了我國多次的用電供需失衡。國家為了解決供電量不足的問題,鼓勵各地的發電廠大力發電,同時,也導致了很多地區用電量過剩,對電力資源造成了極大的浪費。因此,用電量預測已經成為了電力部門的一個重要組成部分,尋找準確科學的預測方法是當前的首要任務。
用電負荷預測并不是一個新穎話題,該理論研究開始于20世紀80年代,到目前為止,已有30多年的歷史。在此期間,有許多的理論和方法被提出,甚至有些已經被實踐,應用到實際中去,可是,效果并不盡人意。不同的預測方法都有一定的局限性,至今,還沒有一個預測方法是普適的、是絕對的最優解。雖然用電負荷的預測方法有很多,但從大方向來說,可將其分為傳統的預測方法和經典預測方法[1-2]。無論哪種方法,都已其明顯的缺點。
常用的傳統預測的方法有相似日預測法和卡爾曼濾波理論預測法。其缺點在于難以對噪聲的特性經行估算。
常用的經典預測方法有時間序列法和回歸分析法[3]。時間序列法的缺點是他只注重數據的擬合,沒有充分的考慮影響負荷變化的原因有哪些。回歸分析法的缺點是在使用時需要實現假定函數的基本形式,并且也不能真實的反映出負荷與影響因素之間的關系[4]。
近些年來,隨著人工智能的興起和不斷發展,在很多領域中得到了廣泛的應用。其中,人工神經網絡具有非線性特性和較強的學習和歸納能力,同時可以充分考慮影響負荷變化的外部因素,從某種程度上,可以克服以上預測方法的不足。正是因為這樣,神經網絡在用電負荷預測的研究中,廣受親睞。由于數據量之大,單純的用神經網絡可能達不到理想效果,在建立神經網絡之前,有必要對數據進行處理。在本文,使用k-means聚類方法,對數據進行歸來,然后再建立BP網絡預測模型,對用電負荷進行預測。
1數據處理及分析
1.1實驗數據來源及處理
本論文的所用的用電負荷數據是上海浦東2013年1月1日至2013年12月31日的真實數據,來源于2013年數據來自浦東電力局。由于2013年的原始數據記錄信息不完整、數據記錄錯誤等原因以及數據采集的所造成的錯誤,造成一部分用戶沒有完整的365天的用電信息和一部分用戶用電量為負值的情況,無法進行統計;因此,有必要對原始數據進行篩選和預處理操作。將沒有完整2013年365天數據記錄的居民用戶和用電量為負值的居民用戶剔除,最后得到了5 036戶居民用電數據。為方便觀察,將5 036戶居民2013年1月1日至2013年12月31日的用電總量擬合成折線圖,如圖1所示。
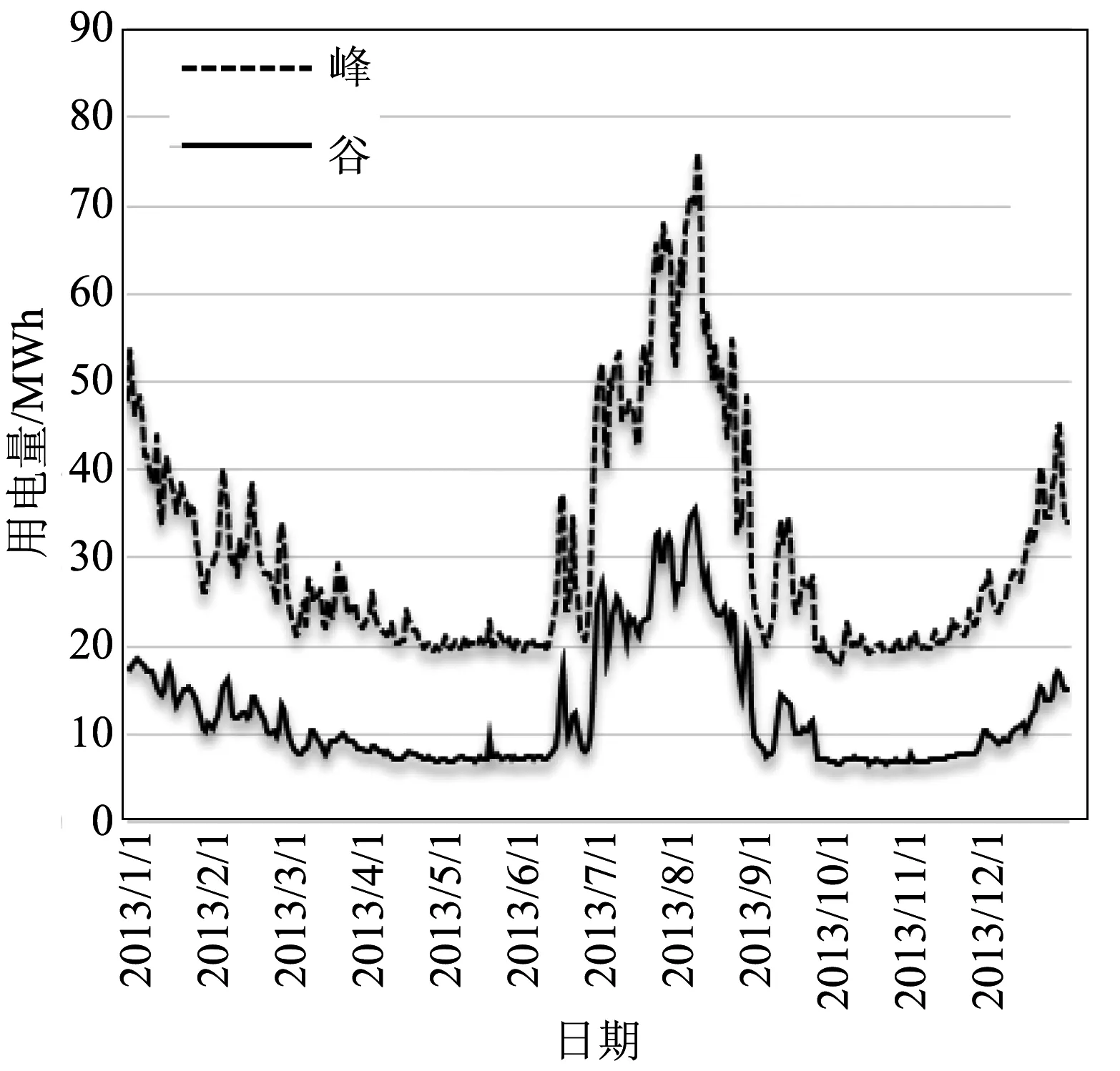
圖1 居民用電量
此外,由于居民用電負荷還與環境因素有關,比如溫度。本文也是重點考慮溫度對用電負荷的影響,所以,還要獲取2013年1月1日至2013年12月31日的天氣數據。本文所使用的天氣數據,是來自于上海浦東國際機場的所使用的天氣數據。
1.2實驗數據分析
由圖1可以看出,用電量在7月至9月為最大,而且波動也較大,1月和12月次之,4月至6月和10月至11月,用電量最小,而且也相對穩定。其原因也不難理解,由于7月至9月處于高溫時段,制冷設備會大量使用,1月和12月為最冷時段,供熱設備會大量使用,所以,會消耗更多的電量,導致用電量最大。而4月至6月,10月至11月時,在上海溫度比較適宜,大功率的制冷供熱設備較少使用,所以其用電量為最少。從以上的結論也可以看出,溫度高或者溫度低時,用電量會增大,這一結論也符合我們的常識。
此外,用電負荷曲線為光滑連續曲線,且日用電負荷也會呈現一定的周期性,所以,前一天的用電負荷,對預測當日的用電負荷具有一定的參考意義[5]。
2K-means聚類和BP神經網絡在用電負荷預測中的應用
2.1聚類分析
在數據挖掘領域中,聚類方法有多種,例如:K-means、k-中心、層次聚類、基于密度的聚類等等。由于K-means算法簡潔、快速、聚類結果比較理想,因此,K-means聚類方法也得到了廣泛的應用,本文也是采用的是K-means聚類。
K-means是典型的劃分聚類方法。將數據集D劃分成K個類。需要定義簇的代表:形心。從幾何概念上來講,簇的中心點就是它的形心,而在這里,形心可以有更多的定義方式,不僅僅是中心點,還包括了均值等。評估簇的質量可以用誤差平方和,它的定義如下:
(1)
式中E——的數據集所有對象的誤差的平方和;
p——空間上給定數據對象的點;
dist(x,y)——空間上點x到點y的歐幾里得距離。
接下來,要討論的是k是如何取值的。找到合適的k值,并非一件容易的事情,k的取值,對聚類的結果有著不同的影響。通常,找出正確的簇數依賴于數據集分布。在這里,采用肘方法,來確定k的取值[5,6]。
肘方法是基于如下觀察:增加簇的數有助于降低每個簇的簇內方差之和。這是因為有更多的簇可以捕獲更細的數據對象簇,簇中對象之間更為相似。因此,一種選擇正確的簇數的啟發方式是,使用簇內方差和關于簇數的曲線拐點。
2.2聚類過程及結果
在本文,我們根據每個用戶每個月的用電總量,進行聚類,這樣可以得到5 603*12的二維向量,根據上述論述的肘方法,得知k為3時,為最佳簇數。將每個用戶,按每月用電總量進行分類,分為三類:低用電量用戶、中用電量用戶、高用電量用戶。
根據以上的運算過程,可以得到用戶電量的聚類的結果,觀察簇心的分布情況如表1所示。
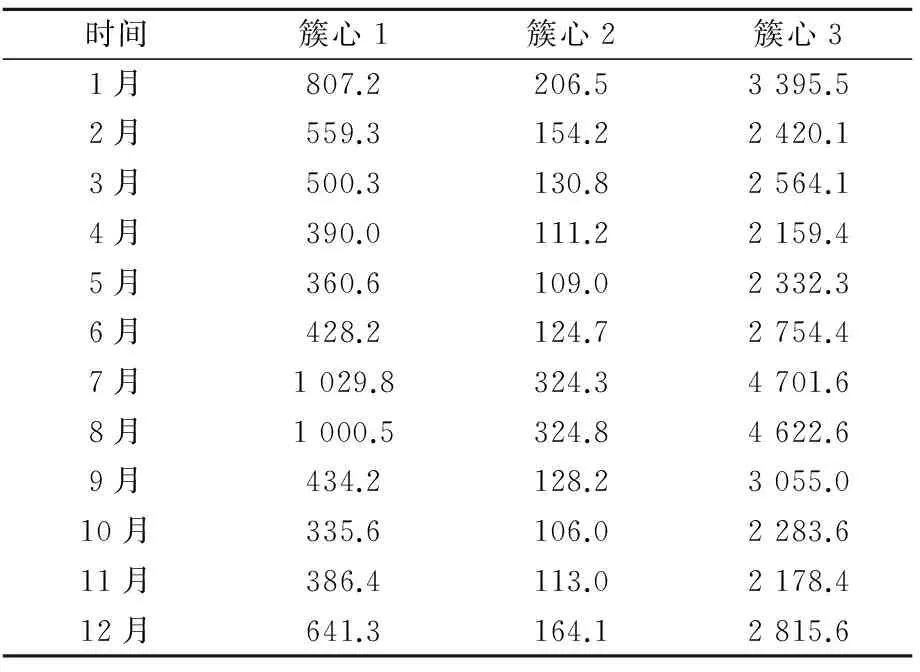
表1 用戶用電量聚類結果的簇中心 kWh
2.3BP網絡模型的建立
2.3.1BP神經網絡
人工神經網絡有很多種,如,BP神經網絡,徑向基神經網絡,遞歸網絡等。人工神經網絡提供了普遍而使用的方法。對于建立高度分線性的模型函數提供了一種非常健壯的方法。在眾多的神經網絡當中,由于BP網絡,非線性映射能力,自學習、自適應和容錯性強的特點,使得BP神經網絡得到了廣泛的應用。其結構見圖2。
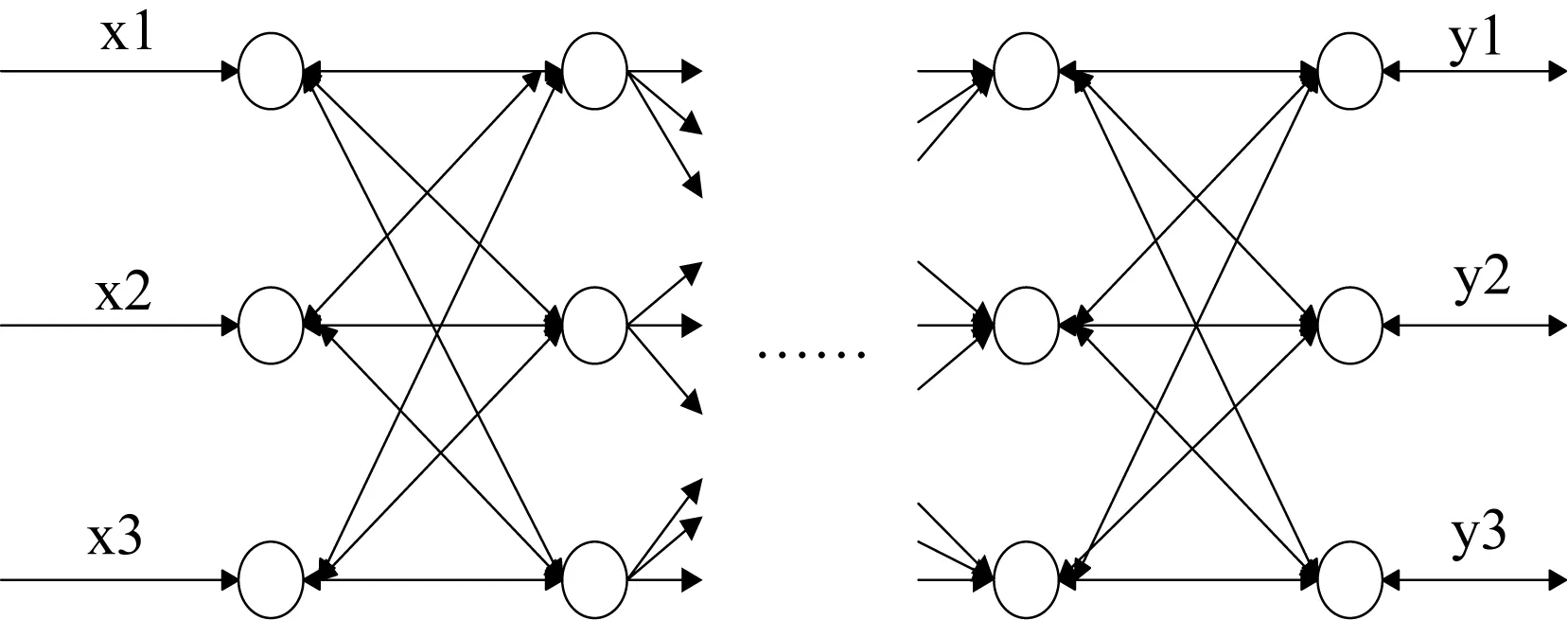
圖2 BP網絡結構
2.3.2輸入/輸出向量設計
輸入向量就是一天峰時用電總量的真實值、谷時用電總量的真實值及當天的最高氣溫和最低氣溫。因此輸入向量就是一個8維向量(前一日峰時用電量,前一日谷時用電量,前一日用電總量,當日峰時用電量,當日谷時用電量,當日用電總量,最高氣溫,最低氣溫)。
顯而易見,目標向量就是當天的峰時用電量和谷時用電量,(當日峰時用電量,當日谷時用電量)[7]。
由于輸入/輸出向量的值比較大,也比較分散,而且數量級差異也較大,預測起來會產生很大的誤差,因此還需要對輸入/輸出向量進行歸一化處理,由于輸入/輸出向量的每列的數值相差很大,所以,需要單獨對每一列歸一化,使每列數值處在[0,1]范圍之間,然后再重新組合成輸入/輸出向量矩陣。測試后的結果,要進行反歸一化。歸一化的方法有很多,這里采用如下公式[8]:
(2)
2.3.3BP網絡設計及訓練
由于本論文的用電量預測輸入向量是一個8維向量,根據Kolmogorov定理可知,中間隱含層的神經元可以取10。而輸出向量有2個,所以輸出層中的神經元應該有2個。在本文用matalb來實現該過程,網絡中間層的神經元傳遞函數采用S型正切函數tansig,輸出層中的神經元傳遞函數采用S型對數函數logsig。這是因為函數的輸出位于區間[0,1]中,正好滿足網絡輸出的要求[9-11]。
利用以下代碼在Matlab上創建一個滿足上述要求的BP網絡:
net=newff(minmax(sd),[8,2],{'tansig',logsig},'traingdm');
其中,變量minmax(sd) 用于規定輸入向量的最大值和最小值,traingdm表示設定網絡訓練函數為traingdm,它采用Levenberg-Marquardt算法進行網絡學習。
網絡設計好之后,還要進行網絡訓練,網絡經過訓練后才可以用于用電量預測的實際應用(見表2)。

表2 參數訓練
訓練代碼如下:
net.trainParam.lr= 0.05; %學習速率
net.trainParam.epochs= 10000; %訓練次數
net.trainParam.goal= 1e-3; %訓練目標
3實驗結果
3.1BP網絡預測結果
訓練好的模型還需要進行大量的測試才可以判斷是否可以投入實際應用。利用以上方法,分別將三類用戶按照上述方法建立模型,并且也分別得出了三類用戶用電量的預測結果,將所得的三類用戶用電量的預測結果,進行匯總,可得到以下結果。
單獨使用BP神經網絡預測所得到的結果以及相對誤差絕對值和分布情況(見圖3、圖4)。
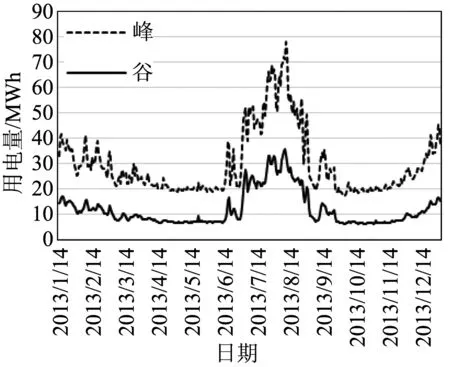
圖3 BP網絡預測結果
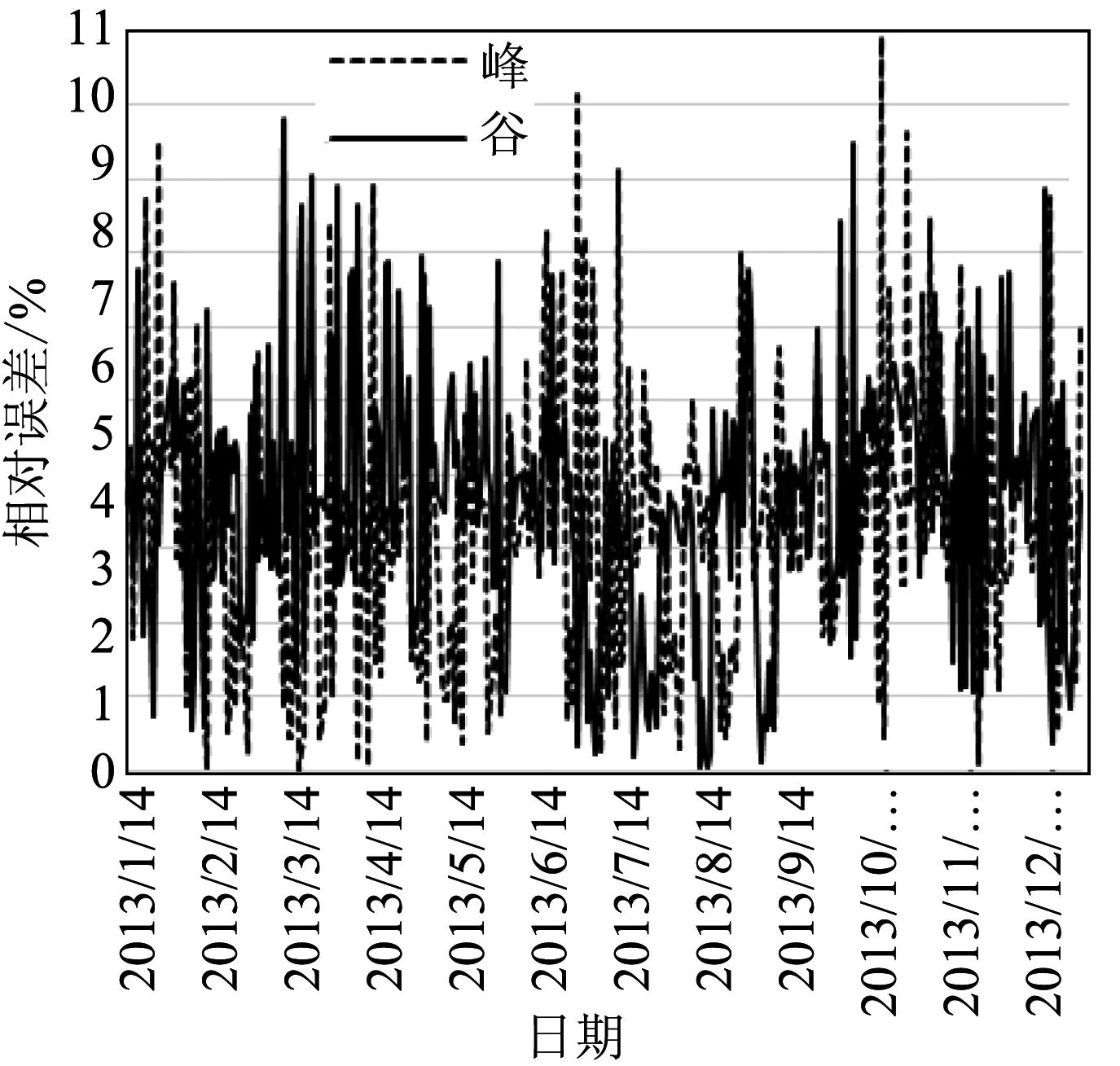
圖4 BP網絡預測結果相對誤差值
3.2k-means聚類和BP網絡組合的預測結果
基于k-means和BP網絡組合的預測結果如圖5所示。
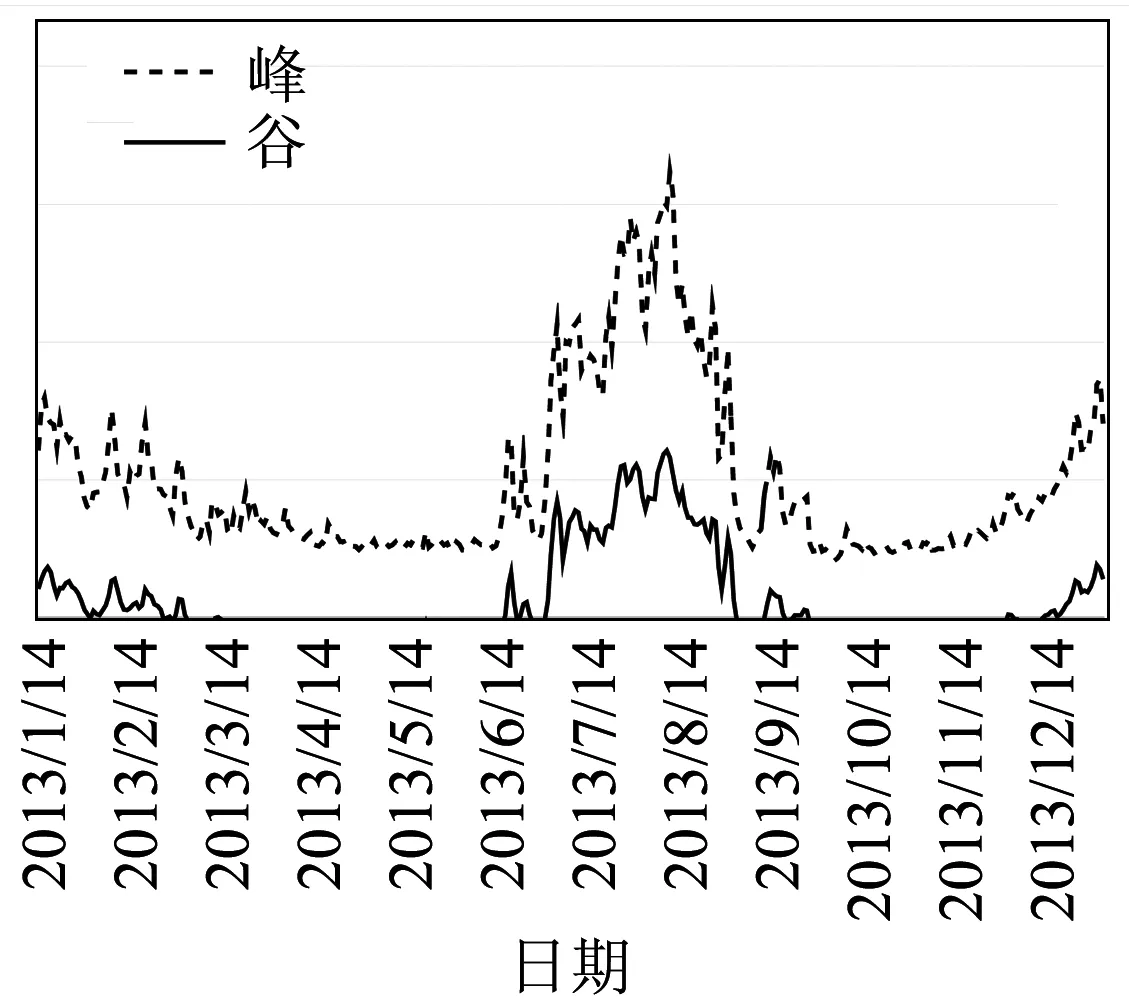
圖5 基于k-means和BP網絡組合的預測結果
將誤差值除以用電量的真實值,可得到相對誤差絕對值,繪出曲線如圖6所示。
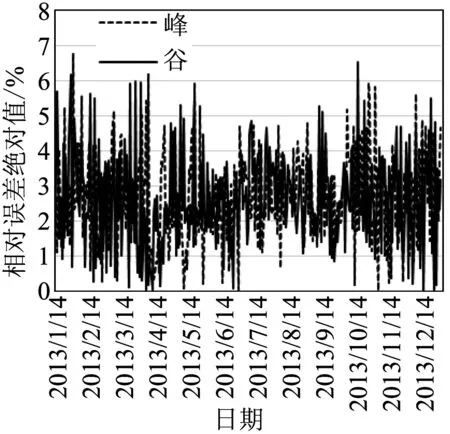
圖6 基于k-means和BP網絡組合的預測結果相對誤差絕對值
3.3兩組預測結果的比較與分析
基于上面的結果,對不同預測方法進行了比較,見表3。

表3 不同預測方法的比較
(3)
其中,MAPE為平均絕對值百分比誤差。
從表3可以看出,k-means和BP網絡組合的方法明星好于BP神經網絡的預測方法。
4結語
本文演示了基于K-means和BP神經網絡組合模型對用電量的預測。通過本文的實驗可以看出,通過K-means和BP網絡的組合方法對用電量的預測,可以獲得較高的精度,而且還可以有效克服對用電量影響比較大的因素(如:溫度)的影響。結論具有實際意義,可為電力部門的日發電需求提供一定的依據。
參考文獻:
[1]張慶新,崔展博,馬睿,等.基于k-means聚類與徑向基神經(RBF)網絡的電力系統日負荷預測.科學技術與工程,2013,13(34):10177-10181.
ZHANGQing-xin,CUIZhan-bo,MARui,etal.Dailyloadforecastingofindustrialenterprisepowersystembasedonk-meansclusteringandRBFneuralnetwork[J].ScienceTechnologyandEngineering,2013 .13( 34):1017 7-10181.
[2]錢虹,阮大兵,黃正潤.電力系統超短期負荷預測算法及應用. 上海電力學院學報,2013,29(1):9-12.
QIANHong,RUANDa-bing,HUANGZheng-run.Ultra-short-termloadforecastingalgorithmandapplication[J].JournalofShanghaiUniversityofElectricPower, 2013,29(1):9-12.
[3]孫紅英.改進的BP神經網絡方法在用電量預測中的應用.西安文理學院學報,2007,10(2):88-91.
SUNHong-ying.ApplicationofimprovedBPneuralnetworkinforecastingelectricityrequirement[J].JournalofXi′anUniversityofArts&Science:NaturalScienceEdition,2007,10(2):88-91.
[4]朱雨晨,加瑪力汗水,娜仁花.基于BP神經網絡的電力系統短期負荷預測.黑龍江電力,2012,34(6):439-441,445.
ZHUYu-chen,GamalihanoKumash,Narenhua.Short-termloadforecastingbasedonBPneuralnetworkforelectricpowersystem[J].HeilongjiangElectricPower, 2012,34(6):439-441,445.
[5]WANHe.Deepneuralnetworkbasedloadforecast.COMPUTERMODELLING&NEWTECHNOLOGIES,2014,18(3):258-262.
[6]熊永勝.基于BP神經網絡的電力系統短期負荷預測.成都大學學報,2012,31(2):167-169.
XIONGYong-sheng.Short-termloadforecastingofpowersystembasedonBPneuralnetwork[J].JournalofChengduUniversity(NaturalScience), 2012,31(2):167-169.
[7]陸柳敏.基于Matlab的電力系統中長期負荷預測及應用.廣西電力,2012,35(6):26-28.
LULiu-min.MediumandlongtermloadforecastingandapplicationbasedonMatlab[J].GuangxiElectricPower,2012,35(6):26-28.
[8]祝燕萍,方鴿飛.基于動態自適應神經網絡和人體舒適度的短期負荷預測.電力系統保護與控制,2012,40(1):56-61.
ZHUYan-ping,FANGGe-fei.Short-termforecastingbasedondynamicadaptiveartificialneuralnetworkandhumanbodyamenityindicator[J].PowerSystemProtectionandControl,2012,40 (1):56-61.
[9]劉耀年,王衛,楊冬峰.基于模糊劃分聚類的中長期用點預測.東北電力學院學報,2004,24(4):39-42.
LIUYao-nian,WANGWei,YANGDong-feng.Mid-longtermelectriccapacityforecastingbasedonfuzzyclustertheory[J].JournalofNortheastChinaInstituteofElectricPowerEngineering, 2004,24(4):39-42.
[10]馬光文,王黎,唐明,等.人工神經網絡在用電預測中的應用.四川大學學報,2000,32(2):25-27.
MAGuang-wen,WANGLi,TANGMing,etal.Powerdemandforecastingbyneuralnetworkmodel[J].JournalofSichuanUniversity(EngineeringScienceEdition), 2000,32(2):25-27.
[11]趙錫平,宋岱,張國慶,等.山東省氣溫與最大負荷和用電量的關聯性分析.電網技術,2004,28(17):37- 40.
ZHAOXi-ping,SONGDai,ZHANGGuo-qing,etal.Researchoncorrelativityamongairtemperature,maximumloadandpowerconsumptioninshandongpowergrid[J].PowerSystemTechnology,2004,28(17):37-40.
(本文編輯:趙艷粉)
Load Forecast Based on Hybrid Model with k-Means Clustering and BP Neural Network
HUANG Lei1, CHEN Hao2,3, YI Qiao-mu1, TAO Ya-long1
(1.XinnengKaiboIndustrialCo.,Ltd.,Shanghai201210,China;2.SchoolofComputerScience,FudanUniversity,Shanghai201203,China;3.EngineeringResearchCenterofCyberSecurityAuditingandMonitoring,MinistryofEducation,Shanghai200203,China)
Abstract:The development and popularity of the smart grid makes us more aware of the value of power energy resources. As we all konw, electricity cannot be stored, so accurate forecast is of great significance for saving electricity. Because the resident power consumption is affected by many factors, such as weather, the electricity load curve is highly nonlinear, but periodic, and neural network is a very suitable method for establishing the forecasting model. Based on the existing electric power data and methods, this paper presents a hybrid model with the k-means clustering and BP neural network to forecast the electricity load. Compared with the results only using BP network to forecast electricity load, it is concluded that the hybrid method can achieve high precision in forecasting the electricity load.
Key words:electricity load;weather;k-means clustering;BP neural network
DOI:10.11973/dlyny201601012
作者簡介:黃磊(1965),助理工程師,從事電力電子技術,電力用戶側需求研究。
中圖分類號:TP399
文獻標志碼:A
文章編號:2095-1256(2016)01-0056-05
收稿日期:2015-11-13

