刀傾全展成準雙曲面齒輪的切齒設計

王　星, 方宗德, 王　磊, 李聲晉

(1.西北工業大學 機電學院, 西安 710072; 2.西安交通大學 高端制造裝備協同創新中心, 西安 710054)

刀傾全展成準雙曲面齒輪的切齒設計

王星1, 方宗德1, 王磊2, 李聲晉1

(1.西北工業大學 機電學院, 西安 710072; 2.西安交通大學 高端制造裝備協同創新中心, 西安 710054)

摘要:為提高準雙曲面齒輪的嚙合性能，對刀傾全展成(HGT)準雙曲面齒輪進行切齒設計研究．以局部綜合法(Local Synthesis)為基礎，并依據格里森準雙曲面齒輪的加工原理，得到滿足一定嚙合性能的加工參數，并采用該參數對齒輪副進行輪齒接觸分析(TCA)． 從齒面印痕和傳動誤差曲線可以看出，齒輪副重合度大，傳動平穩，可通過調整局部控制參數來改變齒輪的嚙合性能，驗證了切齒設計的正確性．該方法可通過對設計參考點及其領域內的嚙合條件進行預控，達到對齒面嚙合質量的控制．關鍵詞: HGT加工方法；準雙曲面齒輪；局部綜合法；加工參數；輪齒接觸分析

準雙曲面齒輪被廣泛用作汽車主減速器齒輪,由于小、大輪之間偏置距的存在,可有效增加汽車的平穩性或者越野性,因此,對準雙曲面齒輪進行研究更具有普遍意義．

國內外一些學者對對準雙曲面齒輪的設計、制造和加工進行了研究[1-5]．Kawasaki等[6]分別采用解析和實驗方法研究了大型擺線齒螺旋錐齒輪的齒面接觸模式．Park等[7]提出了一種準雙曲面齒輪表面磨損的近似計算方法．Mohammadpour等[8]對不同準雙曲面齒輪在大負荷下的非牛頓混合彈流動力學進行了分析．Takeda等[9]對準雙曲面齒輪的嚙合性能進行了分析,并通過實驗測量了傳動誤差．Simon[10]針對面滾式準雙曲面齒輪提出了一種優化方法,用來系統地定義刀盤參數和機床加工參數．

準雙曲面齒輪的嚙合質量需要通過正確的切齒參數的調整來實現．基于局部綜合法[11-12]的切齒設計可以滿足以上要求．楊宏斌等[13]研究了基于局部綜合法的刀傾半展成(HFT)法加工高齒準雙曲面齒輪的切齒參數設計,從文獻中可以看出,該方法很難控制接觸跡線為直線,導致齒輪副對安裝誤差的敏感性較大．刀傾全展成(HGT)方法,大輪采用雙面刀盤展成加工,雖然加工效率沒有成形法高,但是齒面曲率特性好,能更好地控制齒輪的嚙合性能,因此,本文對HGT準雙曲面齒輪進行研究．方宗德等[14]通過局部綜合法對HGT準雙曲面齒輪的優化切齒設計進行了前期理論探索,并沒有通過算例給以定量計算和驗證．本文作者曾對HGT準雙曲面齒輪進行了工作齒面的理論推導,并進行了TCA計算[15],然而該工作無法對齒輪的嚙合性能進行預控．

綜上所述,在已有螺旋錐齒輪主動設計技術中,沒有將齒面的高性能設計與加工結合起來．本文結合展成法和刀傾法,提出基于局部綜合法對HGT準雙曲面齒輪進行加工參數設計研究,實現對齒面的主動設計,并通過TCA定量分析驗證了參數推導的正確性．

1局部綜合法基本原理簡介

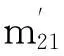
2大輪加工參數及參考點的確定

2.1確定大輪加工參數

大輪切齒參數設計坐標系如圖1所示．圖1中,O2F、O2P、O2和O2R分別為面錐頂點、節錐頂點、交叉點和根錐頂點,b2為大輪齒寬,Am為大輪中點錐距,ZG和ZR分別為節錐頂點到設計交叉點的距離和節錐頂點到根錐頂點的距離,H2和V2分別為大輪刀盤的水平刀位和垂直刀位,Sr2和q2分別為徑向刀位和角向刀位,RG2為刀盤半徑,β2為大輪中點螺旋角．Oc2是大輪機床中心,也是平面產形輪的中心,Og是刀盤中心．σ2、σr2和θr2分別為大輪的節錐角、根錐角和齒根角．X2為大輪的旋轉軸,坐標系O2-X2Y2Z2為大輪加工坐標系,φ2為大輪加工轉角;X與大輪節錐線重合,坐標系O2p-XY為大輪旋轉投影面坐標系．

給定垂直輪位Em2=0,根據圖1,大輪加工參數為

式中:Xg2、Xb2和Cr2分別是軸向輪位、床位和滾比．至此,大輪的加工參數已完全確定．

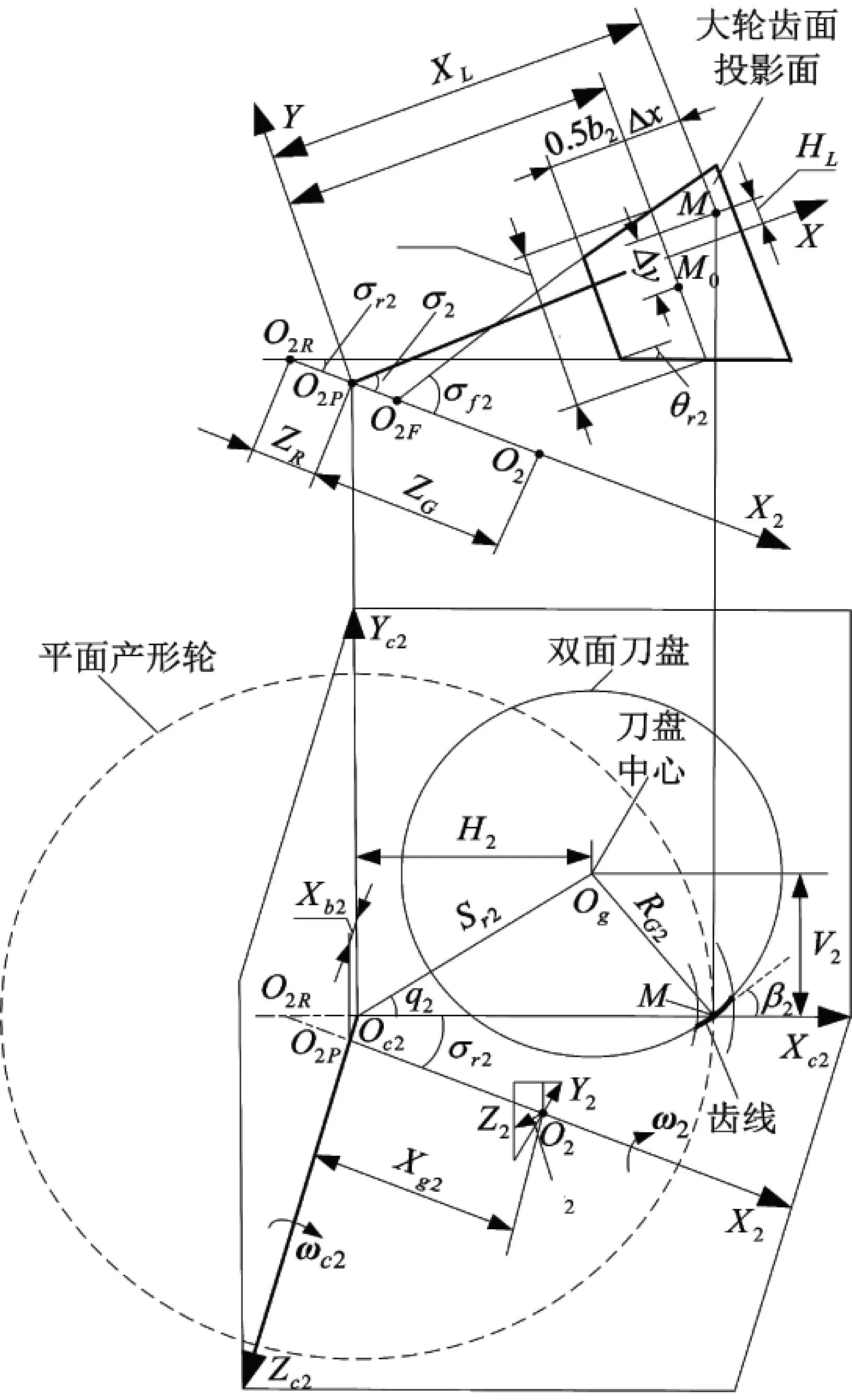
圖1　大輪切齒參數設計坐標系

2.2確定參考點

如圖1中所示,hmf和hmr分別是大輪中點齒頂高和中點齒根高,所以,中點全齒高

M0是齒面中點，

M是要確定的參考點,Δx和Δy分別是M點在齒寬和齒高方向距齒面中點M0的距離,M點的位置由參數XL和HL決定：

因此,調整Δx和Δy的值,即可按需要確定參考點M的位置,同時,根據XL和HL,可計算出M點處的大輪刀盤轉角、搖臺轉角和刀盤錐面參數．

2.3參考點大輪的主方向和主曲率

根據文獻[1]中線接觸計算公式,由大輪刀盤切削面的主曲率和主方向,求出大輪齒面上參考點的主曲率和主方向．

大輪刀盤切削錐面圖見文獻[15]中圖1(a)所示．其位矢和單位法矢如下：

式中: rc2、Sg、α2和θg分別表示大輪內刀刀尖半徑、刀盤錐面參數、刀盤齒形角和刀盤轉角．

所以,大輪刀盤切削錐面的主方向表示為

(1)

(2)

相應的大輪刀盤切削錐面的主曲率表示為

(3)

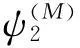
(4)

(5)

式中:rc2、nc2分別為機床坐標系中大輪齒面參考點M處的位矢和法矢;Mc2g為刀盤坐標系到機床坐標系的轉換矩陣;Lc2g為Mc2g的旋轉矩陣．Mc2g可表示如下:

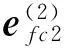
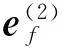
式中: M2c2為機床坐標系到大輪坐標系的轉換矩陣,L2c2為M2c2的旋轉矩陣．M2c2可表示如下:

(6)

(7)

式中: Mh2為大輪坐標系到嚙合坐標系的轉換矩陣,Lh2為Mh2的旋轉矩陣．Mh2可表示如下:

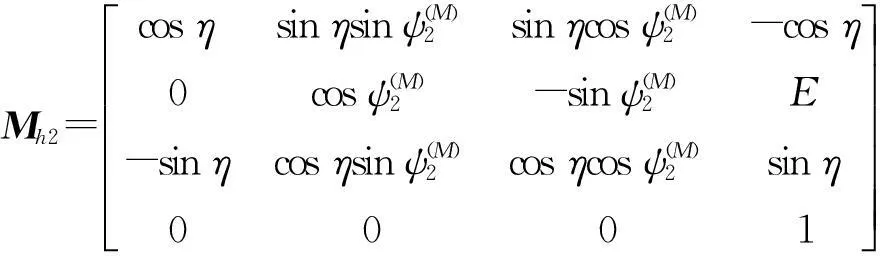
式中:η、E分別為大、小輪的軸夾角和偏置距．

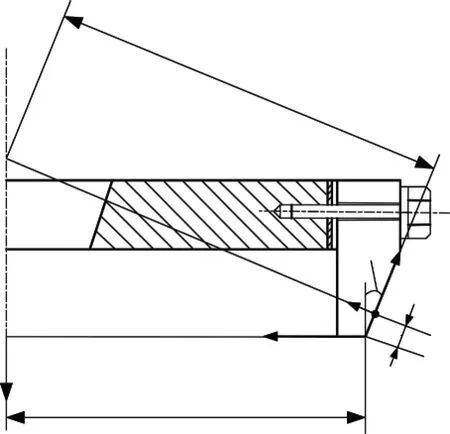
3確定小輪加工參數

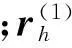
(a) 外刀

(b) 內刀

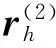
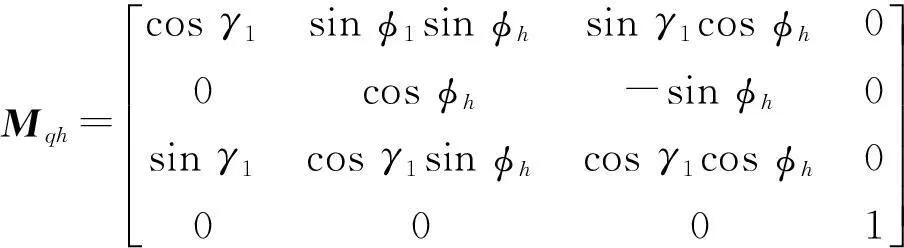
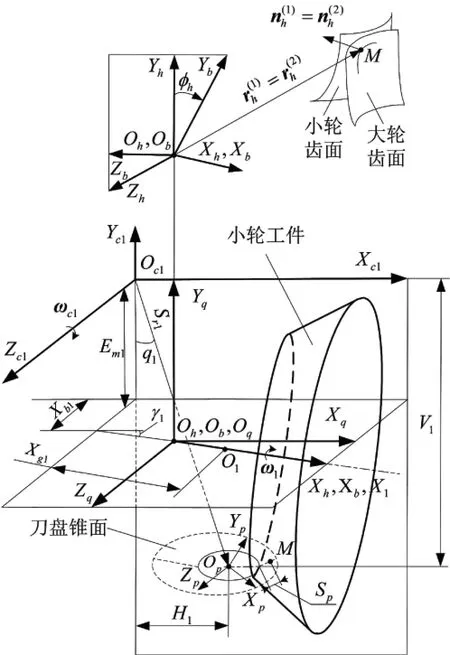
圖3　小輪切齒參數設計坐標系

小輪和產形輪的嚙合方程為

(8)

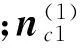
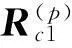
所以,根據圖3,小輪的水平刀位H1、垂直刀位V1、床位Xb1、徑向刀位Sr1和角向刀位q1為

另外,小輪的刀傾角i和刀轉角j可由刀盤軸線的單位矢量

求得:

這樣,小輪的加工參數可完全確定．

4算例驗證

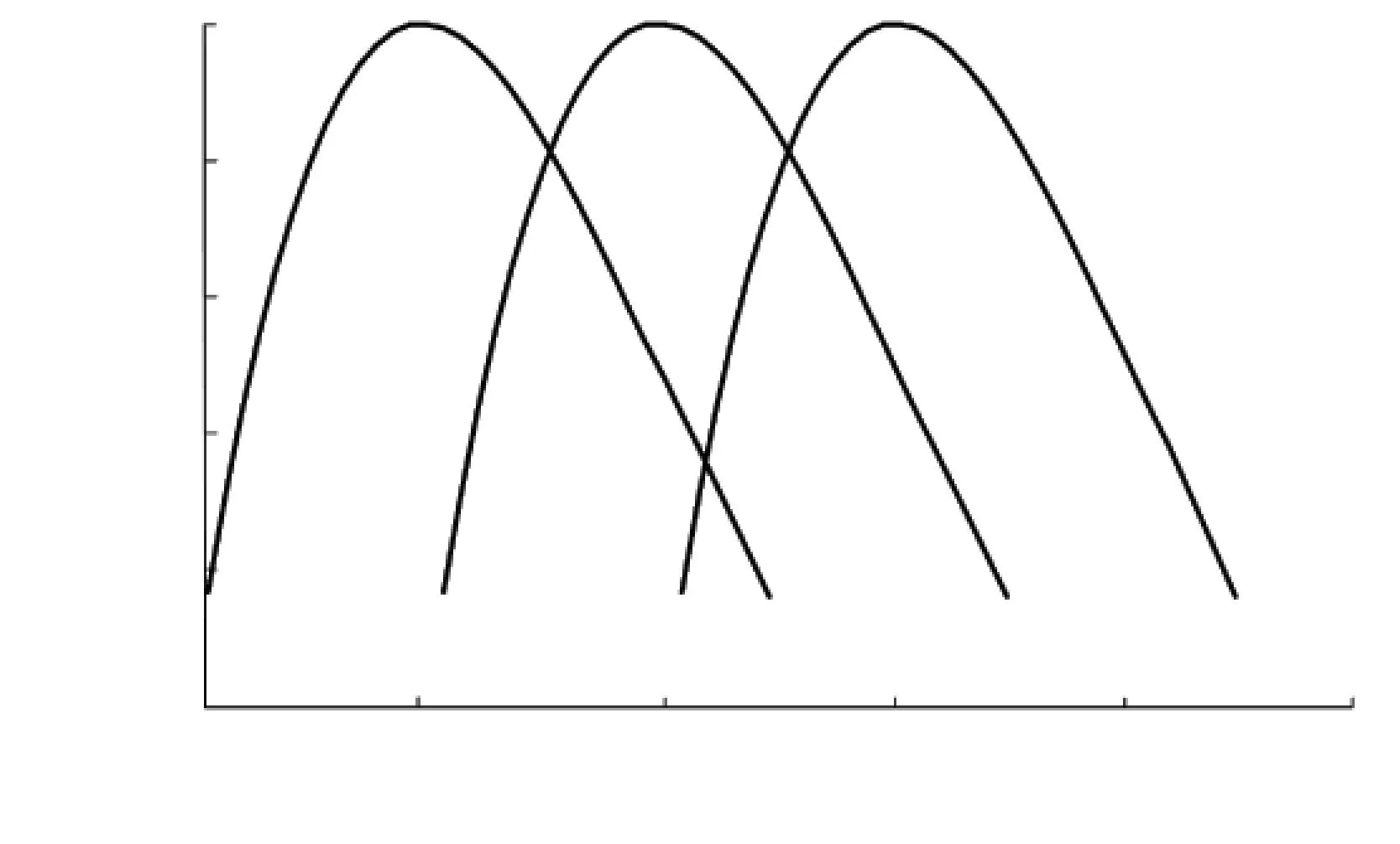
用以上方法對一對HGT準雙曲面齒輪副進行切齒參數設計,輪坯參數見表1,切齒參數見表2中算例1(小輪采用單面法加工,這里僅列出小輪凹面的加工參數),齒面方程推導見文獻[16],TCA[16]分析結果見圖4．局部控制參數為接觸跡線與齒根夾角為35°， 傳動誤差曲線斜率為-0.000 4, 瞬時接觸橢圓長軸占齒寬比例為0.3, 參考點齒寬方向控制參數Δx=3mm，參考點齒高方向控制參數Δy=2mm, 改變參考點的位置,令Δx=3,Δy=2,即令齒面印痕向大端和齒頂移動,此時大輪切齒參數不變,小輪切齒參數見表2中算例2,TCA分析結果見圖5．

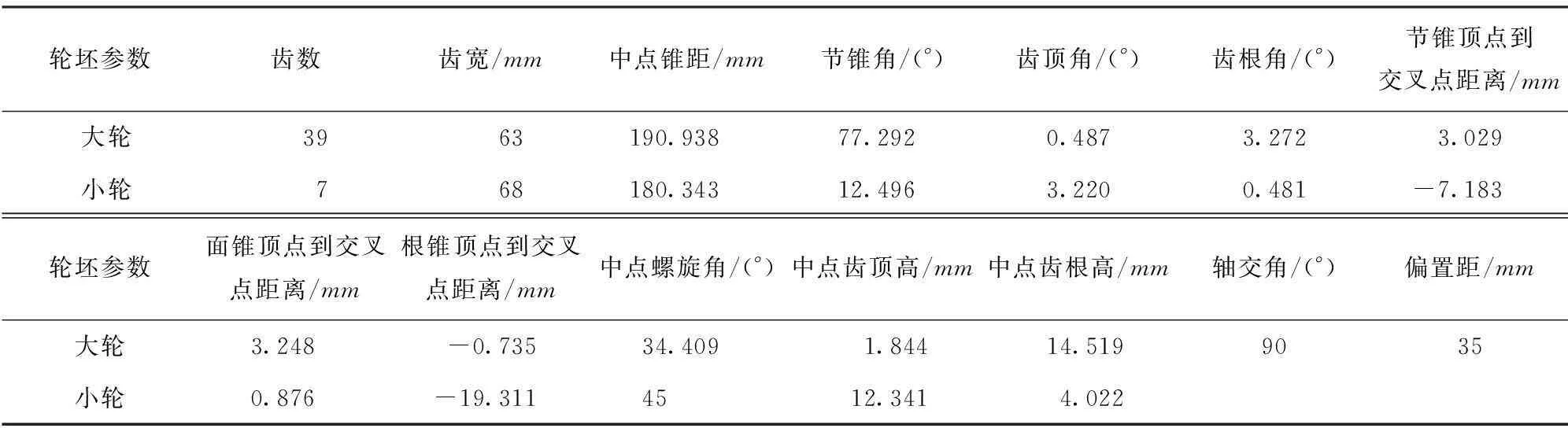
表1　輪坯參數

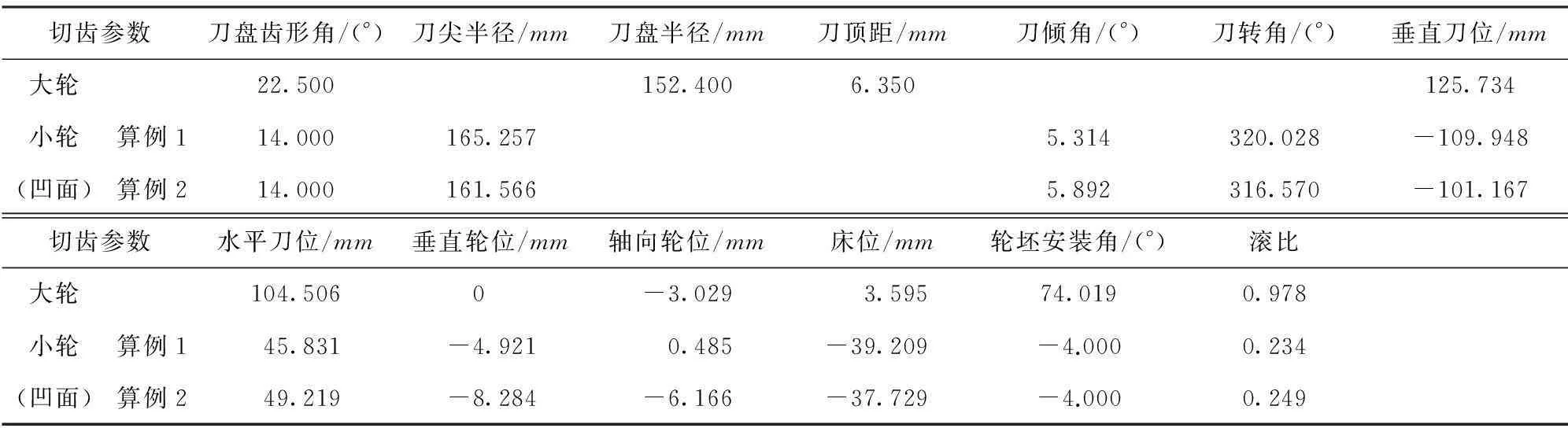
表2　切齒參數

(a) 齒面印痕

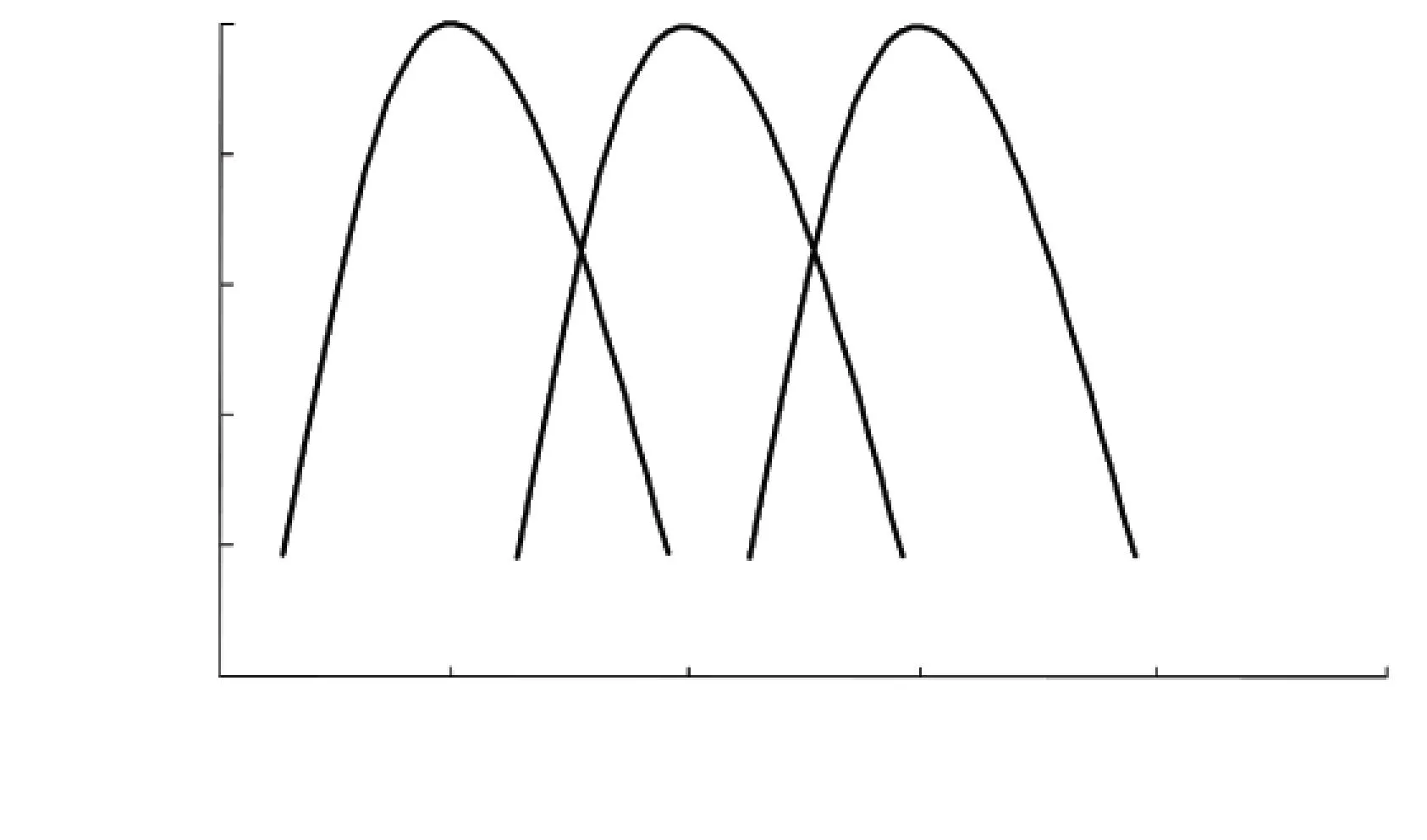
(b) 傳動誤差曲線

(a) 齒面印痕

(b) 傳動誤差曲線

由圖4可以看出,接觸跡線接近直線,可避免邊緣接觸和輪齒齒頂、齒根的應力集中;傳動誤差幅值較大,且沒有出現邊緣接觸,避免了輪齒傳動的振動與沖擊,使齒輪傳動平穩．

由圖5可知,當參考點位置改變后,齒面印痕也相應隨之改變,且接觸跡線同樣接近直線;傳動誤差對稱并且幅值較大．同理,可通過改變其他局部控制參數得到不同的切齒參數,進而得到不同的齒面印痕和傳動誤差曲線．

以上分析結果,驗證了切齒參數設計的正確性．

5結論

1)HGT準雙曲面齒輪大輪采用展成法加工,齒面曲率特性好,能有效改善齒輪的嚙合性能,這一點是成形法所不具備的;小輪采用刀傾法加工,可簡化刀具規格,使操作調整相對簡單,這一點又優于變性法．因此,本文的研究為挖掘目前常見的加工方法,或探索新的加工方法,獲得高性能的準雙曲面齒輪提供了方法和保證．

2)確定改善嚙合和切觸狀態的切齒參數是齒輪研究的主要課題,本文以局部綜合法為基礎,對HGT準雙曲面齒輪進行了切齒參數設計,通過控制參考點的一階和二階接觸參數,達到了對齒面嚙合性能的控制．該研究為高精度HGT準雙曲面齒輪的設計與加工提供了有效工具．

3)本文的設計方法保證了齒面接觸跡線為直線,可降低對安裝誤差的敏感性;且保證了接觸跡線與齒根有較小的夾角,增大了齒輪副的重合度,使齒輪運轉平穩．驗證了本文切齒設計方法的正確性．

參考文獻

[1] LITVIN F L. Gear geometry and applied theory[M]. Seccond edition. New York: Cambridge University Press, 2004:604-623.

[2] FAN Q. Tooth surface error correction for face-hobbed hypoid gears[J]. Journal of Mechanical Design, 2010, 132(1): 011004.

[3] FAN Q. Optimization of face cone element for spiral bevel and hypoid gears[J]. Journal of Mechanical Design, 2011, 133(9): 091002.

[4] SIMON V V. Advanced manufacture of spiral bevel gears on CNC hypoid generating machine[J]. Journal of Mechanical Design, 2010, 132(3): 031001.

[5] SIMON V V. Generation of hypoid gears on CNC hypoid generator[J]. Journal of Mechanical Design, 2011, 133(12): 121003.

[6] KAWASAKI K, TSUJI I. Analytical and experimental tooth contact pattern of large-sized spiral bevel gears in cyclo-palloid system[J]. Journal of Mechanical Design, 2010, 132(4): 041004.

[7] PARK D, KOLIVAND M, KAHRAMAN A. An approximate method to predict surface wear of hypoid gears using surface interpolation[J]. Mechanism and Machine Theory, 2014, 71: 64-78.

[8] MOHAMMADPOUR M, THEODOSSIADES S, RAHNEJAT H, et al. Non-Newtonian mixed elastohydrodynamics of differential hypoid gears at high loads[J]. Meccanica, 2014, 49(5): 1115-1138.

[9] TAKEDA R, KOMORI M, NISHINO T, et al. Performance analysis of generated hypoid gear based on measured tooth flank form data[J]. Mechanism and Machine Theory, 2014, 72: 1-16.

[10]SIMON V V. Optimization of face-hobbed hypoid gears[J]. Mechanism and Machine Theory, 2014, 77: 164-181.

[11]LITVIN F L, ZHANG Y. Local synthesis and tooth contact analysis of face-milled spiral bevel gears[R]. Chicago: University of Illinois, 1991:16-39.

[12]張華, 鄧效忠. 基于局部綜合的非零變位弧齒錐齒輪切齒仿真[J]. 農業機械學報,2007,38(5):204-206.

[13]楊宏斌, 范明, 周彥偉,等. 高齒準雙曲面齒輪的研究[J]. 中國機械工程,2000,11(8):897-900.

[14]方宗德,楊宏斌. 準雙曲面齒輪的優化切齒設計[J].汽車工程,1998,20(5):302-307.

[15]王星, 方宗德, 李聲晉. HGT準雙曲面齒輪傳動的輪齒接觸分析[J]. 西北工業大學學報, 2014, 32(3): 475-480.

(編輯楊波)

Machine-tool settings design for HGT hypoid gear drives

WANG Xing1, FANG Zongde1, WANG Lei2, LI Shengjin1

(1.School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China;2.Collaborative Innovation Center of High-End Manufacturing Equipment, Xi’an Jiaotong University, Xi’an 710054, China)

Abstract:To obtain high quality gear, the machine-tool settings design is studied for HGT hypoid gears. Using local synthesis method as the basis, and based on the machining principle of Gleason hypoid gear, the machine-tool settings are obtained which can satisfy certain meshing performance, and then the tooth contact analysis is done. From the contact pattern and transmission error curve we can see that the gear pairs has big coincidence degree and stable transmission, and its meshing performance can change through the adjustment of local control parameters, so the correctness of the machine-tool settings design is verified. This method can get the optimal machine-tool settings through pre-controlling the meshing condition of the design reference point, and it has a significance for designing high precision hypoid gears.

Keywords:Hypoid Generated Tilt processing method; hypoid gears; local synthesis method; machine-tool settings; tooth contact analysis

doi：10.11918/j.issn.0367-6234.2016.07.027

收稿日期:2015-03-31

基金項目:國家自然科學基金(51375384;51175423;51205310)

作者簡介:王星(1982—),女,博士研究生; 方宗德(1948—),男,教授,博士生導師

通信作者:方宗德,fauto@nwpu.edu.cn

中圖分類號:TH132.41

文獻標志碼:A

文章編號:0367-6234(2016)07-0163-06