信息不完備情況下多因素工序質量診斷方法
李金艷, 余忠華, 徐宣國
(1.浙江大學 機械工程學院, 杭州 310027; 2.江蘇科技大學 經濟與管理學院, 江蘇 鎮江 212003)
信息不完備情況下多因素工序質量診斷方法
李金艷1,2, 余忠華1, 徐宣國2
(1.浙江大學 機械工程學院, 杭州 310027; 2.江蘇科技大學 經濟與管理學院, 江蘇 鎮江 212003)
摘要:為解決信息不完備情況下的多因素工序質量診斷問題,在工藝機理分析的基礎上,提出基于貝葉斯網絡模型構建與推理的問題溯源方法. 在貝葉斯網絡結構學習過程中,利用基于評分/搜索的思想對基于工藝的預先假設結構,通過互信息參量排序降低學習復雜度. 針對生產過程中隨機因素對診斷準確性的影響問題,結合Leaky Noisy-OR模型引入隨機參量節點,對數據需求和推理進行降解優化. 以溝道磨削表面形貌質量問題的診斷為例,給出模型構建與推理程序,并驗證了所構建模型及優化方法的可行性和有效性.
關鍵詞:工序質量問題;貝葉斯網絡; 互信息;Leaky Noisy-OR模型;溝道磨削
產品的質量是關系到企業市場競爭能力的重要指標. 隨著市場競爭的日益加劇,生產模式向多品種小批量方面發展. 由于加工工藝的復雜性、監測方法的局限性以及信息的不完備,導致工序質量問題的診斷成為影響生產的瓶頸. 針對該問題國內外學者進行了大量研究,主要集中在物理解析建模和數據驅動建模兩個方面. 物理解析建模[1]是在專業技術經驗和工程知識的基礎上對制造過程進行分析[2],識別關鍵控制特征和關鍵產品特征之間的關系[3]. 數據驅動建模方法則是基于過程測量數據[4],利用多元統計分析提取數據特征的方式識別質量問題[5]. 兩者在應用方面取得了矚目成果,但均建立在工藝知識和檢測數據信息完備的前提條件下. 在部分實際生產過程中,由于工藝、設施、環境等對質量問題影響機理的模糊性和監測條件的限制,無法獲取足夠的信息建立精確的解析模型或借助統計方法進行問題診斷.
貝葉斯網絡是一種可以進行不確定知識表達和推理的方法,利用其對不確定性的推理能力,可以有效地進行多源信息表達與融合,適用于多源異類、不確定信息條件下的知識表達和推理. 目前,該方法的應用研究主要集中于可靠性、風險分析以及系統故障診斷等領域[6]. 在制造過程工序質量診斷方面,文獻[7]結合該方法針對汽輪機轉子法蘭聯接孔的加工缺陷進行了建模和推理研究,文獻[8]利用該方法建立了柔性生產線質量診斷模型,這些研究均建立在因果關系明確且結構簡單的前提下;文獻[9]針對小數據集情況通過網絡結構學習和參數學習,對某車型側圍裝配過程進行了貝葉斯網絡建模與偏差源診斷,但未考慮診斷過程中隨機因素的影響.
本文在上述研究的基礎上,以貝葉斯網絡為建模工具,首先結合工藝知識對相關影響因素和質量問題進行預先因果假設,建立初始網絡結構;然后,分別利用基于評分/搜索方法和Leaky Noisy-OR模型進行網絡結構學習和條件概率推理的降解優化;最后,以溝道磨削表面質量問題診斷為例,對所構建模型及優化方法的可行性和有效性加以驗證.
1貝葉斯網絡基本原理
1.1概念界定
貝葉斯網絡[10]是一種以網絡結構表示變量間依賴關系的概率圖模型. 在貝葉斯網絡[11]中,定性信息主要通過網絡的拓撲結構表達,定量信息則通過節點的先驗概率和條件概率表示,即B=
定義1條件獨立假設. 給定節點vi,其父節點f(vi)狀態給定后,vi條件獨立于非vi子代節點構成的任何節點集. 即若
則
定義2條件概率與鏈乘原則. 由v1,v2∈V,P(v2)>0,知
鏈式規則:V={ v1,v2,…,vn},其聯合概率可表示為
2基于工藝-工況狀態-問題的貝葉斯診斷網絡模型構建
產品一般由多個零部件組成,每個零件又由多道工序加工完成. 為了保證產品的最終加工質量,需要對每個零件的加工質量進行控制,而零件的加工質量又取決于其加工工序序列的穩定性.
在生產工藝機理明確,檢測數據信息完備且樣本量足夠的情況下,加工工序質量可利用領域知識結合數學模型表達如下[1]:
yk=Ckxk+vk.
式中:xk為質量特征向量, yk為xk的測量表征向量, xk-1為與其存在影響關系的前接工序質量特征向量, uk為本工序加工狀態向量, Ak-1、Bk、Ck為由領域知識決定的結構矩陣,wk、vk為隨機變量.
在實際生產過程中,由于工序質量問題(yk)發生的隨機性、工藝的復雜性(Ak-1、Bk、Ck)以及診斷信息(xk-1, uk)的不完備性,致使無法搜集到足夠的信息建立結構模型. 為此,需要由專家或技術人員通過對工況情景和相關參量的調查,利用經驗對搜集的質量問題證據進行分析找出根源,這個過程帶有“試錯”的理念,并缺乏系統性. 多因素工序診斷過程本質上就是從問題現象到影響因素的推理過程[7]. 本文從系統論的角度對質量問題進行建模,將質量問題的發生看作是具體加工單元中各種要素節點相互聯系作用形成的結果[12],采用適用于不確定性問題表示與推理的貝葉斯網絡作為建模工具,影響因素與質量特性指標間的因果關系及影響程度分別通過貝葉斯網絡模型的有向無環圖和條件概率表進行定性的表達和定量的評估, 概念模型如圖1可知:若將先驗知識與現有信息融合通過貝葉斯網絡可以溯源質量問題影響因素的發生情況. 此時,B=
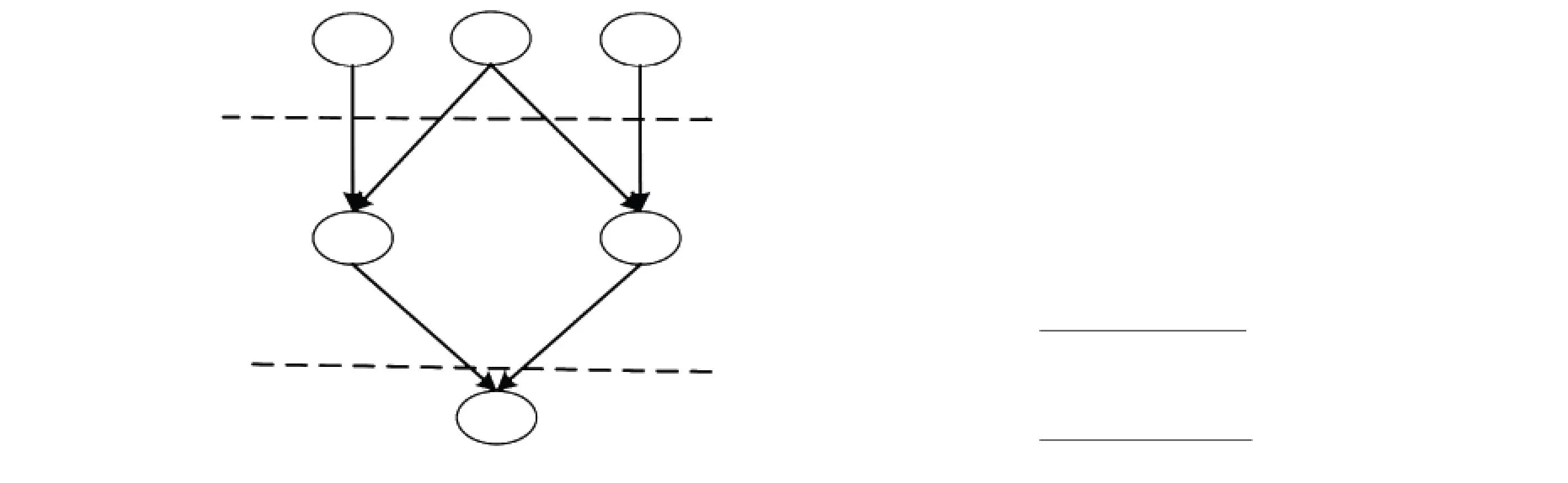
圖1 質量問題診斷的貝葉斯網絡因果機制示意
由圖2(a)所示,若將節點集S′={xk-1,uk,wk}視為一個整體,則轉化為如圖2(b)所示,此時節點xk只有一個父節點S′和一個子節點yk,同時xk的存在,不影響S′→yk的概率傳播,因此根據文獻[13],可以將節點xk刪除,直接構建S′→yk的有向邊,見圖2(c),此時S={S′,ck,vk}={xk-1,uk,wk,ck,vk},O={yk},其中ck為測量相關影響因素,其他節點含義與上同.

(a)初始結構 (b)簡化結構 (c)優化后的結構
各變量的聯合概率分布P為
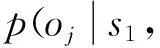
由于工藝復雜性及相關信息的模糊與不完備性,所構建的貝葉斯網絡依然無法避免節點眾多、結構模糊復雜對結構學習與條件概率推理造成的推演難度問題.
3貝葉斯網絡結構學習與條件概率推理優化
3.1結構優化
對于單工序的質量問題診斷采用質樸型貝葉斯結構,設為兩層,即影響因素層S={s1,s2,…,sn}和質量問題表征層O={o1,o2,…,om},所有節點為[0,1]二值狀態,同時滿足假設條件:1)輸入層節點之間互為獨立;2)在給定父節點情況下,條件獨立于非子代節點構成的任何節點集;3)?oj∈O,Nf(oj)≤α,其中α為某一限值. 結構學習主要是確定工序質量問題與相關影響因素之間的關聯關系,目前主要有基于搜索與評分的方法和基于依賴關系分析的方法. 針對節點較多,信息量不足,需要較多借助歷史統計信息與專家知識的情況,前者學習效率更高一些. 為此本文采用基于評分搜索的K2算法,針對一個給定的初始結構,利用互信息作為評分函數使其變量有序,逐步增加或刪減有向邊,從而確定出一個較好的網絡結構.

由量化表述信息X不確定度的信息熵:

得
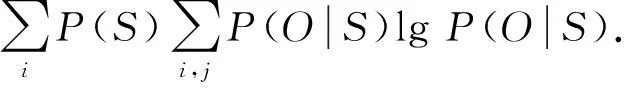

根據工藝領域知識對S與O的依賴關系進行預先假設,對I(S,O)表達的依賴或影響程度進行排序得出簡約后的因果關聯關系,結構復雜度降至m×α. 但對條件概率計算而言,若存在α個原因父節點,則需估計2α條概率,在樣本數據并不充分的情況下,獲得條件概率表中的每一項是很困難的. 此外,實際生產過程中由于wk、vk等隨機因素以及I(si,oj)<β節點的存在,即使簡約后的各si節點均處于控制穩態,O仍有可能發生異常.
3.2基于Leaky Noisy-OR的維數優化
Noisy-or gate模型是解決數據缺失問題的一種方法[14]. 在網絡結構已知,具備一定的專家知識和經驗的條件下,利用 Noisy - or gate模型可以近似確定相關節點的條件概率. Noisy-or gate模型成立的假設前提條件[15]除3.1節所提及1)、2)外,對于每一個父節點,設



由p1,p2,…,pn可以確定問題節點O的條件概率表

pL為其他節點正常時,隨機參量L導致質量問題發生概率,即


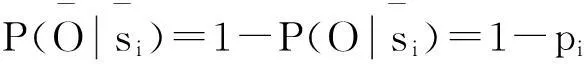
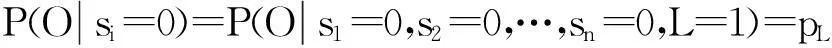
(1)
pi+pL-pi×pL.
從而得
pi=(P(O|si=1)-pL)/(1-pL) =
(P(O|si=1)-P(O|si=0)/
(1-P(O|si=0)).
(2)
質量問題發生以及各原因節點異常的概率為
(3)
(4)
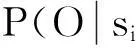
4應用
在軸承的應用過程中,套圈溝道[16]負責引導滾動體沿著軌道作軌跡運動,需要承受較大的軸向和徑向負載,是影響軸承壽命的主要環節. 目前,溝道大多采用變進給切入磨削方式,其原理是利用經圓弧砂輪修整器修整過的成形砂輪,做垂直于套圈溝道表面的切入進給,通過工件和砂輪的相對運動生成圓弧溝道. 該過程主要分為快速趨近、粗進給、細進給和光整4個階段,加工精度直接影響到軸承使用時的振動和噪聲,其中對精度影響最大的是溝道表面形貌問題,主要呈現方式有圓度誤差、表面粗糙度和波紋度誤差.
本文以608-2RS深溝球軸承的溝道磨削工序表面質量問題診斷為例論證上述建模、優化和推理過程的可行性.
4.1基本工藝
由于608-2RS深溝球軸承屬于精密軸承范疇,以內圈外徑做工藝基準,采用浮動支撐方式. 該工序基本工藝信息如下:
采用608-2RS球軸承溝道磨削. 材料為GCrl5軸承鋼,硬度為60~65 HRC. 加工設備采用3MZl43A/1型自動球軸承外圈溝道磨床,加工精度為E-D級. 砂輪尺寸規格18 mm*3.5 mm*4 mm,粒度100~125 μm,磨料為MA,陶瓷結合劑,硬度L.磨削液為5#機油. 砂輪轉速為48 000 r/min,工件轉速960 r/min.
溝道表面形貌主要涉及溝道粗磨和精磨兩個工序,影響磨削軸承溝道圓度的主要因素可歸納為前接工藝特征、物理加工環境、工藝系統狀態、執行工況以及測量等方面,具體如圖3所示.
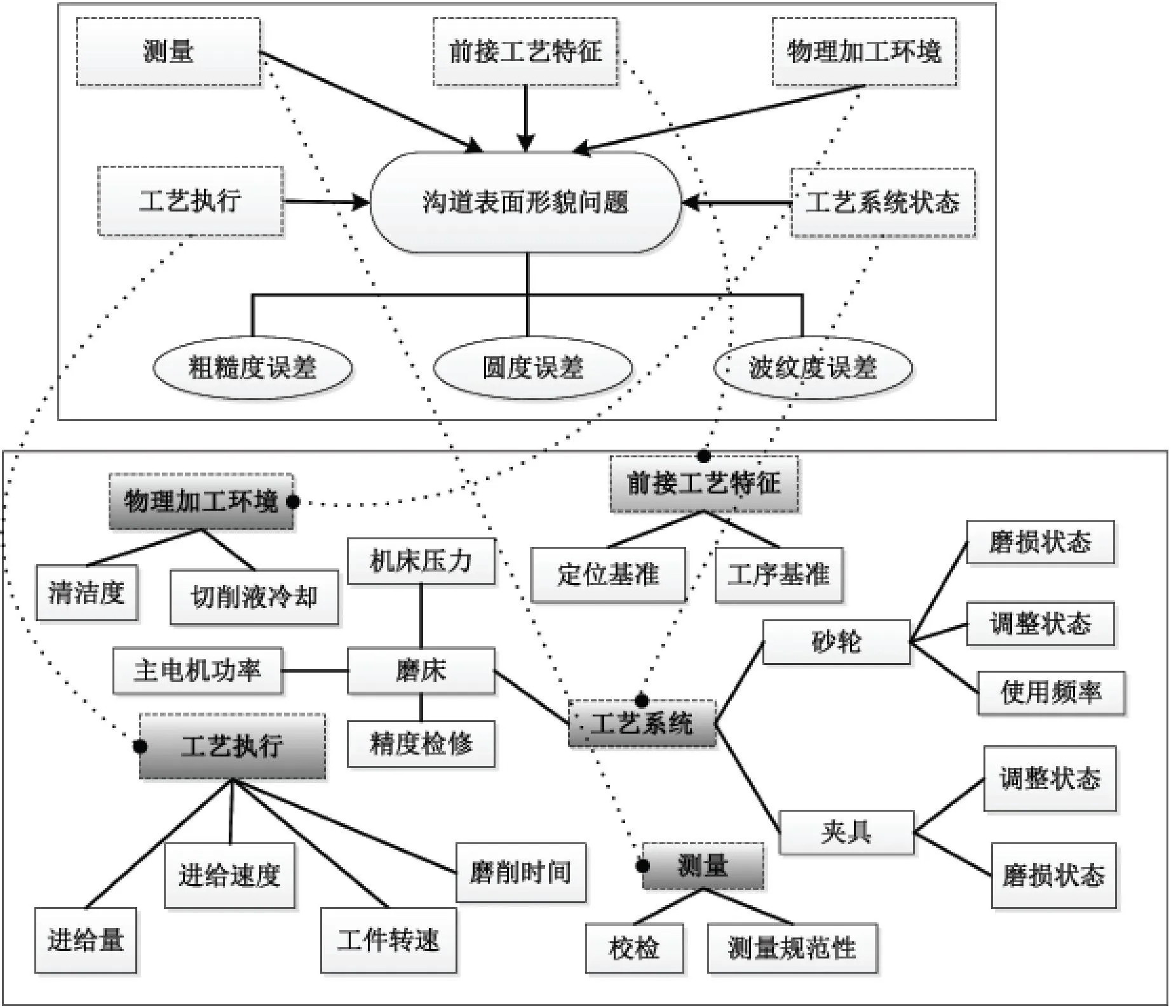
圖3 溝道表面形貌問題相關影響因素的工藝分析
4.2溝道表面形貌問題診斷
針對溝道表面形貌問題(O),在以上工藝分析的基礎上,利用魚骨圖結合頭腦風暴,進行相關影響因素節點的歸納,做出對貝葉斯網絡結構的初步假設. 以某時段圓度超差問題O2為例,具體的質量問題診斷步驟如下:
Step 1確定網絡節點集V={S,O},如表1所示,各節點狀態為二值變量:正常狀態(0)、異常狀態(1).
Step 2基于領域知識對S,O的依賴關系進行預先假設,如圖4所示.
Step 3計算圓度誤差問題節點O2與各影響因素節點之間的互信息I(si,o2),確定簡約后的圓度誤差問題O2的貝葉斯網絡拓撲結構,結果如圖5所示.
Step 4設節點參量L表示磨削過程與測量過程的隨機影響因素,結合Leaky Noisy-OR Gate模型求解圓度誤差O2的相關影響因素條件概率.
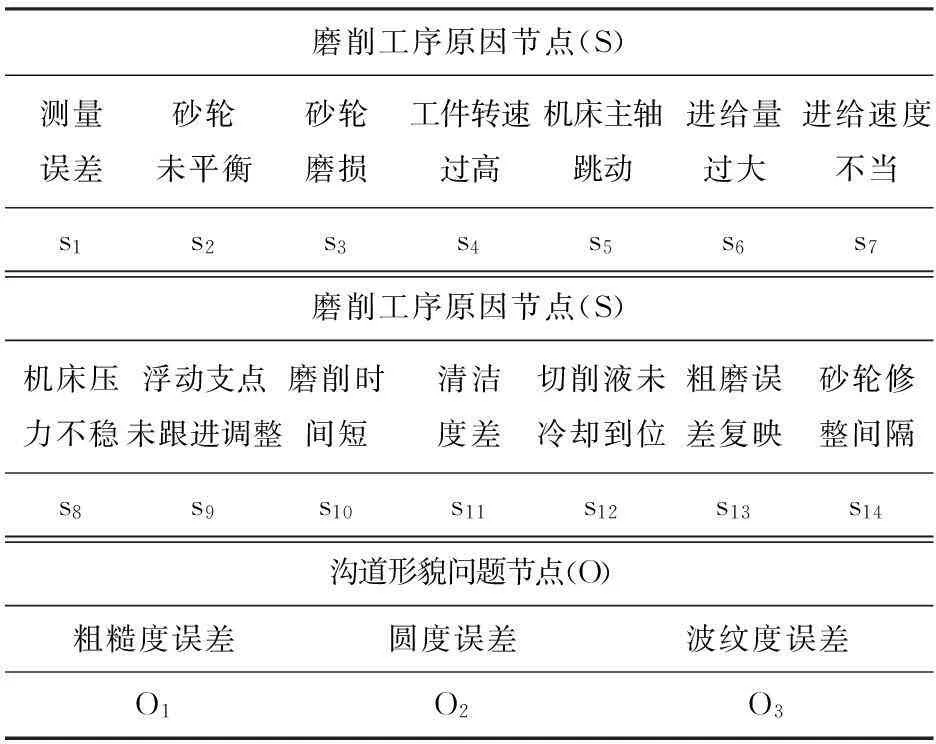
表1 診斷模型節點

圖4基于領域知識的溝道表面形貌問題的預設網絡拓撲結構

圖5 軸承溝道圓度超差問題診斷貝葉斯網絡拓撲結構
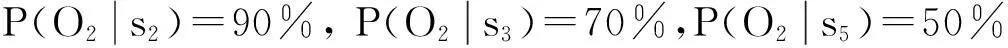
Step 5將各影響因素節點條件概率從大到小排序,初步取閾值γ≥50%作為影響因素的判定界值,結果如表2所示.

表2 主要因素診斷結果
根據表2結果,由操作人員對執行工況逐一調整排解.
Step 6如果經檢測,圓度誤差問題O2依然存在,則將所得檢測和工況信息作為新的證據并入,轉至Step 1繼續,直至問題解決.
4.3問題診斷結果討論

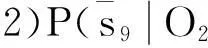

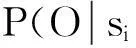
5結論
1) 本文在工藝機理分析的基礎上,針對數據信息缺失情況下的工序質量診斷問題,采用基于評分搜索的K2算法構建簡約貝葉斯網絡模型;
2)結合Leaky Noisy-OR節點模型,將生產過程中隨機因素的影響納入到推理模型,使概率推理更加接近實際的同時,簡化了估計條件概率量;
3) 利用溝道磨削表面形貌質量問題診斷對所構建模型及優化方法的可行性和有效性進行了驗證,并針對數據缺失情況與質樸貝葉斯網絡做了比較評估;
4)由于不同時刻、不同工況下各節點的先驗概率為動態參量,而本文是從靜態的角度切入進行的研究,所以在推廣應用中尚有一定的局限性,需要進一步深入分析動態貝葉斯網絡在這方面的拓展.
參考文獻
[1] SHI J J,ZHOU S Y.Quality control and improvement for multistage systems: A survey[J].IIE Transactions,2009 (41):744-753.
[2] 張磊,張志勝,周一帆,等.基于半參數回歸模型的制造過程加工誤差流建模與分析[J].機械工程學報,2013,49(15):180-185.
[3] HAN K, WANG K B. Coordination and control of batch-based multistage processes[J].Journal of Manufacturing Systems,2013 (32): 372-381.
[4] 牛青,莫蓉,萬能.基于二分法的多因素工序質量診斷算法[J].機械工程學報,2014,50(2):202-206.
[5] 王寧,徐濟超,楊劍鋒.多級制造過程關鍵質量特性識別方法[J].計算機集成制造系統,2013,19(4):888-895.
[6] WEBER P,MEDINA-O G, SIMON C, et al. Overview on Bayesian networks applications for dependability, risk analysis and maintenance areas[J]. Engineering Applications of Artificial Intelligence,2012,25(4):671-682.[7] 李麗娟,高建民,陳琨.基于Bayesian網絡的機械加工缺陷溯源方法[J].計算機集成制造系統,2010,16(7):1452-1457.
[8] 馬淑梅,黃慶,謝楠.基于貝葉斯網絡的柔性生產線質量診斷模型[J].機械設計與研究,2012,28(6):107-110.
[9] 劉銀華,金隼.基于小數據集貝葉斯網絡建模的偏差源診斷方法[J].上海交通大學學報,2012,46(5):701-705.[10]PEARL J.Probabilistic reasoning in intelligent systems: networks of plausible inference [M].San Mateo,CA: Morgan Kaufmann,1988.
[11]張連文,郭海鵬.貝葉斯引論[M].北京:科學出版社,2006.
[12]YANG L, LEE J.Bayesian belief network-based approach for diagnostics and prognostics of semiconductor manufacturing systems[J].Robotics and Computer-Integrated Manufacturing, 2012,28(1): 66-74.
[13]董曄弘,向東,龍旦風,等.基于貝葉斯網的制造工藝質量建模方法[J].計算機集成制造系統,2010,16 (12):2564-2569.
[14]ONISKO A,DRUZDZEL M J,WAYSYLUK H.Learning Bayesian network parameters from small data sets: application of Noisy-OR Gates [J].International Journal of Approximate Reasoning,2001,27(2):165-182.
[15]王華偉,周經倫,何祖玉,等.基于貝葉斯網絡的復雜系統故障診斷[J].計算機集成制造系統,2004,10(2):230-234.[16]周福章,夏新濤,周近民.滾動軸承制造工藝學[M].西安:西北工業大學出版社,1993.
[17]嚴思晗.軸承套圈溝道磨削的進給狀態參數監測及其工藝試驗研究[D].杭州:浙江大學,2006.
(編輯楊波)
Diagnosis method of multi-cause process quality under incomplete information
LI Jinyan1,2, YU Zhonghua1, XU Xuanguo2
(1.School of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China;2. School of Economics and Management, Jiangsu University of Science and Technology, Zhenjiang 212003, Jiangsu, China)
Abstract:Aiming at the problem of multi-cause process quality diagnosis under the circumstance of information losing, a method based on construction and inference of Bayesian network model is proposed. In the learning process of Bayesian network structure, the thought of score/search is adopted for the assumption structure so as to reduce the learning complexity through the mutual information parameters sorting. In view of the influence of random factors on the diagnostic accuracy, the Leaky Noisy-OR model is adopted, which simultaneously degrades the requirement quantities of data and reasoning. In the end, a problem diagnosis for channel grinding is taken as an example to verify the feasibility and effectiveness of the proposed model and optimization method.
Keywords:process quality issues; bayesian networks; mutual information; Leaky Noisy-OR model;channel grinding
doi:10.11918/j.issn.0367-6234.2016.07.014
收稿日期:2015-10-29
基金項目:國家自然科學基金 (71371088)
作者簡介:李金艷(1982—),女,博士研究生; 余忠華(1963—),男,教授,博士生導師
通信作者:余忠華, caq_221@zju.edu.cn
中圖分類號:TP202
文獻標志碼:A
文章編號:0367-6234(2016)07-0088-06

