熱障涂層活塞熱應力分析的格點型有限體積法

龔京風, 宣領寬, 周少偉, 明平劍

(1. 中國艦船研究設計中心, 武漢 430064; 2. 哈爾濱工程大學 動力與能源工程學院, 哈爾濱 150001)

熱障涂層活塞熱應力分析的格點型有限體積法

龔京風1, 宣領寬1, 周少偉1, 明平劍2

(1. 中國艦船研究設計中心, 武漢 430064; 2. 哈爾濱工程大學 動力與能源工程學院, 哈爾濱 150001)

摘要:為研究熱障涂層(thermal barrier coating, TBC)活塞熱應力問題,將二維格點型有限體積法(cell vertex FVM, CV-FVM)推廣用于三維復合材料熱力性能研究．利用交錯網格技術,通過將物性參數和待解變量分別定義在單元中心和節點上,將物性參數的空間變化引入離散過程,從而避免數值不連續問題．采用CV-FVM數值模擬普通活塞熱應力場,計算結果與ANSYS計算結果吻合良好．數值模擬TBC活塞熱應力場,分析活塞TBC區域的熱力性能,結果表明:活塞的最大溫度位于燃燒室與活塞頂面的交界區域;應力最大值位于粘結層與陶瓷層的分界面附近;周向應力對活塞的整體應力水平起主要影響．數值結果表明CV-FVM能夠作為TBC活塞熱力性能研究的數值預測工具．

關鍵詞:交錯網格技術;格點型有限體積法;熱障涂層;活塞;熱應力

熱障涂層(thermal barrier coating, TBC)活塞有助于改善內燃機的燃燒性能、排放性能、抗爆震性能等，TBC最重要的作用是為活塞基體提供熱防護，減少傳入活塞基體的熱量. 而TBC應當采用何種形式，以及TBC對于活塞熱力性能的改變是設計階段需要研究的重要問題.

建立適用于熱障涂層活塞熱力性能研究的數值方法,作為TBC活塞設計階段的預測工具,分析TBC活塞溫度場、熱應力場、熱變形具有重要意義．

目前,關于TBC活塞熱力性能的數值仿真相對較少,一般采用的是基于FEM的商用軟件．王素等[1-3]采用ADINA數值分析復合材料活塞的整體性能,指出使用陶瓷纖維梯度層可以明顯改變活塞溫度分布,緩和由于熱膨脹系數不匹配,在陶瓷纖維增強層與活塞本體交界處產生的應力,但沒有詳細討論活塞表面熱應力性能．Buyukkaya等[4-5]在活塞上表面全部涂覆TBC,采用ANSYS數值模擬其溫度場,指出普通活塞的最大溫度出現在燃燒室中心,而TBC活塞的最大溫度在燃燒室與活塞頂面交界處．Cerit等[6-7]在活塞頂面局部涂覆TBC,采用ANSYS數值模擬其溫度場及熱應力場,給出了溫度、應力在各材料交界面處的分布曲線．由于TBC活塞在基體表面有涂層材料,相對于傳統活塞數值分析,TBC活塞數值分析需要額外考慮如何劃分TBC區域網格和如何處理非均勻材料．Aboudi等[8]指出，為了獲得正確的復合材料熱應力場,在控制方程的離散過程中需要引入物性參數的空間變化．傳統的FEM賦予每一個網格單元均勻的物性參數,未考慮材料屬性的空間變化,這一處理可能導致計算結果存在人工數值不連續問題[9-11]．

龔京風等[12-15]發展了一種適用于二維復合材料熱應力研究的格點型有限體積方法(cell vertex FVM, CV-FVM),數值結果表明,CV-FVM能夠有效避免物性參數引起的數值不連續問題．本文進一步將CV-FVM推廣應用于三維問題,通過數值算例驗證計算方法的正確性,并基于CV-FVM分析TBC活塞熱力性能．

1基本方程

考慮穩態情況下各向同性線彈性復合材料的熱應力問題,材料的物性參數隨空間變化．基于控制體Ω建立熱傳導和熱彈性方程,Ω體積為V,邊界面為S．1.1熱傳導方程

熱傳導控制方程為

(1)

式中:ρ、c、T、k分別為密度、比熱容、溫度、熱傳導系數; nα為微元邊界S的單位外法線矢量分量,α=x, y, z; qVT為熱源在單位時間單位體積內產生的熱量,本文不涉及熱源,后文中將省略相應內容．考慮3種邊界條件:

(2)

(3)

(4)

式中:TB為Dirichlet邊界SD上給定的溫度;qB為Neumann邊界SN上給定的法向熱流量;hB為Robin邊界SR上給定的對流換熱系數,T∞為環境溫度．下標B代表邊界．

1.2熱彈性方程

熱彈性控制方程為

式中: uα為位移矢量的分量,σαβ為應力張量的分量,fα為體積力矢量的分量．本文不涉及體積力,后文中將省略相應內容．

利用線彈性體的本構方程及幾何方程,熱彈性方程可寫為

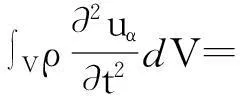
(5)

式中: Γ為熱彈性系數; G、λ為拉姆系數; a為線膨脹系數;Tr為參考溫度,當T=Tr時結構的熱應變為0;δαβ為克羅尼克爾符號,當α=β時δαβ=1,當α ≠ β時δαβ=0．

考慮邊界條件:

(6)

式中: uαB為邊界SD上給定的位移;σnB為邊界SN上給定的法向應力．

2數值離散

對于本文考慮的活塞熱應力問題,數值方法應能夠處理三維非結構化網格．圍繞網格節點依次連接相鄰單元中心和面中心建立控制體,見圖1．空心圓點代表網格節點,實心圓點代表體中心及面中心．用粗實線及虛線圍成網格,細實線及點劃線圍成控制體．關于二維問題的數值離散參考文獻[12-15]．

本文采用交錯網格技術模擬TBC活塞物性參數的空間變化．在網格節點上定義待解變量(溫度和位移),并假設在控制體內均勻分布;將已知量(如物性參數)定義在單元中心,并假設在網格單元內均勻分布．考慮控制體與網格單元的關系,可知控制體內物性參數是變化的,從而在離散過程中考慮空間變化的物性參數．

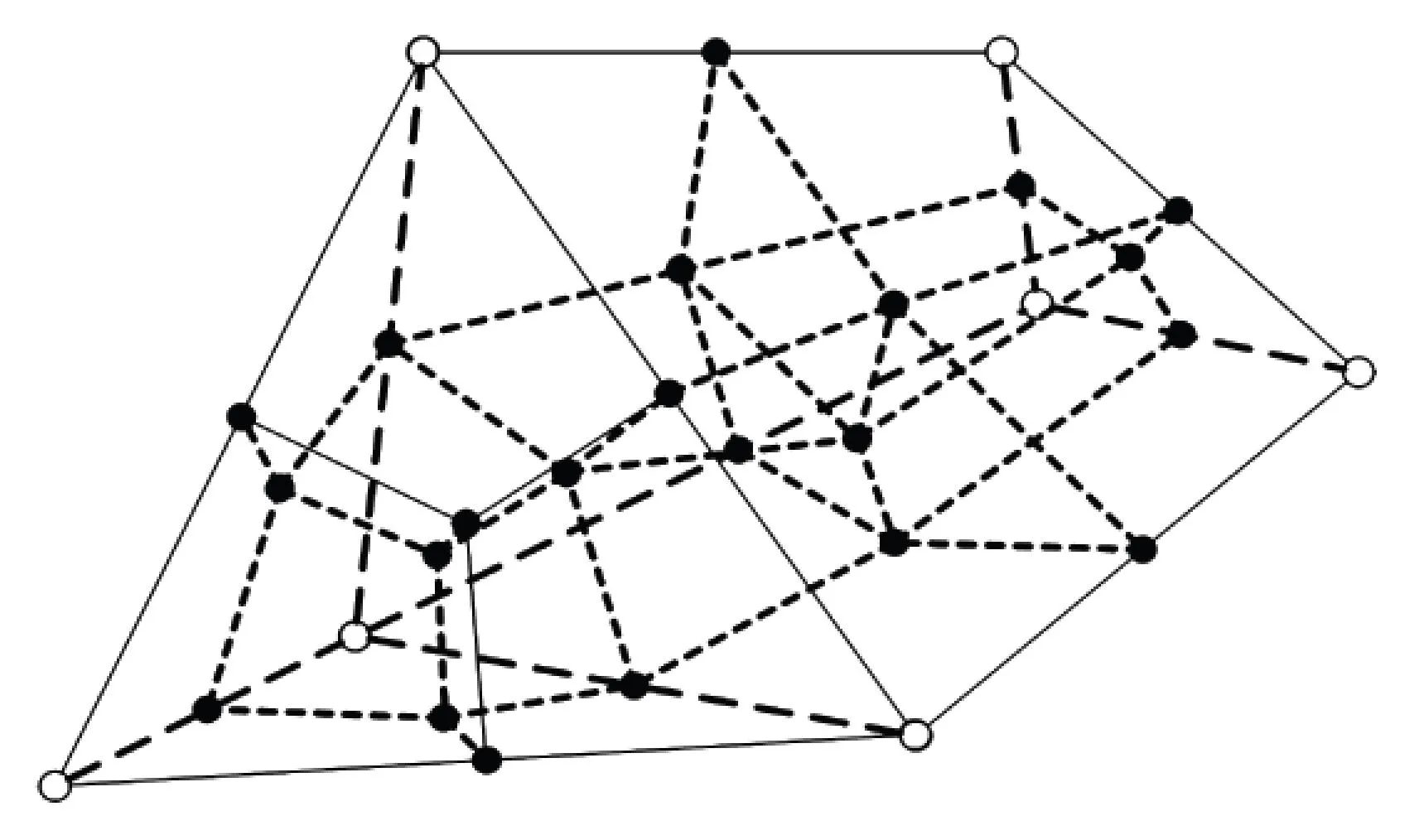
圖1　三維網格示意

2.1熱傳導方程的離散

利用向后差分格式離散熱傳導方程(1)左端的一階時間項,得

式中: t為當前時刻,Δt為時間步長,Vi為當前節點周圍第i個單元的體積,nc為節點周圍單元的總數,ncni為第i個單元的節點數．下標i代表第i個單元中心的變量值．

參考FEM的思想,利用型函數離散方程(1)右端第一項

式中:N為型函數,下標ij代表第i個單元中第j個節點上的變量值．

考慮邊界條件,對于邊界SD上的節點,其溫度直接根據式(2)給定．對于邊界SN和SR上的節點,將式(3)和(4)代入,得到熱傳導方程的最終離散形式:

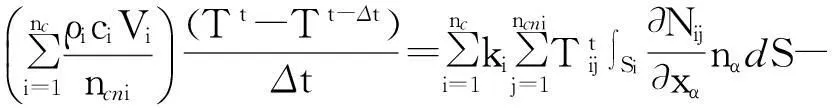
式中:ABi為與節點相鄰的第i個邊界單元面的面積矢量．nN為與當前節點相鄰的位于SN上的面單元數,nR為與當前節點相鄰的位于SR上的面單元數．

2.2熱彈性方程的離散

利用中心差分格式離散熱彈性方程(5)左端的二階時間項,得

參考熱傳導方程空間項的離散方法,離散熱彈性方程(5)右端第一項和第二項

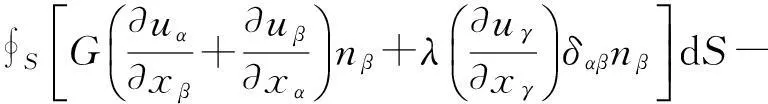
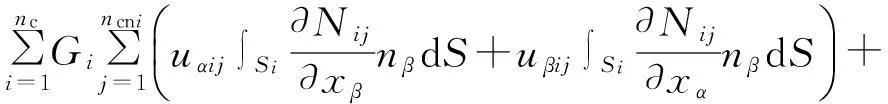
考慮邊界條件,對于SD上的節點,位移給定為uαB．對于SN上的點,將式(6)代入得到熱彈性方程的最終離散形式

2.3數值方法的實施

采用Fortran語言編程實現本文的數值方法．文獻[16-18]采用分離解法求解不同方向的位移方程,即在求解某一方向的位移時,相關的其它位移采用上一次的計算結果,迭代求解各方向位移,直到獲得收斂解．區別于上述文獻,本文采用耦合解法同時求解3個方向位移,從而1次計算即可獲得位移場．不同網格單元的型函數表達式見文獻[18]．

3活塞計算模型

3.1活塞幾何模型及網格模型

模擬活塞熱應力問題,考慮到活塞幾何形狀的對稱性,取如圖2所示的1/4模型,活塞直徑為170mm．活塞模型1與模型2的區別在于,活塞模型1上表面具有避閥坑,沒有布置TBC,通過冷卻油道冷卻活塞頭部;而活塞模型2上表面被簡化了,沒有避閥坑,布置有TBC,沒有冷卻油道,利用TBC的隔熱作用保護活塞頭部．采用四面體單元和棱柱單元劃分計算域,見圖2．

(a) 活塞1網格模型　　　　　 (b) 活塞2網格模型

3.2邊界條件及物性參數

以活塞2為例給出計算邊界條件．活塞x=0及z=0(見圖3)平面為對稱面,設為絕熱邊界,給定簡支位移約束．為了避免活塞的剛體平移,活塞底面給定簡支約束邊界條件．參考文獻[19]中的活塞表面對流換熱系數和環境溫度(由技術參數和經驗公式得到),取平均值做穩態計算．活塞熱邊界條件見圖3和表1．活塞物性參數見表2．

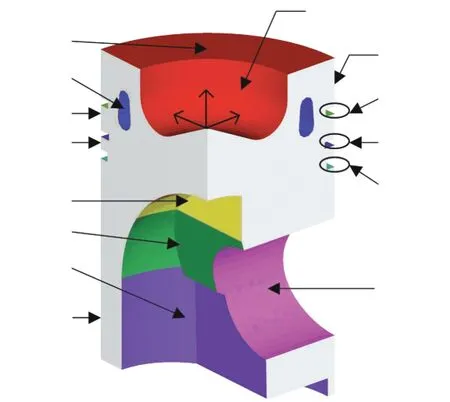
圖3　活塞邊界

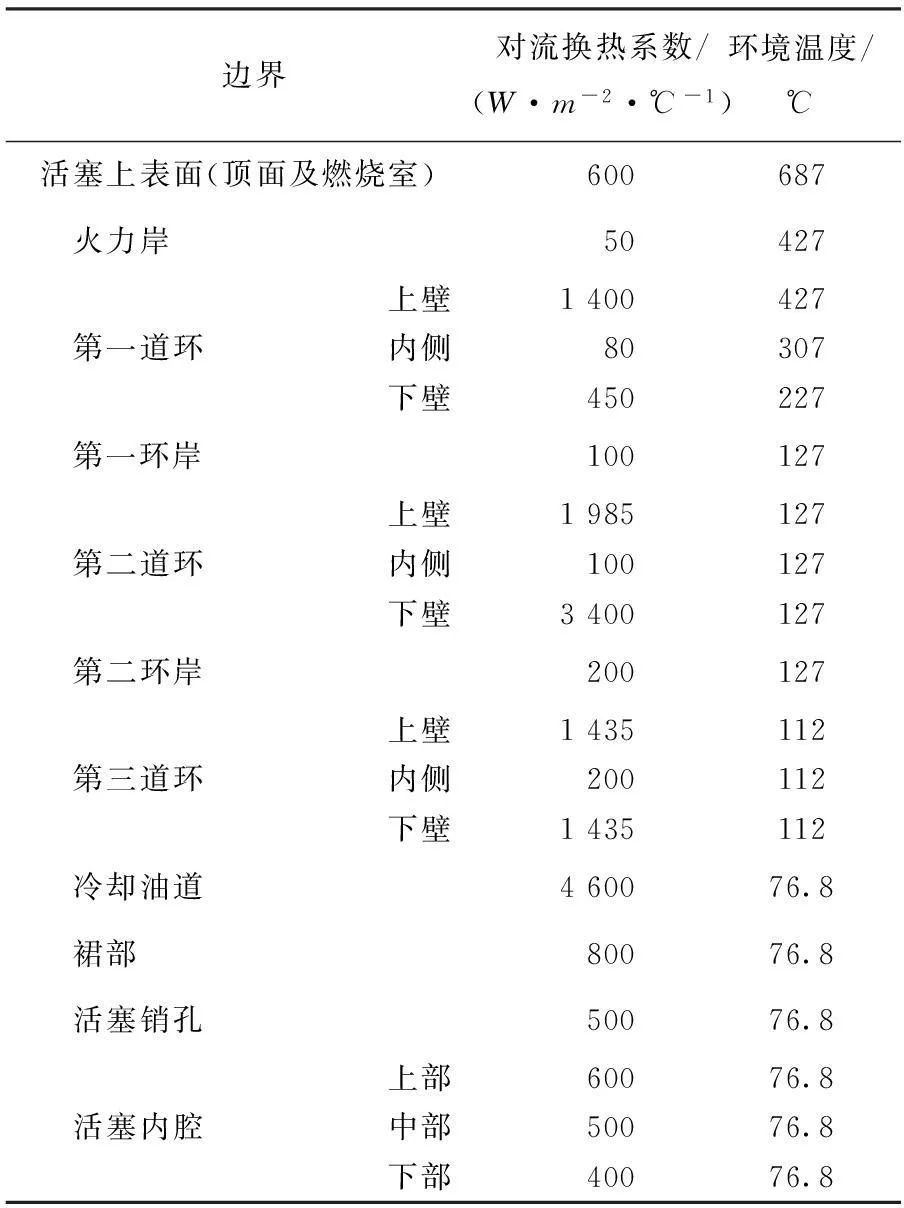
邊界對流換熱系數/(W·m-2·℃-1)環境溫度/℃活塞上表面(頂面及燃燒室)600687 火力岸50427上壁1400427 第一道環內側80307下壁450227 第一環岸100127上壁1985127 第二道環內側100127下壁3400127 第二環岸200127上壁1435112 第三道環內側200112下壁1435112 冷卻油道460076.8 裙部80076.8 活塞銷孔50076.8上部60076.8 活塞內腔中部50076.8下部40076.8

表2　活塞物性參數

4活塞熱應力分析

4.1普通活塞熱應力

為驗證本文數值方法的正確性,數值模擬普通活塞1的熱應力場,活塞材料為硅鋁合金．圖4為不同方法計算得到的45°平面上位移ux云圖．圖5為不同方法計算的45°平面r=0.072m處的應力σxx曲線,其中r=0.072m位于冷卻油腔和活塞環槽之間,熱應力場較為復雜．通過對比可以看出,本文發展的三維CV-FVM計算結果與ANSYS計算結果一致,說明本文三維CV-FVM可用于活塞熱應力數值模擬．

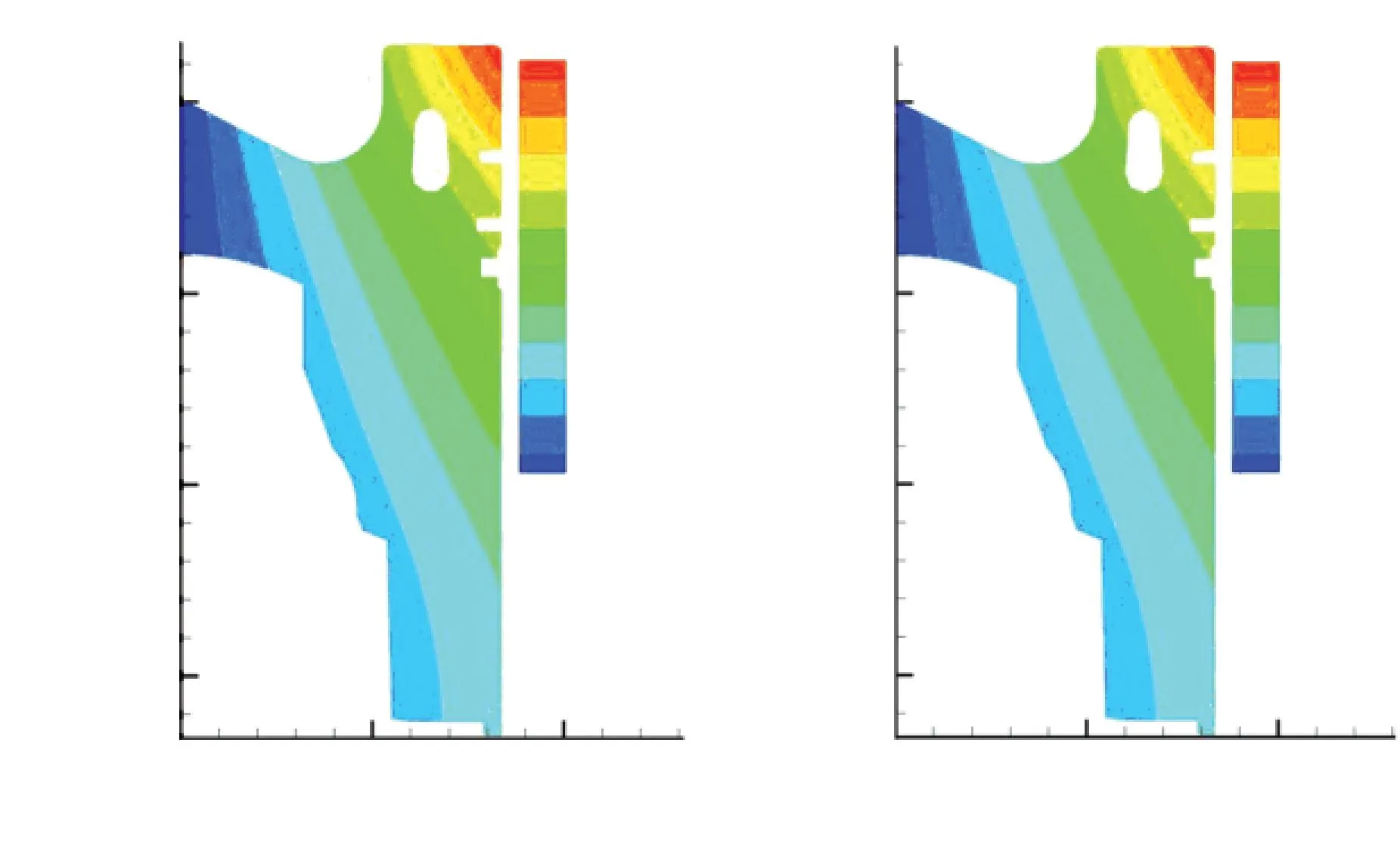
(a) ANSYS計算結果　　　　 (b) CV-FVM計算結果

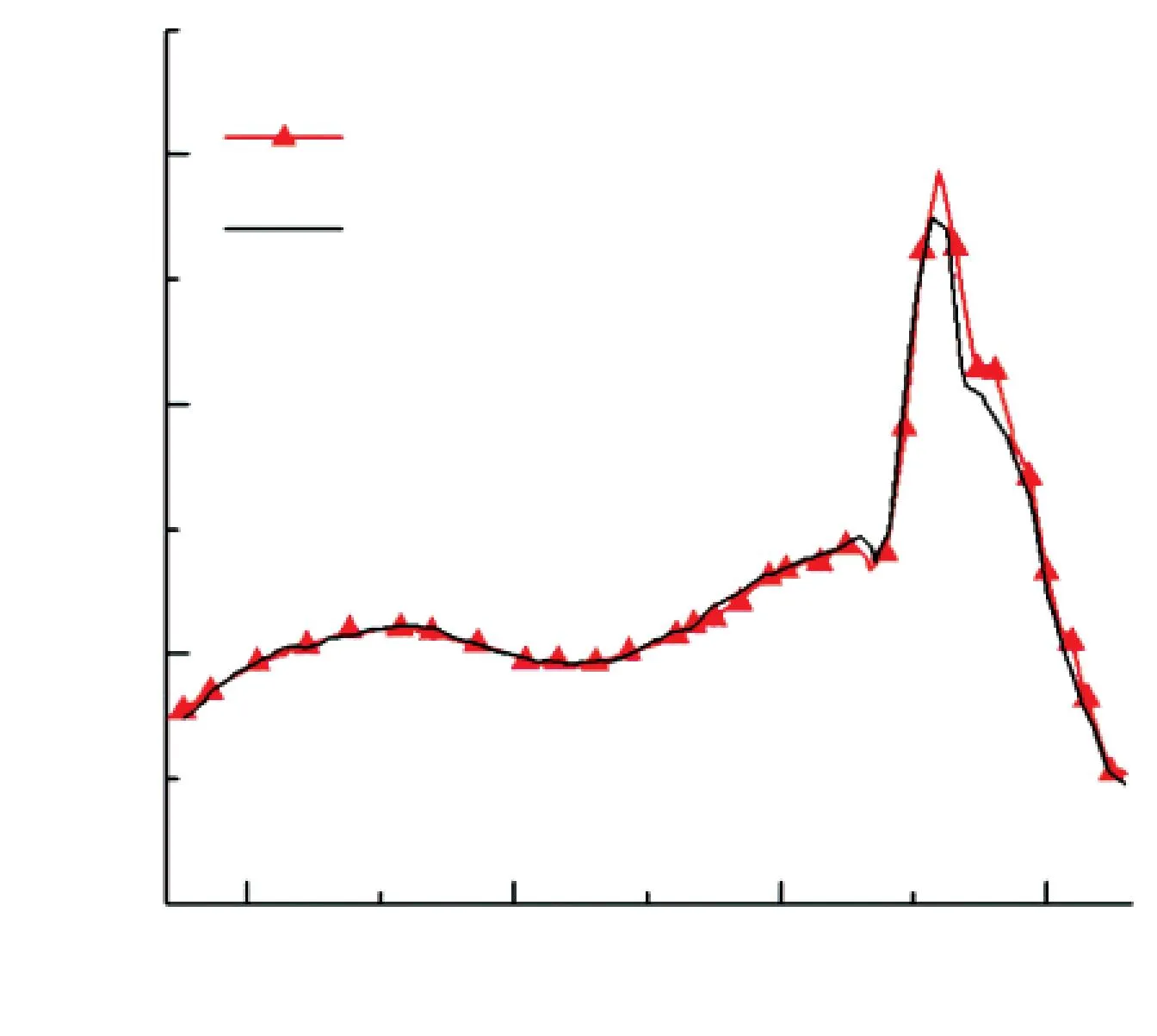
圖5　活塞1的應力σxx曲線對比(45°平面上r=0.072 m處)4.2　TBC活塞熱應力分析

在活塞頂面涂覆1 mm的TBC．活塞基體為鋁硅合金ZL 109,粘結材料為NiCrAl(厚度為0.2 mm),陶瓷材料為MgZrO3(厚度為0.8 mm),材料物性參數見表2．圖6給出了活塞的表面熱流矢量及溫度分布云圖．活塞2表面的TBC承受了大部分的熱載荷,熱流量集中于TBC區域,活塞上表面溫度明顯高于活塞基體溫度．

圖6　活塞2的表面熱流矢量及溫度云圖

圖7為活塞2內θ=45°平面上的熱應力場云圖．由圖可見,活塞的最大溫度T位于燃燒室與活塞頂面的交界區域(A區域),主要原因是A區為活塞上表面轉折位置,相較于其它位置熱阻更大,熱量傳遞更少,因而溫度越高．軸向應力σyy、徑向應力σr和周向應力σθ幅值相當,其最大值位于粘結層與陶瓷層的分界面附近,主要原因是陶瓷層阻隔了大部分的熱量,相對而言傳遞到粘結層、金屬基體的熱量較小,故陶瓷層和粘結層之間的溫度梯度比粘結層和金屬基體間的溫度梯度大得多,陶瓷層和粘結層間存在更大的熱應力．由于TBC內物性參數的突變,TBC區域存在明顯的應力集中現象,容易發生破壞．

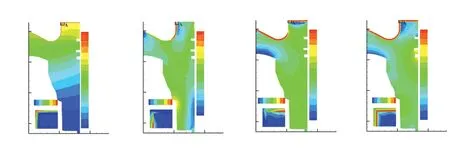
圖7　活塞2的θ=45°平面上熱應力場云圖

分析TBC活塞2上表面θ=45°處的溫度及應力曲線,見圖8．

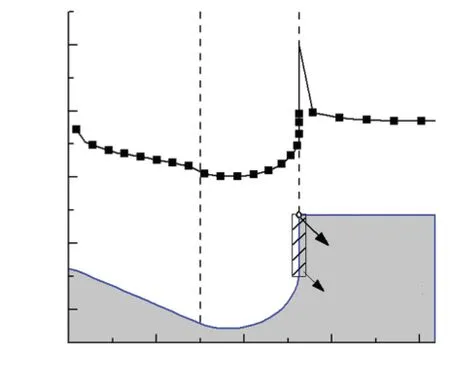
(a) 溫度曲線

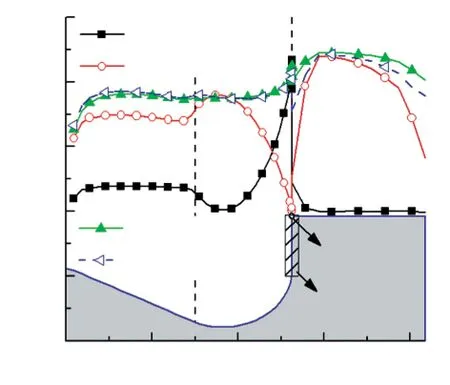
(b) 應力曲線

燃燒室頂面包含3個區域:區域1、區域2位于燃燒室,區域3是活塞頂面．燃燒室邊緣區域用斜線標出．溫度最小值位于區域2,最大值位于B點．參考溫度曲線,可以看到在燃燒室邊緣區域溫度梯度最大,應力在該區域變化幅值相對其他區域大得多．與應力σr和σyy相比,應力σθ沿徑向變化平緩且幅值最大．Von Mises應力σvm可代表活塞的綜合應力情況,其變化趨勢與應力σθ基本一致,說明應力σθ對活塞的整體應力水平起主要影響．

5結論

1) 本文基于CV-FVM求解熱傳導方程和熱彈性方程,將適用于二維復合材料熱應力問題的CV-FVM推廣應用于三維熱應力問題．采用CV-FVM分析普通活塞的熱應力問題,計算結果與商用軟件ANSYS計算結果吻合良好,表明該方法的正確性．

2) 基于CV-FVM進一步分析TBC活塞熱應力場．通過分析活塞熱應力場可知,陶瓷層能夠阻隔活塞頂面的大部分熱量,使得粘結層和陶瓷層間存在較大溫度梯度,引起應力集中,應力最大值出現在粘結層和陶瓷層分界面區域．

3) 通過分析TBC活塞熱應力曲線可知,溫度最大值出現在燃燒室與活塞頂面的交界區域,活塞的應力水平主要受周向應力σθ影響．

4) TBC活塞熱應力場沒有出現數值不連續現象,CV-FVM能夠作為TBC活塞熱力性能研究的數值預測工具．

參考文獻

[1] 王素, 倪春陽, 朱心雄. 功能梯度材料活塞三維溫度場分析[J]. 北京航空航天大學學報, 2005, 31(12): 1299-1302.

[2] 王素, 倪春陽, 朱心雄. 一種功能梯度材料活塞的材料梯度方程選擇[J]. 機械科學與技術, 2006, 25(2): 133-138.

[3] 王素, 倪春陽, 朱玉明, 等. 陶瓷纖維梯度增強活塞的梯度方程研究[J]. 航空學報, 2007, 28(1): 234-239.

[4] BUYUKKAYA E, CERIT M. Thermal analysis of a ceramic coating diesel engine piston using 3-D finite element method[J]. Surface and Coatings Technology, 2007, 202(2): 398-402.

[5] BUYUKKAYA E. Thermal analysis of functionally graded coating AlSi alloy and steel pistons[J]. Surface and Coatings Technology, 2008, 202(16): 3856-3865.

[6] CERIT M. Thermo mechanical analysis of a partially ceramic coated piston used in an SI engine[J]. Surface and Coatings Technology, 2011, 205(11): 3499-3505.

[7] CERIT M, AYHAN V, PARLAK A, et al. Thermal analysis of a partially ceramic coated piston: Effect on cold start HC emission in a spark ignition engine[J]. Applied Thermal Engineering, 2011, 31(2/3): 336-341.

[8] ABOUDI J, PINDERA M J, ARNOLD S M. Higher-order theory for functionally graded materials[J]. Composites, Part B, 1999, 33: 777-832.

[9] SANTARE M H, LAMBROS J. Use of graded finite elements to model the behavior of nonhomogeneous materials[J]. ASME Journal of Applied Mechanics, 2000, 67(4): 819-822.

[10]KIM J H, PAULINO G H. Isoparametric graded finite elements for nonhomogeneous isotropic and orthotropic materials[J]. ASME Journal of Applied Mechanics, 2002, 69(4): 502-514.

[11]CAVALCANTE M A A, MARQUES S P C, PINDERA M J. Parametric formulation of the finite-volume theory for functionally graded materials-Part II: numerical results [J]. Journal of Applied Mechanics, 2007, 74(5): 946-957.[12]GONG J F, XUAN L K, MING P J, et al. Thermoelastic analysis of functionally graded solids using a staggered finite volume method[J]. Composite Structures, 2013, 104: 134-143.

[13]GONG J F, XUAN L K, MING P J, et al. An unstructured finite-volume method for transient heat conduction analysis of multilayer functionally graded materials with mixed grids[J]. Numerical Heat Transfer: Part B, 2013, 63(3): 222-247.

[14]GONG J F, XUAN L K, MING P J, et al. Application of the staggered cell-vertex finite volume method to thermoelastic analysis in heterogeneous materials[J]. Journal of Thermal Stresses, 2014, 37(4): 506-531.

[15]龔京風, 明平劍, 宣領寬, 等. 基于有限體積法求解FGM動態響應及固有特性[J]. 華中科技大學學報(自然科學版), 2013, 41(5): 28-33.

[16]TAYLOR G A, BAILEY C, CROSS M. Solution of the elastic/visco-plastic constitutive equations: a finite volume approach[J]. Applied Mathematical Modelling, 1995, 19(12): 746-760.

[17]BAILEY C, CROSS M. A finite volume procedure to solve elastic solid mechanics problems in three dimensions on an unstructured mesh [J]. International Journal for Numerical Methods in Engineering, 1995, 38(10): 1757-1776.

[18]TAYLOR G A, BAILEY C, CROSS M. A vertex-based finite volume method applied to non-linear material problems in computational solid mechanics[J]. International Journal for Numerical Methods in Engineering, 2003, 56(4): 507-529.

[19]劉友. 船用柴油機活塞瞬態溫度場測試與分析研究[D]. 哈爾濱: 哈爾濱工程大學, 2013.

(編輯楊波)

Cell vertex FVM for thermoelastic analysis of the piston with thermal barrier coating

GONG Jingfeng1, XUAN Lingkuan1, ZHOU Shaowei1, MING Pingjian2

(1. China Ship Development and Design Center, Wuhan 430064, China;2. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract:To analyze the performance of the piston with thermal barrier coating (TBC), two dimensional cell vertex FVM (CV-FVM) has been extended to the research of the thermoelastic performance of three-dimensional composite structures. The staggered grid technique was adopted to incorporate property variation into the course of solution so as to avoid numerical discontinuity. The unknown variable was defined at the cell vertex, while the material property was defined at the cell center. The developed CV-FVM was used to simulate the thermoelastic fields of the ordinary piston and the predicted results agreed with the ANSYS results. Then, the CV-FVM was used to simulate the thermoelastic fields of the TBC piston and the performance were analyzed. The maximum temperature is in the area between the combustion chamber and the top surface, and the maximum stress is around the interface between the ceramic layer and the cohesive layer. The circumferential stress contributes the main part of the thermoelastic stress in the TBC area. The successful application demonstrates that the CV-FVM can be used as a predictive tool for the thermoelastic analysis of the TBC piston.

Keywords:staggered grid technique; cell vertex FVM; thermal barrier coating; piston; thermoelastic

doi：10.11918/j.issn.0367-6234.2016.07.012

收稿日期:2015-05-03

基金項目:國家自然科學基金(51206031)

作者簡介:龔京風(1986—),女,博士,工程師

通信作者:宣領寬, xuanlingkuan@163.com

中圖分類號:TK422

文獻標志碼:A

文章編號:0367-6234(2016)07-0076-06