Kepler問題的離散化和積分理論

劉長欣, 裴利軍, 夏麗莉

(1. 河南教育學院 物理與電子工程學院 河南 鄭州 450046;2. 鄭州大學 數學與統計學院 河南 鄭州 450001)

Kepler問題的離散化和積分理論

劉長欣1, 裴利軍2, 夏麗莉1

(1. 河南教育學院 物理與電子工程學院 河南 鄭州 450046;2. 鄭州大學 數學與統計學院 河南 鄭州 450001)

引入差分離散變分原理, 得到了Hamilton形式下的Kepler系統的差分方程、能量演化方程和系統的保辛數值算法格式，給出了離散Kepler系統的Noether定理. 數值計算Kepler系統的運動軌跡、時間歷程和守恒量, 并和傳統的4階R-K方法比較, 說明離散變分算法能夠較好地保持系統的穩定性和具有較高的計算精度.

差分離散變分原理; 離散Kepler系統; Noether對稱性; 守恒量

0 引言

文獻[1]提出了離散變分原理. 文獻[2-3]發展了這一理論并應用力學系統得到系統的第一積分. 在數學領域，有關差分方程的研究也很普遍[4-5].為了提高差分自回歸移動平均模型的擬合精度,文獻[6]討論了改進的差分自回歸移動平均模型的共軛梯度參數估計法.文獻[7]討論了一類特殊離散系統的周期解的存在性.對離散力學已經得到了離散形式的Euler-Lagrange 方程和離散版本的Noether定理, 但是在時間-空間坐標中, 只能得到動量守恒. 為了探討系統的能量守恒, 著名物理學家李政道教授給出了離散變分原理[8], 得到離散動量守恒和離散能量守恒. 因此, 在研究Lagrange 形式的離散力學時可以自然地引入離散的Legenda變換, 處理Hamilton形式的離散力學[9-10].

Kepler問題有三個著名的守恒量:能量守恒、角動量守恒和Runge-Lenz矢量守恒[11]. 文獻[12]研究了Kepler問題的辛算法，得到了能穩定描述Kepler方程解的時間歷程, 文獻[13-14]基于辛方法給出了系統Hamilton能量守恒和角動量守恒. 文獻 [15-16] 分別基于Levi-Civita 和 Kustaanheimo-Stiefel 變換，研究了二維和三維Kepler系統的保能量守恒的數值算法. 文獻 [17-18] 推廣了Levi-Civita 和 Kustaanheimo-Stiefel 變換，給出了更廣泛的L-變換，得到了能量守恒、角動量守恒和Runge-Lenz矢量守恒. 在尋求Kepler問題的守恒量過程中, 對稱性理論的優勢得到了體現，其為尋求Kepler問題的守恒量提供了一條簡潔重要的途徑. 文獻 [19] 研究微擾Kepler系統軌道方程的近似Lie對稱性, 得到6個一階近似不變量. 文獻 [20] 研究了Kepler方程 Noether-Lie對稱性與守恒量. 雖然Kepler系統的連續對稱性問題得到了一定的發展，但是對于Kepler系統的離散對稱性和守恒量的研究較少.本文通過研究 Kepler 系統的離散化、數值算法和積分理論，得到一種更加簡潔的探究Keple系統的守恒量的路徑.

1 離散Kepler系統的運動方程

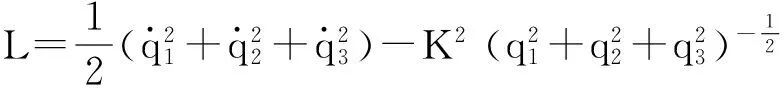
(1)

基于顯含差分項的方法, Kepler系統的離散Lagrange函數為

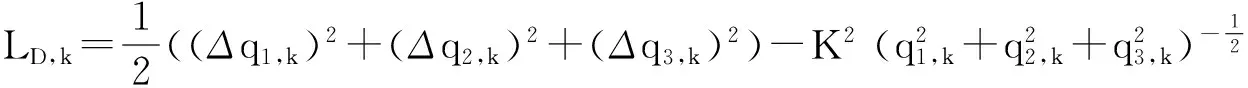
(2)

引入離散Legenda變換：

(3)

這里HD,k=HD,k(tk,qi,k,pi,k+1). 則離散Kepler系統的Hamilton函數可表示為

(4)

離散形式的Hamilton泛函表示為

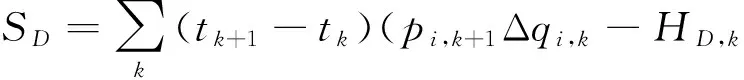
(5)

離散形式Hamilton作用量式(5)的全變分為

考慮到 Δ(δtqi,k)=δtΔqi,k+(Δδttk)·Δqi,k和離散 Leibniz 法則， Δ(fkgk)=(Δfk)gk+fk+1(Δgk), 離散Hamilton 作用量的全變分可展開為

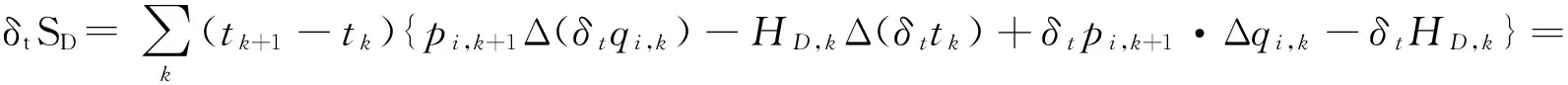
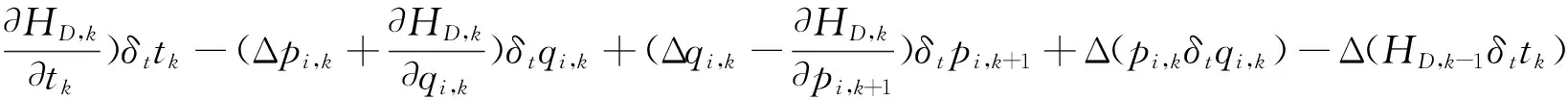
(6)

取離散時間tk、廣義坐標qi,k和廣義動量pi,k的無限小變換群：

(7)

由離散全變分原理δtSD=0, 對應于離散序列的變分δttk的系數為零, 可得

(8)

(8)式為離散差分序列Hamilton系統的能量演化方程，分別對應于離散序列的變分δtqi,k和δtpi,k+1的系數為零, 可得：

(9)

(9)式正是離散差分序列Kepler系統的Hamilton正則方程, 也稱為離散Kepler系統的變分積分子. 式(8)、式(9)稱為離散差分序列Hamilton系統的差分動力學方程，式(9)也稱之Kepler系統的變分積分子[21]，為基于差分變分原理的保辛數值算法格式.

2 離散Kepler系統的Noether定理

定義1 如果Hamilton作用量式(5)是Kepler系統在無限小變換式(7)下的不變量, 即對每一個無限小變換,δtSD=0始終成立, 則稱此無限小變換是Noether意義下的對稱變換.

判據1 對于無限小變換式(7), 如果滿足

(10)

則變換(7)是Kepler系統的對稱變換.

定理1 如果給定的無限小變換式(7)是Kepler系統的對稱變換, 即滿足等式

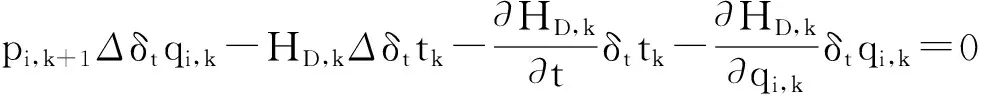
(11)

則Kepler系統式(8)、(9)存在守恒量

IN,S=pi,kδtqi,k-HD,k-1δttk=const.

(12)

證明 Hamilton作用量的離散全變分可表示為

考慮到式(6), 有

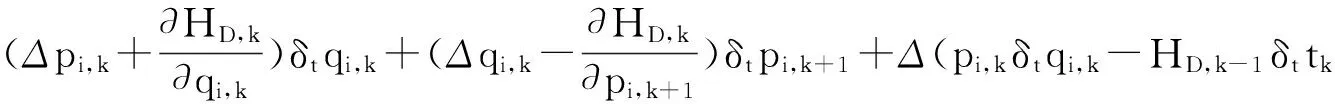
(13)

將Kepler系統的差分方程(8)、(9)式代入式(13), 考慮到式(11), 得守恒量(12)式.

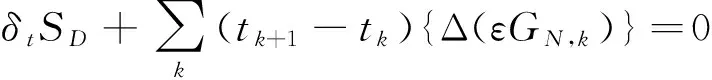
(14)

則變換式(7)是Kepler系統的準對稱變換.

定理2 如果給定的無限小變換(7)是Kepler系統的準對稱變換, 即滿足等式

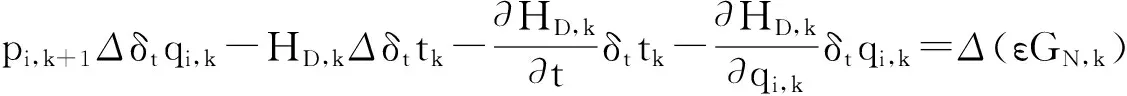
(15)

則Kepler系統式(8)、(9)存在守恒量

IN,S=pi,kδtqi,k-HD,k-1δttk+εGN,k=const.

(16)

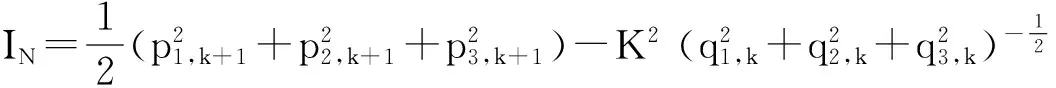
(17)

定理2說明取不同的對稱性生成元和合適的規范函數, 可能得到更多的守恒量. 本文只給出了能量守恒.

圖1 R-K方法和離散變分方法求解Kepler系統的時間歷程Fig.1 Displacements of phase space with variational methods and the Runge-Kutta methods

3 數值計算

基于離散差分變分原理, 數值研究Kepler系統方程(2)的運動問題. 選擇初始條件為q1=0.003，q2=0.9,q3=0.01,p1=0.1,p2=0.1和p3=0.8的Kepler軌道并取步長為0.1, 常數K=0.75. 根據Kepler系統的變分積分子式(9), 圖1給出了系統運動軌道曲線, 并和傳統的4階Runge-Kutta方法進行比較. 從圖1中可以看出, 采用離散變分算法較好地刻畫了系統的軌跡.

圖2給出了系統的解曲線. 從圖2中可以看出, 本文方法比傳統的4階Runge-Kutta方法的結果更加精確.

圖2 R-K方法(左)和離散變分方法(右)求解Kepler系統的運動軌跡

圖3給出了系統的能量誤差隨時間的變化規律, 基于差分變分原理的離散化方法能夠保持系統的總能量守恒, 符合問題的實際情況. 當時間逐步增加時, 總能量也能很好地保持守恒. 采用Runge-Kutta方法所得的總能量隨時間逐漸耗散.

圖4給出了離散Noether守恒量隨時間的變化趨勢, 從圖4可以看出基于差分變分原理的Noether定理所得的守恒量是守恒的. 這些結果體現了離散變分計算方法相比于Runge-Kutta方法具有較高的精度和較好的穩定性.

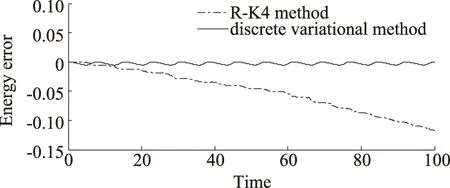
圖3 R-K方法和離散變分方法求解Kepler系統的能量誤差

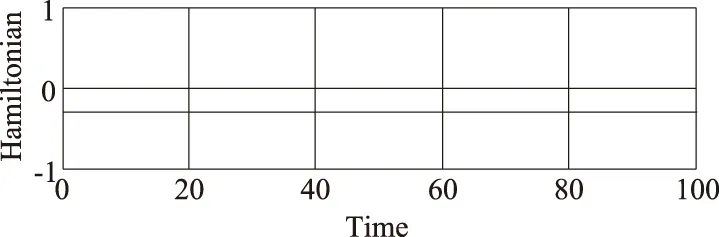
圖4 離散變分方法求解Noether守恒量(17)

4 結論

將差分視作一個幾何對象, 引入離散差分變分原理研究離散Kepler系統的對稱性和守恒量理論, 得到了離散的Noether定理, 從Noether定理得到的Noether守恒量恰好是系統的能量. 這些結果與連續系統的結果具有較好的一一對應關系. 數值計算結果也驗證了基于離散差分變分原理的離散化方法具有較好的保系統的結構和守恒量的優勢.

[1] CADZOW J A. Discrete calculus of variations[J]. Int Control, 1970, 11 (3): 393-407.

[2] MAEDA S. Canonical structure and symmetries for discrete systems[J]. Math japonica, 1980, 25(4): 405-420.

[3] LOGAN J D. First integrals in the discrete variational calculus[J]. Aequationes math, 1973, 9 (2-3): 210-220.

[4] 趙良鵬, 閆衛平. 帶有強迫項的高階差分方程解的振動性[J]. 鄭州大學學報(理學版), 2014, 46 (3): 5-8.

[5] 江山, 易年余, 孫美玲. 拋物型微分方程的多尺度有限元高效計算[J]. 揚州大學學報(自然科學版) 2015,18 (2):26-30.

[6] 單銳, 劉雅寧, 劉文. 改進的差分自回歸移動平均模型的共軛梯度參數估計法[J]. 河南科技大學學報(自然科學版), 2015, 36 (4): 85-90.

[7] 薛艷昉, 廖家鋒. 離散p-Laplace系統周期解的存在性[J]. 信陽師范學院學報(自然科學版), 2015, 28(118):29-32.

[8] LEE T. Can time be a discrete dynamical variable [J]. Physics letters B, 1983，122(3): 217-220.

[9] GUO H Y, LI Y Q, WU K. difference discrete variational principles, Euler-Lagrange cohomology and symplectic, multisymplectic structures I: difference discrete variational principle[J]. Commun Theor Phys, 2002, 37 (1): 1-10.

[10]吳可, 郭漢英. 變分和上同調的差分離散形式及其應用[J]. 首都師范大學學報 (自然科學版), 2006, 27 (5): 1-14.

[11]THIRRING W. A Course in Mathematical Physics, vol.I: Classical Dynamical Systems[M]. New York: springer, 1978.

[12]SANZ-SERNA J M, CALVO M P. Numerical Hamiltonian problems[M]. London: Chapman & Hall, 1994.

[13]PRINCE G E, ELIEZER C J. On the Lie symmetries of the classical Kepler problem[J].Joumal of physics a general physics, 1981, 14: 587-596.

[14]LEACH, P G L. Applications of the Lie theory of extended groups in Hamiltonian mechanics: the oscillator and the Kepler problem[J]. J Austral Math Soc, 1981, 23(2) : 173-186.

[15]MINASAKI Y, NAKAMURA Y. A new discretization of the Kepler motion which conserves the Runge-Lenz vector[J]. Phys Lett A, 2002, 306 (2/3): 127-133.

[16]MINESAKI Y, NAKAMURA Y. A new conservative numerical integration algorithm for the three-dimensional Kepler motion based on the Kustaanheimo-Stiefel regularization theory[J]. Phys Lett A, 2004, 324 (4) : 282-292

[17]KOZLOV R. A conservative discretization of the Kepler problem based on theL-transformations[J]. Phys Lett A 2007, 369 (2): 262-273.

[18]KOZLOV R, Conservative discretizations of the Kepler motion[J]. J Phys A Math Theor , 2007, 40(40): 4529-4539.

[19]樓智美. 微擾Kepler系統軌道微分方程的近似Lie對稱性與近似不變量[J]. 物理學報, 2010 , 59(10) : 6764-6769.

[20]殷保祥, 劉曉巍, 李元成, 等. Kepler方程的Noether-Lie對稱性與守恒量[J]. 江西科學，2012,30(5)：569-571.

[21]XIA L L，CHEN L Q. Mei symmetries and conserved quantities for non-conservative Hamiltonian difference systems with irregular lattices[J]. Nonlinear dynamics, 2012, 70(2):1223-1230

(責任編輯：方惠敏)

Discretization and Integration Theory of the Kepler System

LIU Changxin1, PEI Lijun2, XIA Lili1

(1.CollegeofPhysicsandElectronicEngineering,HenanInstituteofEducation,Zhengzhou450046,China;2.SchoolofMathematicsandStatistics,ZhengzhouUniversity,Zhengzhou450001,China)

The canonical Hamiltonian difference equations and the energy equation of the Kepler system were proposed by introducing the discrete difference variational principle. The symplectic numerical algorithm was proposed for this equation. The discrete Noether theorem of the Kepler system was presented by means of difference discrete variational principle with the difference being regarded as an entire geometric object. The numerical calculations of the trajectory, the sollution and the three types of conserved quantities were shown. The difference discrete variational method preserved the exactness and the invariant quantity.

discrete difference variational principle； discrete Kepler system； Noether symmetries； the conserved quantities

2015-11-18

國家自然科學基金資助項目(11502071)；河南省自然科學基金資助項目(132300410051)；河南省教育廳基礎研究項目(13A140224).

劉長欣(1966—)，男，河南南陽人，副教授，主要從事動力學系統方程的可積性研究，E-mail: Lcx19662008@163.com; 通訊作者：裴利軍(1974—)，男，河南武陟人，教授，主要從事時滯微分方程、物理和力學中的數學方法和數值計算研究， E-mail: peilijun@zzu.edu.cn; peilijun99@163.com.

劉長欣,裴利軍,夏麗莉.Kepler問題的離散化和積分理論[J].鄭州大學學報(理學版)，2016,48(2)：29-33.

O316

A

1671-6841(2016)02-0029-05

10.13705/j.issn.1671-6841.2015274