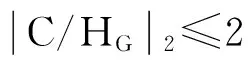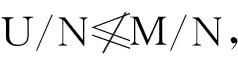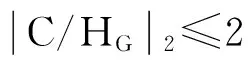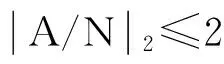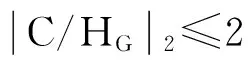關于有限群子群的θ-完備
高 輝, 高勝哲, 尹 麗
(大連海洋大學 理學院 遼寧 大連 116023)
關于有限群子群的θ-完備
高 輝, 高勝哲, 尹 麗
(大連海洋大學 理學院 遼寧 大連 116023)
利用新的思路將子群的θ-完備的條件互相結合, 或者與c-正規的條件結合起來,研究有限群的可解性.
子群;θ-完備;c-正規; 可解群
0 引言
利用有限群子群,特別是利用一些特定子群的性質來刻畫有限群的結構尤為突出. 有限群極大子群的完備或θ-子群偶的概念的提出, 為研究有限群的性質提供了一個很好的工具. 另外, 以HG表示H在G中的核, 記CG為子群C在G中的正規閉包. 為了揭示極大子群的完備和θ-子群偶之間的關系, 文獻[1]給出了極大子群的θ-完備的定義.
定義1 給定有限群G的極大子群M, 稱G的子群C為關于M的θ-完備, 如果C滿足:
(1)CM;(2)MG?C;(3)C/MG不真含G/MG的異于1的正規子群.
進一步地, 若不存在關于M的滿足C 從有限群的極大子群的θ-完備的定義可以看出, 其只適用于有限群的極大子群. 而有限群除了極大子群外, 還有許多其他子群對有限群的結構也有重要的影響, 也是人們研究的重點. 為此將極大子群的θ-完備應用到一般子群上, 文獻[8]引入了一般子群的θ-完備概念. 定義2 設H是G的一個真子群,G的一個子群C稱為H在G中的一個θ-完備, 如果C滿足: (1)G= 用θI(H)表示H在G中的所有的θ-完備組成的集合,θI(H)按集合包含關系做成一個偏序集, 其極大元稱為H的一個極大θ-完備. 即不存在關于H的滿足C 另一方面, 正規子群是群論中的一個重要概念,隨著群論的發展,一些比正規性弱的子群的概念也被相繼提出,例如,s-擬正規,半正規,c-正規等.文獻[9]提出了c-正規的概念. 定義3 令H≤G,H叫做c-正規的, 如果存在KG,使得G=HK,且H∩K?HG. 探討一般子群的θ-完備對群結構的影響,主要是將2-極大子群的θ-完備的條件或者與c-正規條件結合起來討論群的可解性, 得到了有限群可解的一些充分條件. 定義4[10]如果有M<·G使H<·M,稱群G的子群H為G的一個2-極大子群. 引理1[8]設H是G的真子群,N≤H且NG,C是H的一個極大θ-完備當且僅當C/N是H/N的極大θ-完備. 鄂州物業管理可以結合地方實際情況從以下幾個方面進行規范:第一嚴把市場準入關。對物業管理企業要嚴格準入,強化新建企業開業登記和資格審查、年檢、資質復審等工作;第二建立物業管理主體信用檔案。對物業公司及其法人、業委會成員建立誠信檔案;第三積極開展物業管理考評。根據優秀物業管理示范小區標準,積極開展考評達標活動,讓更多的業主購得安心和住得放心;最后加強制度建設。應根據國家和省公布的法律法規來制定與地方配套的、具體的細則及辦法,進而推動鄂州市物業管理規范化發展。 引理4[8]設G非可解, 且G的每個真子群H都存在一個極大θ-完備C. 若N是G的唯一極小正規子群且N非可解, 而C是有Sylow塔, 則C是G的極大子群. 引理 5[11]設G=AB, 子群A,B的Sylow 2-子群的階不超過2, 那么G是可解的. 引理6[10]設H為G的極大子群, 若H冪零,且H的Sylow 2-子群的冪零類≤2, 則G可解. 定理1 令G是一個群, 假設對于G的2-極大子群H, 存在一個關于H的極大θ-完備C, 滿足下列條件之一: 則G可解. 推論2 令G是一個群, 假設對于G的2-極大子群H, 存在一個關于H的極大θ-完備C, 使得CG/HG可解, 則G可解. 定理2 對于G的每個2-極大子群H, 存在一個關于H的極大θ-完備C或者C/HG冪零, 且Sylow2-子群的冪零類不超過2, 或者H在G中c-正規, 則G可解. 推論3 對于G的每個2-極大子群H, 存在一個關于H的極大θ-完備C使得C/HG冪零, 且Sylow 2-子群的冪零類不超過2, 則G可解. 推論4 對于G的每個2-極大子群H, 若H在G中c-正規, 則G可解. 定理3 假設G是有限群,N是G的非平凡的正規子群, 如果對于G的每個不包含N的2-極大子群H, 存在一個關于H的極大θ-完備C使得C/HG冪零, 且Sylow 2-子群的冪零類不超過2, 則G可解. 證明 假設定理不成立, 令G為極小階反例. 假設R是G的極小正規子群,H/R是G/R的2-極大子群, 且NR/R≤H/R, 則H是G的2-極大子群且N≤H, 由題設知,存在一個關于H的極大θ-完備C使得C/HG冪零, 且Sylow 2-子群的冪零類不超過2. 由 引理1知,G/R滿足定理的條件. 由極小階反例知,G/R可解, 從而NR/R可解.若N∩R=1, 則N?NR/R可解. 若N∩R=R, 則R≤N, 且N/R可解. 進一步假設R是G的唯一的極小正規子群且RΦ(G),R非可解. 因為RΦ(G), 則存在G的極大子群L使得RL,NL且LG=1.假設T<·L<·G, 則NT且TG=1. 由題設知, 存在一個關于T的極大θ-完備D使得D冪零,且Sylow2-子群的冪零類不超過2. 顯然,D. 由引理3知,D<·DR. 由引理6知,DR是可解的, 從而R可解, 與R非可解矛盾. 定理4 如果G有一個可解的2-極大子群H,H有一個極大θ-完備C, 使得CG/HG可解, 則G可解. 證明 (1) 若HG≠1, 則G非單. 假設N是G的極小正規子群, 并且N≤H, 由題設可知,H有一個極大θ-完備C, 使得CG/HG可解. 由引理1可知,C/N是H/N的極大θ-完備,并且(C/N)G/N/(H/N)G/N?CG/N/HG/N?CG/HG可解. 由歸納法知,G/N可解.又N可解, 所以G可解. (2) 若HG=1, 由題設知,H有一個極大θ-完備C,使得CG可解. 由定義2知,G≤H,C≥CGH. 于是G/CG?H/(H∩CG)可解, 又CG可解, 所以G可解. [1] ZHAO Y Q. On the Deskins completions, theta completions and theta pairs for maximalsubgroups I[J]. Comm Algebra, 1998, 26(10): 3141-3153. [2] ZHAO Y Q. On the Deskins completions, theta completions and theta pairs for maximalsubgroups II[J]. Comm Algebra, 1998, 26(10): 3155-3164. [3] LI S R, ZHAO Y Q. Ons-completions of maximal subgroups of finite groups [J]. Algebra Colloq, 2004, 11(3): 411-420. [4] 杜妮, 李世榮. 關于有限群極大子群的強θ-完備[J]. 數學年刊, 2006, 27A(2): 279-286. [5] LI S R. OnF-abnormal maximal subgroups of finite groups[J]. Acta Math, 2007, 23(5): 885-888. [6] 石向東, 韋華全, 馬儇龍. 乘積因子群的共軛類長與有限群結構[J]. 鄭州大學學報(理學版), 2013, 45(2): 10-13. [7] 陳松良,蔣啟燕. 關于108階群的完全分類[J].鄭州大學學報(理學版), 2013, 45(1): 10-14. [8] 高輝, 高勝哲, 尹麗. 子群的θ-完備和群的結構[J]. 山東大學學報(理學版), 2014, 49(3): 43-45. [9] WANG Y M.c-normality of groups and its properties[J]. J Algebra, 1996, 78(180): 754-765. [10]徐明耀. 有限群導引(上、下冊)[M]. 北京:科學出版社, 1999. [11]鐘祥貴. 關于有限群極大子群的極大完備[J]. 廣西科學, 2002, 9(3): 161-163. (責任編輯:方惠敏) Onθ-Completions for Subgroups GAO Hui, GAO Shengzhe, YIN Li (ScienceInstitute,DalianOceanUniversity,Dalian, 116023,China) The solvability of the finite group was studied by using new methds to combine the conditions ofθ-completions for subgroups with each other, or with that ofc-normal. subgroups ;θ-completions;c-normal ; solvable groups 2015-11-08 高輝(1978—),女,遼寧莊河人,講師,碩士,主要從事有限群研究,E-mail:gaohui@dlou.edu.cn;通訊作者:高勝哲(1974—),男,黑龍江大興安嶺人,副教授,碩士,主要從事有限群及金融數學研究,E-mail:gsz@dlou.edu.cn. 高輝,高勝哲,尹麗.關于有限群子群的θ-完備[J].鄭州大學學報(理學版),2016,48(2):11-13. O152.1 A 1671-6841(2016)02-0011-03 10.13705/j.issn.1671-6841.20152341 引理

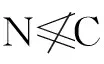
2 主要結果