Mikhauilov-Novikov-Wang方程族及其bi-Hamilton結構與守恒律

何國亮， 張永三

(1.鄭州輕工業學院 數學與信息科學學院 河南 鄭州 450002；2.河南機電職業學院 人文與藝術設計系 河南 鄭州 451191)

Mikhauilov-Novikov-Wang方程族及其bi-Hamilton結構與守恒律

何國亮1， 張永三2

(1.鄭州輕工業學院 數學與信息科學學院 河南 鄭州 450002；2.河南機電職業學院 人文與藝術設計系 河南 鄭州 451191)

借助于零曲率方程得到了與3×3矩陣譜問題相聯系的Mikhauilov-Novikov-Wang方程族. 利用跡恒等式和兩個斜對稱算子, 建立了該族方程的bi-Hamilton結構. 從兩個線性譜問題出發給出了Mikhauilov-Novikov-Wang方程的無窮多守恒律.

Mikhauilov-Novikov-Wang方程族； bi-Hamilton結構； 守恒律

0 引言

五階偏微分方程[1-3]

ut=-uxxxxx+10uuxxx+25uxuxx-20u2ux

(1)

在物理和數學學科中發揮著重要作用. 方程(1)可以從如下的 Mikhauilov-Novikov-Wang (MNW) 方程得到(令v=0)[4]

ut=-uxxxxx+10uuxxx+25uxuxx-20u2ux+9vx,vt=3vuxxx-4u2vx+vxuxx-24uvux.

(2)

因此, MNW 方程的研究可以進一步加深對方程(1)的認識. MNW 方程最初由Mikhauilov、Novikov 和 Wang 通過對稱的方法給出，并且他們證明了該方程具有 bi-Hamilton 結構和遞歸算子. 通過考慮一個 3×3 的矩陣譜問題, 文獻[5] 給出了方程 (2) 的一個零曲率表示, 但并未考慮其相應的方程族與守恒率等可積系統的相關問題. 文獻[6]考慮了 MNW 方程的相應 Lie 代數，得到了 Lie 代數結構下的方程族及 bi-Hamilton 結構, 但是沒有給出方程的無窮守恒律. 本文從零曲率方程出發, 得到了顯式的 V 的表示、局部遞歸算子和方程的無窮多守恒律. 這些性質的取得為考慮方程的顯式解提供了思路和工具[7-8].

本文通過探討與 3×3 矩陣譜問題相聯系的零曲率方程，推導出 MNW 方程族，然后借助于該 3×3 矩陣譜問題, 給出該方程族的 bi-Hamilton 結構和方程 (2) 的無窮多守恒律. 本文通過引入Lenard遞歸方程, 得到了零曲率方程的解的表示,并借助于跡恒等式給出了 MNW 方程族的廣義 bi-Hamilton 結構. 通過考慮與方程 (2) 相關的兩個線性譜問題，得到了 (2) 式的無窮多守恒律.

1 Mikhauilov-Novikov-Wang方程族

推導與如下 3×3 矩陣譜問題相聯系的 MNW方程族

(3)

其中：u,v為位勢；λ為常值譜參數. 為了推導相應的非線性演化方程族, 引入兩個Lenard遞歸方程:

(4)

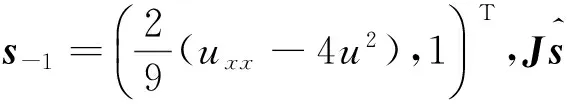
(5)

(6)

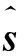
現在來求解駐定零曲率方程

(7)

該方程等價于

V11,x-V21+uV12+(λ+λ-1v)V13=0；V12,x+V11-V22+uV13=0；V13,x+V12-V23=0；

V21,x+u(V22-V11)-V31+(λ+λ-1v)V23=0；V22,x+V21+uV23-uV12-V32=0；

V23,x-uV13-V33+V22=0；V31,x+(λ+λ-1v)(V33-V11)+u(V32-V21)=0；

V32,x-(λ+λ-1v)V12+u(V33-V22)+V31=0；V33,x-(λ+λ-1v)V13+V32-uV23=0.

(8)

其中:

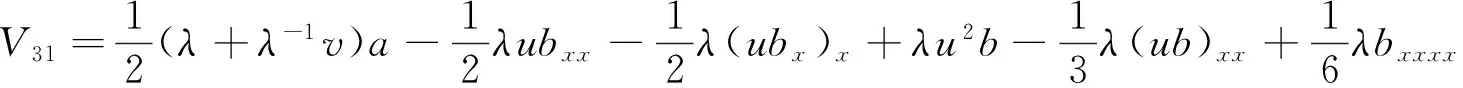
(9)

KSj-1=JSj,j≥0,JS-1=0,

(10)

其中Sj=(aj,bj)T. 因方程JS-1=0的通解為

(11)

則由

(12)

定義的函數Sj滿足遞歸方程(10), 其中:α0、β0為任意常數.

假設ψ滿足譜問題式(3) 和如下的輔助譜問題

(13)

(14)

該族非線性演化方程中第一個非平凡的方程為

(15)

如果令α0=9，β0=0，t0=t, 式(15)恰為要研究的方程 (2).

2 廣義bi-Hamilton結構

本節將通過跡恒等式來獲得式 (14) 的廣義bi-Hamilton結構[9-10]，其中跡恒等式為

先計算以下量

(16)

跡恒等式

(17)

其中γ為待定常數, 比較(17)式中λ同次冪的系數可以得到

(18)

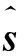
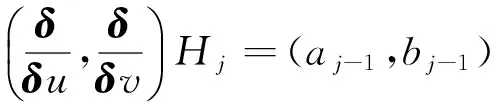
(19)

(20)

3 無窮多守恒律

Φxx+3ΦΦx+Φ3-2uΦ=λ+λ-1v+ux.

(21)

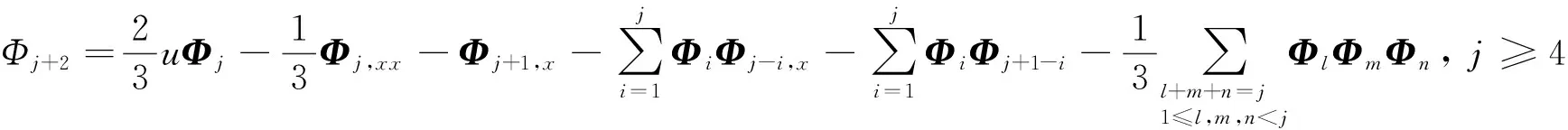
(22)

從輔助譜問題(13)式可得

(23)

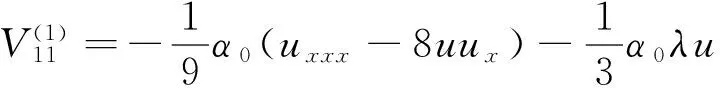
(24)

如果同時把θ展開成λ的級數形式

(25)

從而可得θj的如下表示

(26)

具有多Hamilton結構或無窮多守恒量都是孤子方程可積的重要特征，利用依賴于譜參數的守恒密度的積分在約束條件下求泛函導數的方法可知，無窮多Hamilton泛函與無窮多守恒量之間具有一一對應的關系[11].

[1] KAUP D J. On the inverse scattering problem for cubic eigenvalue problems of the classψxxx+6Q(x)ψx+6R(x)ψ=λψ[J]. Stud Appl Math, 1980, 62(3): 189-216．

[2] KUPERSHMIDT B A. A super Korteweg-De Vries equation: an integrable system [J]. Phys Lett A, 1984, 102(5/6): 213-215．

[3] GENG X G, WU L H, HE G L. Quasi-periodic solutions of the Kaup-Kupershmidt hierarchy [J]. Nonlinear Sci, 2013, 23(4): 527-555．

[4] MIKHAILOV A V, Novikov V S, Wang J P. On classification of integrable nonevolutionary equations [J]. Stud Appl Math, 2007, 118(4): 419-457.

[5] SERGYEYEV A. Zero-curvature representation for a new fifth-order integrable system[J]. Math Sci, 2008, 151(4): 3227-3229．

[6] SHAN X Y, ZHU J Y. The Mikhauilov-Novikov-Wang hierarchy and its Hamiltonian structures [J]. Acta Phys Polonica B, 2012, 43(10): 1953-1963．

[7] 何國亮，楊本朝．擾動Korteweg-de Vries方程的Darboux變換及其顯式解[J]. 鄭州大學學報(理學版)，2012，44(3)：4-7．

[8] 李雪梅，牛虧環． 廣義 TD 族及一些非線性演化方程的顯式解[J]. 鄭州大學學報(理學版)，2007, 39(3)：1-6．

[9] TU G Z. On Liouville integrability of zero-curvature equations and the Yang hierarchy [J]. J Phys A Math Gen, 1989, 22(13): 2375-2392．

[10]HE G L, GENG X G. An extension of the modified Sawada-Kotera equation and conservation laws [J]. Chin Phys B, 2012, 21(7): 070205．

[11]王燕. 一類孤立子系統的無窮守恒率及Hamilton結構[D]. 鄭州：鄭州大學，2006．

(責任編輯：方惠敏)

The Mikhauilov-Novikov-Wang Hierarchy,the bi-Hamiltonian Structures and the Conservation Laws

HE Guoliang1， ZHANG Yongsan2

(1.SchoolofMathematicsandInformationScience,ZhengzhouUniversityofLightIndustry,Zhengzhou450002,China; 2.DepartmentofHumanitiesandArtDesign,HenanMechanicalandElectricalVocationalCollege,Zhengzhou451191,China)

The Mikhauilov-Novikov-Wang hierarchy which associated with a 3×3 matrix spectral problem was proposed with the help of the zero-curvature equation. By using the trace identity and two skew-symmetric operators, the bi-Hamiltonian structures of the hierarchy were established. The infinite many conservation laws of the Mikhauilov-Novikov-Wang equation were obtained from two linear spectral problems.

Mikhauilov-Novikov-Wang hierarchy；bi-Hamiltonian structure；conservation laws

2015-11-16

國家自然科學基金資助項目(11501526)；鄭州輕工業學院博士基金資助項目(2013BSJJ051)．

何國亮(1983—)，男，河南鄭州人，副教授，博士，主要從事孤立子與可積系統研究，E-mail：glhemath@163.com；通訊作者：張永三(1982—)，男，河南平頂山人，講師，碩士，主要從事孤立子與可積系統研究，E-mail：zyslcczzy@126.com．

何國亮，張永三．Mikhauilov-Novikov-Wang方程族及其bi-Hamilton結構與守恒律[J]．鄭州大學學報(理學版)，2016，48(2)：1-4.

O175

A

1671-6841(2016)02-0001-04

10.13705/j.issn.1671-6841.2015263