基于ARMA模型和狼群算法的陀螺隨機漂移建模研究*

來凌紅

(武警后勤學院 軍交運輸系，天津 300309)

基于ARMA模型和狼群算法的陀螺隨機漂移建模研究*

來凌紅

(武警后勤學院 軍交運輸系，天津 300309)

摘要:光纖陀螺的隨機漂移誤差是影響慣性導航系統精度的關鍵因素之一，根據陀螺隨機漂移數據的數學模型進行補償，可有效地提高系統精度。在大量實驗的基礎上建立陀螺隨機漂移的自回歸移動平均(ARMA)模型，同時使用長自回歸模型法求解模型參數，再對參數進行優化。實驗結果證明:經狼群算法優化后的陀螺隨機漂移模型更加準確，建模精度相對于傳統的時間序列分析法有了較大提高。研究內容對光纖陀螺隨機漂移建模精度的提高有較好的參考價值。

關鍵詞:陀螺隨機漂移； 自回歸移動平均模型； 狼群算法； 參數優化

0引言

自回歸移動平均(ARMA)模型是陀螺漂移常用模型之一，具有較高的工程應用價值[1～3]。其中以線性化參數計算為求解方法的長自回歸法在該模型建模中應用較為廣泛，但其在求解過程中對模型參數的非線性估計轉化成對參數的線性估計，因此，在求解過程中存在線性誤差，降低模型參數的精度。

文獻[4]根據狼群群體智能行為，深入分析狼群捕食行為及其獵物的不同分配方式，人工模擬出游走、召喚、圍攻等3種智能行為，繼而提出狼群算法(wolfpackalgorithm,WPA)。與蟻群算法、蜂群算法、魚群算法等算法相比，狼群算法具有較好的全局收斂性與計算魯棒性，同時可直接用于求解目標函數的優化問題。本文利用狼群算法對光纖陀螺(FOG)隨機漂移模型的參數進行優化，其建模效果與長自回歸法相比,模型精度有較大幅度的提升。

1陀螺隨機漂移模型

光纖陀螺的漂移分為系統性漂移與隨機性漂移兩種，其中前者通過測試即便對標定進行補償，精度的提高也是有限的；而后者隨時間連續性變化，是量化陀螺漂移誤差的重要指標之一，同時對慣性導航系統的精度有較大的影響[5～7]。因此，建立盡可能精確的陀螺隨機漂移模型，對其工作狀態進行估計后進行補償，可有效降低光纖陀螺隨機漂移對慣性導航系統精度的影響。

1.1ARMA模型

陀螺隨機漂移模型通常使用ARMA(n,m)模型，具體表達式為

(1)

式(1)反映了響應數據序列xt與歷史輸入值xt-k的對應關系。等式的左邊是自回歸差分多項式AR模型，其階次為n；右邊是滑動平均差分多項式MA模型，其階次為m。ak,bh分別表示待識別的自回歸系數與滑動均值系數，eh為殘差，{eh}序列為白噪聲激勵，同時,當k=0時，令a0=b0=1。

ARMA(n,m)模型要求樣本數據滿足正態、平穩與零均值的條件，故模型建立前要對數據序列進行上述驗證。對不符合條件的時間序列進行零均值化與差分處理使其滿足上述要求，然后利用時間序列分析法進行模型的擬合求解。

1.2長自回歸模型計算殘差

長自回歸法的基本原理:當對同一個隨機過程進行分析時，同一觀測時序{xt}建立的ARMA(n,m)模型、AR(n)模型和MA(m)模型都是等價的數學模型，三者具有相等的傳遞函數，而且在同一時刻的殘差相等。根據這一基本原則，先對AR(n)模型參數進行求解，再根據傳遞函數相等的關系估計出ARMA(n,m)模型的參數。

根據上述思路，本文使用最小二乘估計法求解AR(n)模型參數，由多元回歸理論可知，參數ak矩陣的最小二乘估計如下

(2)

式中

y=[xn+1xn+2…xN]

(3)

ak=[a1a2…an]

(4)

(5)

ARAM模型參數的估計，使用長自回歸模型法。參數ak矩陣的最小二乘估計為

ak=-bnIn-m-…-b2In-2-b1In-1+In

(6)

先估計出AR模型，再通過傳遞函數相等的關系對ARMA模型的參數ak與bh進行求解。計算關于ak的線性方程組

(7)

關于bh的線性方程組

(8)

2狼群算法

狼群算法以人工狼為主體，使用基于不同職責分工與自下而上的合作式搜索方法求解最優化問題。基本思路：隨機產生N匹人工狼，隨機分布在待優化參數的可行域內。選取最優人工狼為頭狼，部分探狼執行隨機游走行為，同時判斷感知到的獵物的氣味yi。當yi≥ylead時，則頭狼發出召喚行為，周圍的狼聽到頭狼的嚎叫后以較大的步長朝頭狼所在的位置奔襲，對獵物進行圍攻。最后狼群按照“勝者為王”的頭狼產生機制對頭狼所在位置進行更新，當滿足終止條件時，輸出頭狼位置，即優化問題的最優解。WPA算法流程圖如圖1。

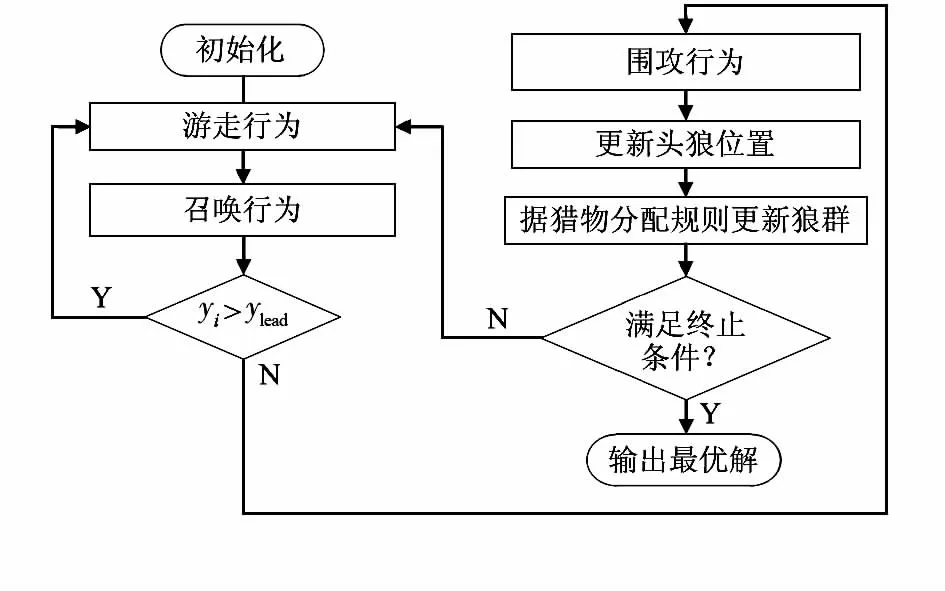
圖1　狼群算法流程圖Fig 1　Flow chart of WPA

3陀螺隨機漂移的狼群算法建模

首先通過長自回歸法求解出ARMA模型參數，然后使用狼群算法對模型參數進行優化，具體步驟如下：

1)設置人工狼的個數N，最大迭代次數M，距離判定因子w=500，更新比例因子β=6。

4)選取最優人工狼為頭狼，除頭狼外最佳位置的S匹人工狼為探狼，按照式(9)進行游走行為

(9)

若某只探狼偵查到獵物氣味濃度yi大于頭狼感知的濃度ylead，轉步驟(5)。

5)人工猛狼根據式(10)向獵物奔襲

(10)

當猛狼感知的獵物氣味濃度yi≤ylesd時，則yi>ylead，代頭狼發起召喚行為；否則，繼續奔襲，轉步驟(6)。

6)按式(11)對參與圍攻行為的人工狼位置進行更新，同時發起圍攻行為

(11)

按“勝者為王”的頭狼產生機制，對頭狼位置進行更新，轉步驟(7)。

7)判斷是否達到目標函數要求的優化精度或最大迭代次數，若是，輸出頭狼位置，也就是問題的最優解；否則，轉步驟(4),繼續循環。

4模型求解與結果分析

4.1數據消噪預處理

陀螺隨機漂移的小波消噪與預處理方法利用陀螺漂移數據進行建模時，首先要對數據進行消噪和預處理。提高建模數據的有效性，以獲取平穩、正態、零均值的序列,保證樣本數據的準確性[8]。建模所用的數據為國外進口光纖陀螺室溫下的靜態輸出數據，采樣頻率為200 Hz，測試時間10 min,獲取測量數據列{xt}。前6 min數據作為建模基礎數據，后4 min數據用于模型檢驗。數據平穩化處理的步驟如下:

1) 首先進行剔點、平滑處理。實際測得FOG漂移序列一般為非平穩序列，因此，剔除異常點后必須進行平穩化處理，同時去除趨勢項。

2) 如果去除趨勢項后的序列仍為非平穩時間序列,則應進行差分處理,直至獲取平穩時間序列，一般情況下至少進行二階差分處理。

3) 經過上述處理后的時間序列{xt}作為預測模型的訓練與測試樣本，如圖2。

圖2　陀螺實測漂移Fig 2　Actually measured drift of FOG

4.2模型建模結果

長自回歸建模結果ARMA(n,m)模型

x(t)-0.286 0x(t-1)-0.095 6x(t-2)=

e(t)+0.881 5e(t-1).

(12)

模型仿真漂移預測數據與實測數據對比圖如圖3。

圖3　長自回歸法預測漂移與陀螺實測漂移Fig 3　Predicted drift by long AR method and actually measured drifts by gyro

圖4　狼群算法迭代曲線Fig 4　Iterative curve of WPA

由上圖分析可知，約經36次迭代后，擬合殘差的方差收斂到最優，同時經參數優化后的ARMA(2,1)模型

x(t)-1.462 8x(t-1)+0.596 3x(t-2)=

e(t)-0.540 6e(t-1).

(13)

模型仿真漂移預測數據與實測數據對比圖如圖5。

圖5　優化模型預測漂移與陀螺實測漂移Fig 5　Optimized model predicted drift and actually measured drift by gyro

經上述結果分析，經狼群算法優化后的ARMA(n,m)模型與使用長自回歸模型求解的ARMA(n,m)模型相比，e(t)序列的方差減小11.62 %。

5結論

本文首先用傳統的長自回歸模型法建立光纖陀螺隨機漂移的ARMA(n,m)模型，然后通過狼群算法對該模型參數進行優化。實驗結果顯示:優化后的模型減小了長自回

歸模型法所帶來的非線性誤差。本方法對抑制陀螺隨機漂移誤差具有較好的參考價值。

參考文獻:

[1]Salarieh H,Alasty A.Chaos synchro nization of nonlinear gyros in presence of stochastic excitation via sliding mode control [J].Journal of Sound and Vibration,2008,313(3-5):760-771.

[2]Xiong Jian,Liu Jianye,Lai Jizhou,et al.Identification approach for gyroscope AEIMA model based on Gaussian particle fil-ter[J].Journal of Chinese Inertial Technology,2010,18(4):493-497.

[3]Hasan M K,Hossain N M,Naylor P A.Autocorrelation model based identification method for ARMA system in noise[J].IEE Proc Vision Image Signal Process,2005,152(5):520-526.

[4]吳虎勝，張鳳鳴，吳廬山.一種新的群體智能算法——狼群算法[J].系統工程與電子技術,2013，35(11):2430-2438.

[5]Kaderli A,Kayhan A S.Spectral estimation of ARMA processes using ARMA-cepstum recursion[J].IEEE Signal Processing Letters,2000,7(9):259-261.

[6]翟恒昂，朱家海，吳訓忠，等.基于小生境蟻群算法的陀螺隨機漂移建模方法研究[J].計算機測量與控制,2013,21(5):1327-1329.

[7]楊慶輝，杜紅英乙，陳雄,等.微機電陀螺隨機漂移建模與卡爾曼濾波[J].計算機仿真，2015,32(3):68-72.

[8]孔慶鵬，高爽，林鐵，等.基于ANF的激光陀螺消噪處理研究[J].傳感器與微系統，2009,28(1):18-21.

ResearchongyroscoperandomdriftmodelingbasedonARMAmodelandwolfpackalgorithm*

LAILing-hong

(DepartmentofMilitaryTransportation,LogisticsUniversityofPeople’sArmedPoliceForce,Tianjin300309,China)

Abstract:Random drift error of fiber-optic gyroscope(FOG) is one of the key factors that affect precision of inertial navigation system(INS),and precision of INS can be effectively improved by compensating according to math model for datas of FOG random drift.Auto regressive moving average(ARMA) model for gyro random drift is established on the basis of large numbers of experiments,meanwhile,method of long auto regressive model is used to solve model parameters,and optimize parameters.Experimental results prove that the FOG random drift model optimized by wolf pack algorithm(WPA) is more accurate.Compared with traditional method of time series analysis,modeling precision is increased greatly.The method has a better reference value for improving precision of FOG random drift modeling.

Key words:gyroscope random drift; ARMA model; wolf pack algorithm(WPA); parameter optimization

DOI:10.13873/J.1000—9787(2016)04—0056—03

收稿日期：2015—08—31

*基金項目：聯合實驗室開放基金資助項目(FOM2015OF015)；武警總部后勤部課題資助項目

中圖分類號:TP 274; V 241

文獻標識碼:A

文章編號:1000—9787(2016)04—0056—03

作者簡介:

來凌紅(1972-)，男，湖北公安人，碩士，副教授，主要研究領域為機電一體化、電氣系統。