基于BDS/GLONASS的短基線單歷元多頻RTK定位研究

謝建濤　郝金明　于合理　田英國

1　信息工程大學導航與空天目標工程學院，鄭州市科學大道62號，450001

?

基于BDS/GLONASS的短基線單歷元多頻RTK定位研究

謝建濤1郝金明1于合理1田英國1

1信息工程大學導航與空天目標工程學院，鄭州市科學大道62號，450001

摘要：在基于幾何的TCAR(three carrier ambiguity resolution)算法基礎上，將BDS/GLONASS組合引入到寬巷和窄巷模糊度解算中，提出一種基于雙系統組合的單歷元多頻RTK定位模型，并通過實驗進行分析。結果表明，相比于其他模型，該模型在模糊度解算效率和定位精度方面都是最優的。

關鍵詞：BDS/GLONASS；TCAR；多頻RTK；模糊度解算

GNSS單歷元RTK定位的精度和可靠性取決于模糊度能否正確固定[1]。在GNSS單系統條件下，當天空中的可見導航衛星數過少時，整周模糊度的計算無法完成。2011-12-31 GLONASS 恢復全球組網運行；2012年底，我國的北斗衛星導航系統具備了向中國及周邊地區提供服務的能力。多個衛星導航系統的投入運行，增加了導航衛星的可見數，有利于RTK整周模糊度的解算。

基于三頻觀測的TCAR(three carrier ambiguity resolution)算法按波長從長到短依次固定超寬巷、寬巷和窄巷模糊度，可明顯提高模糊度解算的效率。文獻[2-3]結合GPS數據對TCAR算法進行優化；文獻[4]采用TCAR算法對BDS單歷元RTK定位的性能進行研究；文獻[5-7]對GPS/GLONASS聯合定位的數據處理模型進行了研究。目前針對BDS/GLONASS組合的RTK定位研究還不多。本文在基于幾何的TCAR算法基礎上，對BDS/GLONASS組合單歷元多頻RTK定位的數學模型進行研究，并結合實驗數據進行分析。

1時間與坐標系統的統一

時間系統和坐標系統是導航定位的參考基準，任何形式的導航定位都必須在一定的時間和坐標框架內進行[8]。BDS時間基準采用北斗時(BDT)，BDT采用國際單位制(SI)s為基本單位連續累計，起始歷元為2000-01-01 UTC 00:00 00，采用周和周內秒計數。BDT通過UTC(NTSC)與國際UTC建立聯系，與UTC的偏差保持在100 ns以內：

BDT=UTC+1s×n

(1)

GLONASS時間(GLONASST)屬于UTC時間系統，與俄羅斯維持的協調世界時UTC(SU)存在 3 h的整數差:

GLONASST=UTC(SU)+3h

(2)

通過對BDS、GLONASS時間框架的分析可知，將UTC作為中間變量，可實現不同時間系統的統一。實際上，目前許多GNSS混合觀測文件包含了多個系統的數據，且統一采用GPST作為觀測時間系統，因此，這部分轉換通常可省去。

最新的PZ90.02與 ITRF2000只存在原點的平移，3個軸的定向與 ITRF一致。PZ90.02與 ITRF2000的轉換關系為[8]：

(3)

CGCS2000定義為 ITRF97，采用 2000.0歷元下的坐標和速度場。CGCS2000與PZ90都與ITRF存在一定的關系，它們之間的轉換本質上是在不同的ITRF框架間實現的。文中雙差觀測方程的建立是基于各系統內部的，系統之間不作差，可有效避免不同系統間存在的系統性偏差對解算結果造成的不利影響。

2BDS/GLONASS組合差分定位模型

在短基線(小于20 km)條件下，忽略雙差對流層殘差、雙差電離層殘差以及軌道誤差的影響，載波和偽距差分定位的數學模型見文獻[9]。雙差模糊度浮點解到固定解的計算采用LAMBDA算法。

3多頻模糊度解算

三頻情形下，頻率的多樣性可以提高無幾何模糊度解算的可靠性。無幾何條件下，觀測噪聲和電離層延遲誤差對窄巷模糊度解算造成的影響非常敏感，影響模糊度解算的收斂速度和可靠性。因此，對于多系統多頻情形，基于整數最小二乘估計的幾何模糊度解算可以將模糊度固定成功率最大化，是模糊度解算的第一選擇[9]。本文在幾何模型的基礎上，提出基于GLONASS雙頻數據和BDS三頻數據的多頻模糊度解算(mulitple carrier ambiguity resolution，MCAR)算法。

3.1超寬巷(EWL)模糊度解算

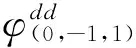
(4)

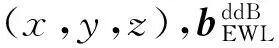
3.2寬巷(WL)模糊度解算

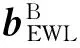
采用GLONASS雙頻數據與BDS三頻數據組合定位時，WL12載波的雙差觀測方程為：

(5)

3.3窄巷(NL)模糊度解算

采用GLONASS雙頻數據與BDS三頻數據組合定位時，NL載波的雙差觀測方程為：

(6)

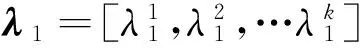
第一步中，EWL組合觀測量φ(0,-1,1)具有長波長、低噪聲、低電離層延遲的優點。研究表明，采用偽距觀測量輔助固定φ(0,-1,1)模糊度參數N(0,-1,1)的成功率極高，短基線單歷元條件下可達100%。

第二步中，WL模糊度估計采用直接取整的方式，成功率較低，導致最終估計的可靠性不高。因此，在第二步中固定WL模糊度時采用基于幾何的觀測模型，使用接收機與衛星之間的空間幾何約束信息。由于顧及所有觀測量信息和模糊度之間的相關信息，該算法優于無幾何模型。

EWL和WL模糊度解算采用經典最小二乘估計法，短基線條件下其固定成功率非常高。相比于BDS/GLONASS組合直接解算窄巷模糊度，MCAR算法兼具TCAR算法的優點，通過對原始載波相位觀測量進行線性組合，得到長波長、弱電離層延遲、弱觀測噪聲的最優虛擬觀測量。按波長從長到短，采用不斷精化的偽距觀測量依次固定EWL、WL和NL模糊度，可明顯提高NL模糊度解算的效率。

4實驗分析

為驗證MCAR模型的有效性和可行性，采用兩組靜態基線數據進行實驗。數據采集使用司南多模接收機，衛星高度截止角設為15°(表1)。

將GLONASS雙頻數據與BDS三頻數據組合直接解算NL記為BDS/GLONASS模型，與MCAR模型就模糊度解算和定位精度兩個指標進行比對。解算過程均采用單歷元模糊度固定模式，其優點是解算結果不受載波相位周跳的影響。圖1中EWL和WL模糊度固定ratio閾值rE和rW均設為2，NL模糊度固定ratio閾值rN分別設為2、3和5，以比較BDS/GLONASS和MCAR不同模式下NL模糊度解算(ambiguity resolution,AR)的效率。由于EWL或WL模糊度固定失敗都會造成NL模糊度無法解算，因此本文只需對NL模糊度解算效率進行比較。統計結果見表2和表3。

由表2可以看出，對于8 m超短基線，ratio閾值為2時，MCAR模型和BDS/GLONASS模型NL模糊度固定的成功率都達到100%；當閾值分別為3和5時，前者的ratio值分布要優于后者。

由表3可以看出，即使對于長度為8 km的基線，忽略電離層殘差的影響，當ratio閾值為3時，MCAR模糊度固定成功率依然高于99%，優于BDS/GLONASS模型。當嚴格執行ratio閾值為2時，由于MCAR模型兼具TCAR算法與多系統組合的優點，因此其模糊度固定成功率是最高的。總體來看，對于8 km長的基線，雙差電離層延遲殘差使得BDS/GLONASS組合直接固定NL模糊度變得困難；對于MCA模式，通過不斷精化偽距觀測量，對EWL、WL和NL模糊度依次逐級固定，可保持較高的NL固定率，優于BDS/GLONASS模式。

ratio閾值為2時，對未得到NL固定解的歷元，當其浮點解與參考位置在東向和北向上的偏差小于0.1 m，在天頂向的偏差小于0.2 m時，認為其模糊度固定解被錯誤地拒絕而未被采納。對數據集進行統計，得到表4和表5。

由表4可知，ratio閾值為2時，對于數據集A，兩種模式下模糊度固定的錯誤拒絕率均為0，即沒有出現解算正確卻未得到固定解的情況。表5中，對于數據集B，兩種模式下未得到固定解但解算正確的歷元數依次為202和0。MCAR模型的錯誤拒絕率僅為0.32%，遠低于BDS/GLONASS模型。這是因為，對于8 km的基線，雙差電離層延遲殘差使得BDS/GLONASS模式NL模糊度固定效率降低，而MCAR模式能在一定程度上彌補這一缺陷。因此，MCAR模型的模糊度解算的可靠性更高，效果更優。

ratio閾值為2時，針對所有得到固定解的歷元，將其解算得到的位置參數與參考位置作差，得到其在東、北、天3個方向的偏差，見圖2～7。

由圖2～4可知，對于8 m超短基線，兩種模型在東向和北向的定位誤差保持在1 cm以內，天頂方向的定位誤差保持在2 cm以內。圖5～7中，對于數據集B，隨著基線長度達到8 km，雙差電離層延遲殘差增大，忽略其影響時，這部分誤差會被位置參數吸收，造成BDS/GLONASS模型定位偏差波動較大，穩定性變差；而MCAR模式由于采用了模糊度得到固定的WL觀測量，模型結構更優，一定程度上削弱了這一影響。對所有得到固定解的歷元在不同方向上的定位偏差進行統計，得到表6。

由表6可以看出，對于數據集A，東向上TCAR和BDS/GLONASS模型定位RMS相近，分別為0.20 cm和0.19 cm；北向和天頂方向上，MCAR模型定位RMS分別為0.14 cm和0.44 cm，均優于BDS/GLONASS模型。對于數據集B，MCAR模型在各方向上的定位RMS是最小的，效果最優。總體而言，MCAR模型的定位效果優于BDS/GLONASS模型。

5結語

本文借鑒多系統組合定位和TCAR模型的優點，提出基于雙系統組合的MCAR算法。結合實測數據，就模糊度解算效率和定位精度兩個指標進行驗證分析，結果表明，本文提出的MCAR模型是可行的。

參考文獻

[1]Deng C L, Tang W M, Liu J N, et al. Reliable Single-Epoch Ambiguity Resolution for Short Baselines Using Combined GPS/Beidou System[J].GPS Solutions, 2013, 17(2): 126-132

[2]李博峰,沈云中,周澤波.中長基線三頻GNSS模糊度的快速算法[J].測繪學報,2009,38(4):296-301(Li Bofeng, Shen Yunzhong, Zhou Zebo.A New Method for Medium and Long Range Three Frequency GNSS Rapid Ambiguity Resolution[J]. Acta Geodaetica et Cartographica Sinica,2009,38(4):296-301)

[3]范建軍，王飛雪. 一種短基線GNSS的三頻模糊度解算(TCAR)方法[J]. 測繪學報，2007，36(1)：43-49( Fan Jianjun,Wang Feixue. A Method for GNSS Three Frequency Ambiguity Resolution Based on Short Baselines[J]. Acta Geodaetica et Cartographica Sinica,2007,36(1)：43-49)

[4]Tang W M, Deng C L, Shi C,et al.Triple-Frequency Carrier Ambiguity Resolution for Beidou Navigation Satellite System[J].GPS Solutions, 2014, 18(3):335-344

[5]高星偉，李毓麟，葛茂榮.GPS/GLONASS相位差分的數據處理方法[J].測繪科學,2004,29(2):22-28(Gao Xingwei,Li Yulin,Ge Maorong.Processing Approach in Combined GPS/GLONASS Positioning[J].Science of Surveying and Mapping,2004,29(2):22-28)

[6]Duan J J，Shen Y Z．GPS/GLONASS Combined Point Positioning Using Variance Component Estimation [J]．Bulletin of Surveying and Mapping, 2011, 40(4):4-6

[7]Shi X Y, Yuan B Y, Bao Z X. Research and Implementation of Ambiguity Resolution for Combined GPS/GLONASS/COMPASS Positioning[C].China Satellite Navigation Conference (CSNC) 2013, 2013

[8]李鶴峰,黨亞民,秘金鐘,等.BDS與GPS、GLONASS多模融合導航定位時空統一[J].大地測量與地球動力學，2013,33(4)：73-78(Li Hefeng,Dang Yamin,Bei Jinzhong,et al.Research on Spatio Temporal Unification of BDS/GPS/GLONASS Multi-Mode Fusion Navigation and Positioning[J].Journal of Geodesy and Geodynamics,2013,33(4)：73-78)

[9]李金龍. 北斗/GPS多頻實時精密定位理論與算法[D].鄭州:信息工程大學,2014 (Li Jinlong. BDS/GPS Multi-Frequency Real-Time Kinematic Positioning Theory and Algorithms[D].Zhengzhou:Information Engineering University,2014)

About the first author:XIE Jiantao,PhD candidate, majors in multi-system and multi-frequency RTK positioning theory and algorithms,E-mail: xiejiantao0911@sina.com.

Research on Single-Epoch and Multi-Frequency BDS/GLONASS RTK Positioning for Short Baseline

XIEJiantao1HAOJinming1YUHeli1TIANYingguo1

1School of Navigation and Space Target Engineering, Information Engineering University, 62 Kexue Road,Zhengzhou 450001,China

Abstract:In this paper, considering the geometric TCAR (three carrier ambiguity resolution) algorithm, BDS/GLONASS mode is brought into wide lane and narrow lane calculation. Then the model of single epoch and multi-frequency BDS/GLONASS RTK positioning is presented. The mathematical model and its feasibility are verified with the measured data, and the result shows that compared with other models, the proposed model is optimal in ambiguity resolution efficiency and positioning accuracy. Key words: BDS/GLONASS;TCAR;RTK of multi-systems;ambiguity resolution

收稿日期：2015-05-19

第一作者簡介：謝建濤 ，博士生 ，主要從事GNSS多系統多頻實時精密定位理論與算法研究，E-mail：xiejiantao0911@sina.com。

DOI：10.14075/j.jgg.2016.06.014

文章編號：1671-5942(2016)06-0529-05

中圖分類號：P228

文獻標識碼：A