基于黃金三角形的創意折疊桌設計

陳貴靖，黃景偉，李 銳

(四川理工學院 四川自貢643000)

基于黃金三角形的創意折疊桌設計

陳貴靖，黃景偉，李 銳

(四川理工學院 四川自貢643000)

根據黃金比例的美觀要求，研究了創意平板折疊桌的設計。通過應用黃金等腰三角形原理，采用幾何關系方法，對平板折疊桌的木條長度、最外側齒輪長度、桌角邊緣線的描述、開槽長度、折疊桌的動態變化過程等工藝參數進行了探討。經過算法設計、參數修正，利用MATLAB軟件編程獲得并實現了平板折疊桌工藝參數，得到創意平板折疊桌的可視化模型，既滿足了客戶需求又實現了設計美觀、符合標準。

創意折疊桌 黃金等腰三角形 幾何關系 工藝參數 可視化模型

0 引 言

隨著生活水平質量的提高，簡潔大方、功能多樣、更能合理安排空間的生活創意作品深受人們的喜愛。2011年，荷蘭設計師Robert van Embriqs設計了一種美觀的創意平板折疊桌，不僅能滿足人們的創意生活需求，還能極大地提升運輸效率，方便家居收納。本文設計了折疊桌的加工參數(木條數、桌腿木條長度、邊緣曲線描述、旋轉角度、開槽長度等)，并實現了可視化。

1 設計工藝參數

1.1 建立坐標系

以桌面圓心作為坐標系原點O，以木板長為X軸，以木板寬為Y軸，取垂直于平面XOY并且過原點O的線作為Z軸。

1.2 桌腿木條長度的計算

1.2.1 確定桌腿木條條數

設定木板的長度為L、寬度為X、厚度為Y，木條寬度為Z。則木板寬的兩邊木條數均為：

1.2.2 確定桌腿木條長度

1.2.2.1 確定折疊桌中間木條長度

將木板分為N個木條，規定棱最短的木條為中間木條。

1.2.2.2 桌腿最外側木條長度的確定

式中：h為桌子高度，則折疊桌最外側的鋸齒長度W為：

式中：L為木板的長。

1.3 桌腿邊緣點邊緣曲線的數學描述

設定第i個桌腿邊緣點的坐標為Pi( xi, yi, zi)，該桌腿的旋轉點為Qi( xi, yi, o)，連接PiO，過點Qi作垂直于桌面直徑并交于點Mi(xi, yi, o)，PiO=l，QiPi=di，QiO=ri，∠OQiPi=θi1，∠OQiM=θi2，∠PiQiM=θi3。

點Pi在平面XOY投影在線QiMi上點Ni，所以線段QiPi在平面XOY上投影線為線QiM上的一段，則有PiNi⊥平面XOY、QiO?平面XOY、QiNi?平面XOY。

綜上所述，線QiPi, QiO, PiO兩兩之間的夾角滿足三余弦定理：[4]

1.4 折疊桌動態的分析

1.4.1 折疊桌旋轉原理分析

在折疊桌的轉動過程中，起主導作用的是最外側的4根木條，即4根支撐桌腿。支撐腿的轉動通過鋼筋軸傳動到里面的木條，當支撐腿轉到預定位置時，里面的木條構成一條優美的弧線。本文從尋找支撐腿與里面木條旋轉角度間的關系展開分析。

1.4.2 邊角關系的確定

選取中間任意基準線li與最長基準線l，按照折疊桌旋轉原理旋轉(見圖1)，再對旋轉后的圖形進行側面投影，得到與圖2相似的圖形。

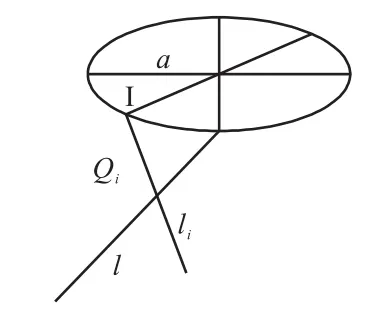
圖1 基準線旋轉后示意圖Fig.1 Baseline after rotation

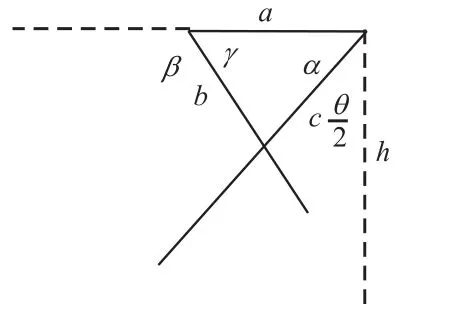
圖2 側面投影圖Fig.2 Side projection

圖2中a為第i個基準線和基準線l分別與圓桌的交點經過側面投影后的交點(即點Qi的X坐標值的絕對值)，h是折疊桌的高，b、c分別為圍城三角形的兩邊邊長，β為基準線轉過的角度，c為最長基準線l長的一半：d/2，Qi為第i個準基線的旋轉點。

根據上式(6)在基準線l旋轉α角度條件下計算得出結論：

①第i個基準線的鋼筋距旋轉點Qi的距離bi：

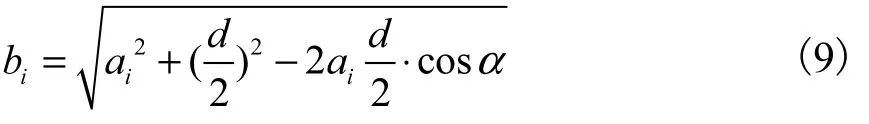
②第i個基準線的旋轉夾角iβ：

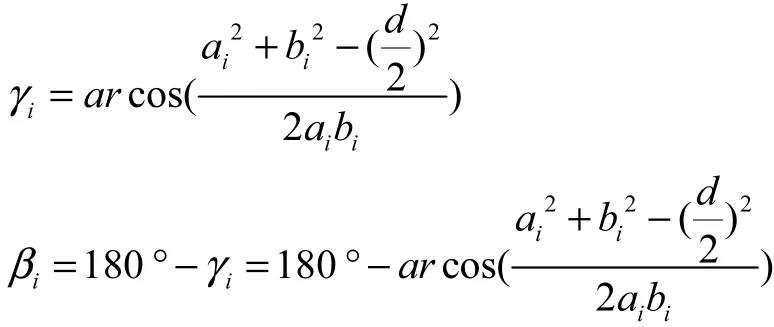
將公式(9)代入，進一步化簡得：

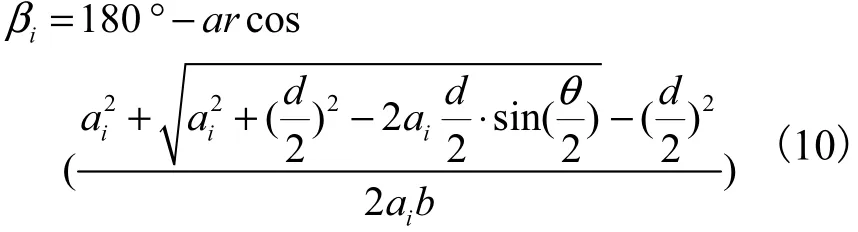
式中：i是基準線(木條)序號(i=2,3,…,n )，α的變化趨勢為90°→θmin/2=18°。

當α逐漸變化時，βi也會根據上式(7)中的關系而變化，即當最長桌腿木條轉動時，中間其他桌腿木條會一起接連轉動，從而形成一個動態變化過程。此動態變化過程可以根據角α的變化分度來確定動態變化的快慢。

1.5 桌腿木條開槽的計算

首先選定第i個桌腿木條底端作為該桌腿木條開槽的參考點。當桌腿木條未旋轉時，各個桌腿木條的鋼筋距離參考點最遠，為dmax；當桌腿木條旋轉至最大角度時，各個桌腿木條的鋼筋距離參考點最近，為dmin，則鋼筋距該木條的旋轉點Qi最遠為bimax。桌腿木條開槽的長度滿足以下關系：

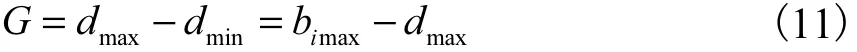
式中：G表示桌腿木條開槽長度。

2 實例應用

2.1 參數確定

給定平板折疊桌初始參數：平板尺寸為120,cm× 50,cm×3,cm，每根木條寬2.5,cm，連接桌腿木條的鋼筋固定在桌腿最外側木條的中心位置，折疊后桌子的高度為50,cm。

2.1.1 桌腿木條數及旋轉角度

木板的總桌腿木條數為40根，每一邊分別為20根桌腿木條；對最外側的木條結合美學觀念(等腰三角形的黃金角度)，以等腰三角形頂角θ=36°為基準，求出最外側桌腿木條的長度為52.6 cm，最外側的鋸齒長度為14.8,cm，此時對等腰三角形頂角θ修正為38.74°；根據折疊桌中間桌腿木條長度確定原則，得出中間桌腿木條的長度；最外側桌腿木條的旋轉最大角度也確定為70.63°，其他桌腿木條的最大旋轉動角度滿足公式(10)邊角關系，當在θ=38.74°時，得出內側各桌腿木條旋轉的最大角度。

2.1.2 各根桌腿木條開槽

當折疊桌未旋轉時，各個桌腿木條的鋼筋距離參考點最遠dmax=26.5cm ；當折疊桌旋轉至最大角度時，各桌腿木條的鋼筋距離參考點最近為dmin，則鋼筋距該木條的旋轉點Qi最遠為bimax，利用公式(8)計算出bimax。整個過程利用MATLAB軟件編程，求得每根桌腿開槽的長度(精確度0.000,1)。

2.1.3 桌腳邊緣線的數學描述

折疊桌旋轉點Q均在桌面邊線上，桌面邊線是半徑為r=25 cm的圓，所以QiO=ri=r=25cm，則：

式中：γi為第i個基準線與桌面的夾角，di為第i個基準線的長度。

2.2 動態分析

利用求得的各項參數，設定θ/2值從90°以1°為分度逐漸減小到θmin/2=19.34°，設定不同的變化分度，即可得到折疊桌的折疊動態變化過程。下面給出4個動態變化過程的示意圖，如圖3：

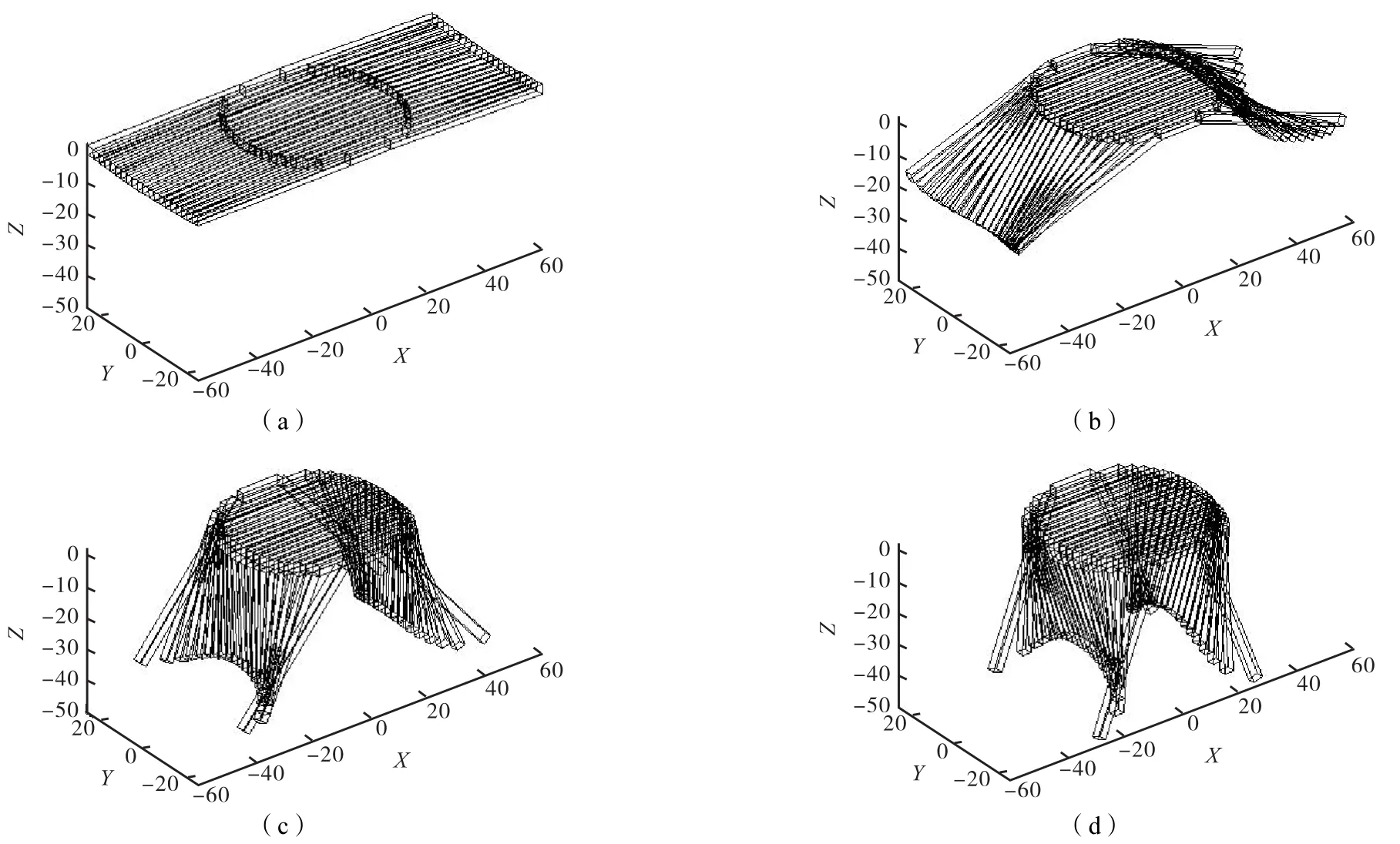
圖3 動態變化過程示意圖Fig.3 Schematic diagram of dynamic processes

在創意折疊桌動態變化過程示意圖中，圖3(d)為最終折疊桌可視化模型。

3 結 語

本文利用黃金比例確定了折疊桌的木條長度，并展開一系列設計加工參數的確定，對折疊桌進行了動態分析，最終使創意平板折疊桌不僅滿足客戶要求，還體現了美觀性。此方法可為創意折疊桌的設計人員提供借鑒。

［1］ 任立生. 設計心理學[M]. 2版，北京：化學工業出版社：2011.

［2］ 星小龍. 黃金三角應用舉例[J]. 青海教育，2007(5)：48.

［3］ 張雄. 黃金分割的美學意義及其應用[J]. 自然辯證法研究，1999(11)：5-9.

［4］ 高群安，崔雪陽. 三余弦公式推導及其應用[J]. 數理化學習：高中版，2013(7)：5-6.

Design of a Creative Folding Table Based on Golden Triangle

CHEN Guijing， HUANG Jingwei，LI Rui
(Sichuan University of Science & Engineering，Zigong City 643000，Sichuan Province，China)

According to aesthetic requirements of the golden ratio，a creative flat folding table was designed.With the application of gold isosceles triangle principle，technological parameters including strip length，length of the outer gear，description of table edge line，notching length，dynamic changing process of the folding table were studied using geometric relationships method.Through algorithm design and parameter modification，the parameters were obtained with the help of MATLAB and a visualization model of the table was realized，which not only meets customers’ demands but also the design standards and esthetic requirements.

creative folding table；golden triangle；geometry；process parameter；visualization model

TP399

：A

：1006-8945(2016)04-0062-03

2016-02-23