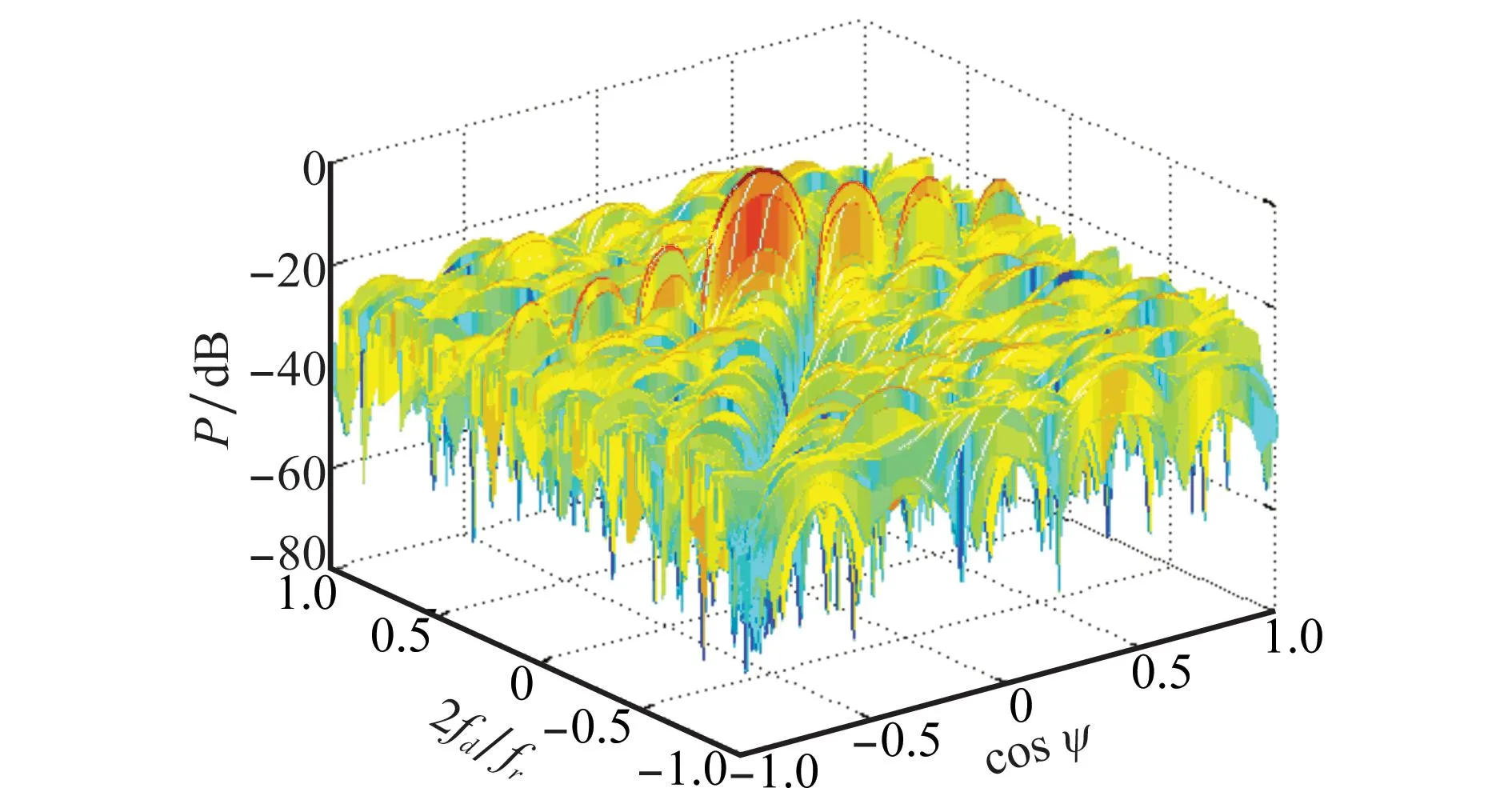
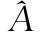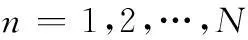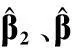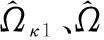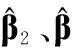基于CPT和RPF的空中高機動目標檢測與參數估計

李　海, 周　盟, 吳仁彪

(1. 中國民航大學天津市智能信號與圖像處理重點實驗室, 天津 300300;2. 澳大利亞伍倫貢大學電氣計算機與通信工程學院, 澳大利亞 伍倫貢 999029)

?

基于CPT和RPF的空中高機動目標檢測與參數估計

李海1,2, 周盟1, 吳仁彪1

(1. 中國民航大學天津市智能信號與圖像處理重點實驗室, 天津 300300;2. 澳大利亞伍倫貢大學電氣計算機與通信工程學院, 澳大利亞 伍倫貢 999029)

摘要：提出了一種基于三次相位變換(cubic phase transform,CPT)和重構相位函數(reconstructing phase function,RPF)的空中高機動目標參數估計方法。為了實現目標高階參數的估計,該方法首先通過雙線性變換求得接收信號的相位函數,實現信號降階和待估參數的分離;然后利用多陣元采樣重構參考陣元的相位函數,等效增加了參考陣元相位函數的時間采樣,實現了參考相位函數的相干積累;最后進行參數估計。仿真結果表明,在輸入信噪比較低、采樣脈沖較少的情況下,該算法能夠以較高的精度實現對高機動目標的參數估計。

關鍵詞：高機動目標; 三次相位變換; 重構相位函數; 相干積累; 空時自適應處理

0引言

機載相控陣雷達以飛機為載體,機動性高、生存力強,相較地基雷達,其可視范圍遠,可擔任警戒、指揮等重要任務,在現代戰爭中的作用越來越重要[1]。當雷達處于下視狀態時,目標信號通常淹沒在雜波背景中[2],由于雜波信號功率遠大于目標信號功率,因而嚴重影響了雷達對目標信號的檢測。相比于單天線雷達,相控陣雷達通過多通道接收目標信號,在目標信號中引入了空間信息,通過空時二維濾波,能夠更加有效地抑制地雜波。空時自適應處理[3](space-time adaptive processing,STAP)技術經過幾十年的發展,已成為應用在該領域的關鍵性技術。隨著航空航天技術的不斷發展,空中來襲目標的機動性越來越高,此時用速度及加速度并不能準確描述目標運動狀態,需要引入更高階的運動參數—急動度[4-5]來實現對高機動目標的精確描述。和機動性較低的目標相比,高機動目標的回波非平穩,多普勒走動較為嚴重,傳統STAP的目標回波平穩的假設不再成立,使用傳統STAP技術處理高機動目標檢測問題性能不佳[3],因此對高機動目標檢測和參數估計方法的研究具有重要意義。

當目標做勻急動度運動時,目標回波信號具有三次相位信號(cubic phase signal,CPS)[6]形式。近年來,各種針對CPS信號的參數估計方法不斷出現,包括最大似然方法、離散多項式相位變換[7-9]、空間采樣重構時間采樣法、三次相位變換(cubic phase transform,CPT)[10-14]等。最大似然法理論效果最優,該方法采用搜索的方式對信號進行檢測,其運算復雜度隨著信號的階數劇烈上升,直接使用該方法解決三次相位信號問題,其運算復雜度將已立方為計,不利于實際系統的實現。離散多項式相位變換對信號進行四階非線性變換,實現了對三次相位信號參數的精確估計,但是該方法對采樣脈沖數和信噪比門限的要求較高[7]。CPT提出的應用背景是用于解決信號瞬時頻率變化率(instantaneous frequency rate,IFR)[6,15]的估計問題,該方法只對信號進行二階非線性變換,對采樣脈沖數和信噪比門限的要求較離散多項式相位變換方法低。但是受到機載預警雷達采樣脈沖數較少的限制,CPT方法仍然難以得到直接運用。空間采樣重構時間采樣法[16-18],能夠在采樣脈沖數較少的情況下提供較高的參數估計精度,但是由于該方法對三階信號重構運算量,將其直接運用到三階參數估計問題中運算量較大。本文提出了一種基于CPT和重構相位函數(reconstructing phase function,RPF)的高機動目標參數估計方法,該方法通過雙線性變換求得接收信號的相位函數矩陣,實現信號降階和待估參數的分離;然后利用空間采樣重構參考陣元的相位函數,實現相位函數的相干積累;最后以搜索方式估計高機動目標運動參數。本文將所提算法與CRB界及傳統方法進行了比較。結果證明,在輸入信噪比較低、采樣脈沖數較少的情況下,本文方法能夠較為準確的估計目標參數。

1信號模型和問題描述

本節介紹高機動目標回波模型。如圖1所示,設機載平臺沿航向方向放置均勻線陣,陣元數為N,相干處理脈沖數為K,陣元間距為d=0.5λ,其中λ為雷達發射脈沖的波長。

對于急動度不變的高機動目標,其在慢時間k時刻與雷達平臺的距離為目標在初始時刻與雷達平臺的距離Ro及由于目標運動產生的距離增量ΔR(k):

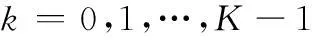
(1)

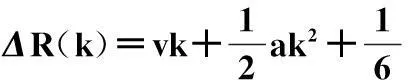
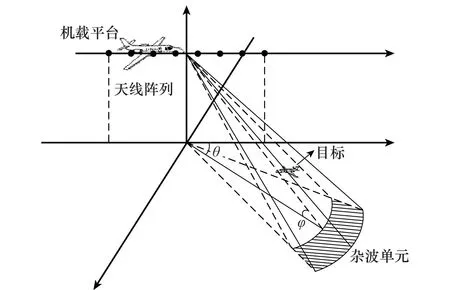
圖1　雷達與雜波散射單元幾何模型

在暫不考慮距離走動的情況下,對于第n(n=1,2,…,N)個陣元,在k時刻其接收的目標回波信號可以表示為

(2)

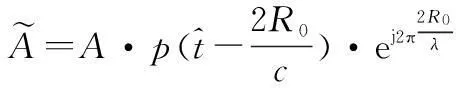
(3)

為了方便表示,令β1=4πv/λ、β2=2πa/λ、β3=2πja/3λ,則時間相位φtk可表示為

(4)

由式(3)可以看出:

(1) 對于雷達的接收信號,其空間相位φsn只與陣列結構(陣元數n及陣元間距d)及信號來向有關;

(2) 在目標運動參數一定的情況下,時間相位φtk僅由采樣時刻決定,與陣元結構(陣元數n及陣元間距d)無關,并且為采樣時刻k的三次函數。

由此可知,相控陣體制下,各陣元接收的勻急動度運動目標的回波信號為附帶了不同空間相位(不同陣元的空間相位不同)的三次相位信號。雷達接收的待檢測單元目標的回波可以表示為

(5)

則待檢測單元的空時快拍數據[3]為

(6)

式中,c和n分別表示雜波和噪聲。

2基于CPT和RPF的高機動目標參數估計方法

CPT最早應用在對信號的瞬時頻率變化率的估計問題上,經過發展成為一種有效的三次相位參數估計方法。它通過雙線性變換將三次相位信號轉化為信號的相位函數,實現對信號IRF的估計;然后通過估計兩個特定時刻的IRF,以解線性方程組的形式實現原三次相位信號的參數估計[6]。由于CPT方法實現三階參數估計需要較多的樣本,無法直接應用到機載相控陣預警雷達中。本文提出的基于CPT和重構相位函數的高機動目標參數估計方法首先對雜波抑制后的接收信號進行雙線性變換獲得信號的相位函數,實現信號降階和待估參數分離,然后通過重構相位函數,將多陣元短的相位函數重構成為參考陣元長的相位函數,實現相干積累,最后進行參數估計。

2.1雙線性變換

對于第n個陣元的接收信號srn(k),定義其瞬時頻率變化率為

(7)

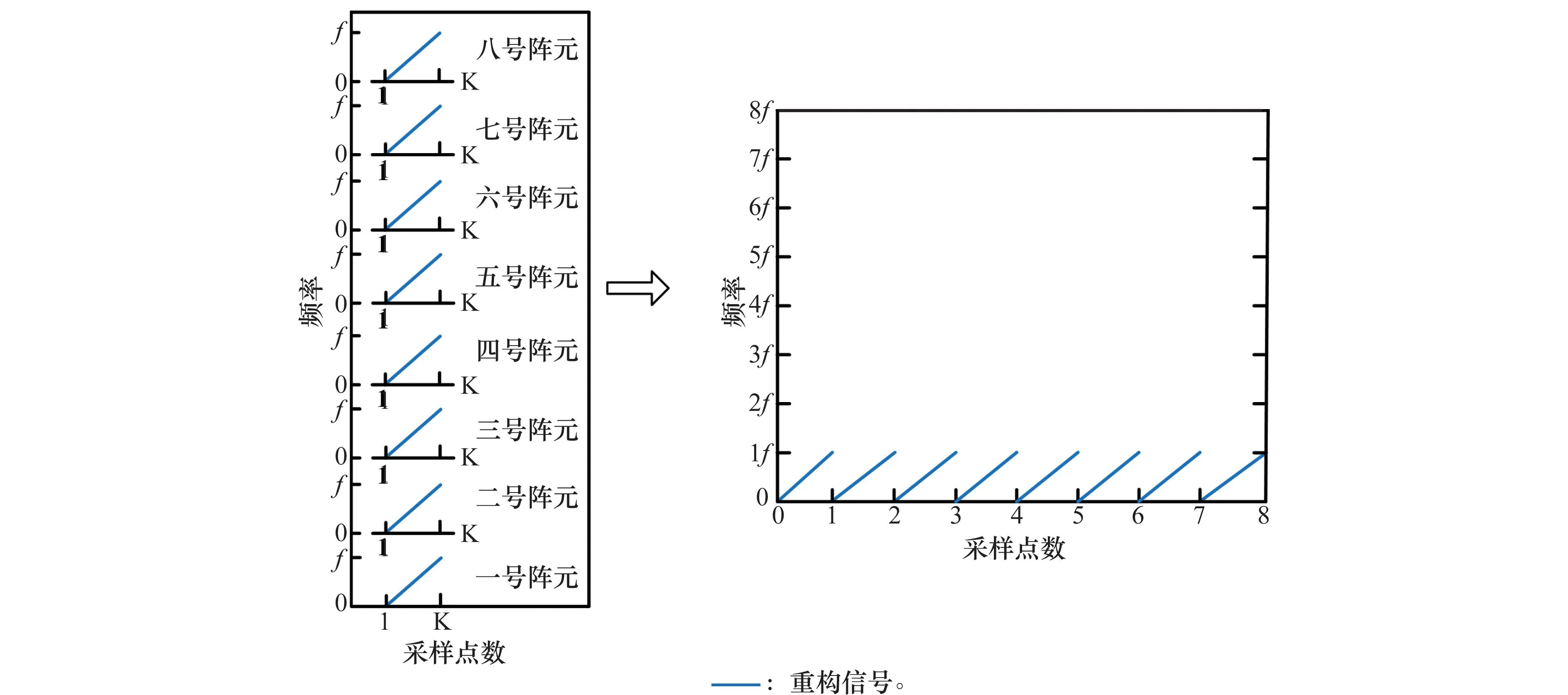
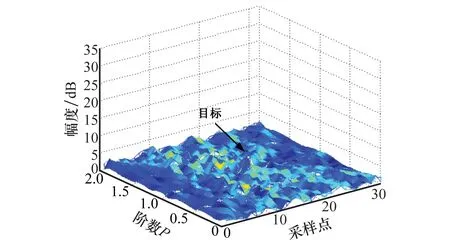
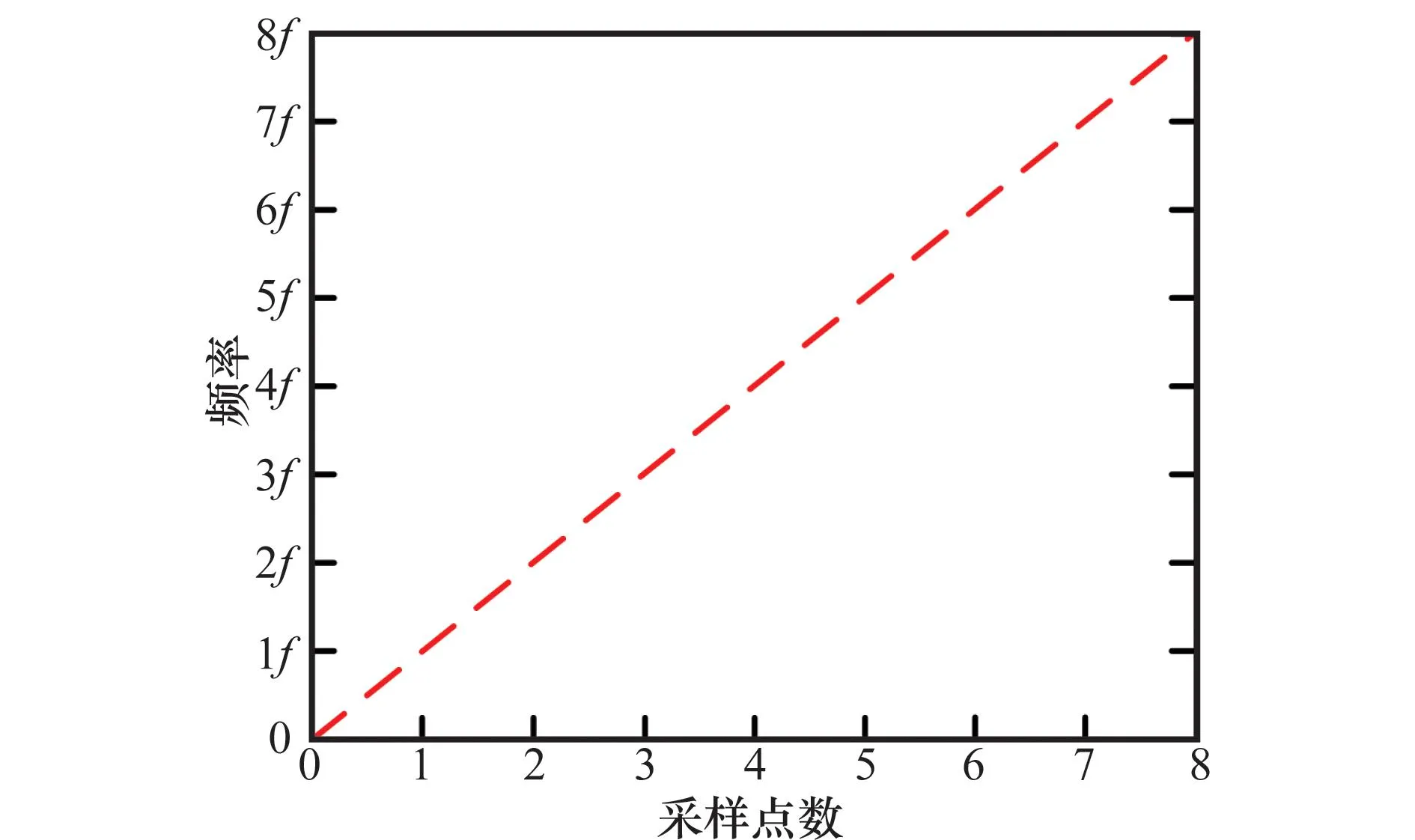
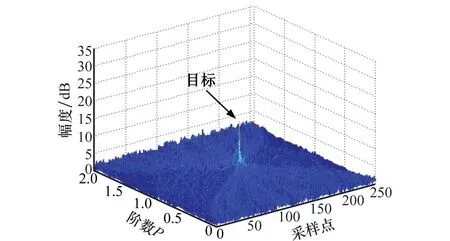
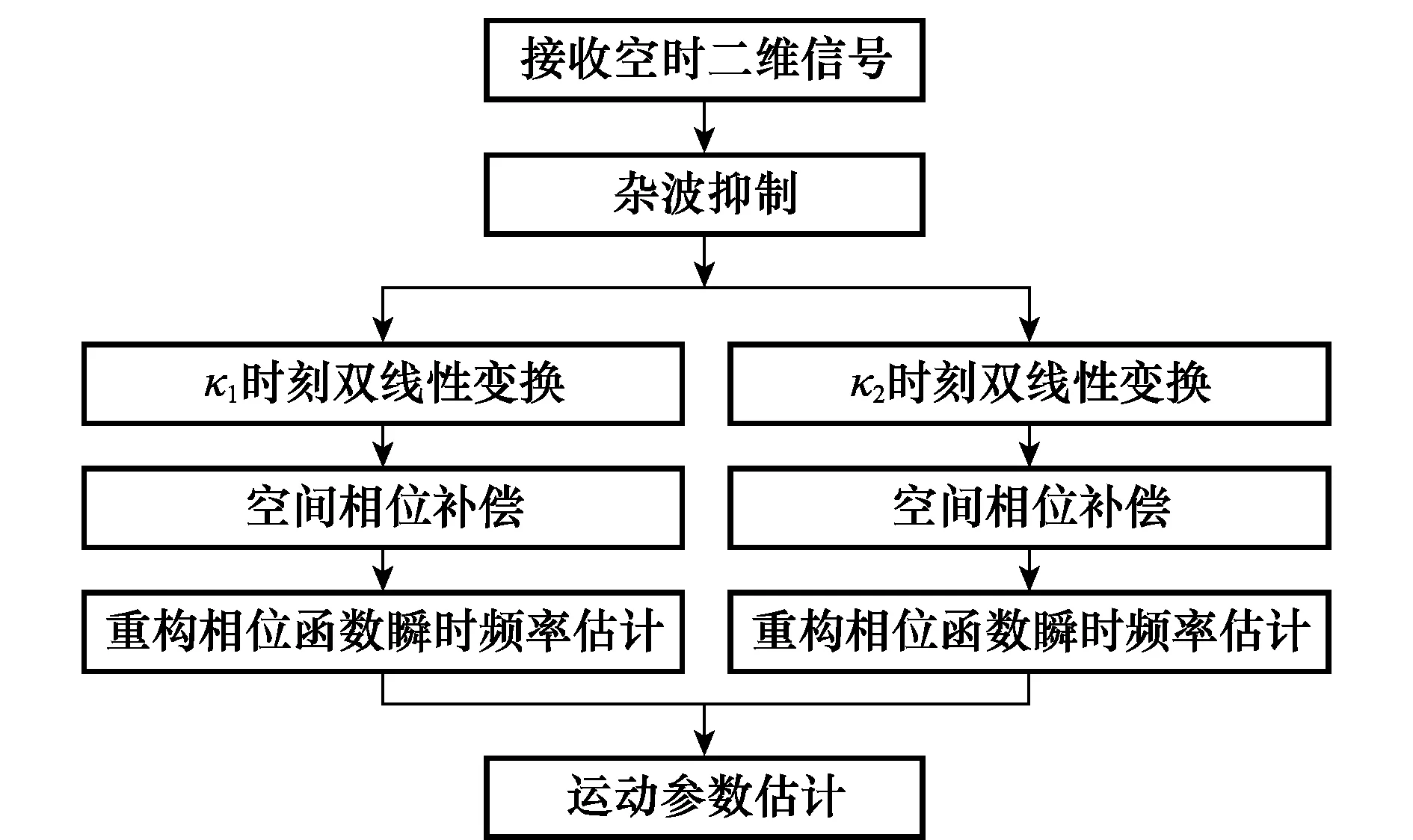
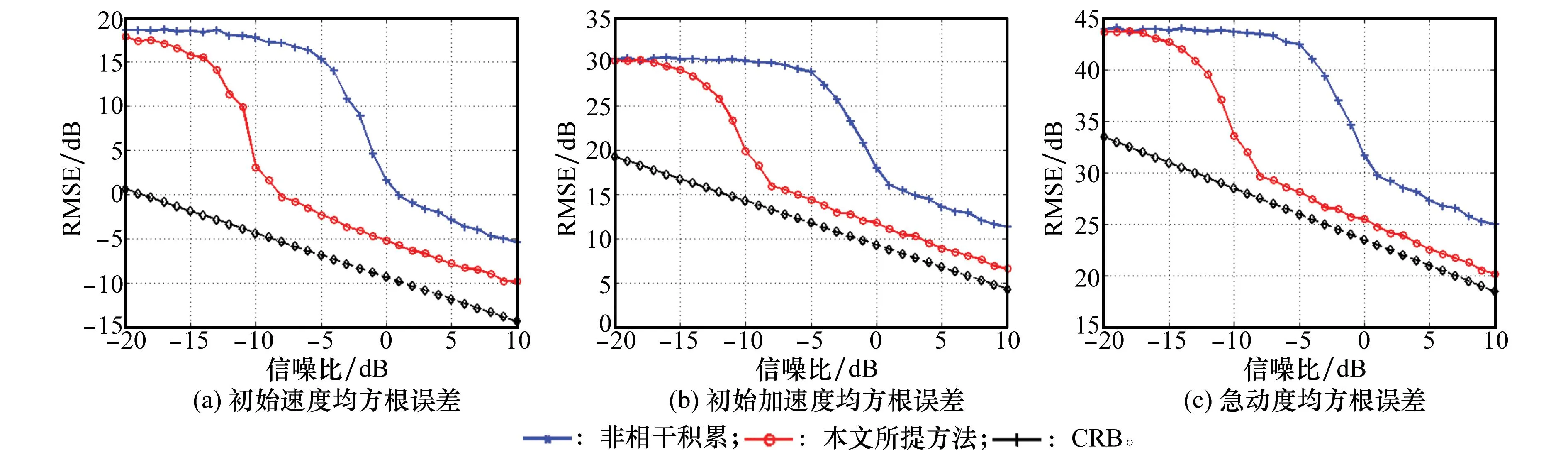
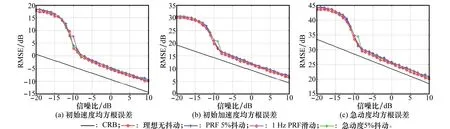
可以看出,瞬時頻率變化率是原信號二階、三階參數β2、β3的線性組合。本文通過在κ(0<κ

(8)

式中

(9)

(10)

(11)

由式(8)可以看出，pn κ(τ)為自變量為τ的二次相位信號。亦即經過雙線性變換,三次相位信號srn(k)被降階成二次相位信號pn κ(τ),其自變量為變換延遲τ,參數為瞬時頻率變化率Ωκ,而Ωκ只與β2、β3有關,與β1無關,因而實現了運動參數的分離。

在κ時刻,對每個陣元接收的目標信號srn(k)進行雙線性變換,得到κ時刻雷達接收的目標信號的相位函數矩陣D,其表達式為

(12)

式中

(13)

(14)

式中,pcn κ(n=1,…,N)是與空間相位無關的關于變換延遲τ的二次相位函數；Φs為空間相位對角矩陣。

2.2重構相位函數[16]

由式(12)可知,各陣元目標的相位函數pn κ(τ)具有二次相位信號形式,并且不同陣元之間的相位函數只相差一定的空間相位。由式(2)可知,運動參數引起的多普勒展寬僅體現在時間相位上,與空間相位無關,本文采用文獻[18]的方法對空間相位進行補償(本文以1號陣元為參考陣元進行補償),補償后的相位函數矩陣為

(15)

式中，Dc表示補償空間相位后的相位函數矩陣。由式(13)、式(15)可見,補償空間相位后,不同陣元間的相位函數相同,其時頻圖如圖2所示。可以看出,各陣元的相位函數的時頻圖相同,但由于不同陣元間相位不連續,無法直接進行相干積累。此時對每個陣元的相位函數分別進行分數階傅里葉變換(fractional Fourier transform,FrFT),再進行非相干積累,其效果如圖3所示(信噪比=0 dB)。可以看出,在脈沖數較少的情況下,非相干積累無法利用各陣元相位函數的相位信息,目標能量積累效果較差。

圖2　重構前8陣元接收信號相位函數時頻圖

圖3　重構前8陣元接收信號相位函數非相干積累圖

對單個陣元來說,其接收信號采樣脈沖數越多,采樣時間越長,其能量積累效果越好。基于此,重構相位函數法以某一陣元接收目標信號的相位函數為參考,補償其他各陣元目標相位函數的時間相位,然后進行拼接(即用空間采樣代替時間采樣),將多陣元采樣脈沖少、相位不連續的相位函數,重構成為參考陣元采樣脈沖多、相位連續的相位函數,使得多陣元接收信號相位函數能夠進行相干積累。重構的參考陣元的目標相位函數時頻圖、能量積累圖分別如圖4和圖5所示(信噪比=0dB)。由圖4、圖5可見,重構后的相位函數相位連續,因此能夠實現多陣元相位函數的相干積累,使得能量積累效果大大提升。

圖4　重構后8陣元接收信號相位函數時頻圖

圖5　重構后8陣元接收信號相位函數相干積累圖

為了討論方便,下面以兩陣元為例,討論如何重構接收信號的相位函數。設在κ時刻兩陣元接收信號的相位函數矩陣為Dc,其表達式為

(16)

式中

(17)

其中,pc1κ、pc2κ分別對應1號及2號陣元接收信號的相位函數。利用兩個陣元重構后的參考陣元相位函數[16]可表示為

(18)

式中,prcp表示重構所得相位函數；⊙為Hadamard積；Δφ2為重構時2號陣元所需補償的相位,可表示為

(19)

可以看出,補償pc2κ時間相位后再跟pc1κ拼接,等效為增加了pc1κ的時間采樣點數。當陣元數增加到N時,重構相位函數的表達式為

(20)

式中

(21)

2.3構造代價函數

上述方法在補償時間相位Δφn中,需要使用信號瞬時頻率變化率Ωκ作為重構參數。由式(10)可知,由于目標運動參數未知,Ωκ實際是未知的,這使得無法直接利用各陣元的相位函數進行重構。文獻[16]指出,當補償的瞬時頻率變化率為Ωκ,重構的相位函數積累能量最大。因此構造代價函數對Ω進行估計

(22)

式中,prcp(Ω)表示以Ω為重構參數對接收信號進行重構相位函數運算；ZFP[·]表示FrFT算子。

2.4運動參數估計

(23)

由式(23)可得

(24)

(25)

再由式(3)中參數轉換關系,求解高機動目標的運動參數估計值為

(26)

2.5算法流程

本文提出的基于CPT和RPF的空中高機動目標參數估計的方法流程如圖6所示。

圖6　本文方法實現框圖

步驟 1雜波抑制[21]。本文通過將待檢測的接收數據投影到由各距離單元接收信號訓練所得的雜波子空間的正交子空間中,實現雜波白化,得到雜波抑制后的回波數據。

步驟 2各陣元接收信號雙線性變換。選取兩個特定時刻κ1和κ2,按式(8)對接收數據進行雙線性變換,相位函數矩陣D1和D2。

3仿真分析

仿真參數設置:天線為正側視理想均勻線陣,陣元數N=8,陣元間距為半波長。載機速度120m/s,平臺高度10km,雷達工作波長0.32m/s,雷達快時間采樣頻率為2MHz,脈沖重復頻率1 500Hz,相干處理脈沖數K=128,輸入信噪比SNR=0dB,雜噪比CNR=50dB。高機動目標處于方位角60°處,初始速度20.1m/s,加速度99.1m/s2,急動度40.1m/s3,蒙特卡羅實驗次數為400次。

圖7為利用文中方法進行雜波抑制后的空時二維譜,可以看出,將接收信號向雜波子空間的正交子空間投影后,在原雜波處形成了較深的凹口,使得雜波得到了有效的抑制。但同時可以看出,由于目標機動性高,其多普勒展寬較為嚴重。

圖7　雜波抑制后的功率譜

圖9為不同方法得到的各階參數估計值的均方根誤差與CRB界隨信噪比變化的曲線圖。藍色星形線表示傳統CPT方法非相干積累方法的估計性能曲線,紅色圓圈線表示本文方法的估計性能曲線。從仿真結果可知,本文方法能夠更加精確的實現對目標參數的估計。

上述討論建立在目標運動參數恒定、雷達工作狀態理想穩定的情況下的。實際情況中,由于各種因素,并不能保證目標運動參數以及雷達工作參數完全穩定。其具體表現為目標運動中參數存在抖動起伏、雷達PRF存在抖動、雷達PRF存在滑變等情況。為了進一步說明所提算法的性能,本文對上述幾種情況進行了仿真驗證,其結果圖如圖10所示。

圖8　補償急動度、加速度后的信號頻譜

圖9　目標參數均方根誤差隨信噪比變化曲線

圖10　目標參數均方根誤差隨信噪比變化曲線

圖10中,星型線表示目標急動度在真值附近有5%隨機起伏情況下,所提算法估計得到的目標參數均方根誤差隨信噪比變化曲線圖。可以看出,目標急動度隨機起伏對所提算法估計結果影響較小。

十字線為雷達PRF存在10 Hz隨機抖動時,目標參數均方根誤差隨信噪比變化曲線圖,可以看出,當脈沖重復頻率存在10 Hz隨機抖動時(實際情況中,現代雷達的頻率穩定度在10-5量級左右,在文本仿真參數設置中,選擇的10 Hz抖動量所占量級約為10-3左右,屬于抖動量較大、較為惡劣的情況),所提算法依然能夠較精確地實現機動目標參數估計。

菱形線為當雷達PRF存在+1Hz滑動時,目標參數均方根誤差隨信噪比變化曲線圖,可以看出當脈沖重復頻率存在的滑動量為+1 Hz時(實際情況中,現代雷達的頻率穩定度在10-5量級左右,本文仿真參數中,1 Hz的頻率滑動所占量級約為10-3,并且隨著采樣脈沖數的逐漸增加,其累積滑動量增加無法消除,屬于滑動量較大、較為惡劣的情況,屬于滑動量較大、較為惡劣的情況),所提算法的參數估計精度受到的影響較小。

4結論

(1) 本文主要研究了高機動目標的參數估計問題,所提方法利用CPT方法思想,實現信號的參數分離,因此能夠以較低的運算量實現高機動目標的運動參數估計。

(2) 所提方法由于采用了重構相位函數技術,以空間采樣代替時間采樣,因而能在一個CPI內雷達發射脈沖有限的情況下,獲得較為精確的參數估計結果。

(3) 通過仿真實現并與CRB界及傳統方法估計性能進行了比較,可以看出,所提方法能更好的逼近CRB界,在低信噪比下優勢更加明顯。

參考文獻：

[1] Zhang W. Analysis on airborne MIMO radar space time signal processing.[D]. Chengdu: University of Electronic Science and Technology of China, 2013. (張偉. 機載MIMO雷達空時信號處理研究[D]. 成都: 電子科技大學, 2013.)

[2] Klemm R.Principleofspace-timeadaptiveprocessing[M]. 3rd ed.UK：IET Publishers, 2006:1-133.

[3] Wang Y L, Peng Y N.Space-timeadaptiveprocessing[M].Beijing: Tsinghua University Press, 2000:1-57. (王永良,彭應寧. 空時自適應信號處理[M]. 北京:清華大學出版社,2000:1-57.)

[4] Wang Y, Li Q, Wang J. Research on maneuvering model algorithm based on vehicle tracking[C]∥Proc.oftheIEEEWorkshoponElectronics,ComputerandApplications, 2014: 585-588.

[5] Li X, Cui G, Kong L. High speed maneuvering target detection based on joint keystone transform and CP function[C]∥Proc.oftheRadarConference,2014:436-440.

[6] O’Shea P. A fast algorithm for estimating the parameters of a quadratic FM signal[J].IEEETrans.onSignalProcessing, 2004, 52(2): 385-393.

[7] Shimon P, Benjamin F. Discrete polynomial phase transform[J].IEEETrans.onSignalProcessing, 1995, 43(8): 1910-1914.

[8] Wu Y T, Hing C S, Liu H Q. Sub-based algorithm for parameter estimation of ploynomial phase signals[J].IEEETrans.onSignalProcessing, 2008, 56(10): 4977-4983.

[9] Shimon P. Estimation and detection with the discrete polynomial phase transform[D]. Davis:University of California,1993.

[10] O’Shea P. A new technique for estimating instantaneous frequency rate[J].IEEESignalProcessingLetters, 2002, 9(2): 251-252.

[11] You W, He Z S, Hu J F. et al. A movement compensation algorithm for maneuvering target in skywave radar[J].ModernRadar,2013,35(11):26-29.(游偉,何子述,胡進峰,等.一種天波雷達機動目標運動補償算法[J].現代雷達,2013, 35(11): 26-29.)

[12] Zheng J, Su T, Liu Q H, et al. Fast parameter estimation algorithm for cubic phase signal based on quantifying effects of Doppler frequency shift[J].ProgressinElectromagneticsResearch, 2013, 142(5): 57-74.

[13] Wang P, Yang J Y. Parameter estimation of multicomponent quadratic FM signals using computationally efficient Randon-CPF[C]∥Proc.oftheEuropeanSignalProcessingConference,2006:4-8.

[14] McKilliam R, Pollok A. On the Cramer-Rao bound for polynomial phasesignals[J].SignalProcessing,2014,95(1):27-31.

[15] Orovic I, Stankovic S, Thayaparan T. Time-frequency-based instantaneous frequency estimation of sparse signals from incomplete set of samples[J].SignalProcessing, 2014, 8(3): 239-245.

[16] Wu R B, Wang X H, Li H, et al. Detection and parameter estimation of air maneuvering targets via reconstructing time samples[J].JournalofElectronics&InformationTechnology,2012, 34(4): 936-942. (吳仁彪,王小寒,李海,等.基于重構時間采樣的空中機動目標檢測與參數估計[J].電子與信息學報,2012,34(4):936-942.)

[17] Li H, Wang X H, Wu R B. Detection and parameter estimation of multicomponent air maneuvering targets via RELAX[J].AeronauticaetAstronauticaSinica, 2013, 34(4): 873-881. (李海,王小寒,吳仁彪. 基于RELAX的空中多機動目標檢測與參數估計[J]. 航空學報, 2013, 34(4): 873-881.)

[18] Zhou F.Study of motion compensation, narrow band interference suppression and single channel GMIT of airborne SAR[D]. Xi’an: Xidian University, 2007.(周峰. 機載SAR運動補償和窄帶干擾抑制及其單通道GMTI的研究[D].西安:西安電子科技大學,2007.)

[19] Zhang X H. Detection and parameter estimation of polynomial phase signal[D]. Chengdu: University of electronic science and technology of China, 2011.(張希會.多項式相位信號的檢測與參數估計[D]. 成都: 電子科技大學, 2011.)

[20] Pham D S, Zoubir A M. Analysis of multicomponent polynomial phase signals[J].IEEETrans.onSignalProcessing, 2007, 55(1): 56-64

[21] Wu R B, Jia Q Q, Li H. Detection of fast moving dim targets on airborne radar via STAP[J].JournalofElectronics&InformationTechnology,2011, 33(6): 1459-1464. (吳仁彪, 賈瓊瓊, 李海.機載雷達高速空中微弱動目標檢測新方法[J]. 電子與信息學報, 2011, 33(6):1459-1464.)

李海(1976-),男,副教授,博士,主要研究方向為機載氣象雷達信號處理、自適應信號處理、動目標檢測、干涉合成孔徑雷達信號處理。

E-mail:haili@cauc.edu.cn

周盟(1988-),男,碩士研究生,主要研究方向為空時自適應信號處理、動目標檢測。

E-mail:bard_belief@hotmail.com

吳仁彪(1966-),男,教授,博士后,主要研究方向為自適應陣列信號處理、空時自適應處理、探地雷達信號處理。

E-mail:rbwu@vip.163.com

Detection and parameter estimation of air highly maneuvering targets via CPT and RPF

LI Hai1,2, ZHOU Meng1, WU Ren-biao1

(1.TianjinKeyLabforAdvancedSignalProcessing,CivilAviationUniversityofChina,Tianjin300300,China; 2.SchoolofElectrical,ComputerandTelecommunicationsEngineering,UniversityofWollongong,Wollongong999029)

Abstract:For the detection and parameter estimation of the air highly maneuvering targets, a new algorithm is proposed, which combines the cubic phase transform (CPT) with the reconstructing phase function (RPF). First, the bilinear transform is used to obtain the phase function matrix of the array signal,which leds to the signal reduction and estimated parameters segregation. Then, by compensating the spatial phase of the phase function matrix based on the array manifold and reconstructing the phase function based on the time phase relevance of the phase function of each array signal, a phase continuous phase function which is rich in sampling pulses is obtained. The proposed method is equivalent to increasing coherent accumulative time of the signal. In the condition of low signal-to-noise and few sampling pulses, this method can achieve good parameter estimation results. Numerical examples are provided to demonstrate the performance of the proposed algorithm.

Keywords:highly maneuvering targets; cubic phase transform; reconstructing phase function; coherent integration; space time adaptive processing (STAP)

收稿日期：2015-06-19；修回日期：2015-11-16；網絡優先出版日期：2016-01-07。

基金項目：國家自然科學基金 (61471365, 61571442, 61231017)；中央高校基本科研業務費專項資金(3122015B002,Y15-12);中國民航大學藍天青年學者培養經費資助課題

中圖分類號：TN 957.51

文獻標志碼：A

DOI:10.3969/j.issn.1001-506X.2016.06.03

作者簡介：

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160107.0919.002.html