擴展卡爾曼濾波器的目標機動信息估計研究

曹有亮，張金鵬

(中國空空導彈研究院，河南 洛陽　471009)

?

擴展卡爾曼濾波器的目標機動信息估計研究

曹有亮，張金鵬

(中國空空導彈研究院，河南 洛陽471009)

摘 要:針對目標機動信息估計時的狀態方程非線性及目標機動頻率未知的特點,對三維線性卡爾曼濾波器的狀態量進行了擴維。利用擴展卡爾曼濾波器(EKF)完成了目標機動信息估計算法設計,并通過仿真驗證了不同條件下濾波器對目標機動頻率、機動加速度及加加速度的估計特性。同時,對濾波器估值誤差的收斂性進行了仿真評估,驗證了算法的有效性。

關鍵詞:擴展卡爾曼濾波器;目標機動估計;非線性狀態方程

0引言

在末制導過程中，對于非機動目標，采用比例制導律可以達到滿意的制導精度, 而且在一定的線性化簡化條件下，可以證明比例制導律的最優性。但是目標的機動會嚴重影響比例導引的性能，導致脫靶量增大。為了改善制導回路的性能，減小脫靶量，需要在制導律設計中對目標機動加速度進行補償，如在比例制導律基礎上增加目標機動補償項而得到擴展比例制導律，此時目標機動信息的準確性將對制導性能產生較大影響。

對于目標機動信息的估計問題，廣泛采用卡爾曼濾波方法進行處理，在研究中一般需要假設目標的機動模型及隨機機動的統計特性。本文假設導彈采用雷達導引頭, 可以提供視線角和相對距離、彈目接近速度信息作為系統的輸出，針對尋的末制導中狀態方程與觀測方程非線性以及目標機動頻率未知的特點，利用擴展卡爾曼濾波器(EKF)設計目標機動信息估計算法，對目標機動頻率、機動加速度及加加速度估計的準確性進行仿真，驗證濾波器誤差的收斂性。

1擴展卡爾曼濾波算法(EKF)

若系統狀態方程與觀測方程為非線性形式，則可采用擴展卡爾曼濾波器，其處理步驟為

(1)

(2)

(3)

為了減小線性化誤差，提高濾波跟蹤精度，可將非線性方程的泰勒級數截斷至二階項，得到二階擴展卡爾曼濾波器，其濾波過程如下：

(4)

(5)

(6)

擴展卡爾曼濾波在目標狀態預測值處對非線性觀測進行線性近似，若能在更加精確的狀態估計值處做近似，可以預知線性化誤差更小，濾波估計精度更高，因此在狀態估計值處線性化對狀態進行再次更新，這種處理可以一直迭代下去，稱為迭代卡爾曼濾波。其處理步驟為

(7)

2基于EKF的目標機動信息估計

假設目標的機動形式為正弦機動，實際上無論是逃逸機動還是蛇形機動，在慣性系中都可以認為是一種正弦機動，所以此假設具有一定的合理性。目標正弦機動的尋的回路模型見圖1。

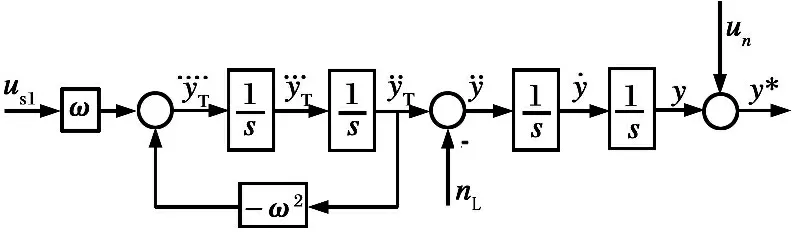
圖1正弦機動的尋的回路模型

也可用狀態空間方程來描述上述系統：

(8)

式中： us1和us2為過程噪聲。過程噪聲us1的功率譜密度如下：

式中： ωEXP為目標最大可能的機動頻率； nTMAX為目標最大機動值； tF為整個飛行時間。us2的功率譜密度Φs2則需要通過系統試驗來獲得。

由于引入目標機動頻率為狀態量，系統狀態方程將為非線性。以此為基礎的濾波器也將為非線性擴展卡爾曼濾波器，而不是線性卡爾曼濾波器。但此模型的測量方程仍然為線性的，如下所示：

(9)

系統動態特性矩陣可以通過對系統狀態方程求偏導得到：

(10)

根據系統狀態方程，可計算得到系統動態特性矩陣：

(11)

可以使用一個二階泰勒展開式來得到近似的基本矩陣：

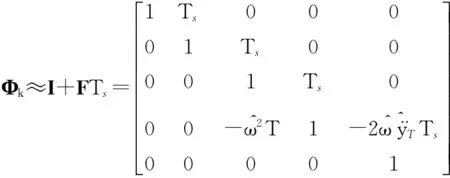
(12)

根據狀態方程，可得連續過程噪聲矩陣：

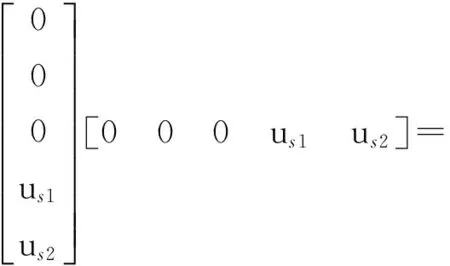
(13)

式中： 頻譜密度Φs1和Φs2之前已經定義。離散過程噪聲矩陣可以依據下式通過連續過程噪聲矩陣得到：

(14)

將連續過程噪聲矩陣和基本矩陣代入式(14)，可得離散過程噪聲矩陣：

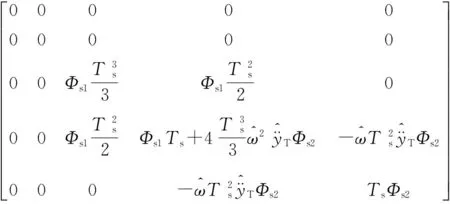
(15)

當濾波器工作時，卡爾曼增益是從Ricatti矩陣方程式計算得到。Ricatti矩陣方程是一系列遞歸矩陣方程式，如下：

(16)

式中：Pk為協方差矩陣，代表更新前的狀態估值誤差； Mk也為協方差矩陣，代表更新后的狀態估值誤差。

在得到卡爾曼增益矩陣Kk后，擴展卡爾曼濾波器的狀態估計方程為

(17)

3仿真驗證

為了啟動Ricatti方程式，需要初始方差矩陣，該矩陣表示估值中的初始不確定值。為初始方差矩陣選擇適當的值是濾波器設計的一項關鍵技術。本文的仿真中，利用真值對初始方差矩陣進行初始化，工程上可對目標傳感器的精度進行測試和評估，然后設計合理的方差矩陣。

為了驗證濾波算法的有效性，引入一個幅值為3g且機動頻率ω為2rad/s的目標正弦機動，利用EKF濾波遞推算法對其進行估計。在測角方差為1mr，頻譜密度Φs2為0且機動頻率初始值為-1rad/s的情況下，仿真結果如圖2～4所示。

從圖2～4可以看出，機動頻率初始值為-1rad/s的情況下，目標機動頻率估值在穩態為-2.5rad/s左右，模值基本接近真值。在測角方差為1mr的情況下，加速度和加加速度的估值在大部分情況下嚴重偏離真值，只是在飛行時間末端收斂在真值附近。將測角方差降低至0.1mr且機動頻率初始值為1rad/s，仿真結果如圖5～9所示。

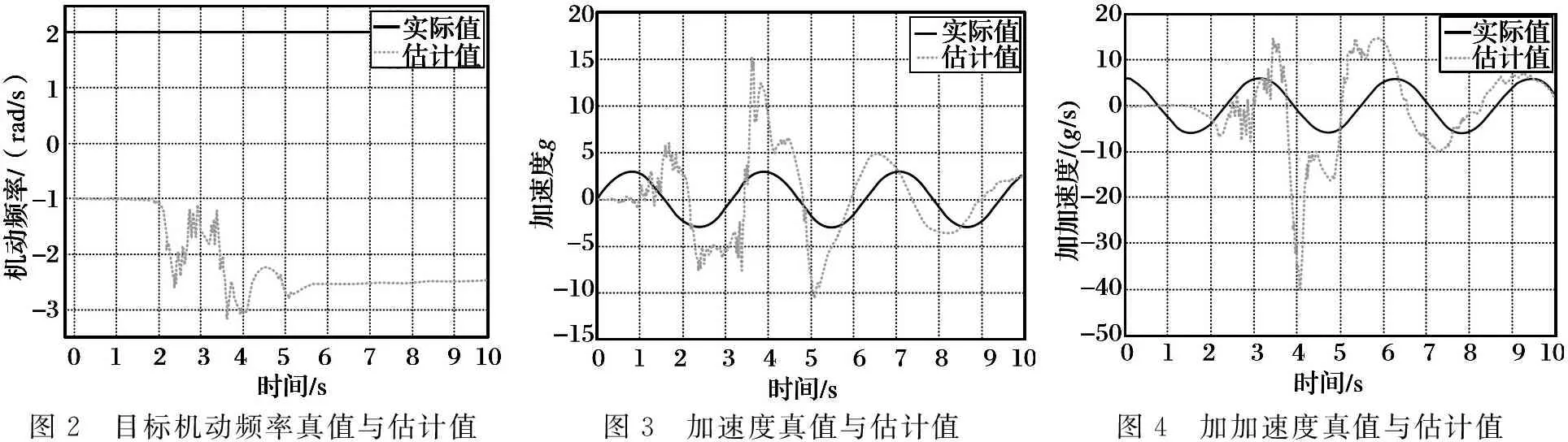
圖2 目標機動頻率真值與估計值圖3 加速度真值與估計值圖4 加加速度真值與估計值

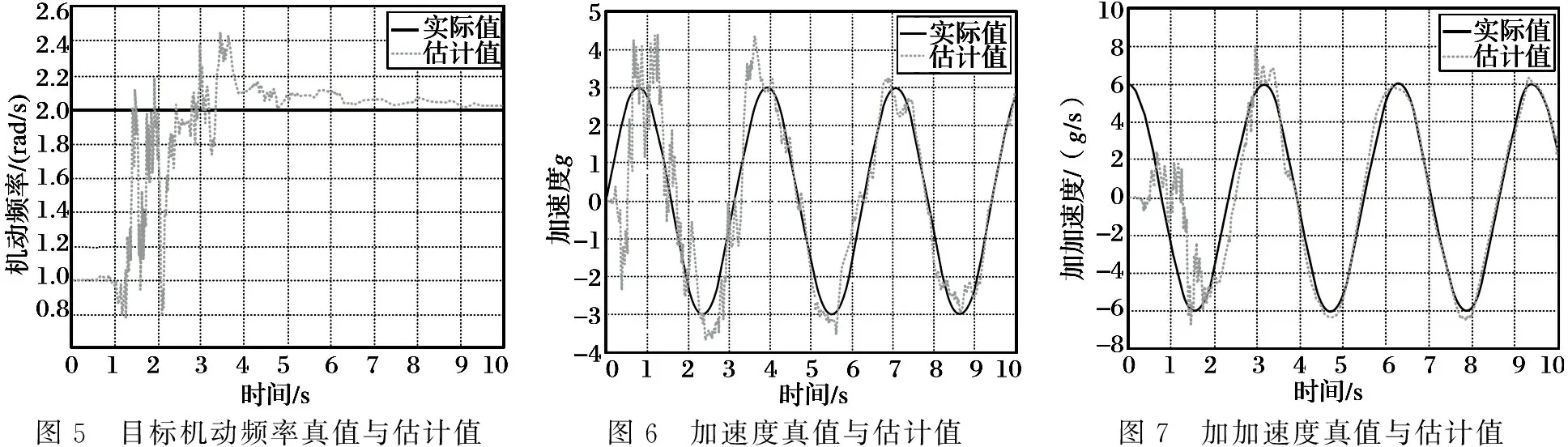
圖5 目標機動頻率真值與估計值圖6 加速度真值與估計值圖7 加加速度真值與估計值

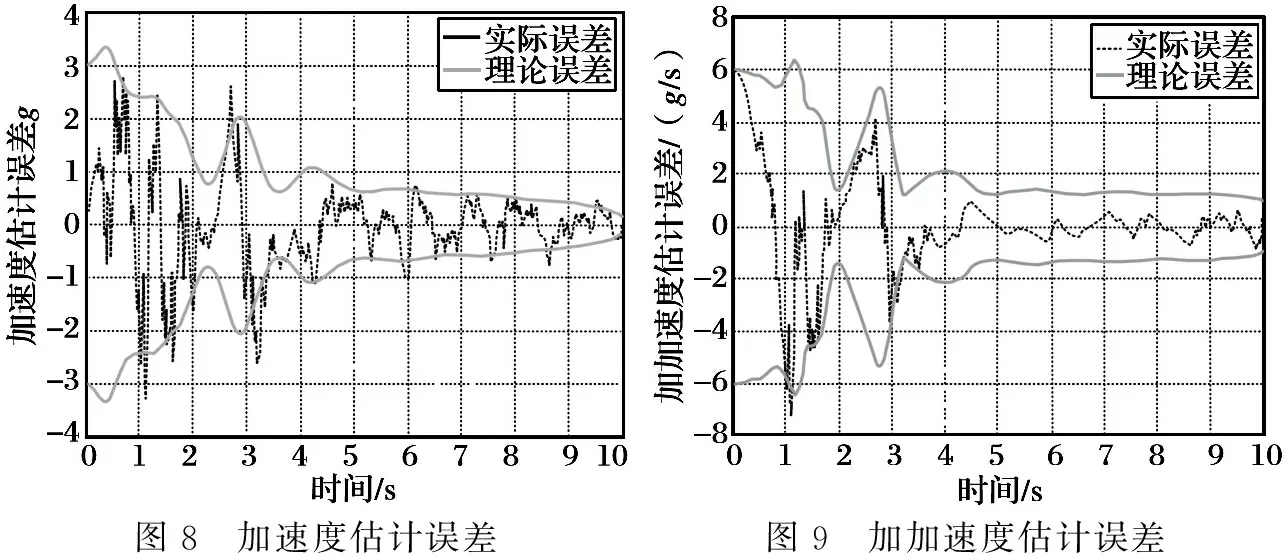
圖8 加速度估計誤差圖9 加加速度估計誤差

從圖5～9的仿真結果可看出，在降低測量噪聲及機動頻率初值誤差較小的情況下，加速度和加加速度在大部分飛行時間內都得到準確的估計，機動頻率也很快收斂到真值附近，估值誤差與理論值較相符。

4結論

本文針對目標機動信息估計時狀態方程非線性及目標機動頻率未知的特點，利用擴展卡爾曼濾波器(EKF)完成了目標機動信息濾波算法的設計。仿真驗證表明在較小測角噪聲下濾波器對目標機動頻率、機動加速度及加加速度具有良好的估計準確性，可以為制導系統及制導律提供更良好準確的目標機動信息，改善制導系統精度。

參考文獻：

[1] 馬克茂，賀風華，姚郁.目標機動加速度的估計與導引律實現[J]. 宇航學報, 2009, 30(6): 2213-2219.

[2] 范紅旗, 樊建鵬, 付強. 機動目標運動建模技術綜述[C]∥ 國防科大電子科學與工程學院2011年會論文集, 2012.

[3]ZarchanP.TacticalandStrategicMissileGuidance[M].AIAA，1997.

[4] 安相宇，董朝陽，王青. 一種基于EKF技術的天線罩瞄準誤差補償方法[J]. 系統仿真學報, 2007, 20(15):4099-4103.

[5]BrysonAE,HoYC.AppliedOptimalControl[M].NewYork:Blaisdell, 1969.

[6] 周荻.尋的導彈新型導引規律[M].北京：國防工業出版社，2002.

[7] 黃曉雷，牛申閣. 擴展卡爾曼濾波在無人機航跡控制系統中的應用研究[J]. 航空兵器，2008(2)：11-13.

[8] 沈亮，萬平，耿源. 雷達導引頭自適應卡爾曼濾波算法研究[J]. 航空兵器，1994(2)：30-37.

[9] 葛泉波，李文斌，孫若愚，等. 基于EKF的集中式融合估計研究[J]. 自動化學報，2013，39(16)：816-825.

Researeh on Target Maneuvering Information Estimation Method of EKF

Cao Youliang, Zhang Jingpeng

(China Airborne Missile Academy，Luoyang 471009，China)

Abstract:For the characteristics of the nonlinear state equation and the unknown target maneuvering frequency on target maneuvering information estimation, the state of three-dimensional linear Kalman filter is extended. The extended Kalman filter is used to design target maneuvering information estimation algorithm, and by simulation the estimate characteristics of target maneuveing frequency, acceleration and jerk under different conditions are verified. The convergence of the estimation error is simulated and evaluated, and the effectiveness of the algorithm is verified.

Key words:EKF; target maneuver estimation; nonlinear state equation

DOI：10.19297/j.cnki.41-1228/tj.2016.01.007

收稿日期：2015-06-09

基金項目：航空科學基金項目(20110112001)

作者簡介：曹有亮(1984-)，男，河南焦作人，碩士，工程師，研究方向為制導與控制技術。

中圖分類號:TJ765

文獻標識碼:A

文章編號:1673-5048(2016)01-0040-05