風電機組關鍵部件維修優化

文 | 翟長武，董玉亮

?

風電機組關鍵部件維修優化

文 | 翟長武，董玉亮

風電機組的高可靠性是風力發電的根本要求，然而潮濕、腐蝕、風沙、震動、極寒、極熱等惡劣運行環境，不完善的運行控制策略和設計安裝缺陷導致風力發電裝置總體可靠性較低。較低的可靠性導致風電場運行與維護費用居高不下，據統計陸上風電場運行與維護費用占發電總成本的10％－20％。降低運行與維修費用主要有兩個途徑：一方面是應用狀態監測技術進行故障的早期探測，減少事后維修；另一方面采用維修優化技術，獲得最優的維護策略，降低維修費用。因此，開展風電機組關鍵部件維修策略優化研究，根據獲得的最優策略合理安排維修，對提高風電機組運行安全性和可靠性，降低運行與維護費用具有重要的意義。

風電機組關鍵部件故障分析

典型的齒輪驅動風電機組結構如圖1所示。

表1給出了齒輪驅動風電機組各系統故障率統計數據。可以看出，電氣系統、變槳系統、風輪系統、傳動系統、發電機系統、主控系統、監測系統、制動系統具有較高的故障率；而其中齒輪箱、發電機、風輪、主軸和主軸承的維修費用和停機損失遠遠高于其它部件。本文將齒輪箱、發電機、主軸和主軸軸承作為風電機組關鍵部件，對其維修策略進行優化。

關鍵部件主要故障模式和監測方法如表2所示。

風電機組關鍵部件維修策略優化模型

一、風電機組可靠性分析

風電機組可靠性分析流程如圖2所示。

（一）可靠性數據收集

針對某一風電場的同類型風電機組，收集風電機組各關鍵部件的失效時間、失效前工作時間和失效原因，并按失效時間的先后順序列表，作為可靠性統計分析時參數估計的數據。

（二）可靠性數據統計分析

目前在可靠性建模中應用比較廣泛的模型有指數分布、正態分布、伽馬分布、對數正態分布、威布爾分布和極值分布。本文采用極大似然估計的方法，擬合風電場設備的故障數據曲線，得到設備的故障率分布函數以及可靠度函數。下面以兩參數威布爾分布函數為例，給出參數估計方法。

兩參數威布爾分布概率密度為：

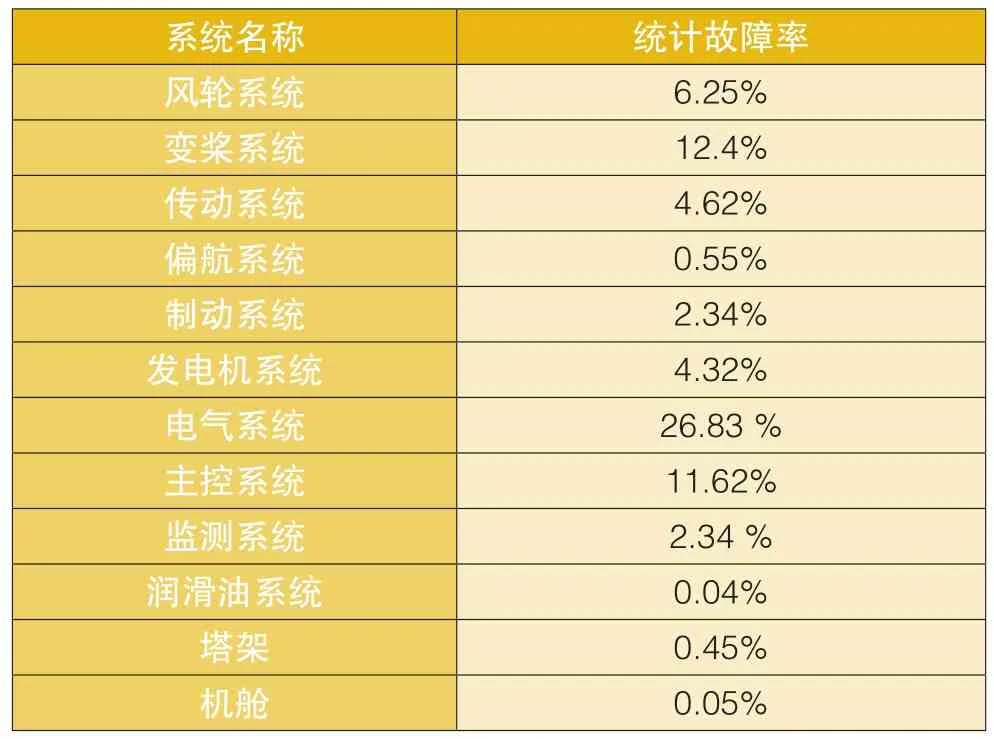
表1 風電機組各系統故障率統計表

故障率函數：

對于容量為n的完全樣本數據x1≤x2≤…≤xm，取威布爾分布的對數似然函數：

根據式（4）式取得極大值時的β，γ的估計值，即可得到故障率的兩參數威布爾分布。

（三）部件/系統可靠性計算

獲得β，γ的估計值后便可用式（5）計算部件可靠度

利用建立的系統可靠性框圖，便可計算系統不同工作時間的可靠度。

二、維修費用模型

風電機組進行以最小維修費用為目標的維修任務決策及優化，首先應建立維修/故障費用模型。一般地，維修/故障費用可分為預防維修費用、維修費用和故障維修費用。

（一）預防維修費用

預防維修費用指設備按照計劃進行維修發生的維修費用，包括計劃停運損失費用和預防維修材料、起重設備、人工費用。一次預防維修費用可表示為：

式中：Cploss－ 一次預防維修停運損失；Cpre－ 一次預防維修材料、起重設備及人工費用。

（二）機會維修費用

機會維修費用指設備進行機會維修（設備在非計劃情況下維修，此時尚未出現功能故障）發生的維修費用，包括非計劃停運損失費用和非計劃維修材料、起重設備及人工費用。一次機會維修費用可表示為：

式中：Coloss－ 一次機會維修停運損失；Core－一次機會維修材料、起重設備、人工費用。

（三）故障維修費用

故障維修費用指設備進行故障維修發生的費用，包括故障停運損失費用和故障維修材料、起重設備及人工費用。一次故障維修費用表示為：

式中：Cfloss－故障維修停運損失；Cfre－故障維修材料、起重設備、人工費用。

通用的停運損失費用可以按式（9）計算：

式中：T－機組停運時間，包括部件購買運輸時間、修理/更換時間；W－機組額定功率（kW）； f－功率因子；Cenergy－上網電價。

通用的維修費用：

式中：Cmaterial－材料費用；Ctrans－運輸費用；Ccrane－起重機使用費用。

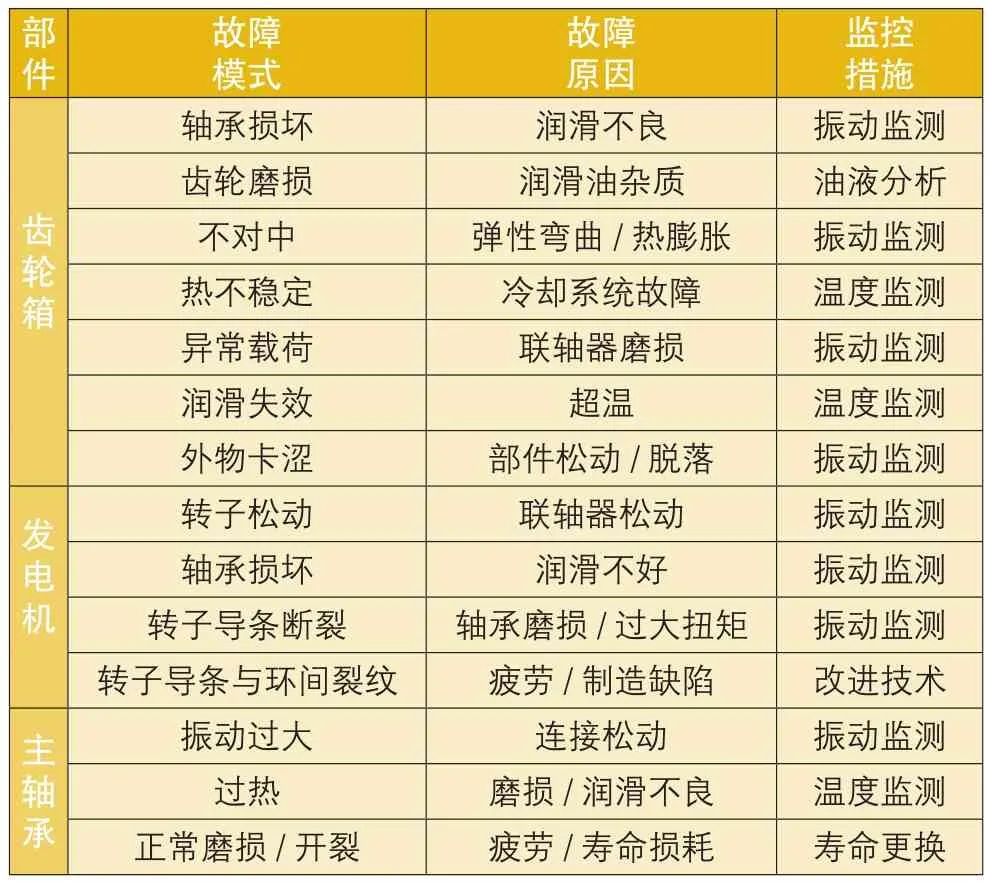
表2 風電機組關鍵部件故障模式分析

三、基于役齡的定期更換模型

定齡更換策略指設備或部件達到規定的使用間隔期（年齡）T，即使無故障發生也要進行預防性更換；如未到規定的使用間隔期T發生了故障，則對設備、部件作故障后更換。該策略適合于價格比較昂貴的設備及部件。

在已知部件的故障分布函數F（t）、一次故障維修費用Cf和一次預防維修費用Cp的條件下，可建立更換周期T內以單位工作時間維修/故障費用最小為目標的維修優化模型。

式中：Tj為可能的定期更換周期。

最優更換間隔可通過數值方法求解，給出一系列定期更換間隔Ti，帶入式（11）得到對應的單位時間期望平均費用C(Ti），畫出單位時間期望平均維修/故障費用隨定期更換間隔變化而變化的曲線，便可得到最優的定期更換間隔。

為與風電場現行維修策略相比較，這里給出該類設備事后更換策略的單位時間平均維修/故障費用。設風電場現行定期更換周期為k年，則單位時間期望平均維修/故障費用可由式（12）得到：

當采用事后更換策略時，則設備/部件在（0,t）時間內的失效次數可用更新函數H（t）來確定。更新函數定義為在（0,t）時間內失效（更新）次數[N（t）]的數學期望。

對于事后更換，單位時間內期望平均維修/故障費用為：

可以證明，當t→∞時，有下式成立：

因此，單位時間內期望平均維修/故障費用可由式（16）計算：

式中：MTBF為設備平均無故障工作時間。

算例分析

以某風電場為例進行算例分析。該風電場由26臺600kW風電機組組成。利用SCADA中故障歷史數據，統計分析得到其關鍵部件的可靠性威布爾分布參數如表3所示。

風電機組故障/維修費用統計值如表4所示。

對各關鍵部件利用式（11），獲得其單位時間平均維修/故障費用曲線，如圖3－圖8所示。

從圖3－圖8可以看出， 主軸和主軸承沒有最優更換間隔期，而齒輪箱齒輪、高速軸軸承、中速軸軸承、中速軸軸承和發電機軸承具有最優更換間隔期。表5列出了各部件分別采用最優間隔更換策略和故障更換策略的平均維修/故障費用。可以看出齒輪箱和發電機關鍵部件采用優化的定期更換策略可以大大降低平均維修/故障費用。

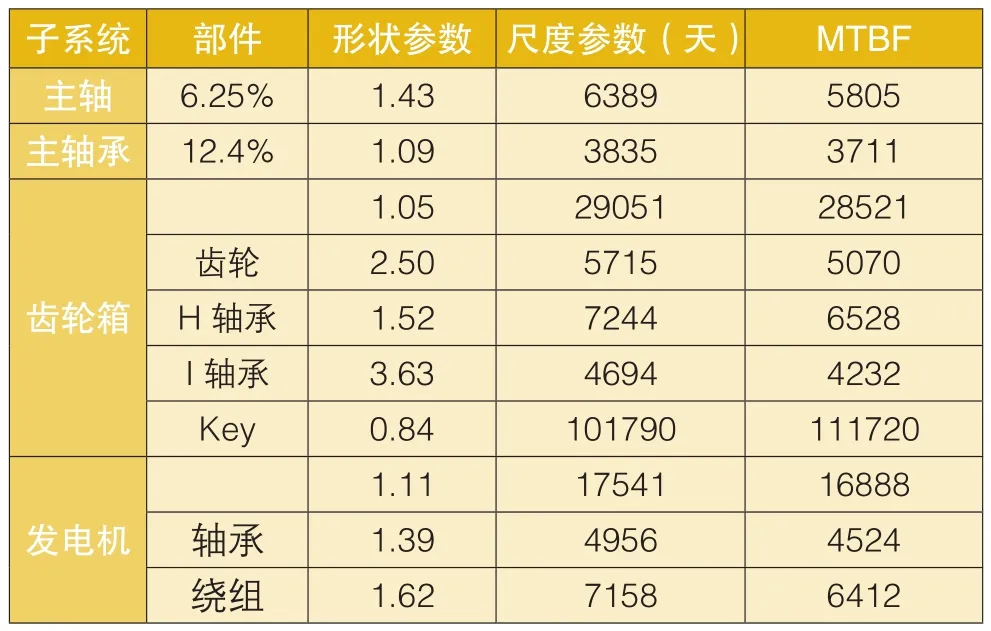
表3 風電機組關鍵部件故障模式分析

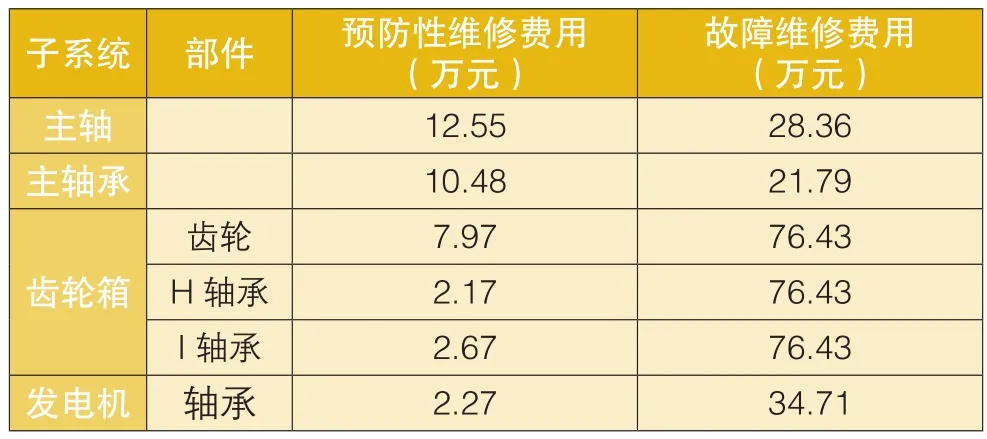
表4 風電機組關鍵部件維修費用

表5 風電機組關鍵部件平均維修/故障費用（元/天）

結語

居高不下的風電機組維護費用增加了風電場的運營費用。本文針對風電機組關鍵部件建立了可靠性分析模型、維修費用模型和定期更換模型。通過仿真計算，確定了關鍵部件的維護策略，給出了相關部件的最優更換間隔期。采用優化后的維護策略可以大大降低機組的平均維修/故障費用。

（作者單位：翟長武：張家口供電公司下花園客戶服務分中心；董玉亮：華北電力大學能源動力與機械學院）