窄帶通信信號時延估計的循環譜組合切片法

翟曉光，武傳華

(電子工程學院，合肥 230037)

?

窄帶通信信號時延估計的循環譜組合切片法

翟曉光，武傳華

(電子工程學院，合肥 230037)

摘要：循環時延估計方法只使用單一循環頻率進行時延估計，對信號的循環平穩信息利用不充分，且估計性能對循環頻率的選擇有較大依賴性。針對此問題，研究了利用多循環頻率組合進行時延估計的方法，為減小循環譜密度函數估計的計算量并提高時延估計的精度，闡述了利用循環譜切片組合進行時延估計的方法，在不同信噪比的高斯噪聲和同頻干擾條件下分別進行了仿真實驗。仿真結果表明，多循環頻率時延估計法較單循環頻率時延估計法有更高的估計性能。

關鍵詞：循環平穩；通信信號；時延估計；到達時差

0引言

無源時差定位系統具有精度高、隱蔽性強、對天線要求低等特點，在通信對抗偵察中有著廣泛的應用。在時差定位系統中，最后的目標定位精度很大程度上取決于時延估計的精度,因此研究快速、準確的時延估計方法一直是電子對抗信號處理領域的熱點。常規的時延估計算法，通常將信號建模為平穩隨機信號，實際上通信信號由于自身的調制特性，大多具有周期平穩的特點，更適合被建模為循環平穩信號[1]。基于循環平穩信號的時延估計算法能夠適應強噪聲信號環境，具有抗同頻干擾能力，有助于提高時延估計的精度[2]。文獻[3]對幾種循環時延估計方法進行了分析，并論證了其間的相互關系。但幾種方法都存在著本質上的缺陷，即都只用了單一循環頻率進行時延估計，沒有充分利用信號的循環平穩特性。此外，利用循環時延估計法進行時延估計前，往往需要在整個(f,α)平面上進行二維運算，估計出完整的循環譜密度函數，計算量較大，不利于工程實現。

針對上述問題，本文提出了以下改進：考慮到通信信號的循環頻率通常不唯一，在信號的多個循環頻率上進行時延估計并適當融合，提高時延估計的精度和穩健性。考慮到循環自相關函數和循環譜密度函數具有相同的循環頻率集，從自相關函數的循環頻率軸上提取出感興趣的峰值循環頻率，在這些特定的循環頻率上分別計算循環譜密度切片，利用切片組合進行時延估計。

1循環時延估計方法

1.1循環時延估計的數學模型

限于篇幅，下面僅對循環時延估計方法中的循環譜相關法進行簡要介紹，其余時延估計方法可參考文獻[3]。考慮用2個接收機對1個通信電臺進行時差定位，則時延估計的信號模型可以表示為：

x(t)=s(t)+n1(t)

(1)

y(t)=As(t-D)+n2(t)

(2)

式中：x(t)和y(t)為2個接收機接收到的信號；s(t)為關注的信號(SOI)；n1(t)和n2(t)為獨立噪聲；A為信號的相對幅度衰減；D為兩接收機接收SOI的時間不同而引起的相對時差。

假定SOI與噪聲均為零均值且統計獨立。大部分通信信號都具有循環平穩性，即其統計特征值是時間的周期函數。可定義兩接收信號的循環自(互)相關函數如下[4]：

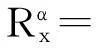
(3)

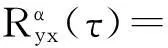
(4)

式中： α為SOI的循環頻率，一般與信號的載頻及碼元速率等參數有關；<·>表示時間平均；*表示共軛運算。

(5)

(6)

對式(5)和式(6)分別做傅里葉變換即可得到信號的循環自譜密度函數和循環互譜密度函數：

(7)

(8)

式(7)和式(8)說明，信號的二階循環統計量可以有效抑制噪聲的影響，并且完整保留SOI的時延信息。時差估計的循環譜相關法可表示為：

(9)

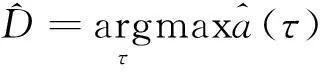
(10)

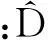
1.2多循環頻率循環時延估計

文獻[5]詳細推導了單循環頻率循環時延估計方法的估計精度：

(11)

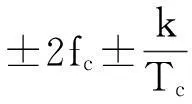
2循環譜密度組合切片法

如前文所述，運用循環譜相關法進行時延估計時需要得到信號的循環譜密度函數。工程上常用的循環譜密度估計方法分為時域平滑周期圖法和頻域平滑周期圖法2種。2種方法的計算量較大，不利于工程實現。雖然也有各種快速算法(數字化頻域平滑算法(DFSM)、分段譜平均算法(SSCA)等)的提出[7]，但仍不能滿足對信號進行實時處理的要求。參考文獻[8]和文獻[9]的思路，現考慮不計算出全部循環譜密度函數，而只是計算需要的循環譜密度在特定循環頻率的截面，以減小計算量。

循環平穩信號的非線性變換是周期性平穩的，可以從中產生出有限強度的正弦波，但信號本身并不含任何有限強度的加性正弦波分量。產生一個正弦波所需用的非線性變換的最小階數稱為信號的循環平穩階數。將信號x(t)的時變自相關函數定義為：

Rx(t,τ)=E{x(t)x*(t-τ)}

(12)

假設信號x(t)為二階循環平穩，即其時變自相關函數具有周期為T0的周期性，則也可用時間平均將Rx(t,τ)寫為：

(13)

由于周期函數可以展開為傅里葉級數，故可得到：

(14)

(15)

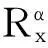
(16)

即令循環自相關函數不為零的頻率集合。

感冒是這個季節寶寶最常見的上呼吸道疾病，中醫講究風寒風熱，中醫辨證論治首先要區分寒證與熱證，我們可以根據“發熱”和“怕冷”輕重來判斷寒熱：簡單的說“怕冷”大于“發熱”的是“風寒”，反之便是“風熱”。

經研究表明，循環譜密度函數和循環自相關函數在循環頻率軸上具有相同的循環頻率集。因此，可由信號的時變自相關函數在某一固定時延τ下以t為變量做傅里葉變換，即可得到循環自相關函數，而通過循環自相關函數可以得到信號循環譜密度函數的循環頻率集，并從中選取感興趣的循環頻率，求特定α截面上的循環譜密度函數切片。

求得循環頻率集后，特定α截面上的循環譜密度切片可由DFSM算法快速計算。循環譜密度函數僅在循環頻率處取值，在非循環頻率處值為零，因此循環譜密度切片保留了信號時延的全部信息，且相比于由測量信號直接進行估計，此方法將循環平面上二維計算簡化為特定循環頻率處的幾個一維計算，顯然計算量大大減小。

3仿真分析

3.1循環譜組合切片法

以下對循環譜組合切片法進行仿真說明。仿真對象為BPSK信號。信號載頻1 MHz,碼元速率1×104Hz，首先對其進行時延為定值的循環自相關切片分析，如圖1所示。

圖1　循環自相關函數

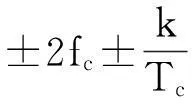
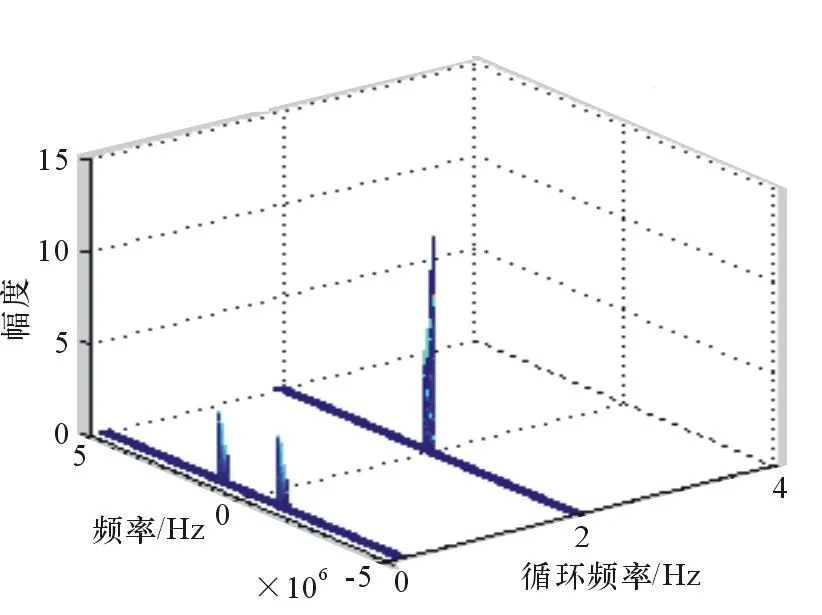
圖2　循環譜密度組合切片

3.2多循環頻率組合時延估計

圖3給出了不同信噪比條件下，多循環頻率時延估計和單循環頻率時延估計的性能比較。圖3中，三循環頻率時延估計法的性能要優于雙循環頻率時延估計法，而雙循環頻率時延估計法的性能優于單循環頻率時延估計。仿真實驗結果驗證了前文的分析。

為檢驗不同強度的同頻干擾下，多循環頻率時延估計的性能，進行以下仿真實驗。SOI仍為BPSK信號，信噪比固定為10 dB，且參數及時延設置與前一實驗相同。設干擾信號為調幅信號，載頻為3 MHz，調制信號源為[0,1]之間均勻分布的隨機變量，信噪比固定為10 dB。

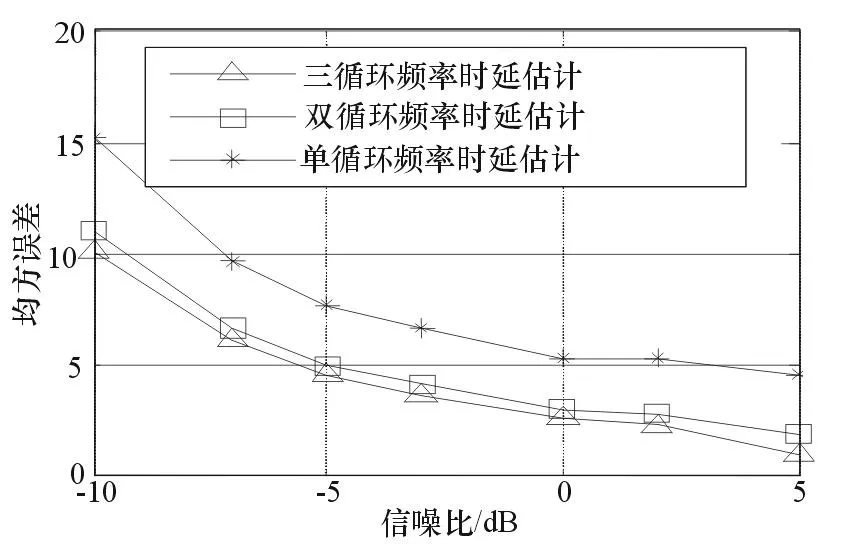
圖3　不同信噪比下多循環頻率時延估計與　　單循環頻率時延估計性能比較

圖4給出了同頻干擾下，多循環頻率時延估計和單循環頻率時延估計的性能比較，橫坐標為SOI與干擾信號之比。從仿真結果可看出，單循環頻率時延估計對同頻干擾較為敏感，估計精度較低，而多循環頻率時延估計在同樣強度的同頻干擾下能取得更高的估計精度，且三循環頻率時延估計法比雙循環頻率時延估計法有更高的精度。仿真表明，多循環頻率時延估計比單循環頻率時延估計有著更好的干擾信號抑制能力。

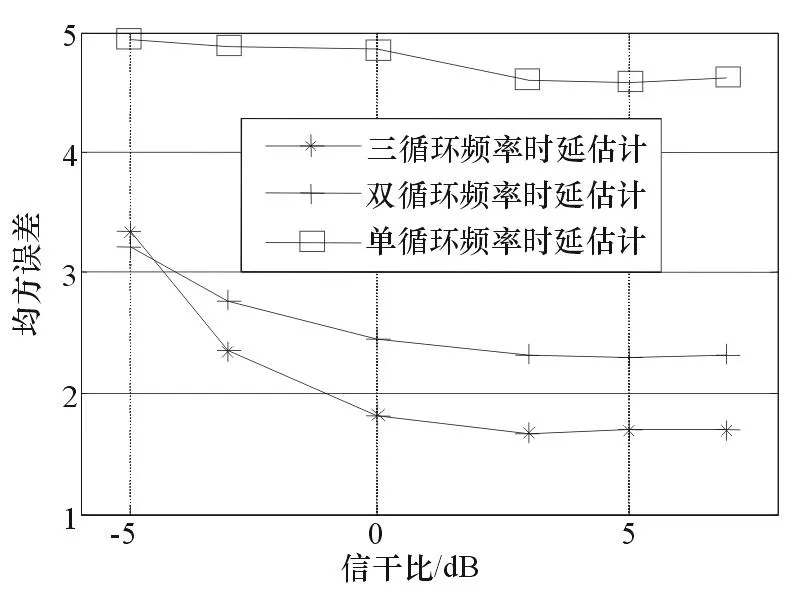
圖4　同頻干擾下多循環頻率時延估計與　　單循環頻率時延估計性能比較

4結束語

針對循環時延估計法只利用了信號單一循環頻率，循環信息利用不充分的問題，研究了多循環頻率組合時延估計方法。同時，考慮到循環譜估計的復雜度，提出了循環譜密度組合切片分析的方法，可針對性地提取特定循環頻率上的信號時延信息，而不必對整個循環譜進行估計，有效減少了計算量。仿真結果表明，在高斯噪聲背景下，多循環頻率時延估計算法比單循環頻率時延估計算法有著更高的精度；而在同頻干擾條件下，多循環頻率時延估計算法比單循環頻率時延估計算法有著更好的穩健性。

參考文獻

[1]王宏禹，邱天爽，陳喆.非平穩隨機信號分析與處理[M].2版.北京：國防工業出版社，2008:206-212.

[2]王江，楊景曙.一種多信號環境下的時差估計方法[J].現代雷達，2007,29(9):84-86.

[3]劉洋，邱天爽，畢峰.循環時延估計方法相互關系研究[J].大連理工大學學報，2012，52(4):589-593.

[4]黃知濤，周一宇，姜文利.循環平穩信號處理與應用[M].北京：科學出版社，2006:104-109.

[5]黃知濤，姜文利，周一宇.多循環頻率循環時延估計方法及性能分析[J].電子學報，2004,32(1):102-108.

[6]黃知濤，周一宇，姜文利.循環相關匹配濾波器設計[J].電子學報，2002,30(12):122-126.

[7]GARDEN William A.Measurement of spectral correlation[J].IEEE Transactions on ASSP,1986,34(5):1111-1123.

[8]陳志敏，朱海潮，毛榮富，杜向華.循環譜密度組合切片分析在近場聲全息中的應用研究[J].聲學學報，2012,37(2):164-169.

[9]陳志敏，朱海潮，毛榮富.循環平穩聲場的聲源定位研究[J]．物理學報，2011,60(10):442-448.

[10]王洪.譜相關的數學關系與物理意義[J].電子學報，2015,43(4):810-815.

Cyclic Spectral Combination Slice Method Based on Time Delay Estimation of Narrow-band Communication Signal

ZHAI Xiao-guang,WU Chuan-hua

(Electronic Engineering Institute，Hefei 230037，China)

Abstract:Cyclic time delay estimation (TDE) method only uses single cyclic frequency to estimate the time delay,which can not make full use of cyclostationary information of signals,and the estimation performance relies on the choices of cyclic frequency very much.To solve this problem,this paper studies the method that uses multi-cyclic frequency combination to estimate the time delay,to decrease the calculating quantity of cyclic spectral density (CSD) function estimation and improve the TDE precision,expatiates the method that uses cyclic spectral slice combination to estimate the time delay,performs simulation experiments under the conditions of Gaussian noise with different signal to noise ratio (SNR) and same frequency interference.Simulation results show that the estimation performance of multi-cyclic frequency TDE method is better than that of single-cyclic frequency TDE method.

Key words:cyclostationary;communication signal;time delay estimation;time difference of arrival

收稿日期:2015-09-02

中圖分類號：TN975

文獻標識碼：A

文章編號：CN32-1413(2016)02-00026-04

DOI:10.16426/j.cnki.jcdzdk.2016.02.007