軟容量約束的物流設施選址問題的改進差分進化算法
張新邦++邢航++李貴棟++汪恭書


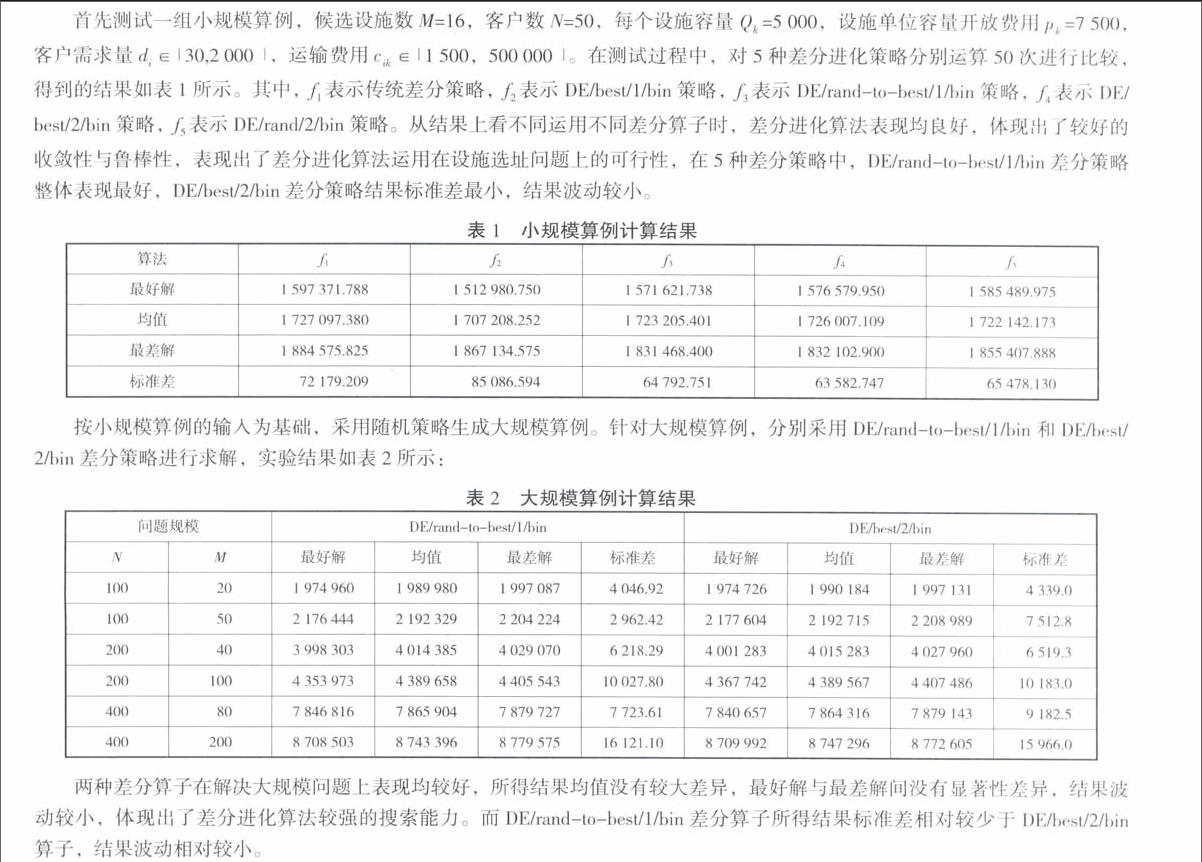
摘 要:研究了廣泛存在于物流系統設計與管理中的軟容量約束的物流設施選址問題,主要決策每個客戶需求由哪個設施服務以及每個設施開放的次數,目標為最小化設施開放成本和運輸成本之和。為了有效求解該問題,提出了一種改進的差分進化算法,編碼方式上采用實數編碼策略,較為簡單易于實現且能得到較好結果,進化過程采用多種變異算子并進行對比。對以往文獻給出的算例采用5種變異算子進行測試,計算結果表明,DE/rand-to-best/1/bin變異算子最好,且所有算子都能得到較好結果,DE算法在軟容量約束的設施選址問題上應用具有可行性。
關鍵詞:物流設施選址問題;軟容量約束;差分進化;實數編碼
中圖分類號:F253.9 文獻標識碼:A
Abstract: This paper studies the soft-capacitated logistics facility location problem that is widely existed in the design and management of logistics system. The problem is to make decision that each customer demand should be serviced by which facility and the open times for each facility so as to minimize the sum of facility opening cost and transportation cost. To solve the problem efficiently, we proposed an improved differential evaluation algorithm. The proposed algorithm uses a real number coding strategy to implement easily, and compares multiple mutation operators in the evolutionary process. We test 5 mutation operators over the instances collected from an existing article. The computational results show that the DE/rand-to-best/1/bin has the best mutation operator, and all other mutation operators can also get better solution for some instances. This verifies that it is feasible to use differential evaluation algorithm to solve the soft-capacitated logistics facility location problem.
Key words: logistics facility location problem; soft-capacitated; differential evaluation; real number coding
0 引 言
設施選址問題是物流與供應鏈管理領域一類重要的組合優化問題,其在企業選址、網絡設施及服務點的分布等眾多方面都有應用。自1909年韋伯發表了關于設施選址問題的第一篇論文至今,該類問題備受眾多研究者青睞。這一問題受到廣泛關注是因為對設施選址問題的研究存在著極為重要的實際意義。選址決策屬于長期的,具有戰略意義的決策,決策的好壞對于服務方式、服務質量、生產成本等方面都有很大的影響,通常一個較好的設施選址方案會很大程度減少不必要的費用,對一個企業而言,甚至還會極大、長久地影響到其生產經營、市場競爭力甚至企業的發展命運。從宏觀而言,設施選址影響著經濟、政治、文化、社會、生態各個方面,以及系統的運行效率。
設施選址問題常被分為有容量約束的設施選址問題(Capacitated Facility Location Problem)、無容量約束的設施選址問題(Un-capacitated Facility Location Problem)和軟容量約束的設施選址問題(Soft-capacitated Facility Location Problem)。目前對設施選址問題的研究已有一些不錯的研究成果。如Guha & Khuller[1]將一維的無容量限制的設施選址問題推廣至k維,并通過實驗得到1.463的硬度近似比;Jain et al[2]的研究表明貪婪算法可以用于求解帶懲罰的無容量約束設施選址問題且近似比為2;Charikar & Guha[3]將原始對偶方法與增強的貪心算法相結合得到近似比為1.853。
本文主要研究了軟容量約束的設施選址問題。軟容量指的是在考慮設施提供服務的有限性的同時,考慮到現實生活中設施可以多次開設并支付費用來增加自身容量。該類問題的目標是使設施開設費用和連接費用之和的最小。對于此類問題,Arya et al[4]提出了一種局部搜索算法,得到了一個近似比為3.72的優化結果;Jain et al[5]的研究表明軟容量近似比可以達到3。徐大川等[6]研究兩階段模型,考慮隨機性與容錯率,使用原始—對偶近似算法進行求解。Holmberg et al[7]針對有容量約束的設施選址問題,提出了最優化精確算法,可求得中小規模問題的最優解。
從目前的研究情況來看,運用近似算法來求解該類問題,雖然步驟簡潔和計算復雜度低,但其優化結果較最優解還有較大距離。運用最優化算法來進行求解,雖然能得到最優解,但從最優化算法自身的特點來看,其無法解決大規模問題。目前有一種備受學術界關注的優化算法—智能優化算法,其能夠在短時間內獲得高質量解的優化算法,能從一定程度上彌補以上兩種算法在求解該類問題時的缺點,且其不受問題結構的限制,是一種優化問題的較好選擇。本文正是嘗試運用目前一種較好的智能優化算法—差分進化算法來求解軟容量約束的設施選址問題。endprint
差分進化算法是1995年Storn和Price提出的一種仿生物進化的智能優化算法[8],近年由于其較好的魯棒性與收斂性得到越來越多學者的關注。應用DE求解設施選址問題關鍵是對編碼方法、變異和交叉過程等進行合理設計,使其得到較為理想的結果。
本文針對軟容量約束的設施選址問題的特點,對差分進化算法編碼、變異以及交叉過程進行設計,編碼過程采用實數編碼策略,改進了差分算子,并且對不同差分算子進行了比較,選擇過程采用貪婪策略。通過實驗可以看出,本文應用差分進化算法解決該類問題具有可行性。
4 結 論
本文研究了一類廣泛存在于物流系統設計與管理中的軟容量約束條件下的設施選址問題,建立了問題的混合整數規劃模型,提出了收斂速度與魯棒性較好的差分進化算法的求解方法,并通過實驗對比了不同變異算子作用下的結果,驗證了差分進化算法在此類問題上的可行性。
參考文獻:
[1] Guha S, Khuller S. Greedy Strikes Back: Improved Facility Location Algorithms[J]. Journal of Algorithms, 1999,31(1):228-248.
[2] Jain K, Mahdian M, Markakis E, et al. Greedy Facility Location Algorithms Analyzed using Dual Fitting with Factor-Revealing LP[J]. Journal of the Acm, 2002,50(6):127-137.
[3] Charikar M, Guha S. Improved Combinatorial Algorithms for Facility Location Problems[J]. Foundations of Computer Science Annual Symposium on, 1999,34(4):378-388.
[4] Arya V, Garg N, Khandekar R, et al. Local Search Heuristics for k-median and Facility Location Problems[J]. Siam Journal on Computing, 2004,33(3):21-29.
[5] Jain K, Mahdian M, Saberi A. A New Greedy Approach for Facility Location Problems[C] // Proceedings of Annual Acm Symposium on the Theory of Computing, 2010:731-740.
[6] 徐大川,萬瑋,吳晨晨,等. 隨機容錯設施選址問題的原始—對偶近似算法[J]. 運籌學學報,2014,18(2):17-28.
[7] Holmberg K, Ronnqvist M, Yuan D. An exact algorithm for the capacitated facility location problems with single sourcing[J]. European Journal of Operational Research, 1999,113:544-559.
[8] Storn R, Price K V. Differential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces[J]. Journal of Global Optimization, 1995,23(4):341-359.endprint

