基于反演法的某制導迫彈魯棒自適應控制器設計

廖海波

(安徽神劍科技股份有限公司，合肥　230601)

?

基于反演法的某制導迫彈魯棒自適應控制器設計

廖海波

(安徽神劍科技股份有限公司，合肥230601)

摘要：設計了一種基于反演法的魯棒自適應控制器，以解決制導迫彈在飛行中存在的氣動參數不確定和未建模誤差等問題，在設計過程中通過帶有σ修正的參數自適應律對系統中的不確定參數進行在線估計，針對模型中的未建模誤差，采用魯棒函數抵消，在反演法的推導過程中，加入了一階低通濾波器，得到虛擬控制量的微分，消除了傳統反演法中的“項數膨脹”難題，并利用李雅普諾夫函數證明了該閉環系統為半全局穩定的。該設計方法放寬了對不確定項的限制，仿真結果證明了該方法的有效性。

關鍵詞:制導迫彈;反演法;自適應控制；魯棒控制

制導迫彈是當前國家重點發展的對象，能夠為營級部隊提供可靠的火力支援。制導迫彈借助于常規迫榴炮發射平臺發射，通過制導控制系統引導迫彈命中目標[1]。制導迫彈外界環境干擾較為復雜，并且其運動模型是一個非線性、多變量的系統，因此模型中存在較大誤差，主要集中在氣動參數誤差和未建模動態。系統中不確定性會嚴重影響整個系統的性能，采用傳統的線性控制理論難以取得較好的控制效果，應尋找更為有效的非線性控制設計方法[2]。

反演法在20世紀90年代被提出，它能夠有效處理系統的不確定性和未知參數，其思想為結合李雅普諾夫函數逐層設計虛擬控制變量，并一直“后退”到整個系統，直到完成全部控制律的設計[3-4]。它能夠避免對消系統中有用的非線性，以鎮定和跟蹤為其追求的目標。但是在推導過程中，會導致“項數膨脹”,使控制器難以工程實現。為解決“項數膨脹”問題,文獻[5]中提出了動態面控制方法，在設計過程中引入一階低通濾波器，降低了控制律的復雜度，解決了該難題。國外學者在文獻[5]中的基礎上，將魯棒自適應與反演法相結合，為多種飛行器設計了控制器，文獻[6]基于動態面為小靈巧炸彈設計了反演控制器，但當系統存在氣動參數不確定性及未建模動態時，控制器效果較差，文獻[7]中將反演法與滑膜控制結合為BTT導彈設計了自適應控制器，有效地補償了系統不確定性的影響，但該方法要求較為苛刻，要求系統不確定性已知。

本研究將魯棒、自適應、反演法相結合，為帶有不確定性的制導迫彈模型設計了一種魯棒自適應控制器。引入了一類魯棒函數來補償系統的建模誤差，并通過自適應律對不確定上界進行估計，通過低通濾波器克服“項數膨脹”的難題，針對氣動參數的不確定性，采用自適應律對其進行在線估計，有效地利用了已知信息。

1模型建立

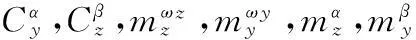
(1)

式中

xi=(x1,x2,x3,x4)=(α,β,ωz,ωy)

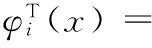
2魯棒自適應控制律設計

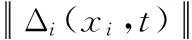
1)俯仰通道控制系統設計

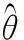
(2)

(3)

對S1求導可得

(4)

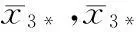
(5)

濾波器輸出誤差如式(6)所示

(6)

(7)

由此式(4)可以改寫為

(8)

該控制系統的誤差項有4部分組成，迫彈攻角和目標攻角的跟蹤誤差，濾波器輸出誤差，氣動參數估計誤差以及系統未建模誤差，如果上述4個誤差均能限制在較小范圍內，則該控制系統是穩定且能夠跟蹤指定目標。選定李雅普諾夫函數V1并對其求導。

(9)

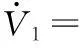
(10)

針對上述公式需進行部分簡化，k1=2+Γ又由Young’s不等式可知

最終式(10)可改寫為

(11)

為了能有效地利用已知信息，改善參數估計的精度。本文采用帶σ修正的傳統參數適應律。

(12)

(13)

(14)

利用

(15)

(16)

最終可推得

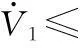
(17)

又由

(18)

最終可以推出

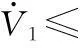
(19)

第二步對定義的第三個動態面求導

(20)

選取控制器的輸入為

(21)

同理取

(22)

對傳統參數適應律進行σ修正。

(23)

(24)

(25)

選取第二個李亞普諾夫函數

(26)

同理可以推出

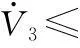
(27)

令 C1=min{2Γ,ο1r1,ο3r3,σ1T1,σ3T3,σ5T5}

可得

(28)

解式(28)可得

(29)

顯然可得

(30)

由式(30)可知

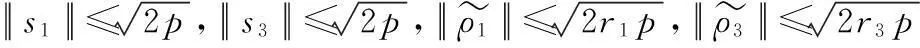
最終可以證明攻角的跟蹤誤差、一階低通濾波器、未建模動態及其參數估計誤差有界且收斂至系統原點的一個領域內。由于引入了自適應律進行在線估計，參數不確定上限已知的限制條件得以放寬。

2)偏航通道控制系統設計

偏航通道設計過程與縱向通道較為類似，同理針對公式 第二項和第四項引入新的變量S2、S4。S2、S4分別為迫彈側滑角和偏航角度率與目標側滑角和目標偏航角度率之間的誤差。參數適應律選取與俯仰通道類似，不再詳細推導，控制器的輸入選取如下：

(31)

針對1的第二項、第四項選取李雅普諾夫函數如下

(32)

令 C1=min{2Γ2,ο2r2,ο4r4,σ2T2,σ4T4,σ6T6}

故可得

(33)

顯然可得

(34)

最終同理可以證明制導迫彈的偏航通道也是穩定的，且系統誤差可以被限制在一個有界的范圍之內。至此可以證明出制導迫彈的俯仰和偏航通道控制器均是穩定的。

通過上述推導可以看出該系統俯仰和偏航通道的控制器輸入是相互耦合的。控制系統輸入如下

(35)

3仿真分析

接下來以某型制導迫彈為例對所設計的控制器進行仿真，假設制導迫彈在某個特征點處速度為270 m/s，滾轉角速度為2 r/s，初始攻角和側滑角為0。系統建模誤差為 E=2×sin(πT)[0.1,0.2,0.3,0.4]T，接下來對上述研究控制器進行仿真，以縱向為例進行說明。

經多次嘗試控制器增益最終取為Γ=1.5,Γ2=2,o1=3,o2=4,o3=4,o4=5σ1=100,σ2=120,σ3=80,σ4=100,σ5=150,σ6=200。

圖1～圖2為制導迫彈跟蹤指定姿態角的仿真圖，由圖1～圖2可知仿真曲線吻合程度較高，能夠準確地跟蹤指定姿態角。圖3為俯仰通道等效舵片角仿真圖。

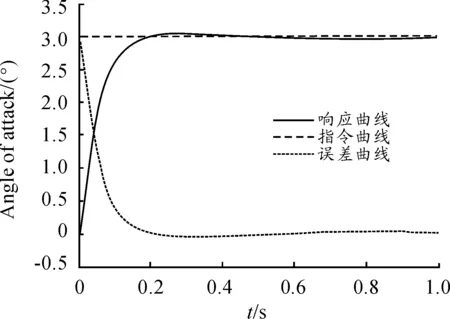
圖1　制導迫彈跟蹤指定攻角

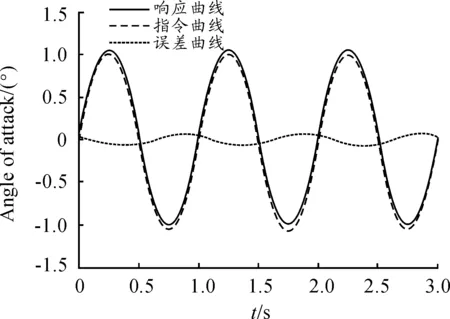
圖2　制導迫彈攻角跟蹤正弦曲線

圖3　俯仰等效舵偏角曲線響應圖

4結束語

反演法的提出，極大地促進了非線性控制的發展，該方法的控制規律能夠提供收斂的穩定的性能，并且能夠保留對系統有益的非線性特性。本文在實際考慮制導迫彈飛行過程中存在氣動參數不確定及未建模誤差的情況下，基于反演法設計了一種魯棒自適應控制律，通過參數自適應律對系統中的不確定參數進行在線估計，采用魯棒函數抵消模型中的未建模誤差，引入一階低通濾波器，消除傳統反演法中的“項數膨脹”難題，李雅普諾夫函數證明了該閉環系統為半全局穩定的，最后基于Matlab/Smulink的仿真驗證了該設計方法的有效性。

參考文獻：

[1]曹小兵,徐伊岑，王中原,等.迫彈橫向脈沖控制飛行穩定性[J].彈道學報,2008,20(4):41-44.

[2]陳圣,王旭剛．制導炮彈非線性魯棒自適應控制系統設計[J]．電光與控制，2014,21(4):61-64.

[3]郭一,劉金琨.飛行器航跡傾角的自適應動態面控制[J].北京航空航天大學學報,2009,39(2):275-279.

[4]董長虹,周國杰,徐世杰.反演法在導彈非線性控制系統設計中的應用[J].航天控制,2010,28(1):3-6.

[5]SWAROOP D,HEDRICK J K,YIP P P,et al.Dynamic surface control for a class of nonlinear systems[J].IEEE Trans Automatic Control,2000,45(10):1893-1899.

[6]張志民.小靈巧炸彈BTT控制器設計與彈道仿真[D].南京:南京理工大學，2010.

[7]ZHOU J W,WEN C.Adaptive Backstepping Control of Uncertain systems[M].Berlin:Spinger-Verlag,2007.

[8]鄭友勝.遠程制導炮彈彈道優化設計與姿態控制方法研究[D].南京:南京理工大學，2008.

[9]錢杏芳.導彈飛行力學[M].北京:北京理工大學出社,2011.

[10]王轔，高原，范文濤.基于反演變結構方法的變外形導彈控制系統[J].探測與控制學報，2014(3)：46-51.

(責任編輯周江川)

本文引用格式：廖海波.基于反演法的某制導迫彈魯棒自適應控制器設計[J].兵器裝備工程學報，2016(5):70-73.

Citation format:LIAO Hai-bo.Guided Mortar Projectile Robust Adaptive Controller Design Based on Backstepping[J].Journal of Ordnance Equipment Engineering,2016(5):70-73.

Guided Mortar Projectile Robust Adaptive Controller Design Based on Backstepping

LIAO Hai-bo

(Anhui Shenjian Technology Company Limited,Hefei 230601,China)

Abstract:A controller using robust adaptive based on backstepping was designed for guided mortar projectile with uncertain aerodynamic parameters and unmodeled dynamics.The problem of uncertain aerodynamic parameters was solved by the parameter estimator through parameter self-adaptive with σ amendatory,and the robust term was designed to solve the problem about approach error．“Explosion of complexity” which existing in traditional backstepping approach was solved by introduction of low pass filters.Finally,the closed-loop system was proved by Lyapunov function for semi-global stability and the research object was expanded to a nonlinear dynamics system.The numerical simulation shows that the proposed control system illustrates good tracking performance and robustness.

Key words:guided mortar projectile; backstepping; adaptive control; robust control

doi:【裝備理論與裝備技術】10.11809/scbgxb2016.05.017

收稿日期：2015-12-08；修回日期：2015-12-29

作者簡介：廖海波(1976—)，男(土家族)，碩士，總工程師，主要從事彈箭總體設計研究。

中圖分類號：TJ765.2

文獻標識碼：A

文章編號：2096-2304(2016)05-0070-05