基于橢球假設的加速度計非正交誤差角測試

翟子雄， 張丕狀

(中北大學 儀器科學與動態測試教育部重點實驗室，山西 太原 030051)

?

基于橢球假設的加速度計非正交誤差角測試

翟子雄， 張丕狀

(中北大學 儀器科學與動態測試教育部重點實驗室，山西 太原 030051)

摘要:針對現有三軸加速度計非正交誤差角測試方法成本高、現場測試能力不足以及對加速度計測試位置精度要求高的問題，提出一種基于橢球假設的現場無依托測試方法。在只考慮三軸加速度計非正交誤差角因素下,建立了三軸加速度計誤差模型。實驗結果表明:采用橢球假設現場測試方法可以不依賴外部輔助設備，通過繪制橢球的圓球程度可以直觀觀察到非正交誤差角對加速度計的影響，同時可以對加速度計非正交誤差角進行補償。

關鍵詞:加速度計； 非正交誤差角； 橢球假設

0引言

三軸MEMS加速度傳感器以其低成本、低功耗、小型化的優勢在航天器、導彈、機器人的姿態測量中已得到廣泛的應用[1～3]。理想情況下，加速度傳感器的3個軸是完全正交的，但其敏感軸通常會偏離正交坐標系微小的角度[4]，從而產生非正交誤差。加速度傳感器的非正交誤差角將影響姿態精度，因此，需要對加速度傳感器進行測試與校正，研究其非正交誤差角對真實加速度的影響，這樣以利于對加速度傳感器的測量值進行補償，提高姿態測試精度。

傳統的加速度傳感器測試需要昂貴的位置姿態測量儀器，如轉臺，測試工作只能在實驗室里進行，不適合非實驗室環境下使用[5]。文獻[6]利用16位置翻轉法對加速度傳感器進行測試，該方法對不同位置時的姿態角精度要求較高，姿態誤差會大大影響加速度傳感器誤差參數的計算精度。

針對傳統測試方法成本高、現場測試能力不足以及對傳感器測試位置精度要求高的問題，本文提出一種基于橢球假設的三軸加速度傳感器測試方法對其非正交誤差角進行測試研究，數據采集時只需要傳感器姿態在三維空間大致均勻分布即可。

1加速度傳感器非正交誤差角模型

當僅考慮加速度傳感器非正交誤差而忽略加速度傳感器的其他誤差時，假設加速度傳感器z軸和正交坐標系的zm軸完全重合，其它兩軸與正交坐標系的夾角分別為α，β，γ，如圖1所示。

非正交誤差可表示為

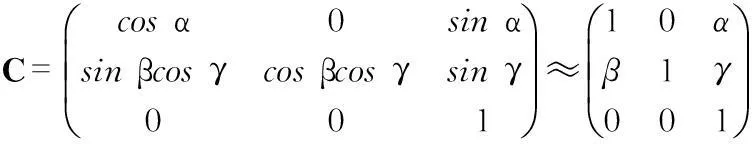
(1)

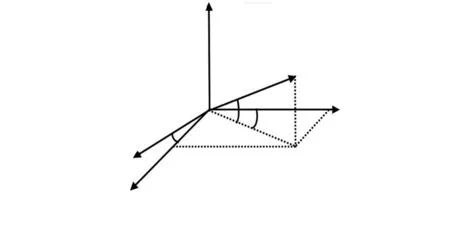
圖1　三軸加速度計非正交誤差角Fig 1　Non-orthogonal error angle of three-axis accelerometer

通常，廠家提供的三軸加速度傳感器非正交誤差角度小于0.5°，因此,可以對式(1)進行化簡。只考慮三軸加速度傳感器的非正交誤差角影響，則真實加速度ge和測量值gm之間的關系如下

ge=L·gm.

(2)

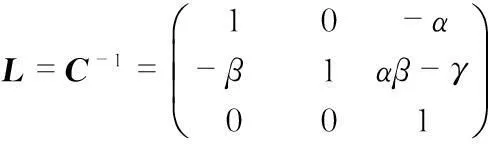
2橢球擬合法

三軸加速度傳感器坐標系O-xbybzb與地理坐標系O-xgygzg關系如圖2所示，重力矢量g垂直向下，θ,φ分別表示載體的俯仰角和滾轉角。某姿態下加速度傳感器的測量值為A=[ax,ay,az]T,重力矢量在加速度傳感器各軸的分量為

Ag=g·[-sinθsinφcosθcosφcosθ]T.

(3)

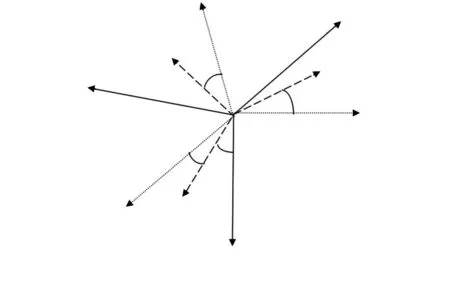
圖2　三軸加速度傳感器坐標系與地理坐標系示意圖Fig 2　Three-axis acceleration sensor coordinate system and geographical coordinate system diagram

在無誤差的理想情況下，測量值A滿足下述方程

AT·A=(1gn)2.

(4)

式中測量值A的軌跡是一個以1 gn為半徑的重力圓球面，實際由于加速度傳感器的三軸存在非正交誤差角，傳感器輸出軌跡會畸變為橢球面。對式(2)取ge模的平方可得

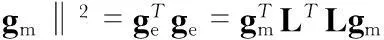
(5)

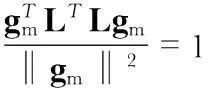
(6)

一般的二次曲面方程可表示為如下形式

ax2+by2+cz2+2fyz+2gxz+2hxy+2px+2qy+2rz+d

=0.

(7)

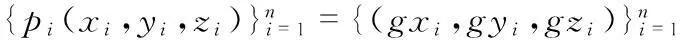
定義

V=[a,b,c,f,g,h,p,q,r,d]T,

(8)

則擬合橢球到測試點的問題可轉化為如下約束問題

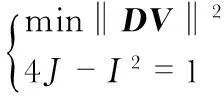
(9)

也可表示為

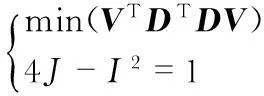
(10)

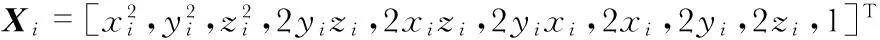
C1=

(11)

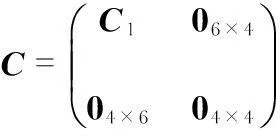
(12)

引入拉格朗日算子，則式(10)可改寫為

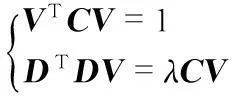
(13)

已經證明上式有唯一解[7],因此,可唯一確定橢球系數向量V。

根據橢球系數可以求出橢球的半軸長度和非正交誤差角。

2.1橢球的半軸長度

在獲得橢球系數后，可定義對稱系數矩陣T與平移向量F[8]

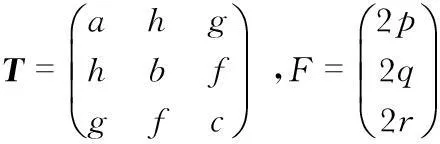
(14)

并構造變換

M′=QTM+R,

(15)

則可將式(7)轉換為標準橢球形式

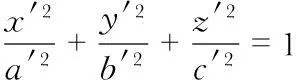
(16)

其中,旋轉矩陣Q為對稱系數矩陣T的特征向量，且Q和向量R滿足

T=QWQT,

(17)

R=-(2W)-1QF,

(18)

式中W為對稱系數矩陣T的特征值構成的主對角陣。

橢球的各半軸長度可得

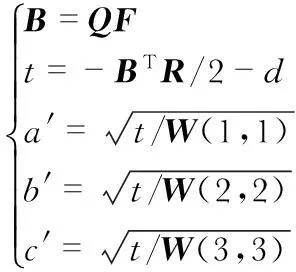
(19)

2.2加速度傳感器的非正交誤差角度

根據橢球系數，利用解析法即可求出非正交誤差角度

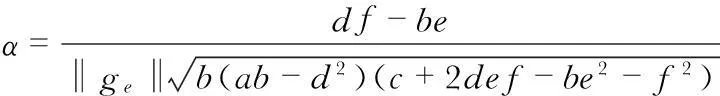
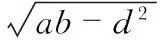
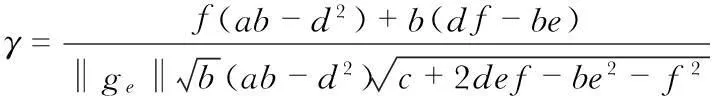
3實驗結果與分析

為了驗證上述橢球假設法對三軸加速度傳感器非正交誤差角的測試效果，將三軸加速度傳感器固定在三自由度轉臺上，根據文獻[9]中的等夾角均勻分布選取20個姿態采集三軸加速度傳感器數據作為測量值。利用橢球擬合法求出半軸長度繪制出的橢球如圖3所示，并求出加速度傳感器非正交誤差角，利用式(2)對加速度傳感器的誤差進行補償，補償結果如圖4所示。

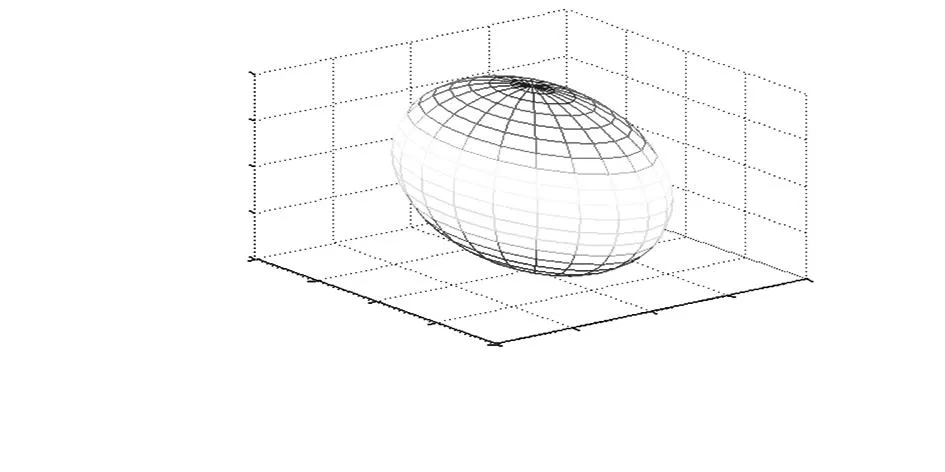
圖3　測量數據橢球曲面Fig 3　Ellipsoid surface of measurement data

通過繪制橢球的圓球程度，可以判斷出三軸加速度傳感器的非正交誤差角對加速度真實值的影響程度。

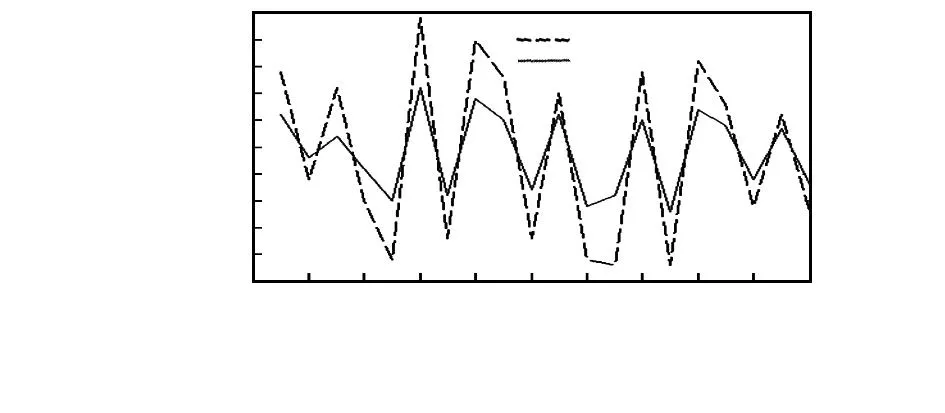
圖4　三軸加速度傳感器20組數據誤差補償Fig 4　Error compensation of 20 groups datas of three-axis accelerometer

圖4中，加速度傳感器最大絕對誤差由校準前的0.472 2m/s2減小到0.211 7m/s2。

4結束語

本文分析了三軸加速度傳感器當只考慮其非正交誤差角時任意姿態下的誤差模型，利用橢球假設法可以求出橢球的半軸長和非正交誤差角，可以通過觀察繪制橢球的圓球程度判斷加速度傳感器非正交誤差角對傳感器的影響程度，同時可以實現對三軸加速度傳感器的非正交誤差的補償。該測試方法可在不需要外界參考基準下現場測試，操作簡單易行。

參考文獻:

[1]李智,汪地,楊浩,等.一種基于三軸加速度傳感器的傾角測量裝置[J].儀表技術與傳感器,2013(8):31-32.

[2]楊淑潔,曾慶雙,伊國興.低成本無人機姿態測量系統研究[J].傳感器與微系統,2012,31(2):15-18.

[3]李杰,洪惠惠,張文棟.MEMS微系統測量組合標定技術研究[J].傳感技術學報,2008,21(7):1169-1173.

[4]陳彎彎,陳智剛,付建平.MEMS微型慣性測量組合標定[J].儀表技術與傳感器,2014(12):37-38.

[5]蔣效雄,劉雨,蘇寶庫.高精度加速度計重力場標定試驗方法[J].吉林大學學報,2010,40(1):287-292.

[6]FangJCH,SunHW,CaoJJ,etal.Anovelcalibrationmethodofmagneticcompassbasedonellipsoidfitting[J].IEEETransactionsonInstrumentationandMeasurement,2011,60(6):2053-2061.

[7]GanderW,GolubGH,StrebelR.Fittingofcirclesandellipsesleastsquaressolution[R].Zurich,Switzerland:ETH，1994:1-57.

[8]LiQ,GriffithsJG.Leastsquaresellipsoidspecificfitting[C]∥2004ProceedingsoftheGeometricModelingandProcessingconf,Beijing,China,2004:335-340.

[9]劉艷霞,李希勝,馮毅博,等.三軸磁羅盤標定位置分布的研究[J].儀器儀表學報,2013,34(3):684-690.

Accelerometer non-orthogonal error angle test based on ellipsoid hypothesis

ZHAI Zi-xiong, ZHANG Pi-zhuang

(Key Laboratory of Instrumentation Science & Dynamic Measurement,Ministry of Education,North University of China，Taiyuan 030051,China)

Abstract:To overcome the problems of high cost,insufficient on-site test ability and high precision demand for accelerometer test location that existing triaxial accelerometer non-orthogonal error angle test method has,a new test method based on ellipsoid hypothesis is proposed for on-site use.Considering only non-orthogonal error angle factors,an error model for triaxial accelerometer is established.Experimental results show that using proposed on-site method based on ellipsoid hypothesis without auxiliary equipment can realize accelerometer non-orthogonal error compensation and the impact of non-orthogonal error angle on accelerometer can be observed visually by the degree of sphere of drawing ellipsoid.

Key words:accelerometer; non-orthogonal error angle; ellipsoid hypothesis

DOI:10.13873/J.1000—9787(2016)03—0151—03

收稿日期：2015—05—20

中圖分類號:V 249

文獻標識碼:A

文章編號:1000—9787(2016)03—0151—03

作者簡介:

翟子雄(1990-)，男，山西太原人，碩士研究生，主要從事慣性導航技術、信號與處理。